Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems
Подождите немного. Документ загружается.

94 Modeling and Control of Vibration in Mechanical Systems
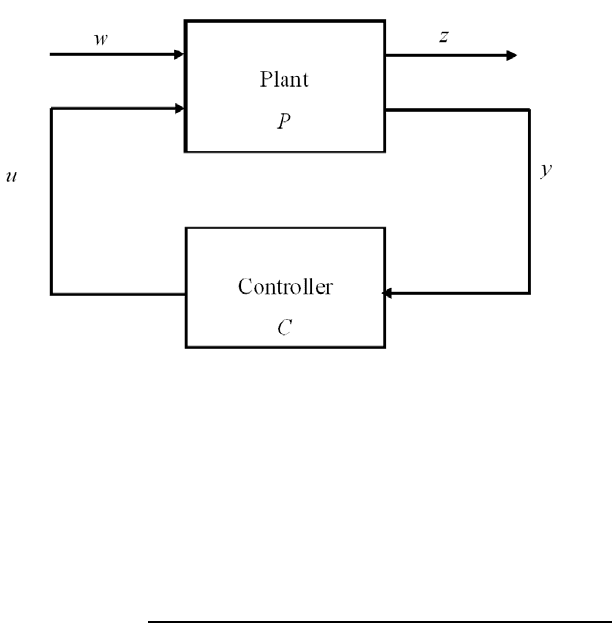
FIGURE 5.1
Configuration of standard optimal control.
where
F = −(D
T
12
D
12
)
−1
(D
T
12
C
1
+ B
T
2
X
2
),
K = −(Y
2
C
T
2
+ B
1
D
T
21
)(D
21
D
T
21
)
−1
. (5.33 )
The minimal H
2
norm of the transfer function T
zw
is given by
kT
zw
k
2
=
q
T race(B
T
1
X
2
B
1
) + T race[(A
T
X
2
+ X
2
A + C
T
1
C
1
)Y
2
].(5.34)
If the conditions (1)−(4) in Assumption 5.1 are not satisfied, the so-called pertur-
bation method is applied [7] so that the above d esign method to find an appropr iate
controller is still appl icable.
5.3.2 Discrete-time case
Consider t he discrete-time linear time-invariant system P (z) with the following state-
space representat ion:
x(k + 1) = Ax(k) + B
1
w(k) + B
2
u(k), (5.35)
z(k) = C
1
x(k) + D
11
w(k) + D
12
u(k), (5.36 )
y(k) = C
2
x(k) + D
21
w(k) + D
22
u(k), (5.37 )
where x ∈ R
n
x
is the state, y ∈ R
n
y
is the measurement output, z ∈ R
n
z
is the
controlled output, w ∈ R
n
w
is the disturbance input, u ∈ R
n
u
is the control input ,
and A, B
1
, B
2
, C
1
, D
11
, D
12
, C
2
, and D
21
are of appropri at e dimensions. D
22
= 0
is also assumed.

Introduction to Optimal an d Robust Control 95
Intr oduce the following dynamic output feedback controller C(z):
x
c
(k + 1) = A
c
x
c
(k) + B
c
y(k), (5.38)
u(k) = C
c
x
c
(k) + D
c
y(k). (5.39 )
Denote ξ = [x
T
x
T
c
]
T
. From (5.35)−(5.37) and (5.38)−(5.39), the closed-loop
system is given by
ξ(k + 1 ) =
¯
Aξ(k) +
¯
Bw(k), (5.40)
z(k) =
¯
Cξ(k) +
¯
Dw(k), (5.41 )
where
¯
A =
A + B
2
D
c
C
2
B
2
C
c
B
c
C
2
A
c
,
¯
B =
B
2
D
c
D
21
+ B
1
B
c
D
21
, (5.42)
¯
C = [C
1
+ D
12
D
c
C
2
D
12
C
c
] ,
¯
D = D
12
D
c
D
21
+ D
11
. (5.43)
The discrete-time H
2
control problem i s to find a proper, real rational cont roller
C(z) that stabilizes P (z) internally and minimi zes the H
2
norm of the transfer func-
tion matrix T
zw
(z) from w to z of the closed-loop system (5.40) −(5.41).
The counterpart of the Riccati equations (5.30)−(5.31) for discrete-time systems
is as foll ows.
A
T
X
2
A −(A
T
X
2
B
2
+ C
T
1
D
12
)(D
T
12
D
12
+ B
T
2
X
2
B
2
)
−1
(A
T
X
2
B
2
+ C
T
1
D
12
)
T
+C
T
1
C
1
= 0, (5.44)
AY
2
A
T
− (AY
2
C
T
2
+ B
1
D
T
21
)(D
21
D
T
21
+ C
2
Y
2
C
T
2
)
−1
(AY
2
C
T
2
+ B
1
D
T
21
)
T
+B
1
B
T
1
= 0 . (5.45 )
A discrete-time H
2
optimal controller can then be obtained as (5.32). And the
minimal H
2
norm of the transfer fun ction T
zw
is given b y
kT
zw
k
2
=
q
T race(B
T
1
X
2
B
1
) + T race[(A
T
X
2
A + C
T
1
C
1
)Y
2
]. (5.46)
A parametrizati on of all H
2
controllers is developed i n terms of LMIs as in the
following theorem which linearizes th e H
2
norm conditions ( 5.14)−(5.15) for syn-
thesis.
THEOREM 5.1
[90] Consider system (5.35)−(5.37). There exists a controller (5.38)−(5.39)
such that k T
zw
k
2
2
< µ if and only if the followi ng linear matrix inequalities
and equali ty admit a solution:
T race(Π) < µ, (5.47 )

96 Modeling and Control of Vibration in Mechanical Systems
Π C
1
X + D
12
E C
1
+ D
12
D
c
C
2
∗ X + X
T
−P
2
I + Z
T
−J
∗ ∗ Y + Y
T
− H
> 0, (5.48 )
P
2
J AX + B
2
E A + B
2
D
c
C
2
B
1
+ B
2
D
c
D
21
∗ H U Y A + W C
2
Y B
1
+ W D
21
∗ ∗ X + X
′
−P
2
I + Z
′
−J 0
∗ ∗ ∗ Y + Y
T
− H 0
∗ ∗ ∗ ∗ I
> 0, (5.49)
and
D
11
+ D
12
D
c
D
21
= 0, (5 .50)
where ∗ denotes an entr y t hat can be deduced from the symmetry of the matrix,
the matrices X, E, Y , W , U, D
c
, Z, J, and the symmet ric matri ces P
2
, H
and Π are the variables. A feasible H
2
controller is obtained by choosing N
1
and M
1
nonsingular such that N
1
M
1
= Z − Y X and calculating
C
c
= (E − D
c
C
2
X)M
−1
1
, D
c
= D
c
, (5.51 )
B
c
= N
−1
1
(W − Y B
2
D
c
), (5.52 )
A
c
= N
−1
1
[U −Y (A + B
2
D
c
C
2
)X − N
1
B
c
C
2
X − Y B
2
C
c
M
1
]M
−1
1
. (5.53)
5.4 H
∞
control
5.4.1 Continuous-time case
We consider the continuous-time system P described b y (5.21)−(5.23), and the class
of causal, linear, time-invariant and finite-dimensional controllers that internally sta-
bilize P , or namely, all admissible controllers for P . Our aim is to find an admissible
controller C such that the closed-loop sy stem T
zw
satisfies
kT
zw
k
∞
< γ. (5.54 )
Assumption 5.2
(1). The pair (A, B
2
) is stabilizable and th e pair (A, C
2
) is detectable.
(2). The matrices D
12
and D
21
satisfy D
T
12
D
12
= I
n
u
and D
21
D
T
21
= I
n
y
.
(3).
rank
A − jωI B
2
C
1
D
12
= n
x
+ n
u
, for all real ω. (5.55)
(4).
rank
A − jωI B
1
C
2
D
21
= n
x
+ n
y
, for all real ω. (5.56 )

Introduction to Optimal an d Robust Control 97
The assumptio n that (A, B
2
, C
2
) is stabilizable and detectable is necessary and
sufficient for the existence of admissible controllers. The full rank assumptions (3)
and (4 ) are necessary for the existence of stabilizing solutions to t he Riccati equations
that are used to obtain the solution to th e H
∞
control problem.
Define the matri ces
ˆ
A,
ˆ
B,
˜
A and
˜
C as
ˆ
A = A − B
1
D
T
21
C
2
,
ˆ
B
ˆ
B
T
= B
1
(I − D
T
21
D
21
)B
T
1
, (5.57)
˜
A = A − B
2
D
T
12
C
1
,
˜
C
T
˜
C = C
T
1
(I − D
12
D
T
12
)C
1
. (5.58)
Suppose that U
y
maps y to u and has a minimal realization (A
u
, B
u
, C
u
, D
u
)
satisfyi ng det(I − D
22
D
u
) 6= 0 for a well-posed closed loop. Then a realization in
terms of LFT is given by
LF T (P, U
y
) =
A + B
2
D
u
MC
2
B
2
(I + D
u
MD
22
)C
u
B
1
+ B
2
D
u
MD
21
B
u
MC
2
A
u
+ B
u
MD
22
C
u
B
u
MD
21
C
1
+ D
12
D
u
MC
2
D
12
(I + D
u
MD
22
)C
u
D
11
+ D
12
D
u
MD
21
, (5.59)
with M = (I − D
22
D
u
)
−1
.
THEOREM 5.2
[71] Consider the system (5.21)−(5.23) satisfying Assumption 5.2. There
exists an admissible C such that the closed-loop system (5.26)−(5.27) satisfies
(5.54) if and only if
1. There is a solution X
∞
≥ 0 t o the algebraic Riccati equation
X
∞
˜
A +
˜
A
T
X
∞
− X
∞
(B
2
B
T
2
− γ
−2
B
1
B
T
1
)X
∞
+
˜
C
T
˜
C = 0, (5.60)
such that
˜
A −(B
2
B
T
2
− γ
−2
B
1
B
T
1
)X
∞
is asymptotically stable.
2. There is a solution Y
∞
≥ 0 to the algebraic Riccati equation
ˆ
AY
∞
+ Y
∞
ˆ
A
T
−Y
∞
(C
T
2
C
2
− γ
−2
C
T
1
C
1
)Y
∞
+
ˆ
B
ˆ
B
T
= 0, (5.61)
such that
ˆ
A −Y
∞
(C
T
2
C
2
−γ
−2
C
T
1
C
1
) is asymptotically s table.
3. ρ(X
∞
Y
∞
) < γ
2
.
In the case when these conditions hold, C i s an admissible controller satis-
fying (5.54) if and only if C is given by the LFT
C = LF T (C
a
, U
y
), kU
y
k
∞
< γ, (5.62)
where U
y
is a stable transfer function. The generator C
a
is given by
C
a
=
A
k
B
k1
B
k2
C
k1
0 I
C
k2
I 0
, (5.63)
98 Modeling and Control of Vibration in Mechanical Systems
where
A
k
= A + γ
−2
B
1
B
T
1
X
∞
− B
2
F
∞
− B
k1
C
2z
, (5.64)
B
k1
B
k2
=
B
1
D
T
21
+ Z
∞
C
T
2z
B
2
+ γ
−2
Z
∞
F
T
∞
, (5.65)
C
k1
C
k2
=
−F
∞
−C
2z
, (5.66 )
C
2z
= C
2
+ γ
−2
D
21
B
T
1
X
∞
, F
∞
= D
T
12
C
1
+ B
T
2
X
∞
, (5.67 )
Z
∞
= Y
∞
(I − γ
−2
X
∞
Y
∞
)
−1
= (I − γ
−2
Y
∞
X
∞
)
−1
Y
∞
. (5.68 )
A point given by Theorem 5.2 is that a solution to the H
∞
generalized regulator
problem exists if and on ly if there exist stabilizing, nonnegative definite solutions
X
∞
and Y
∞
to the algebraic Riccati equations associated with the full information
H
∞
control problem and the H
∞
estimation of C
1
x such that the coupling condition
ρ(X
∞
Y
∞
) < γ
2
is satisfied.
The optimal H
∞
control prob lem is to fin d an i nternally stabil izing controller
C(s) such that kT
zw
k
∞
of the closed-loop system (5.26)−(5.27) is minimized.
However, in practice it is often not necessary to design an optimal controller, and
it is usually appropriate to o btain a controller that gives ri se to an H
∞
norm of the
closed-loo p system less than a prescribed value. More specifically, a suboptimal H
∞
control pro blem is that given γ > 0, find an admissible controller C, if there is any,
such that kT
zw
k
∞
< γ.
The following theorem gives a design method for a suboptimal H
∞
output feed-
back controller.
THEOREM 5.3
[90] Consider system (5.21)−(5.23). Given a scalar γ > 0, there exists an
output feedback controller (5.24)−(5.25) such that kT
zw
k
2
∞
< γ if the following
LMI admits a solution (E, W, U, D
c
, X, Y ):
AX + XA
T
+ B
2
E + (B
2
E)
T
U
T
+ A + B
2
D
c
C
2
∗ A
T
Y + Y A + W C
2
+ (W C
2
)
T
∗ ∗
∗ ∗
,
B
1
+ B
2
W D
c
D
21
(C
1
X + D
12
E)
T
Y B
1
+ W D
21
(C
1
+ D
12
D
c
C
2
)
T
−γI (D
11
+ D
12
D
c
D
21
)
T
∗ −γI
< 0, (5.69)
X I
I Y
> 0 . (5.70)
In this case, a feasible H
∞
controller i s obtained from (5.51)−(5.53), where
N
1
M
1
= I − Y X.
Introduction to Optimal an d Robust Control 99
5.4.2 Discrete-time case
Assume th at the time-invariant discrete-time system (5.35)−(5.37) satisfies:
Assumption 5.3
(1). (A, B
2
, C
2
) is stabilizable and detectable.
(2). D
T
12
D
12
> 0 and D
21
D
T
21
> 0.
(3).
rank
A − e
jθ
I B
2
C
1
D
12
= n
x
+ n
u
, for all θ ∈ (−π, π]. (5.71)
(4).
rank
A −e
jθ
I B
1
C
2
D
21
= n
x
+ n
y
, for all θ ∈ (−π, π]. (5.72)
We seek a causal, linear, t ime-invariant and finite-dimensional controller C(z)
such that the closed-loop system (5.40)−(5.41) is stable and
kT
zw
k
∞
< γ, (5.73 )
or equivalently, under zero initial conditions,
kzk
2
2
− γ
2
kwk
2
2
≤ −εkwk
2
2
, (5.74)
for all w ∈ ℓ
2
[0, ∞) and some ε > 0.
Let
B =
B
1
B
2
, C
d
=
C
1
0
, (5.75 )
D
d
=
D
11
D
12
I
n
w
0
, (5.76 )
J
s
=
I
n
z
0
0 −γ
2
I
n
w
, (5.77)
J
t
=
I
n
w
0
0 −γ
2
I
n
u
. (5.78)
With the assumptions (1)−(4), a causal, linear, finite-dimensional stabil izing con-
troller that leads to kT
zw
k
∞
< γ exists if and only if the following two conditions
hold [71].
1. There exists a solution to the Riccati equation
X
∞
= C
T
d
J
s
C
d
+ A
T
X
∞
A − W
T
R
−1
W, (5.79 )
with
R =
R
1
R
T
2
R
2
R
3
= D
T
d
J
s
D
d
+ B
T
X
∞
B, (5.80 )
W =
W
11
W
21
= D
T
d
J
s
C
d
+ B
T
X
∞
A, W
21
∈ R
n
u
×n
x
, (5.81)

100 Modeling and Control of Vibratio n in Mechanical Systems
such that A − BR
−1
W is asymptotically stable and
X
∞
≥ 0 , (5.82 )
R
1
−R
T
2
R
−1
3
R
2
< 0, R
1
∈ R
n
w
×n
w
, R
3
∈ R
n
u
×n
u
. (5.83)
Denote
∇ = R
1
− R
T
2
R
−1
3
R
2
, W
∇
= W
11
− R
T
2
R
−1
3
W
21
, (5.84 )
and let E
1
be an n
u
×n
u
matrix such that
E
T
1
E
1
= R
3
, (5.85 )
and E
2
be an n
w
× n
w
matrix such that
E
T
2
E
2
= −γ
−2
(R
1
−R
T
2
R
−1
3
R
2
) = −γ
−2
∇. (5.86)
Define the syst em
A
t
B
t
C
t
D
t
=
A −B
1
∇
−1
W
∇
B
1
E
−1
2
0
E
1
R
−1
3
(W − R
2
∇
−1
W
∇
) E
1
R
−1
3
R
2
E
−1
2
I
C
2
− D
21
∇
−1
W
∇
D
21
E
−1
2
0
. (5.87)
2. There exists a solution to the Riccati equation
Y
∞
= B
t
J
t
B
T
t
+ A
t
Y
∞
A
T
t
−M
t
S
−1
t
M
T
t
, (5.88 )
where
S
t
= D
t
J
t
D
T
t
+ C
t
Y
∞
C
T
t
=
S
1
S
2
S
T
2
S
3
, (5. 89)
M
t
= B
t
J
t
D
T
t
+ A
t
Y
∞
C
T
t
=
M
t1
M
t2
, (5.90 )
such that A
t
− M
t
S
−1
t
C
t
is asymptotically stable and
Y
∞
≥ 0, (5.91 )
S
1
−S
2
S
−1
3
S
T
2
< 0. (5.92 )
Note that C
t
in (5.87) is p artitioned as
C
t
=
C
t1
C
t2
=
E
1
R
−1
3
(W − R
2
∇
−1
W
∇
)
C
2
− D
21
∇
−1
W
∇
. (5. 93)
A contro ller that achieves the objective (5.73) is given by
x
c
(k + 1) = A
t
x
c
(k) + B
2
u(k) + M
t2
S
−1
3
(y(k) − C
t2
x
c
(k)), (5.9 4)
E
1
u(k) = −C
t1
x
c
(k)1 − S
2
S
−1
3
(y(k) − C
t2
x
c
(k)). (5.95)

Introduction to Optimal an d Robust Control 101
All controllers that achieve the obj ective (5.73) are generated by the LFT C =
LF T (C
a
, U
c
), where U
c
is a l inear causal system such that kU
c
k
∞
< γ , and the
generator C
a
is given b y
I − B
2
−M
t2
(X
T
2
)
−1
0 E
1
S
2
(X
T
2
)
−1
0 0 X
2
x
c
(k + 1)
u
(
k)
η(k)
=
A
t
0 (M
t1
−M
t2
S
−1
3
S
2
)(γ
2
X
T
1
)
−1
−C
t1
0 X
1
−C
t2
I 0
x
c
(k)
y(k)
φ(k)
, (5.96 )
with
X
2
X
T
2
= S
3
, (5.97 )
X
1
X
T
1
= −γ
−2
(S
1
− S
2
S
−1
3
S
T
2
). (5. 98)
The following theorem g ives one parametrization approach of all suboptimal discrete-
time H
∞
output feedback controllers.
THEOREM 5.4
[90] Consider system (5.35)−(5.37). Given a scalar γ > 0, there exists an
output feedback controller (5.38)−(5.39) such that kT
zw
k
2
∞
< γ if the following
LMI admits a solution:
P
∞
J AX + B
2
E A + B
2
D
c
C
2
B
1
+ B
2
D
c
D
21
0
∗ H U Y A + V C
2
Y B
1
+ V D
21
0
∗ ∗ X + X
′
−P
∞
I + Z
′
− J 0 X
T
C
T
1
+ E
T
D
T
12
∗ ∗ ∗ Y + Y
T
−H 0 C
T
1
+ C
T
2
D
T
c
D
T
12
∗ ∗ ∗ ∗ I D
T
11
+ D
T
21
D
T
c
D
T
12
∗ ∗ ∗ ∗ ∗ γI
> 0, (5.99)
where the matrices X, E, Y , V , U, D
c
, Z, J, and the symmetric matrices P
∞
and H are t he variables. A feasible H
∞
controller is obtained from (5. 51)-
(5.53).
5.5 Robust control
The H
∞
norm is used to test robust stability of a nominally stable system under
unstructured pertu rbations. The fo llowing so-called small gain t heorem is the basis
for robust stability analysis.
102 Modeling and Control of Vibratio n in Mechanical Systems
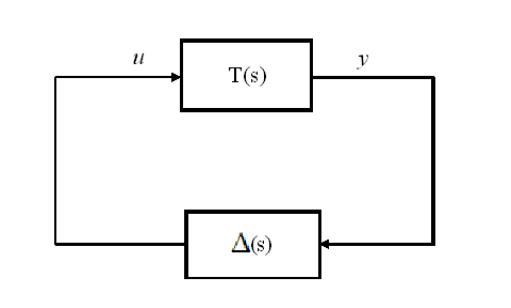
THEOREM 5.5
Smal l Gain Theorem Consider a proper and stable transfer function matrix
T (s). Suppose that a stabl e ∆(s) is connected from the output of T (s) to the
input of T (s) as shown in Figure 5.2. Then the closed-loop system given in
Figure 5.2 is internally stable if
¯σ[∆(jω)]¯σ[T (jω)] < 1, ∀ω ∈ R
[
∞. (5.100)
FIGURE 5.2
A closed-loop system wit h uncertainty.
The small gain condition is sufficient to guarantee internal stabilit y of the closed-
loop system even if ∆ is nonlinear and time-varying. The small gain theorem tells us
that an H
∞
norm bound on T implies closed-loop stability in the presence of certain
H
∞
norm bounded system uncertainties. The H
∞
norm bound implies a certain
stabil ity robustness. Note from (5.100) that the size of tolerable uncertainty vari es
inversely proportional to th e H
∞
norm bo und of T , which means that the robustness
increases as the H
∞
norm bound decreases.
In what follows, the small gain theorem will be used to test robust stability under
model uncertainties. The modeling error ∆ is assumed to be stable and suitably
scaled with weigh ting functions W
1
and W
2
, i.e., the uncertainty can b e represented
as W
1
∆W
2
.
Additive uncertainty
We assume that the model uncertainty can be represented by an additive p erturba-
tion:
Π = P + W
1
∆W
2
, (5.101)
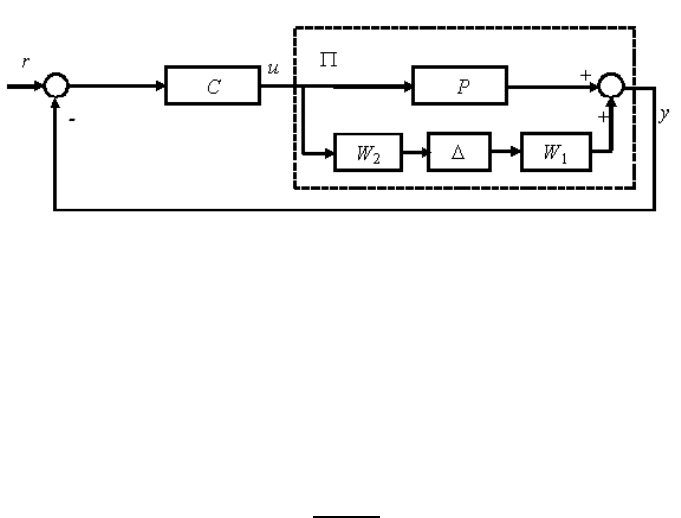
Introduction to Optimal an d Robust Control 103
which is shown in Figure 5.3.
FIGURE 5.3
A closed-loop system wit h additive uncertainty for robust stability analysis.
THEOREM 5.6
[70] Let Π = P + W
1
∆W
2
, and C be a stabilizing controller for the nominal
plant P . Then the closed-loop system is well-posed and internally stable for
all k∆k
∞
< 1 i f and only if kW
2
CSW
1
k
∞
≤ 1 , where
S =
1
1 + P C
. (5.10 2)
Similarly, the closed-loop sy stem is stable f or all stable ∆ with k∆k
∞
≤ 1 if and
only if kW
2
CSW
1
k
∞
< 1.
Multiplicative uncertainty
The system model is described by the fo llowing multiplicative pertur bation:
Π = (I + W
1
∆W
2
)P (5 .103)
where W
1
, W
2
and ∆ are stable. Consider the feedback system shown in Figure 5.4.
THEOREM 5.7
[70] Let Π = (I + W
1
∆W
2
)P , C be a stabilizing controller f or the nominal
plant P , and T = 1 − S. Then
(i) the closed-loop system is well-posed and internally stable for all stable
∆ with k∆k
∞
< 1 if and only if kW
2
T W
1
k
∞
≤ 1.
(ii) the closed-loop system is well-posed and internally stable for all stable
∆ with k∆k
∞
≤ 1 if kW
2
T W
1
k
∞
< 1.
(iii) the robust stability of the closed-loop system for all stable ∆ with
k∆k
∞
≤ 1 does not necessarily imply kW
2
T W
1
k
∞
< 1 .
