Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

124 Modeling and Control of Vibratio n in Mechanical Systems

Through experiments, th e frequency responses of the actual VCM is obtained and

is shown in Fig ure 6.2. A 5th order model is used t o approximate the actual frequency

responses of the VCM actuator and is given by

P (s) =

5.172 × 10

+ 1.82 ×10

s + 3.267 ×10

+ 2.117 × 10

+ 1.032 × 10

+ 1.906 × 10

+8.587 × 10

s + 7.345 ×10

. (6.42)

Figur e 6.2 shows the comparison between the frequency responses of the actual data

and those of P (s). It is clear that their difference is more signiﬁcant for the frequency

range of over 4 kHz. To capture the unmodeled dynamics in high frequencies, dozens

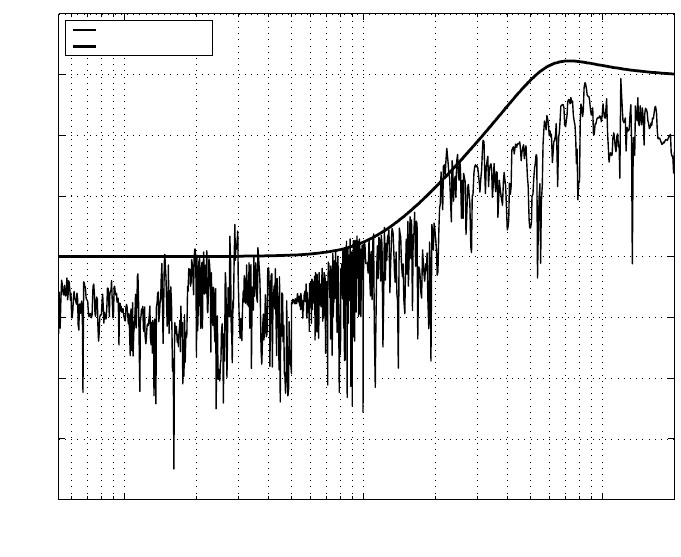
of frequency response measurements are carried o ut and Figure 6.3 shows the multi-

plicative uncertainty of the VCM actuator deﬁned by

∆(ω) =

mea

max

i=1



(jω) − P (jω)

P (jω)



, (6 .43)

where N

mea

is the number of measurements and P

(jω) is the actual frequency

response of the plant in the i-th measurement, and P (jω) is the frequency response

of the model in (6.42). An approximate bounding function W

(s), i.e., the smooth

line in Figure 6.3, is obtained as

(s) =

+ 2.903 × 10

s + 1.433 ×10

+ 3.016 × 10

s + 1.421 ×10

. (6.44 )

From Figure 6.3, it is clear that the uncertainty at frequency over 5 kHz is the major

concern. We observe that the actual uncertainties at some frequencies below 5 kHz

exceed the bounding function, which, however, wil l not cause any major problem.

In fact, we verify that the robust stability of our designed system is guaranteed even

with the worst case of uncertain ty.

By di scretization using the zero-order hold, the corresponding z-domain models

of the VCM and the bounding function, i.e., P (z) and W

(z) can be ob tained.

The dist urbance and noise models D

(s), D

(s) and N(s) are given by (2.42)−(2.44),

and D

(z), D

(z) and N(z) are their di screte-time forms.

As mentioned, one of the most important performance measures for HDDs is the

track misregist ration or TMR, the total amount of random ﬂuctuati on about the de-

sired track location. TMR is used to judge the required accuracy of positioning and

thus to scale the di sk capacity. To achieve a high capacity disk drive, one way in

servo control is to minimize TMR, which is given in terms of the standard devi at ion

of the true PES, i.e.,

3σ

= 3

q − 1

i=1

(i)

, (6.45)

where q is the number of true PES samples.

Mixed H

∞

Control Design for Vibration Rejection 125

−40

−20

Magnitude(dB)

measured

modeled

−1200

−1000

−800

−600

−400

−200

Phase(deg)

Frequency(Hz)

FIGURE 6.2

Frequency responses of the VCM actuator.

126 Modeling and Control of Vibratio n in Mechanical Systems

−60

−50

−40

−30

−20

−10

Frequency(Hz)

Magnitude(dB)

VCM uncertainty

bounding curve

FIGURE 6.3

Multiplicative uncertainty of the VCM actuator.

Mixed H

∞

Control Design for Vibration Rejection 127

Let ˜w = [w

]

and T

denote the transfer function matrix from ˜w to z

When q is large enough, the H

norm of T

is given b y [88]

≈

q − 1

i=1

(i)

. (6.46)

Thus, the control design problem to mini mize TMR can b e treated as an H

optimal

control problem.

On the ot her hand, we need to ensure the system stability against the unmodeled

high frequency dynamics of the VCM actuator, i.e., the constraint kT W

∞

< 1

is to be met, where T is the closed-loop t ransfer funct ion and W

is the bounding

function of the unmodeled dynamics whi ch was derived earlier. Therefore, we have

the mixed H

∞

control scheme as shown in Figure 6.1, where w

∈ ℓ

[0, ∞), a

disturbance input or a reference. Clearly, the transfer function from w

to z

is T W

We now derive the state-space representation (6.1)−(6.4) for the system in Figure

6.1 with

x =





, (6.47)

w =





, (6.48)

A =







0 0 0

0 A

0 0 0

0 0 A

0 0

0 0 0 A

0 B

0 A







, (6.49)







0 0 0

0 B

0 0

0 0 B

0 B

0 0







, B













, (6.50)



−C

0 −C



, (6.51 )



0 −D



, C



−C

0 −C

0 0



z11



0 −D

0 0



, D

z12

= 0, (6.52)



0 D

0 C



, (6.53)

z21



0 D

0 0



, D

z22

= 0, (6.54)

and x

, x

, and x

are respectively the state variables of the VCM actua-

tor P (z), the input disturbance model D

(z), t he ou tput disturbance model D

(z),

the measurement noise model N(z), and the uncertainty W

(z). (A

, B

, C

, D

, B

, C

, D

), (A

, B

, C

, D

), (A

, B

, C

, D

) and (A

, B

, C

, D

)

are respectively the state-space models of P (z), D

(z), D

(z), N(z), and W

(z).

Note that for the servo control shown in Figure 6.1, n

= n

= 1.

128 Modeling and Control of Vibratio n in Mechanical Systems

6.5.2 Design results

In this section, we wi ll apply the mixed H

∞

control to hard disk drive servo

formulated previously. The sampling frequency being used is 20 kHz. By applying

Theorem 6.2 and searching for the optimal scaling parameters, we obtain λ

= 0.3,

= 0.31, λ

= 0.9, ε

= 0.3, ε

= 0.28, ε

= 1.1 and the minimum H

norm,

i.e., the σ value of the tr ue PES z

, of 0.00748 µm.

For the purpose of comparison, we also design a mixed H

∞

controller for the

disk drive using the approach in Theorem 6.1. The minimum H

norm of 0.01013

µm is obtained. Starting from this controller, we carried o ut a further iterative pro-

cedure between controller variables and Lyapunov parameters:

Step 1: obtain th e clo sed-loop system (

D) with the controller parameters

, B

, C

, D

), and let A =

A, B =

B, C =

C, and D =

Step 2: solve LMIs (5.14)−(5.15) , (5 .20) for P and X, and minimize T race(Π).

If T race(Π) does not di ffer from the previo us value, stop. Otherwise, go to step 3.

Step 3: With the obtained P and X, solve LMIs (5.14)−(5.15), and (5.20) for

, B

, C

, D

Step 4: g o to Step 1.

The iterative p rocedure gives a controller that produces a slight impr ovement of

the H

norm, i.e., 0.0100 2 µm. Hence, the improved approach represents about

25.3% more improvement on TMR than the design method in Theorem 6.1 together

with an it erative reﬁnement.

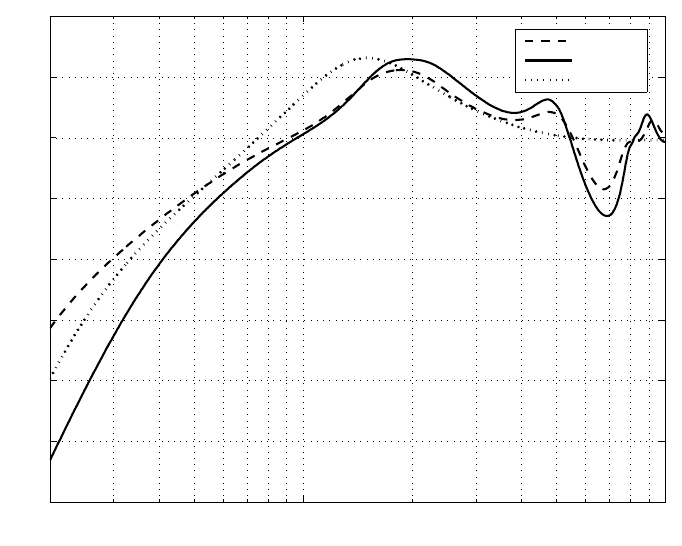
Figur e 6.4 shows the compariso n of sensitivity fu nctions, where we can see that

the sensitivity function designed based on the improved design method is b et ter than

that from Theorem 6.1, except that its hump is slightly higher. The comparison of

control performances obtai ned by the improved metho d and that of Theorem 6.1

is given as in Table 6.1, where the bandwidth from the improved method is much

higher. Although the H

∞

norm of T W

of the improved design is slightly higher

than that of the design using Method 1, it is below one as required, implying the

designed controller makes the closed-loop system robustly stabl e i n the presence of

uncertainty bounded by W

. Further, from Figure 2.23, the disturbance mainly con-

centrates on frequencies below 1 k H z, hence, the slight higher peak does not degrade

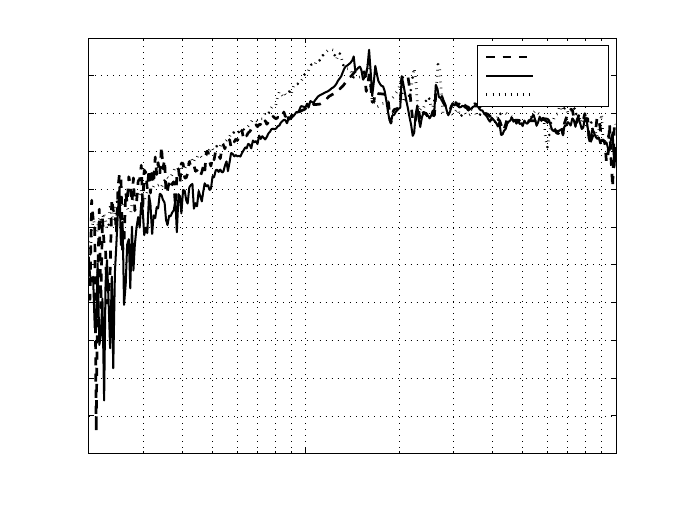
the disturbance rejection performance much. Figure 6.5 shows the testing result of

sensitivit y functions, which is consistent with the simulation results in Figure 6.4.

REMARK 6.6 From Table 6.1, one may argue that a reduced H

norm

for the method of Theorem 6.1 may be obtained by a γ value of greater

than one as the actual H

∞

norm is 0.78, lower than that of the improved

method. However, based on our simulations, no obvious improvement on the

performance has b een observed. For example, wi th γ = 1.5, a slightly

reduced H

norm of 10.11 nm is obtained whereas the actual H

∞

norm is

0.79. With γ = 5, the H

norm is reduced to 10.08nm with an unchanged

∞

norm of 0.78. This means that with a larger γ, the improvement on the

norm for the method of Theorem 6.1 is negligible.

Mixed H

∞

Control Design for Vibration Rejection 129

The improved method is also compared with conventional PID d esign. As shown

in Figure 6.4 and Figure 6 .5, the sensitivity function by PID control has a lower

bandwidth and almost the same peak value, which gives a higher TMR as listed in

Table 6.1.

The previous simulation is carried out with

and

as solutions to the LMI

(6.32). When (3,1) and (3,2) blocks in (6.32) are set to zeros, it is found that the

designed cont roller gives a 9% lower bandwidth for the closed-loop system, leading

to a worse TMR. Thi s demonstrates that the parameter Σ in Lemma 6.1 is useful in

achieving a bet ter performance.

−30

−25

−20

−15

−10

−5

Frequency(Hz)

Magnitude(dB)

Method 1

Method 2

PID

FIGURE 6.4

Frequency response of sensitivity functions.

Next, we shall calculate the H

norm using the measured plant frequency response

as in Figure 6.3 and sensitivity function as in Fig ure 6.5. The sp ectrum of z

is given

= |P (f

)S(f

+ |S(f

+|1 − S(f

|N(f

(6.55 )

130 Modeling and Control of Vibratio n in Mechanical Systems

−45

−40

−35

−30

−25

−20

−15

−10

−5

Magnitude(dB)

Frequency(Hz)

Method 1

Method 2

PID

FIGURE 6.5

Frequency response of sensitivity functions.

Mixed H

∞

Control Design for Vibration Rejection 131

TABLE 6.1

Control performance comparison

Method Method 2 Method 1 PID

Open-loop crossover frequency (Hz) 1.4k 969 976

norm (σ (nm)) 7.48 10.13 12.11

kT W

∞

0.89 0.78 0.27

where f

(k = 1, 2, 3..., K) are frequency points, P (f

) represent s the measured

frequency response of the p lant, and S(f

) is the frequency response of the sensi-

tivit y fun ct ion. The resultant σ value of z

is 0.0 1155, better than 0.02714 with the

controller designed by the method in Theorem 6.1.

6.6 Conclusion

This chapter has presented two design methods for the mixed H

and H

∞

control.

One is a slack variable approach, and another one is a less or equally conservative

design in terms of LMIs that contain more free variables than the conventional ap-

proaches. Those variables offer additional freedoms in op timizatio n, resulting in a

less or equally conservative cont rol design . The improved H

∞

control design

has been applied to hard disk drives to mi nimize the track misregist ration while guar-

anteeing th e system robustness in the presence of actuator uncertainties. Compared

with the slack variable method, the improved desig n result for hard disk drives has

indicated a marked improvement of 25.3% in t he H

norm or the TMR performance

while guaranteeing the system robustness b y satisfying the required H

∞

constraint.

The experimental result validates the advantage of the improved design.

Low-Hump Sensitivity Control Design for

Hard Disk Dri ve Systems

7.1 Introduction

In feedback control systems, sensitivity functions are critical to the determin at ion of

their ability in disturbance and noise rejections. However, Bode has shown the limi-

tation of u sing a feedback structure in terms of an integral constraint on the sensitivity

function, as discussed i n Chapter 5. Brieﬂy speaking, the Bo de integral theorem im-

plies that we canno t have a sensitivity function less than unity at all frequencies using

output feedback w ith a ﬁnite-bandwidth controller. Such a sensitivity function must

amplify the disturbances exist ing in frequencies higher than the system bandwidth.

In view of this, we shall employ the special structure of a secondary actuator system

and design appropriate controllers for primary and secondary actuators such that the

hump of the sensitivity function comes as low as possibl e without the cost of low-

frequency performance. This optimized sensitivity function is expected to minimize

the ampliﬁcation of high- frequency disturbances while attenuating low-frequency

and mid-frequency disturbances. With t his low-hump sensitivity, the dual-stage con-

trol system is able to reduce th e contribution from all existin g disturbances to the

error. Two types of microactuator models are con sidered in this chapter: a MEMS

actuator [102] and a PZT actuator [103]. The purpose is to design controls for the

primary and the secondary actuators such that a low hump of the sensitivity func-

tion can be achieved with the help of secondary actuators. A comparison will be

made to evaluate th e effectiveness of the proposed method for the two microactua-

tors. Besides simulations, an implementation with a PZT microactuator veriﬁes th at

the HDD servo loop design method leads to a low-hump sensitivity f unction.

7.2 Problem statement

Figur e 7.1 shows a dual-stage actuation system w ith one primary actuator P

(s) and

one secondary actuator P

(s), and two parallel controllers C

(s) and C

(s). With

disturbances and noise injected, the error is contributed by the disturbances and noise

133