Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

154 Modeling and Control of Vibratio n in Mechanical Systems

Section 7.4.1, a “ﬂat” sensitivity f unction is impossible. The used sampling rate for

the controller design is 40 kHz. The discrete-time actuator models are obtained using

“zero-o rder-hold” method to ensure that the designed controllers are implementable.

With ω = 2π350, ε = 10

−3.2

, ζ = 0.4 in (7.6), a V CM controller C

(z) is de-

signed as in Figure 7.22 using the H

∞

loop shaping method in the previous section.

Also applying the LMI approach, the controller C

(z) for th e microactuator is de-

signed as in Figure 7.23 with ω = 2π3700, ε = 10

−1.38

, ζ = 1, and M = 0.07

1/2

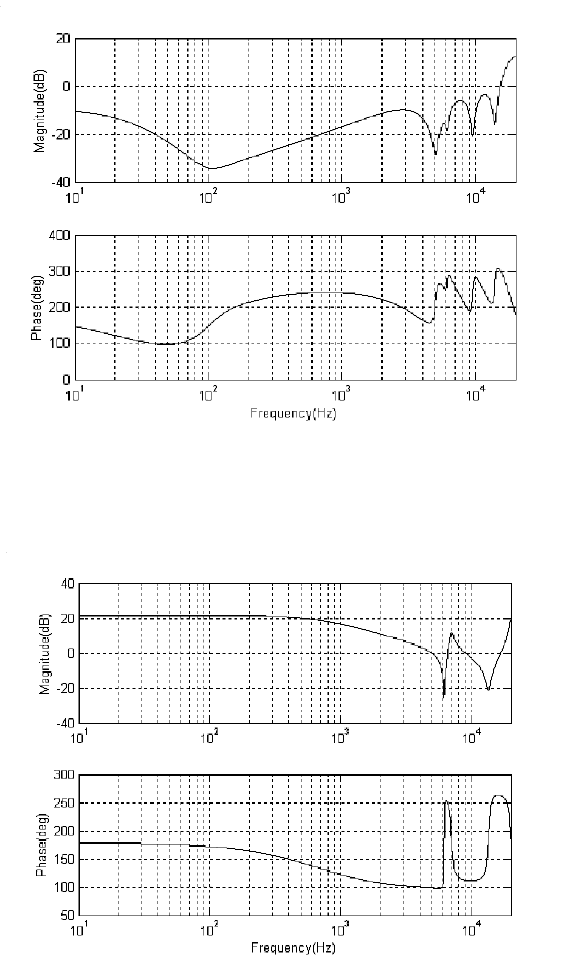
in (7.6). The sensitivity function of the dual-stage system is shown in Figu re 7.24,

where we can observe that the hump is below 3 dB. The open-loop system has the

gain margin of 8.4 dB, t he p hase margin of 64

◦

and the bandwidth of 2.49 k H z.

REMARK 7.2 If manufacturing processes could produce an ideal actu-

ator that can be modeled by a Pade-delay only, which is non-strictly proper,

it is possible to have a “ﬂat” sensitivity like that i n Figure 7. 25 with k

> 0.

An actual microactuator, which resembles the ideal case, is the PZT microactuator

in [107]. It can be described by a 1-pole rol l-off model

(s) =

1257

s + 1.257 × 10

, (7.24)

which is strictly proper and does not satisfy the necessary conditions in Section 7.3.1.

The sensitivity function with the hump lower than 2 dB, as shown as in Figure 7.26,

can be obtained with the same weighting function as that for (7 .14).

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 155

FIGURE 7.22

VCM cont roller C

(z).

FIGURE 7.23

Microactuator controller C

(z).

156 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 7.24

Sensitivity function of the dual-stage system.

FIGURE 7.25

Sensitivity function.

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 157

FIGURE 7.26

Sensitivity function of the dual-stage system.

FIGURE 7.27

Frequency responses of P

(z)C

(z) (solid curve) and P

(z)C

(z) (dashed curve).

158 Modeling and Control of Vibratio n in Mechanical Systems

7.4.3 Implementation on a hard disk drive

The experi metal setup is the same as in Figure 7.17. An LDV wi th a range of 2

µm/V is used to measure the positio n of the dual- stage actuator. Controllers are

implemented with dSpace 1103 on a TMS320C2 40 DSP board. When the dual-

stage loop is cl osed and stabilized with t he desig ned controllers, a swept sine signal

is injected at point A . A DSA is then used to measure the frequency response of

points B over A and o btain the sensitivity function.

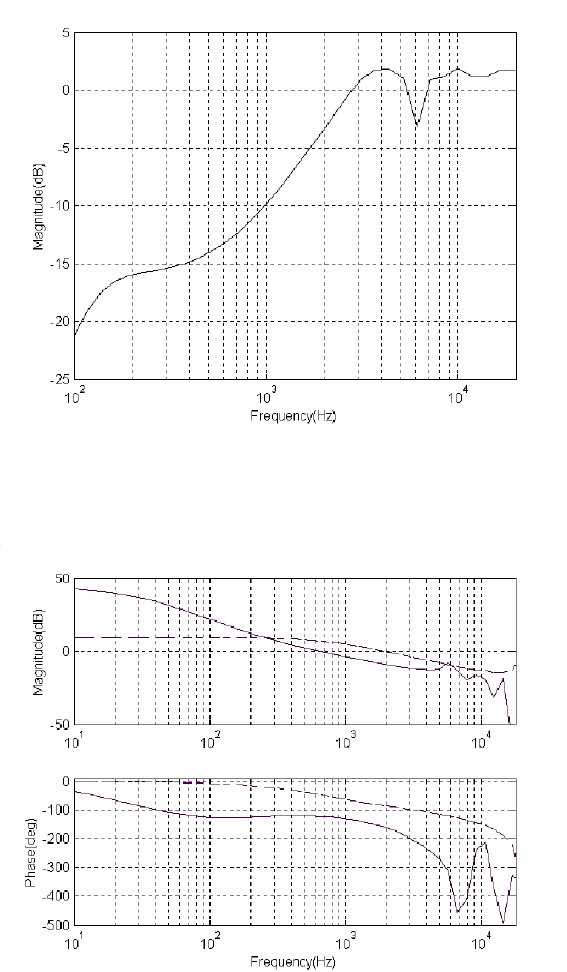
The resultant sensitivi ty functio n is shown in Figure 7.28 , where the rough line is

the testing result and th e smooth line is the simulati on result. We can observe that the

hump of the sensitivity function is lower than 3 dB, which i s better than that by a PID

design as shown by the dott ed line in Figure 7.28. The testing and simulation results

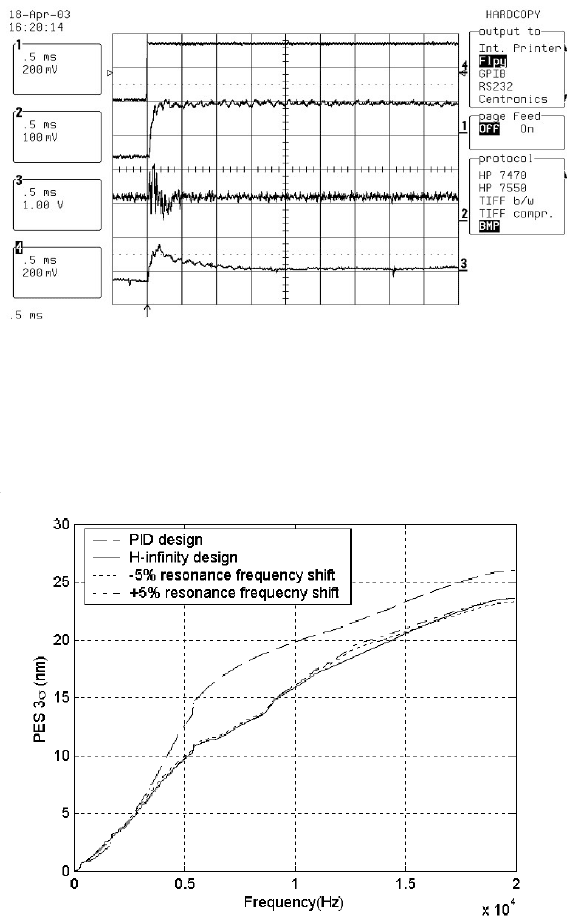
of the dual-stage open loop system are shown in Figure 7.29. The step response in

Figur e 7.30 shows that the system is stabilized and working in real time. Channel 2

in Figure 7.30 is the control signal of the VCM actuator and Channel 3 is the control

signal of the PZT mi croactuator.

The sensitivity function as in Figure 7.28 will amplify the correspon ding high-

frequency disturbances shown in Figure 7.2 du e to the h ump above 0 dB. The po-

sition error i s evaluated from ( 7.1) with the designed sensitivity functions. The 3σ

value of the position error versus frequencies is shown in Figure 7.31, wh ere we can

see that the low-hump design outperforms the PID design for disturbance rejecti on

after 2.4 kHz, which is consistent with Figure 7.28.

The proposed control design is based on the sensitivity w eighting function only

and does not consider robustn ess to plant parameter variations. This, however, will

not hamper the practical application of the resulting controllers due to the large gain

and phase margin s. The system is veriﬁed to maintain stability in spite of the vari-

ation of resonance frequency, e.g., ±5% shift of PZT resonance frequency around

13.5 kHz. The performance change with the presence of the system parameter un-

certainty is ill ustrated in Figure 7.31, where we can see that the perfor mance varies

slightly.

7.5 Conclusion

An H

∞

method has been proposed in both continuous and discrete time domains

to achieve a low-hump sensitivity function for dual-stage HDD systems using an

LMI approach. Two different microactuator models have been studied, w hich are

represented by a MEMS actuator and a PZT actuated suspension. With the proposed

selection of sensitivity weighting functions, the sensitivity function with a hump

below 3 dB has been achieved i n both simulations and experiments. Such a design

process can generate a robust servo controller with high disturbance rej ecti on in a

low frequency range, and less vibration ampliﬁcation in a high frequency range, and

thus is effective in achieving hi gher positioning accuracy.

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 159

FIGURE 7.28

Sensitivity function of the dual-stage system.

FIGURE 7.29

Open loop frequency responses of the dual-stage system.

160 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 7.30

Step response of t he dual-stage system.

FIGURE 7.31

3σ value of PES NRRO versus frequency.

Generalized K YP Lemma-Based Loop

Shaping Control Design

8.1 Introduction

To shape frequency responses of closed-loop transfer functions such as sensitiv-

ity/complementary sensitivity functions, H

∞

optimization together with frequency

weighting is a commonly used method. The additional weight functions, however,

increase the system and controller complexity since the weighting functions usually

have to be of high orders in order to capture the desired speciﬁcations accurately.

This is especially so when a controller is to be designed, aiming at achieving a wider

bandwidth while simultaneously suppressing disturbances of particular f requencies

within or beyon d the servo bandwidth . Further, the process of choosing appropr iate

weights is tedious and time-consuming.

The KYP Lemma [61], being one of the most fundamental results in systems t he-

ory and control, establishes t he equivalence between a frequency domain inequality

(FDI) for a transfer fun ction and a linear matrix inequality associated with its stat e

space realization. I t allows us to characterize various properties of dynamic systems

in the frequency domain in terms of linear matrix inequaliti es. The standard KYP

Lemma is only applicable for the inﬁnite frequency range, while the generalized

KYP Lemma [ 62] establishes the equivalence between a frequency domain p rop-

erty and a linear matrix inequality over a ﬁnite frequency range, allowing designers

to impose performance requirements over chosen ﬁnite or i nﬁnite frequency ranges.

Hence, it is very suitable f or analysis and synthesis problems in practical applications

where different speciﬁcations over different frequency ranges are usually required.

In this chapter, th e generalized KYP Lemma is applied to design a feedback con-

trol such that the speciﬁcations of the sensitivity function, required to suppress some

speciﬁc frequency disturbances, are satisﬁed. Unlike the standard KYP Lemma, the

matrix inequality in the generalized K Y P Lemma involves a matrix variable which is

not necessarily positive deﬁnite and thus the Schur complement cannot be appl ied to

convexi fy the controller design. To overcome this difﬁculty, the Youla parametriza-

tion approach is used to parameterize the closed-loop transfer functi on. The search

for the coefﬁcients of the parameter Q(z) i s then converted t o a linear matri x in-

equality problem within the generalized KYP Lemma framework. An application of

the method in the rejection of narrowband high-frequency and mid -frequency distur-

161

162 Modeling and Control of Vibratio n in Mechanical Systems

bances is presented to demonstrate t he si mplicity of the design and th e improvement

of the positioning accuracy by the resultant controller.

8.2 Problem description

It is known that the power spectrum of the error e in Figure 2.20 is given by

= |P (z)S(z)|

+ |S(z)|

|n|

(8.1)

which implies that the sensitivity function S(z) is important in determini ng the dis-

turbance rejection of a control loop. Thus, the desig n of a controller that g ives

rise to a sensitivity function which can reject speciﬁc disturbances with known fre-

quencies becomes rather signiﬁcant. The purpose here is then stated as: to de-

sign a dyna mic feedback controller C(z) for plant P (z) such that the closed-loop

system is stable and for some prescribed po sitive scalars r

and frequency ranges

, f

), i = 1, ..., N ,

|S(f)| < r

, f

≤ f ≤ f

(8.2)

where S(f) = 1/(1 + C(f)P (f)). Smaller r

means the less contribution of the

disturbance i n frequency range (f

, f

) to the error.

In view of the con straint stated in the Bode integral theorem, it is impossible to

achieve disturbance rejection at all frequencies higher than the bandwid th of the con-

trol loop for actuators or mi croactuators used in mechanical motion systems such as

hard di sk drives. The speciﬁcation (8 .2) is consi dered for a speciﬁc frequency range,

which is however possible to be achieved through shaping the sensitivity functio n.

The above design problem may be approached by selecting a proper frequency

weighting function and carrying out an H

∞

optimization. However, the problem

of how to select a proper frequency weighting function that can give an accurate

shaping of the sensitivity funct ion is generally difﬁcult and time-consuming. Further,

the resultant controller order wil l depend on the order of the weighting function and

the plant. Note t hat a more accurate frequency shaping usually requires a higher

order weigh ting function.

The generalized KYP Lemma [62] gives a necessary and sufﬁcient condition for a

given transfer function to satisfy a required frequency domain property over a ﬁnite

frequency range in terms of a matrix inequality condi tion. Thus, it may be applied to

address the above design prob lem. In what follows, we employ the generalized KYP

Lemma to design a feedback control such that the sensitivity function satisﬁes the

required speciﬁcations so as to reject disturbances at speciﬁc frequencies. In order

to convexify the matrix inequality, the Youla parametrization approach as shown in

Figur e 8.1 is used to design a controller with the generalized KYP Lemma.

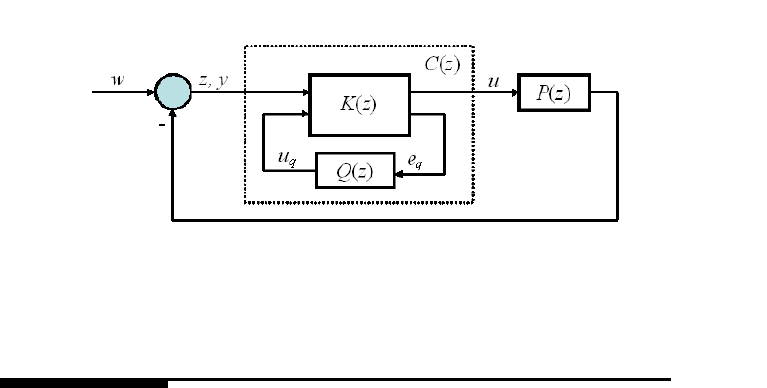
Generalized KYP Lemma-Based Loop Shaping Control Design 163

FIGURE 8.1

Q parameterization for control design.

8.3 Generalized KYP lemma-based control design method

The pr evious analysis indicates that the sensitivity function plays a key role in distur-

bance rejection . To reject disturbance of frequency withi n a certain frequency range,

a proper shaping of the sensitivity function can be carried out. In this section, we

shall present a frequency shaping method based on the generalized KYP Lemma.

First, it is easy to see that the sensitivity function S(z) i s equal to the transfer

function from w to z in Figure 8 .1. The state-space mod el of t he plant under consid-

eration is denoted as (A

, B

, C

, D

). Then, a state-space representation of the

system in Fig ure 8.1 is given by

x(k + 1) = A

x(k) + B

u(k), (8.3)

z(k) = −C

x(k) + w(k) − D

u(k), (8.4)

where x ∈ R

is the state.

Let a state-space representation of th e controller C(z) be given by (A

, B

, C

). Assuming that D = 1 + D

is invertible, then a state-space representat ion

of the sensitivity function can be given by (

D), where

A =



−B

−1

−B

+ B

−1

− B

−1



, (8.5)

B =



−1

−B

−1



C =



−C

+ D

−1

−D

−1



D = 1 − D

−1

. (8.6)

A special case of the generalized KYP Lemma that r elat es the bounded realness of

the sensitivity function over ﬁnite frequency ranges to its st ate space representation

is given b elow.