Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

134 Modeling and Control of Vibratio n in Mechanical Systems

in terms of

= |P

)S(f

+ |S(f

|n(f

, (7.1)

where S

is the power spectrum of the error e, S is the sensitivity function, and

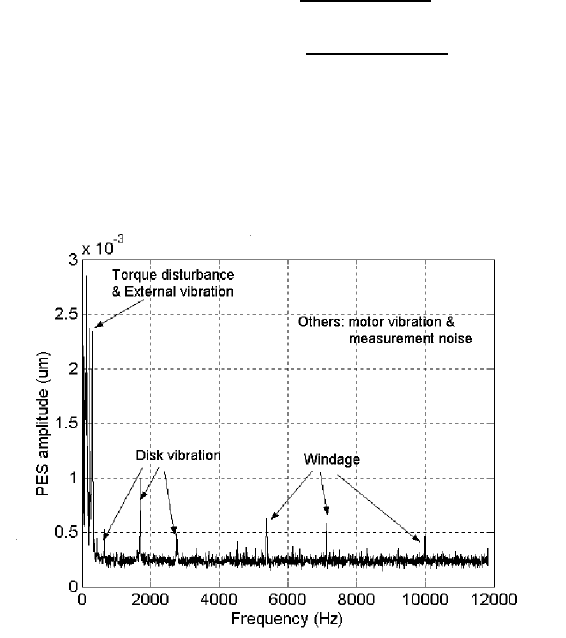
(k = 1, 2, ···, N) are frequency points. Figure 7.2 shows an example of main

disturbances existing in disk drive systems, where the low frequency components are

represented by d

, the higher frequency portion s such as disk vibration and wi ndage

are lumped as d

, and the base line of the spectrum stands f or the noise n.

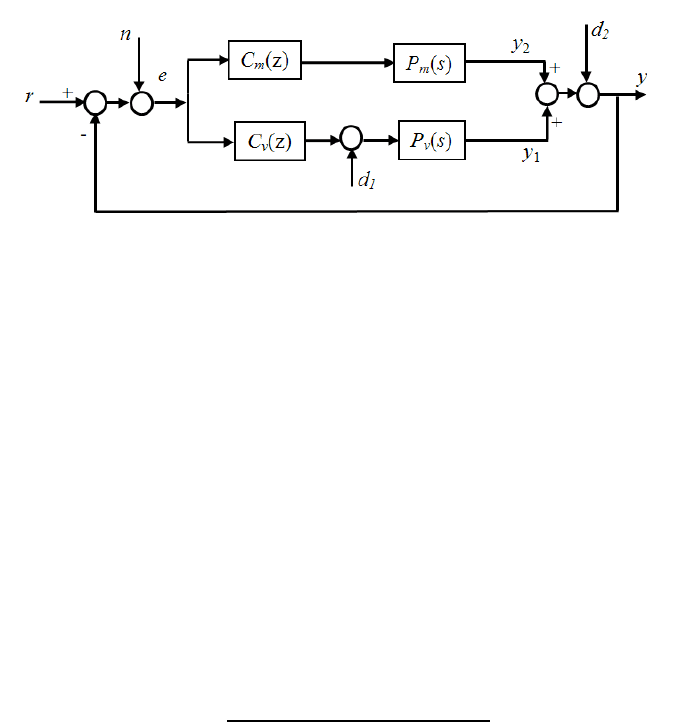
FIGURE 7.1

Parallel structure o f a dual-stage actuation system with disturbances and noise in-

jected.

Equation (7.1) implies that the sensitivity function S is important in determining

the disturbance rejection of the dual-stage closed loop control system. In a conven-

tional single-st age system using one primary actuator it is difﬁcult to have a low-

hump sensitivity fun ction. Thus t he dual- stage structure is applied to increase t he

system b and w idth and lower the sensitivity functio n peak such that

sup |S(jω)| ≤ 1 + τ, ω = 0, ···, ∞ (7.2)

where 0 < τ << 1 is a sufﬁciently small tolerance. The sensitivity function satisfy-

ing (7.2) i s called a nearly “ﬂat” sensitivity function.

A dual-stage actuation system uses a microactuator to increase the system band-

width. Among many contr ol schemes fo r the dual-stage control loop, Figure 7.1 is

one of the most popu lar ones [106]. The overall sensitivity function S(s) is

S(s) =

1 + P

(s)C

(s) + P

(s)C

(s)

. (7.3)

Another popular control scheme is the decoupled structure as shown in Figure 7.3

[101], where the overall sensitivity fun ct ion of the closed-loop system is given by

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 135

cascading each sensitivity function, i.e.,

S(s) = S

(s)S

(s),

(s) =

1 + P

(s)C

(s)

(s) =

1 + P

(s)C

(s)

. (7.4)

In this chapt er we are mainly con cerned with the parallel structure as in Figure 7.1

since it is a basic structure for dual-stage control systems and can be converted to the

decoupled master-slave structure.

FIGURE 7.2

Power spectrum of PES nonrepeatable runout in open loop.

136 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 7.3

Decoupled struct ure of dual-stage actuation systems.

FIGURE 7.4

Structu re of H

∞

loop shaping.

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 137

7.3 Design in continuous-time do main

7.3.1 H

∞

loop shaping for l ow-hump sensitiv ity functions

The H

∞

loop shaping method is u sed to design controllers for the primary actuator

and the microactuator to achieve a low-hump sensitivity fu nction for the du al -stage

actuator system. The structure of the H

∞

loop shaping method is depicted i n Figure

7.4, where W (s) is a weighting function of the desired sensitivity function. For

a plant model P (s), a controller C(s) is to be designed such that the closed-loop

system is stable and

∞

< 1 (7.5)

is satisﬁed, where T

is the transfer function from w to z, i.e., S(s)W (s). Cl early,

(7.5) means that the sensitivity function S(s) can be shaped similarly to the inverse

of the chosen weighing function W (s). A simple form of W (s) is

W (s) =

+ 2ωζ

√

s + ω

+ 2ω

√

εs + ω

, (7.6)

where ω is valued by the desired bandwidth, ε is to determine the low-frequency

level of the desired sensitivity function, and ζ is the damping ratio.

Associated with the weighting function, Fi gure 7.4 can b e fo rmulated as foll ows.

˙x(t) = Ax(t) + B

w(t) + B

u(t), (7. 7)

z(t) = C

x(t) + D

w(t) + D

u(t), (7.8)

y(t) = C

x(t) + D

w(t) + D

u(t), (7.9)

where

A =





, B





, B









, D

= D

, D

= D





, D

= 1, D

= D

, B

, C

, D

) and (A

, B

, C

, D

) are respectively the state-space realiza-

tions of plant P (s) and weighting function W (s). Let (A

, B

, C

, D

) be the state

space description of C(s). Then (A

, B

, C

, D

) is to be designed such that (7.5)

is satisﬁed. An LMI approach stated in Theorem 5.4 is used to design the controller.

It is known that MATLAB functions, say “hinfsyn.m,” are available to design

the controller. However, numerical errors will occur due to the large g ai n of VCM

actuator and will be the hindrance for running the function. Thus, we would rather

use the LMI approach in our application t o the VCM actuator. There always exists

a minimum l evel γ that makes the LMI (5.99) solvable, which gives a sensitivity

138 Modeling and Control of Vibratio n in Mechanical Systems

function closer to the inverse of its weighting function than that given by a larger γ.

Certainly, the solvability is also related to the chosen weightin g W (s), which must

be realistic due to the Bode limitation.

Bode’s integral theorem allows the possibility of a “ﬂat” sensitivity function up to

a frequency of our concern in the continuous time domain, since the integral con-

straint in (5.136) is deﬁned on the frequency range from 0 to inﬁnit y. Equation (7.2)

can be achieved b y choosing appropriate weighting functi ons for S

and S

sep-

arately. One way is to put the peak of S

within the reduction band of S

, as in

Figur e 7.5, and l ower the high-frequency hump of S

. This would need to decrease

the bandwidth of the primary actuator loop and increase the bandwidth of the mi-

croactuator loop, which can be realized by adjusting the weighting functions W

(s)

for the primary actuator and W

(s) for the microactuator. Here, the primary actuator

loop and the microactuator loop are designed separately for the dual-stage parallel

structure. A n additional reason for this is to meet the goals of ensuring t he stability

of the separate primary and microactuator loops and as in Figure 7.6, letting the pri-

mary actuator open loop have a higher gain at low fr equencies and the microactuator

open loop have a higher gain at high frequencies. The dual-stage parallel control

scheme could be formulated as an MIMO problem, however, to satisfy these sp eciﬁc

requirements, the controller design would be more complicated.

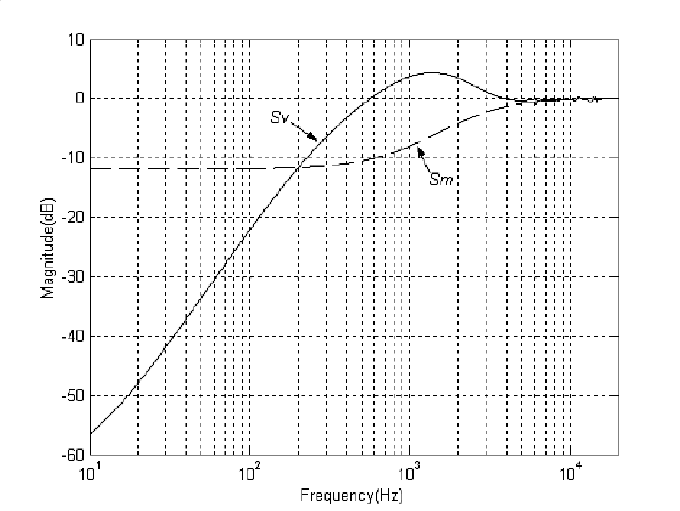
Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 139

FIGURE 7.5

Frequency responses of S

(s) and S

(s).

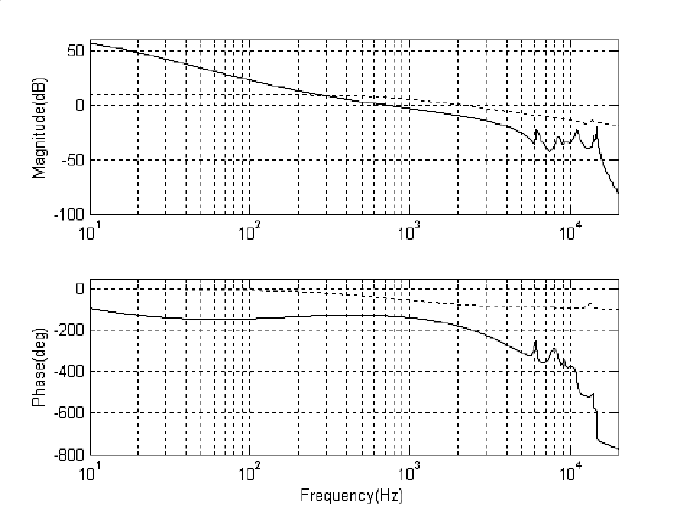
140 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 7.6

Frequency responses of P

(s)C

(s) (sol id line) and P

(s)C

(s)(dotted line).

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 141

7.3.2 Application examples

This section will apply the proposed control design method to a dual-stage actuation

system in hard di sk drives with the structure as in Figure 7.1 such that the designed

controllers can produce a low-hump sensitivity fu nction. The dual-stage HDD uses

a microactuator as a ﬁne positioner t o increase the positioning accuracy. The mi-

croactuator piggyback on a VCM actuator is driven join tly with the VCM actuator

through suspension, slider or head [101]. Due to various microactuator d esigns, two

different microactuator models will be studied and they are coup led separately with

one VCM actuator.

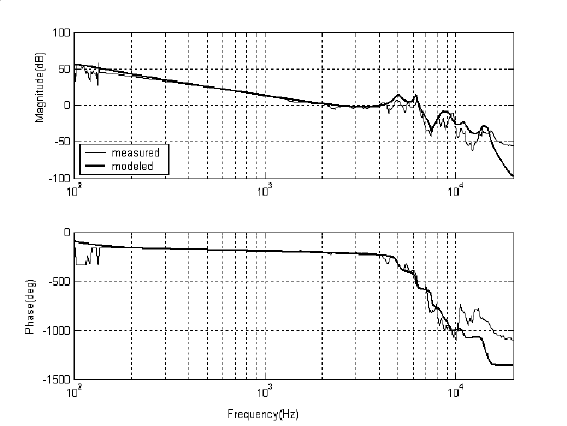
Figur e 7.7 shows the frequency response of the VCM actuator and the po les, zeros

and gain of its model are listed in (7.10)−(7.11). With ω = 2π350, ε = 10

−3.2

ζ = 0.4 in (7.6), VCM controller C

is designed as in Figure 7.8 using the H

∞

loop

shaping method described in th e previous section. The sensitivity functio n |S

(s)| is

shown in Figure 7.5.

FIGURE 7.7

Frequency response of VCM actuator P (s).

poles = [−2312.2122 ± 57759.0421j, −2670.3538 ± 53340.2745j,

−779.1150 ± 38947.95 70j, −942.4778 ± 31401.7862j,

−219.9115 ± 588.5772 j, −18849.5560]; (7.10)

142 Modeling and Control of Vibratio n in Mechanical Systems

zeros = −2356.1945 ± 47064.94 81j,

Gain = 2.127 723028788067 × 10

. (7.11 )

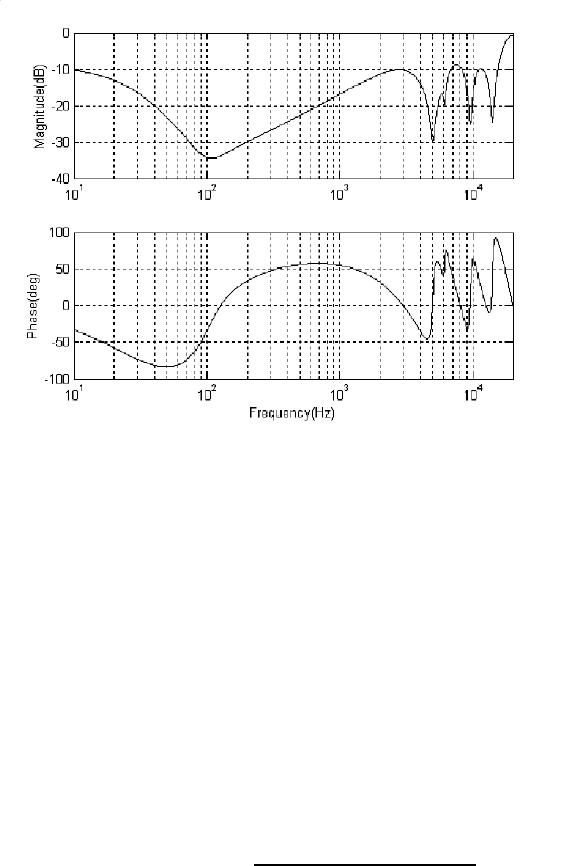
FIGURE 7.8

Frequency response of VCM controller C

(s).

Various microactuators have been proposed for HDD dual-stage servo systems,

including the MEMS actuator and PZT actuator, which are designed by different

mechanism and possess different dynamics. They can generally be characterized by

a pade delay and a 2-pole roll-off model:

P adeDelay × O(s

) (7 .12)

According t o their physical behavior and the locations o f the poles, microactuators

are categorized as two cases. The low-hump design method in Section 7.3.1 will be

applied t o the two cases to investigate t heir effect on the ultimate dual-stage sensi-

tivit y function.

Case 1: Poles are located at low frequency, such as a MEMS actuator [101]

(s) =

2 × 10

+ 282.7s + 8.883 × 10

. (7.13 )

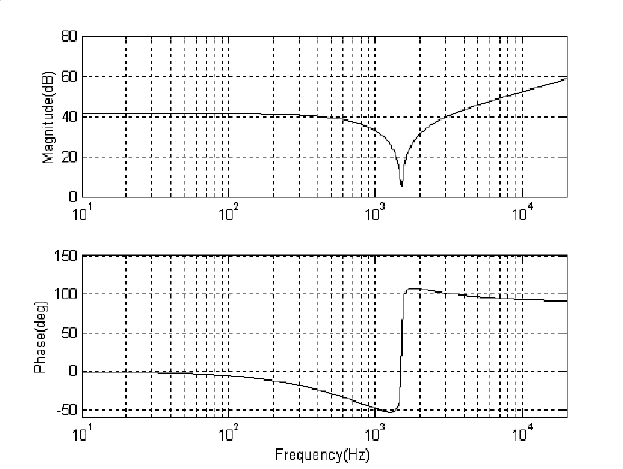
Equation (7.13) is a special case of (7.12) without d el ay. With ε = 1 0

−0.6

, ζ = 1

and ω = 2π2391 in (7.6), the designed controller C

(s) is shown in Figure 7.9.

Low-Hump Sensitivity Control Design for Hard Disk Drive Systems 143

Figur e 7.10 implies that the resultant sensitivity function S

(s) follows its weighting

function closely. The dual-stage servo system has a g ai n margin of 17 d B and a phase

margin of 92

◦

, and its open loop frequency response is shown in Figure 7.11. A

“ﬂat” sensitivity function is achieved as shown in Fig ure 7.12 even though the Bode

integral limitation (5.136) has to be fulﬁlled in this case.

FIGURE 7.9

Frequency response of microactuator controller C

(s).