Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

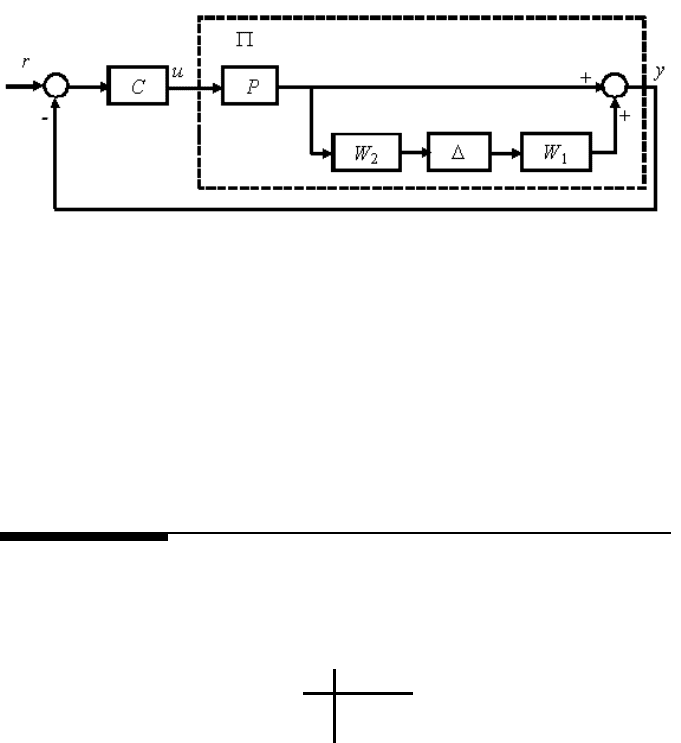
104 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 5.4

A closed-loop system wit h multiplicative uncertainty for robust stability analysis.

(iv) the closed-loop system is well-posed and internally stable for all stable

∆ with k∆k

∞

≤ 1 only if kW

T W

∞

≤ 1.

(v) In addition, assume t hat neither P nor C has poles on the imaginary

axis. Then the closed-loop system is well- posed and internally stable for all

stable ∆ with k∆k

∞

≤ 1 i f and only if kW

T W

∞

< 1.

5.6 Controller parametrization

Consider the standard system block diagram in Figure 5.1 with

P (s) =









. (5.104)

Suppose (A

, B

) is stabi lizable, (C

, A

) is detectable, and D

= 0 . The problem

discussed here is that given a plant P , parameterize all controllers C that internal ly

stabil ize P .

The parametrization for all stabilizing contro llers is k nown as Youla parametriza-

tion [68], as shown in Figure 5.5. The Youla parametrization start s with a nominal

controller that is an estimated-state feedback. The estimated state feedback controller

is given b y

u = −K ˆx, (5.105)

where t he state feedback gain K is some appropriate matrix and ˆx is an estimate of

the component of x, governed by the observer equatio n

ˆx = A

ˆx + B

u + L(y − C

ˆx), (5.106)

Introduction to Optimal an d Robust Control 105

where L is the estimator gain. The transfer function of the estimated-state feedback

controller is thus

(s) = −K(sI −A

+ B

K + LC

)

−1

L. (5.107)

The nominal controller K

(s) will stabilize P provided K and L are chosen such

that A

− B

K and A

− LC

are stable.

To augment t he estimated state f eedback controller, we inject v into u as shown in

Figur e 5.5, meaning that (5.105) is replaced by

u = −K ˆx + v, (5.108)

and therefore the signal v does not induce any ob server error. For the si gnal e we

take the output prediction error :

e = y − C

ˆx. (5.10 9)

In Figure 5.5, the observer b ased contr oller applies output prediction error processed

through a stable transfer f unction Q and added to the output of K

. This augmen-

tation is able to yield every controller th at stabilizes the plant, which means every

stabil izing controller can be realized as an observer based controller with some sta-

ble transfer functio n Q. Thus in the sequel we can form simple state-space equat ions

for t he parametrization of all controllers that stabilize the plant, and all closed-loop

transfer matrices achieved by contr ollers that stabilize the plant.

The state-space equations of the augmented controller are given by

ˆx = (A

−B

K − LC

)ˆx + Ly + B

v, (5. 110)

u = −K ˆx + v, (5.11 1)

e = y − C

ˆx. (5.11 2)

If Q has a state-space realization

˙x

= A

+ B

e, (5.113)

v = C

+ D

e, (5.114)

then a state-space realization of t he observer based cont roller by eliminati ng e and

v from the augmented controller equations (5.110)−(5.112) and t he Q realization

(5.113)−(5 .114) is obtained as:

ˆx = (A

−B

K − LC

− B

)ˆx + B

+ (L + B

)y, (5.115)

˙x

= −B

ˆx + A

+ B

y, (5.11 6)

u = −(K + D

)ˆx + C

+ D

y, (5.11 7)

or equivalently,

C(s) = C

(sI − A

)

−1

+ D

, (5 .118)

106 Modeling and Control of Vibratio n in Mechanical Systems

where



− B

K − LC

−B



, (5.119)



L + B



, (5.12 0)



−K − D



, (5.12 1)

= D

. (5.12 2)

On the other hand, the state-space equations for the closed-loop system with only

the augmented controll er (5.110)−(5.112) are found as follows by eliminating u and

y from (5.110)−(5.112) and the plant equations in (5.104).

˙x = A

x − B

K ˆx + B

w + B

v, (5.12 3)

ˆx = LC

x + (A

− B

K − LC

)ˆx + LD

w + B

v, (5.12 4)

z = C

x − D

K ˆx + D

w + D

v, (5.125)

e = C

x − C

ˆx + D

w, (5.12 6)

which are equivalently written as



(s) T

(s)

(s) 0



= C

(sI − A

)

−1

+ D

, (5.127)

where



−B

K − LC



, (5. 128)





, (5.12 9)



−D

− C



, (5.13 0)





. (5.13 1)

It has been veriﬁed that by augmenting the stable transfer function Q, the closed-

loop transfer function from w to z is simpl y an afﬁne function of Q and equals

+ T

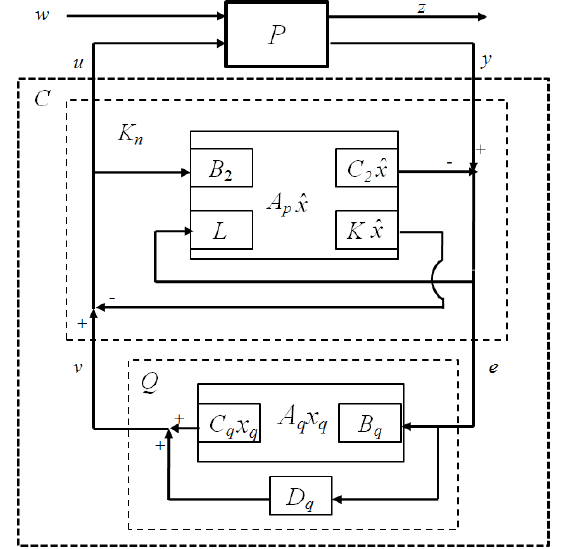
Introduction to Optimal an d Robust Control 107

FIGURE 5.5

Control system structure for Youla parametrization.

108 Modeling and Control of Vibratio n in Mechanical Systems

5.7 Performance limitation

5.7.1 Bode integral constraint

The block diagram in Figure 2.20 shows a typ ical closed-loop control sy stem. The

closed-loo p transfer function from r to y is given by

T =

P C

1 + P C

. (5.132)

The sensitivity function is also known as the disturbance rejection function or error

rejection f unction, and given by

S =

1 + P C

. (5.13 3)

Note that

S + T ≡ 1, (5.13 4)

hence T is also commonly called the complementary sensitivity function.

Denote T

the transfer function from d

to y. In Figure 2.20 , note that

S = T

= −T

= T

. (5.13 5)

The sensitivity function is thus important, because it explains how disturbance d

goes through the closed-loop system and shows up at the outpu t y, or the error signal

e. It is also important to understand how noise n will be ﬁltered throug h the closed-

loop system.

The Bode p lot of sensitivi ty functio n in continuous-time domain i s shown in Fig-

ure 5.6. It can be explained by the following Bode integral theorem.

THEOREM 5.8

[67] Bode’s Integral Theorem for Continuous-time Systems For a stable, ra-

tional P and C with P (s)C(s) having at least 2-pole roll oﬀ,

∞

log|S|dω = 0. (5.136)

An implication of Theorem 5.8 is that if the system is made less sensitive to dis-

turbance at some frequencies, it wi ll be more sensitive at other frequencies. If the

plant P or compensator is not stable, i.e., if P (s) and /or C(s) have a ﬁnite n umber

of unstable poles p

, then (5.136) becomes

∞

log|S|dω = 2π

k=1

Re(p

) > 0, (5.137)

Introduction to Optimal an d Robust Control 109

where K is the number o f unstable poles. Equation (5.137) implies that any unstable

poles in the system only make it worse, in that more of the d isturbance would have

to b e ampliﬁed.

Figur e 5.7 means that for a discrete-time system, the main difference is the N yquist

frequency limits the frequency range we h ave to work with. In both cases, if we

want to attenuate disturbances at one frequency, we must amplify so me disturbance

at another frequency.

THEOREM 5.9

[108] Bode’s Integral Theorem for Discrete-ti me Systems Given a stable closed-

loop di screte-time feedback system, its sensitivity function has to satisfy the

following integral constraint:

log|S(e

jφ

)|dφ =

k=1

ln|β

|, (5.138)

where β

are the open-loop unstable poles of the system, K is the total number

of unstable poles, and φ = T

ω with the sampling time T

and the frequency

ω in radians/sec.

Note that T

is the sampl ing period, and t he upper limit of t he frequency spectrum

is π/T

, the Nyquist frequency. Typical digital cont rol systems assume P C is small

and |S| ≈ 1 at or above the Nyq uist frequency, which is in general not practical for

a ph ysical system. Further research beyond Nyqu ist frequ ency is needed to address

vibrations at frequencies above the Nyquist frequency, which strives to overcome the

limitation due to the i ntegral theorem.

Theorem 5.9 implies that if for some frequency |S| < 1, then at some other fre-

quency | S| > 1. Unlike the continuous ti me result , there is n o inﬁnite bandwidth to

spread this over. Thus all |S| > 1 happen below the Nyquist frequency, and there-

fore in a ﬁnit e frequency range. Since the theorem is limited by frequencies up to the

Nyquist frequency, if the closed-loop bandwidth is p ushed up, better p erformance at

low frequency may result in worse performance at high frequency. In a word, with

the li near feedback control whenever we improve the disturbance rejection at one

frequency we pay for it at another. Nevertheless, if we have sufﬁcient knowledge

of system distur bance and place the disturbance ampliﬁcation at places where the

disturbance is negligible, then we succeed. Otherwise, most of the disturbances may

be ampliﬁed.

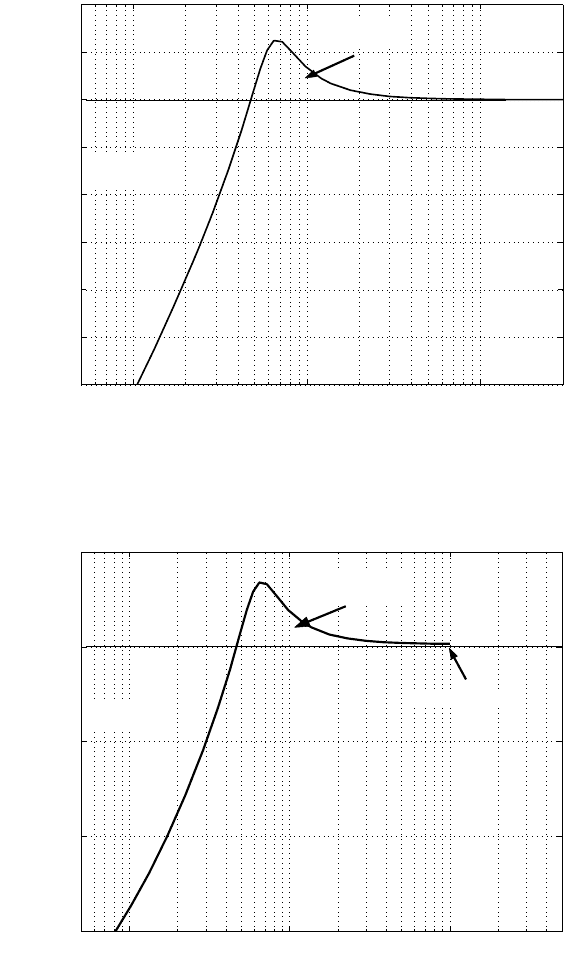
110 Modeling and Control of Vibratio n in Mechanical Systems

Frequency(Hz)

Magnitude in dB (20log

|S|)

Area of vibration

rejection

Area of vibration

amplification

FIGURE 5.6

Sensitivity function for continuous-time system.

Frequency(Hz)

Nyquist frequency

Area of vibration

rejection

Area of vibration

amplification

Magnitude in dB (20log

|S|)

FIGURE 5.7

Sensitivity function for discrete-time system.

Introduction to Optimal an d Robust Control 111

5.7.2 Relationship between system gain a nd phase

In the classical feedback theory, the Bode’s gain- phase integral relation has been

used as an i mportant tool to express design constraints in feedback systems. Let

L = P C denote t he open-loop system. It is noted that ∠L(jω

) will be large if

the gain L attenuates slowly near ω

and small if it attenuates rapidly near ω

. The

behavio r of ∠L(jω) is particularly important near the crossover frequency ω

, where

|L(jω

)| = 1, and π + ∠L(jω

) is the phase margi n of the feedback system. Further

|1 + L(jω

)| = |1 + L

−1

(jω

)| = 2|sin

π + ∠L(jω

)

| (5.139)

must not be too small for good stability robustness. If π + ∠L(jω

) is forced to be

very small by rapid gain attenuation, the feedback system will amplify disturbances

and exhibit little uncertainty tolerance at and near ω

. A non-mi nimum phase zero

contributes an addit ional phase lag and imposes limi tations upon the roll off rate of

the open-loop gain. Thus the conﬂict between attenuation rate and loop quality near

crossover is clearly evident.

In the classical feedback control theory, it has been common to express design

goals in terms of the shape of the op en-loop transfer fu nction . A typical design

requires that the open-loop transfer function h as a h igh gain at low frequ encies and

a low gain at high frequencies while the transition should be well behaved [70].

5.7.3 Sampling

Mathematical relations and operations can be handled by digital microprocessor only

when they are expressed as a ﬁn ite set of numbers rather than as functions having

an inﬁnite number of possible values. Thus any measured continuous signal must

be converted to a set of pulses by sampling, which is the process used to measure a

continuous-time variable at separated instants of time. The inﬁnite set of numbers

represented by the smooth curve is replaced by a ﬁnite set of numbers. Each pulse

amplitude is then rounded off to one of a ﬁnite number of levels depending on the

characteristics of the converter. The process is called quantization. Thus a digital

device is one in which signals are quantized in both time and amplitude. In an analog

device, signals are analog; that is, they are continuous in time and are not qu antized

in amplitude. The device that performs the sampling, quantization, and converting

to b inary form is an analog to digital (A/D) converter.

The number of binary digits or bits generated by the device is its word length,

which is an important characteristic related to t he resolution o f the converter. The

resolution measures the smallest change in the input signal that will produce a change

in the output signal. An example is that if an A /D converter has a word length of 10

bits or more, an input sig nal can be resolved to 1 in 2

or 1024. If the input sig nal

has a range of 10 V, the resolution is 10/10 24, or approximately 0.01 V. Thus i n

order to produce a change i n th e output the input must change by at least 0.01 V.

A discrete-time signal is ext racted by sampling from a continuous-time signal. If

the sampling frequency is not selected properly, the r esulting sampled sequence will

112 Modeling and Control of Vibratio n in Mechanical Systems

not accurately represent the origi nal continuous signal. A proper sampling frequency

is readily determined in many cases by means of the following sampling theorem.

THEOREM 5.10

Sampling Theorem A continuous-time signal y(t) can be reconstructed from

its uniforml y sampled values y(KT

) if the sampling period T

satisﬁes

≤

¯ω

(5.14 0)

where ¯ω is the highest frequency contained in the signal, that is, |Y (ω)| = 0

for ω > ¯ω.

If a system involves a sampling operation of continuous-time signals t o gener-

ate discrete-time signals, a time delay may be induced. Any time delay added in to

a closed-loop control system will decrease the stability of the system and in some

cases may even cause system instability. The Nyquist rate shown in Figure 5.7 signi-

ﬁes that the freedom to spread the ampliﬁcation area around is limited by the Nyquist

frequency, which is half of the sampling rate. Fig ure 5.7 implies that a certain rejec-

tion amount | S| < 1 must be accompanied by a certain area of |S| > 1, which has

to o ccur before th e Nyquist frequency. With a higher sampling rate and closed-loop

system bandwidth being kept constant, the ampliﬁcation |S| > 1 will essent ially

spread over a broader frequency band and the height of ampliﬁcation hump shrinks,

as shown in Figure 5.8. If we push the closed-loop system bandwidth from f

to f

as seen in Figure 5.8, better performance in low frequency range may result in worse

performance in high frequency range.

5.8 Conclusion

Before presentating a series of advanced vibration control methodologies, this chap-

ter has been used to recall some standard advanced control techniques, which hel ps

understand problems to be addressed in the later chapters and possible solutions. It

has reviewed H

and H

∞

performances, H

and H

∞

controls, robust control , con-

troller parametrization, as well as performance limit at ion of linear feedback control

systems.

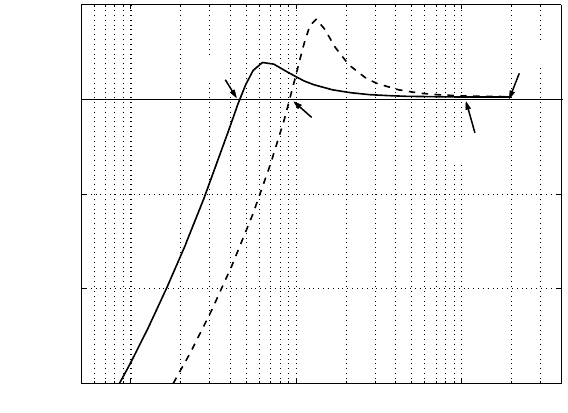
Introduction to Optimal an d Robust Control 113

Frequency(Hz)

Magnitude in dB (20log

|S|)

FIGURE 5.8

Sensitivity function in discrete-ti me domain.