Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

194 Modeling and Control of Vibratio n in Mechanical Systems

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0.5

1.5

2.5

x 10

−3

Frequency (Hz)

NRRO magnitude (µm)

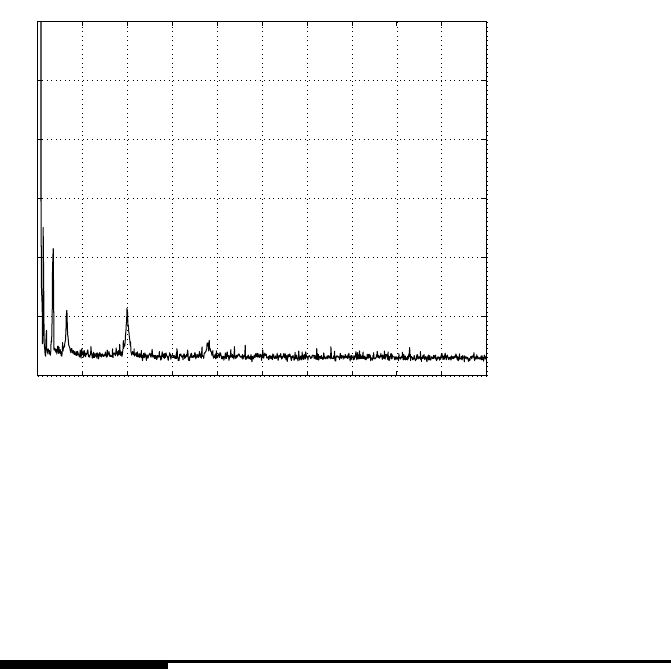
FIGURE 9.7

PES NRRO spectrum without servo control.

plotted in Figure 9.8 and Figure 9.10, respectively. The NRRO spectrum of the sys-

tem with the designed controll er is shown in Fig ure 9.11. Based on Figure 9.11, the

attenuation of disturbance centering at 2 kHz has improved by 35%.

9.5 Conclusion

This chapter h as addressed a combined control design method that incorporates the

generalized KYP Lemma-based design and the H

optimization. With the incorpo-

rated contro l design method, speciﬁc narrowband disturbances have been attenu ated

and simultaneously the positionin g error of the control system has been minimized.

The metho d has been applied to design a controller for a PZT microactuator to at-

tenuate disturbances at 650 Hz and 2 kHz where disk vibrations are dominant and

minimize the 3σ value of the overall PES. Simulation and experimental results have

demonstrated the effectiveness of the proposed method and veriﬁed that the position-

ing accuracy has been improved.

Combined H

and KYP Lemma-Based Control Design 195

−60

−40

−20

Magnitude (dB)

−800

−600

−400

−200

200

Frequency (Hz)

Phase (deg)

Simulation

Experiment

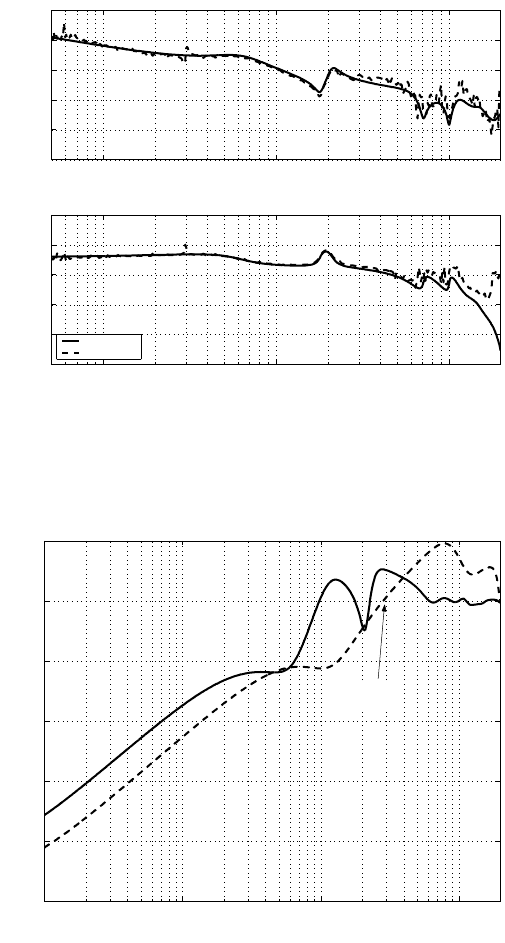
FIGURE 9.8

Open-loop frequency response.

−50

−40

−30

−20

−10

Magnitude (dB)

Frequency (Hz)

Bandwidth is

increased

FIGURE 9.9

Resultant sensitivity function (Solid line: with Spec. (i), (ii) and (iii); Dashed line:

with Spec. (i) and (ii)).

196 Modeling and Control of Vibratio n in Mechanical Systems

−30

−25

−20

−15

−10

−5

Frequency (Hz)

Magnitude (dB)

Simulation

Experiment

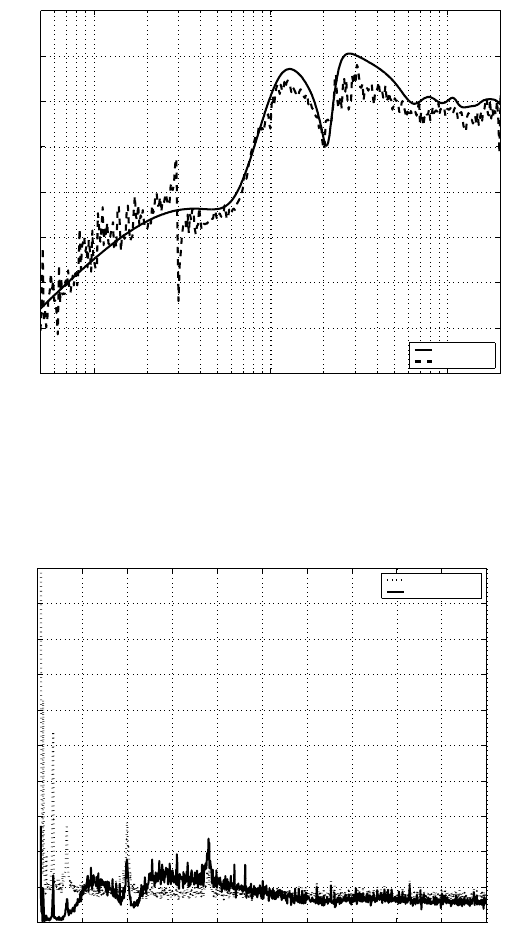
FIGURE 9.10

Resultant sensitivity function with all the thr ee requirements fulﬁll ed.

0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

x 10

−3

Frequency (Hz)

NRRO magnitude (µm)

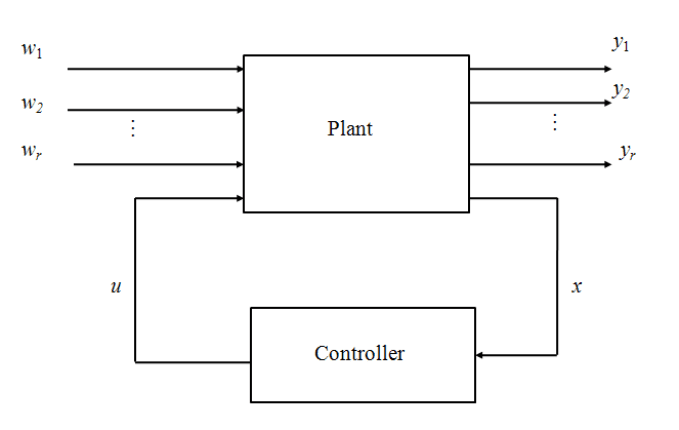
Without control

Closed loop

FIGURE 9.11

NRRO power spectrum with rejection of two speciﬁc disturbances at 0.65 and 2 kHz.

Blending Control for Multi-Frequency

Disturbance Rejecti on

10.1 Introduction

The blending control technique [120] aims to design a controller capable of simul-

taneously coping wi th different optimality criteria deﬁned for variou s input-output

channels. If several targeted transfer functions are achieved respectively by their

designed controllers, it is shown that u nder some mild assumptions there exists a

unique controller capable of replicating these transfer functio ns and thus simultane-

ously achieving the performance attained b y each individual controller. Each indi-

vidual controller can be a static or a dynamic feedback controller derived by means

of standard opt imal and robust control methods such as the LQG/LTR control, H

∞

control. The blended contr oller can be easily computed by a procedure based on

simple linear algebra. In this chapter, we shall apply the blending control idea to deal

with the problem of rejecting several narrowband disturbances. The multi-frequency

disturbance rejection is for mulated as a control blending p roblem. Control design for

each disturbance rejection is carried out by using the H

optimal control method. The

ultimate controller is obtain ed by blending all these H

controllers and is expected

to be abl e to reject all these disturbances simultaneously. In this chapter, the con-

trol bl end ing is respectively app lied in the control design for a 1.8-inch H D D V CM

actuator in three cases, (1) reject two disturbances of frequencies higher th an band-

width, (2) reject three disturb ances w ith frequencies higher than bandwidth, and, (3)

reject one disturbance with frequency lower than bandwidth and another one higher

than bandwidth. Note that this chapter presents a syst ematic approach using dis-

turbance models on ly, which leads to t he achievement of a satisfactory rejection of

multi-frequency narrow band disturbances.

10.2 Co ntrol bl ending

Control blending accoun ts for the problem of simultaneous performance achieve-

ments. It involves designing an individual controller for each perfor mance speciﬁca-

197

198 Modeling and Control of Vibratio n in Mechanical Systems

tion and blending all the controllers to obtain an ultimate cont roller.

Consider the system in state space:

˙x(t) = Ax(t) + Bu(t) +

i=1

(t), (10.1)

(t) = C

x(t) + D

u(t), (10.2)

(t) = C

x(t) + D

u(t), (10.3)

···

(t) = C

x(t) + D

u(t), (10.4)

e(k) = C

x(k) + D

u(k) + v (k), (10.5)

where x(t) ∈ R

, u(t) ∈ R

, y

(t) ∈ R

, w

(t) ∈ R

, e(t) ∈ R, and A, B, C

, E

, C

, and D

are matrices of approp riate dimensions.

The following two assumption s are necessary in the control blending scheme.

Assumption 10.1: (A, B) is stabilizable.

Assumption 10.2: The n

×s matrix,

E =



··· E



, (10.6)

where s =

i=1

, h as full column rank.

FIGURE 10.1

Blending control scheme.

Blending Control for Multi-Frequency Disturba nce Rejection 199

10.2.1 State feedback control blending

The feedback control scheme of the above system is shown in Figure 10.1, where the

controller is expressed as

˙x

(t) = A

(t) + B

x(t) (10.7)

u(t) = C

(t) + D

x(t). (1 0.8)

The closed-loop system fro m w

to y

, i = 1, 2, ···, r is then described by











A + BD

··· E

0 0 ··· 0

+ D

0 0 ··· 0

+ D

0 0 ··· 0

. ···

+ D

0 0 ··· 0







. (10.9)

For the system ( 10.1)−(10.5), we consider the static state feedback control

u(t) = K

x(t), i = 1, 2, ···, r. (10.10)

The individual closed-loop tr ansfer function is given by

(s) =

(sI −

)

−1

, (10.11 )

with

= A + BK

= C

+ D

. (10.12)

The result in [120] reads t hat there exists a single dynamic compensator of the

form (10.7)−(10.8) of o rder µ = n

(r − 1), such th at 1). the closed-lo op system is

stable with spectrum

σ(A

) =

∪

σ(

); (10.13)

and 2). for each i, the transfer function T

(s) from the i

input to the i

output

coincides with the one given by the i

gain K

, i.e.,

(s) =

(s). (10.14)

The signiﬁcance of the result lies in the fact that if K

, i = 1, 2, ···, r, are the

static compensators each of which optimizes some performance criteria, then there

exists a single dynamic compensator which simultaneously achieves the same per-

formances. The single dynamic compensator of the form in (10.7)−(10.8) can be

found following the procedure below.

Procedure 10 .1

200 Modeling and Control of Vibratio n in Mechanical Systems

• Let K

, i = 1, 2, ···, r be th e stat ic state feedback controllers each of which

asymptotically stabilizes the plant, i.e.,

= A + BK

is asymptotically

stable.

• For each i, cho ose a matrix

of dimension n

×(n

−q

) such that [E

]

is square and invertibl e. This is possible under Assumption 10.2.

• Choose matrices

of dimension µ ×(n

−q

) (µ = n

(r −1)) such that the

matrix



··· E

···

0 0 ··· 0

···



(10.1 5)

is invertible.

• Deﬁne

= [0

][E

]

−1

, (10.16)

and

= Z

. (10.17)

• Form the square matrix Ξ as

Ξ =



I I ··· I

··· Z



. (10.18)

• Compute th e controller matrices A

, B

, C

, D







··· K

··· V



−1

. (10.19)

The or der of th e blended controller is n

(r −1) which is very hi gh. Theoretically

to match r different transfer functi ons T

, n

(r − 1) + n

= n

r different poles

have to be allocated and a full order contr oller is required. In practical application,

however, reducing the order is needed as long as it i s possibl e.

10.2.2 Output feedback control blending

When the full state variables of the plant are not available, the feedback control has

to rely on some measurements given by

(t) = C

x(t), (10.20)

where y

∈ R

. The output feedback control ler takes the form

˙x

(t) = A

(t) + B

y(t) (10.21)

u(t) = C

(t) + D

y(t). (10.22)

Blending Control for Multi-Frequency Disturba nce Rejection 201

The closed-loop system fro m w

to y

, i = 1, 2, ···, r is th en descri bed by











A + BD

··· E

0 0 ··· 0

+ D

0 0 ··· 0

+ D

0 0 ··· 0

. ···

+ D

0 0 ··· 0







. (10.23)

Assumption 10.3: The composed p × s matri x,

E =



··· C



, (10.24)

where s =

i=1

, h as full column rank.

Consider the static st at e feedback control as stabilizing compensators

u(t) = K

x(t), i = 1, 2, ···, r. (10.25)

The corresponding cl osed-loop transfer function from w

to y

is given b y

(s) =

(sI −

)

−1

, (10.26 )

with

= A + BK

= C

+ D

. (10.2 7)

The th eorem on output blending control in [120] says that there exists a single

dynamic compensator of the form (10.21)−(10.22) of or der µ = n

r − p, su ch that

1). the spectrum of the closed-loop system satisﬁes

∪

σ(

) ⊆ σ(A

); (10.28)

and 2). for each i, the transfer functio n T

(s) from the i

input w

to the i

output

coincides with the one given by the i

gain K

, i.e.,

(s) =

(s). (10.29)

The single d ynamic output controller of the form in (10.21)−(10.22) can be found

following the procedure below.

Procedure 10 .2

• Let K

, i = 1, 2, ···, r b e the static state feedback controllers each of which

asymptotically stabilizes the plant, i.e., the matrix

= A + BK

is asymp-

totically stable.

• For each i, choose a matrix

of dimension n ×(n −q

) such that [E

] is

square and invertible. This is possi ble under Assumption 10.3.

202 Modeling and Control of Vibratio n in Mechanical Systems

• Choose matrices

of dimension µ × (n

− q

) (µ = n

r − p) such that the

matrix



··· C

0 0 ··· 0

···



(10.3 0)

is invertible.

• Deﬁne

= [0

][E

]

−1

, (10.31)

and

= Z

. (10.32)

• Form the square matrix Ξ as

Ξ =



··· C

··· Z



. (10.33)

• Compute th e controller matrices A

, B

, C

, D







··· K

··· V



−1

. (10.3 4)

The procedure is quite simple to implement, and it is proved in [120] that the

matrix Ξ is indeed an invertible matrix.

Consider the system



N 0









0 ··· 0 E

0 ··· 0

··· 0 0 E

··· 0

. ···

0 0 ···

0 0 ··· E

··· C

0 0 ··· 0







. (10.35)

The following Proposition advises on the stabilit y of the controller matrix A

Propositi on 10.1 [120]

i). The controller matrix A

is not stab le if system (10.35) h as unstable invariant

zeros.

ii). The controller matrix can be generically chosen as a stability matrix if system

(10.35) is of minimum phase.

iii). If E is sq uare then the controller matrix is sta ble if and onl y if system (10.35)

is of minimum ph ase.

Blending Control for Multi-Frequency Disturba nce Rejection 203

10.3 Co ntrol blending ap plication i n multi-frequency disturbance

rejection

In this section, we ﬁrst formulate the problem of multi- frequency disturbance rejec-

tion into the above control blending framework. Then, Procedure 10.1 is used to

design a blended controller associated with the static state feedback contr oller de-

signed via th e H

optimal control method. To facilitate the single dy namic state

feedback controller, a full state observer i s required.

10.3.1 Problem formulation

The closed con trol loop of a mechanical actuation system is shown in Figure 10.2,

where P (s) is the actuator model, C(z) is the feedback controller, e is the measured

error signal. D

(s), i = 1, 2, ···, r are disturbance models and w

are white noises

with unity variances. v is the measurement noise with σ

as its standard deviation.

Here, we focus on the rejection of output disturbance D

(s), considering that an

input disturbance can be converted to an output disturbance.

From Figure 10.2, with Ref = 0 we have

y = S(z)(D

(z)w

+ D

(z)w

+ ···+ D

(z)w

) + (1 − S(z))v. (10.36)

The multi-frequency disturbance rejection problem is stated as fo llows: For nar-

rowband disturbances d

, i = 1, 2, ···, r, desig n a feedback controller C(z) such

that the closed-loop system i s stable, and the disturbances d

in different frequency

ranges [f

, f

] can be suppressed simultaneously.

In Fig ure 10.2, denote (A

, B

, C

, D

) as the state-space realizations of P (z)

with state vector x

∈R

, and (A

, B

, C

, D

) as the state-space realizations

of D

(z) with state vector x

∈R

. D

(s) is proposed to have the form:

(s) =

(s + 2ζ

)

+ 2ξ

s + ω

, i = 1, 2 , ···, r, (10.37)

with frequency ω

, damping ratio ξ

, ζ

used to adjust the damping of D

, and gain

. Clearly, D

= 0.

To ensure necessary rejection of low-frequency disturbances, a pre-compensation

integrator Int(z) is introduced which is shown in Figure 10.3 and given b y

˜u(k + 1) =

ke(k) + ˜u(k). (10.38 )

Denote the output due to d

by y

. Then the combined system is given as fo llows.

x(k + 1) = Ax(k) + Bu(k) +

i=1

(k), (10.39)

(k) = C

x(k) + D

u(k), (10.40)