Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

∞

-Based Design for Disturbance Observer

11.1 Introduction

The idea of observing disturbance to improve the performance of a servomechanism

was ﬁrst intr oduced in [123]. It was suggested t hat if the disturbances were supp os-

edly generated by a linear dynamic system and the model of the syst em was known,

they could be estimated from the system output measurement by an asymptotic esti-

mator (Luenberger observer) and the effect of the dist urbances could be neutralized

by feeding the disturbance estimates back into the system [124]. Over the years, the

method has been modiﬁed and applied. However, it is not always easy to ident ify the

disturbance model. Furt her, it is not always true that the disturbance model is linear

time-invariant. Subsequently, a new type of disturbance observer (DOB) has been

introduced [128]. This new method does not require control designers to have the

full in formation of the distur bance model and does not need the assumption that the

disturbance model is linear time-invariant. However, it requires the model of th e con-

trolled plant to be accurately known and invertible, at least within the bandwidth of

interest [1 29]. Recently, it has been proven that under certain assumptions imposed

on the plant and disturbance models, the two different methods are equivalent in that

the original d isturbance observer introduced in [ 123] is actually a generalizatio n of

the latter metho d [126]. In this chapter, we study the latter method where a g eneral

form of distu rbance observers, which does not need to so lve the plant model inverse,

will be introduced.

If majority of the disturbances are of r el atively lower frequency, when a DOB

is added on to attenuate the effect of disturbances, the standard and conventional

way of designing a Q-ﬁlter is to design it to be a low-pass ﬁlter with unity DC gain

[128]. In this chapter, we introduce the conventional disturbance observer ﬁrst, and

then present a general form of dist urbance observer. An H

∞

control based method is

applied to the design of a Q-ﬁlter. The designed disturbance observer is applied to an

HDD servo system and its effectiveness in distur bance attenuation is demonstrated

by simulation s and experiments.

215

216 Modeling and Control of Vibratio n in Mechanical Systems

11.2 Co nventional disturban ce observer

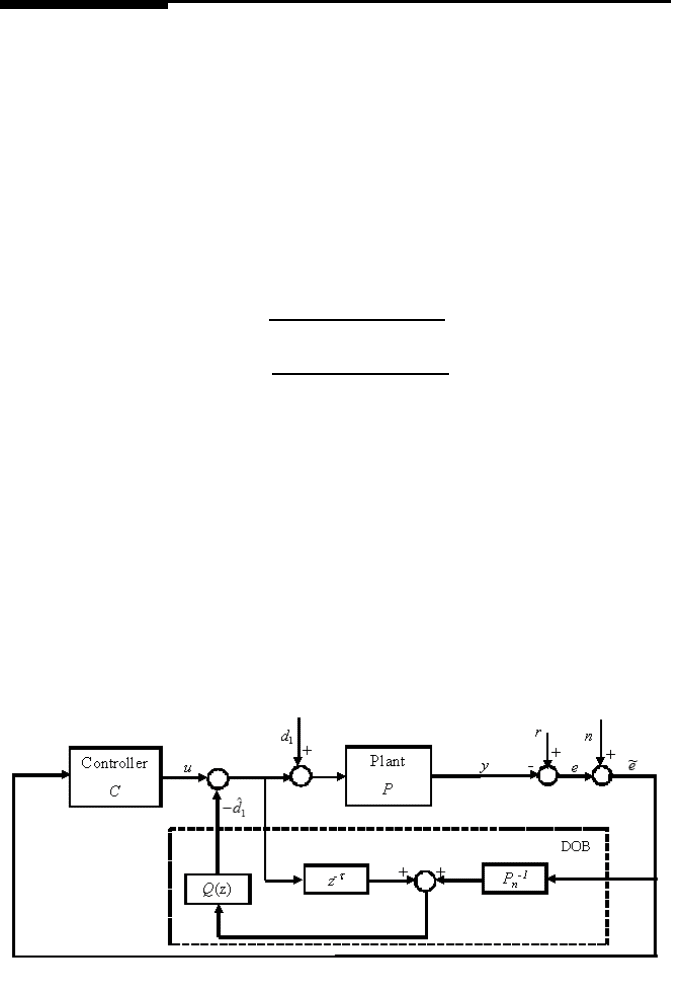
Figur e 11.1 shows the block diagram of the conventional disturbance observer (DOB)

structure, where C is the f eedback controller, P

is the nominal model of the plant

P , d

is the input disturbance, n is the noise,

is an estimate of d

, and P

−1

is the

inverse o f P

. τ represents a delay in t he plant P . Theoretically, P (z) = z

−τ

(z).

Ignoring the n ominal feedback loop with C, the transfer functions from the distur-

bance d

and noise n t o th e output y are given by

P P

(1 − Qz

−τ

)

+ Q (P − P

−τ

)

, (11 .1)

−P Q

+ Q (P − P

−τ

)

. (11.2 )

To reject the disturbance d

, Q can be set as unity because T

≈ 0 when the

delay is negligible. However, when Q = 1, T

≈ −1 which means the measure-

ment noise n is not att enu at ed. Thus, to eliminate the noise effect, it is k nown from

(11.2) that an ideal solution of Q is zero, but this will mean T

≈ P and hence the

disturbance wi ll be ampliﬁed.

FIGURE 11.1

Block diagram of the cont rol loop with a conventional disturbance observer.

∞

-Based Desig n for Disturbance Observer 217

Considering the overall system in Figure 11.1, t he sensitivity function is given by

S(z) =

1 − Qz

−τ

1 − Qz

−τ

+ P C + P QP

−1

. (11.3)

Theoretically, the plant model is P = P

−τ

, thus (11.3) becomes

S(z) =

1 − Qz

−τ

1 + P C

, (11.4)

which is stable as long as Q is stable si nce the loop is stable before the disturbance

observer is added on. Mo reover, it is dedu ced from (11.3) that when Qz

−τ

= 1 with

zero phase around th e distu rbance f requency, the disturbance can be rejected because

S(z) → 0. Hence Q is designed su ch that the ph ase of Qz

−τ

is almost zero degree

and the magnitude is close to one in the frequency range where the disturbance d

dominates. Note th at in Figure 11.1, it is needed to solve the inverse P

−1

of the

nominal plant mod el . In what follows, a general form of the di sturbance observer is

proposed and the plant model inverse is not needed.

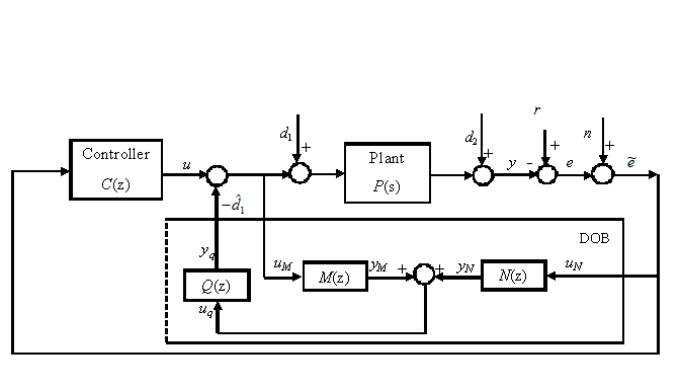
11.3 A general form of disturb ance observer

Let

(z) = B(z)/A(z), (11.5 )

B(z) = b

+ b

m−1

+ ···+ b

A(z) = z

+ a

n−1

+ ···+ a

be the nominal model of the plant P . With the same notations as in Figure 11.1,

Figur e 11.2 displays a general form of disturbance observer, where

M(z) =

B(z)

, N (z) =

A(z)

, (11.6 )

and d

is the output disturbance.

In the conventional disturbance observer in Figure 11.1,

M(z) = z

−τ

, N(z) = P

−1

(z). (11.7)

Denote the state-space descriptions P (z) : (A

, B

, C

, D

); C(z) : (A

, B

, D

); M(z) : (A

, B

, C

, D

); N(z) : (A

, B

, C

, D

). From

Figur e 11.2,

x(k + 1) = Ax(k) + B

w(k) + B

(k), (11.8)

(k) = C

x(k) + D

w(k) + D

(k), (11.9)

y(k) = C

x(k), (11.1 0)

218 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 11.2

Block diagram of the cont rol loop with a general disturbance observer.

where

A =







−B

0 0

−B

0 0

−B

0 0 A







, (11.11)







−B

0 −B







, B







−B









−D



, (11.12 )



0 −(D

+ D

) D

+ D



, D

= −D



−C

0 0 0



, D

= [0 − 1 0], D

= 0 , (11.13)

and x

(k) = [x

(k) x

(k)] is the augmented state of P (z), C(z),

M(z), and N (z), and w

(k) = [d

(k) d

(k) n(k)].

Denote the transfer function from w to y as T

= [T

]. The H

∞

optimization method will be applied to design Q(z) to minimize the H

∞

norm



∞

. (11.14)

, W

and W

are weightings. Here the models for disturbances d

, d

and

noise n are not needed. However, in order to have a desired suppression of the

∞

-Based Desig n for Disturbance Observer 219

disturbances d

, d

and the no ise n, appropriately chosen wei ghtings W

, W

and

are required which relies on our knowledge of the disturbances.

Different from the conventional disturbance observer, the general disturbance ob-

server does not need the inverse of the nominal plant model. As shown later, it is

able to suppress the disturbances in a low frequency range withou t much perfor-

mance degradation to higher frequency disturbances and noise.

The objective of the general disturbance observer design is then stat ed as: Given

a positive scalar γ and appropriate weightings W

, W

and W

, design a stable

Q(z) : (A

, B

, C

, D

) su ch that

k[W

]

∞

< γ. (11.15)

The H

∞

control design problem can be solved via Theorem 5.4.

REMARK 11.1 The sensitivity function of the control system in Figure

11.2 with the general disturbance observer is given by

S(z) =

1 + QM

1 + P C + QM − P QN

. (11.16)

With the conventional disturbance observer in (11.7), (11.16) is equal to

S(z) =

1 + Qz

−d

1 + P C + Qz

−d

−P QP

−1

. (11.17)

Assume that in (11.16)

Q(z) = Q

(z) ×

B(z)

, P = P

, (11.18 )

then

S(z) =

1 + Q

1 + P C + Q

−Q

, (11.19)

which recovers the form in (11.17) when d

≥ d

, meaning that the con-

ventional disturbance observer is a special case of the general disturbance

observer.

REMARK 11.2

In Figure 11 .2, if the loop is cut at u, the transfer function from u to ˜e or

y is considered as a new plant, and derived as

equ

1 − (M − P N )Q

. (11.20)

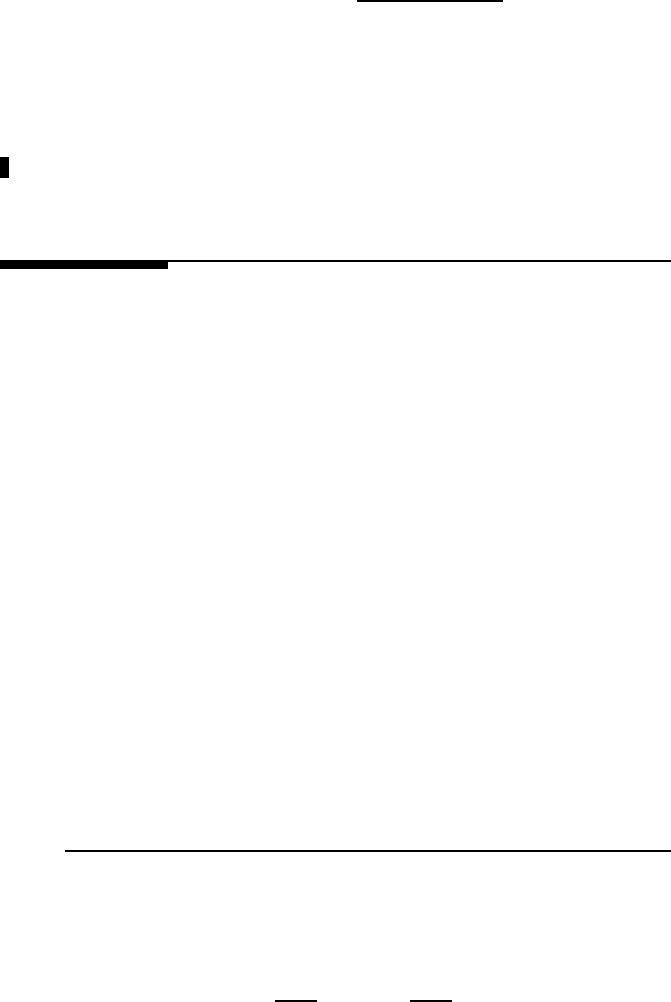
220 Modeling and Control of Vibratio n in Mechanical Systems

An equivalent open loop is denoted by T

EQ−OL

(z), and

EQ−OL

(z) = P

equ

C =

P C

1 − (M −P N )Q

. (11.2 1)

Assume ideally that P

= P and d

= d

. Equation (11.20) becomes

equ

= P , which implies that the proposed general disturbance observer does

not inﬂuence the characteristics of open-loop P (z)C(z) greatly and thus the

stabili ty and performance achieved by the nominal control loop with controller

C(z) are maintained. This i s simila r to the conventional disturbance observer.

11.4 Application results

It has been shown that a disturbance observer is capable of estimating disturbances

and modeling error [128]. Hence, disturbance observers can be used to increase the

R/W head-positioning accuracy in hard disk drives (HDDs) by using its estimation

results to cancel the effect of the disturbances and modeling error. Fu rther, due to its

cost effectiveness and easy “add-on” i mplementation with min imal change required

to the existing feedback controller, the dist urbance observer wi thout using additional

sensors is frequently used to enhance the tracking performance of a hard disk drive

servo system, such as t he attenuation of distur bances [127], and the compensation of

VCM pivot friction [130].

Consider the VCM plant with model P (s) given in C hapter 10. The discretized

model with the sampling time T

= 1/30000 sec is given by (11.5) with

B(z) = 0.02399z

+ 0.1868z

− 0.03483z

−0.02165z

+ 0.1728z + 0.02025,

(11.2 2)

A(z) = z

− 3.052z

+ 4.657z

− 4.979z

+ 3.997z

− 2.399z + 0.7765 .

(11.2 3)

The controller C(z) is the combination of a PID controller and two notch ﬁlters, and

given by

C(z) =

1.474 × 10

−5

−4.416 × 10

−5

+ 6.517 × 10

−5

− 6.621 × 10

−5

+5.015 × 10

−5

−2.872 × 10

−5

z + 9.053 × 10

−6

3.333 × 10

−5

−7.59 × 10

−5

+ 8.081 × 10

−5

−4.846 × 10

−5

+1.545 × 10

−5

−5.234 × 10

−6

(11.2 4)

Let

M(z) =

B(z)

, N (z) =

A(z)

, (11.25)

∞

-Based Desig n for Disturbance Observer 221

= 0.3, W

= 1 and W

= 1.5. A stable Q(z ) is then obtained via the H

∞

optimization in (11.14) and its frequency response is shown in Figure 1 1.3. No te

that the plant model inverse is not required in the general disturbance observer. This

beneﬁt is of great signiﬁcance, especially for nonminimum phase plant.

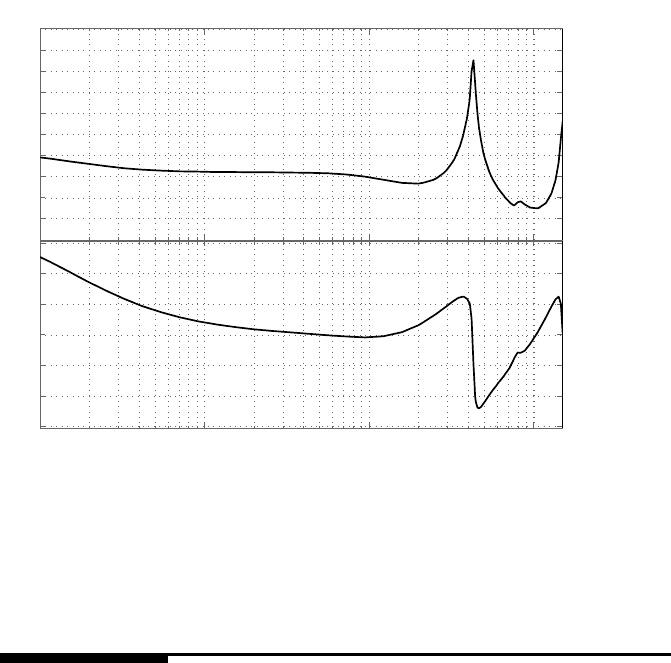
The sensitivity function |S(z)| is pl otted in Figure 11.4, from which it can be

seen that the designed disturbance observer is able to suppress disturbance with f re-

quency lower than 1 kHz witho ut causing much degradation for rej ecti on of higher

frequency disturb ance. The servo performance, such as bandwidth, will change with

different weightings W

, W

and W

. Thus by adjusting t he weightin gs accord-

ing to th e weights of d

, d

, and noise n in the position error signal, the designed

disturbance observer will result in a desired reduction rate of the error. To demon-

strate the effectiveness of the disturbance estimation in the time domain, we assume

that t he disturbances d

and d

and the noi se n are generated by d

= D

(s)w

= D

(s)w

and n = N

(s)w

, where

(s) =

0.0004(s

−83.39s + 9.741 × 10

)(s

+ 1616s + 9.626 ×10

)

+ 125.7s + 3.948 × 10

)(s

+ 10.05s + 1.011 × 10

)

(s) and N

(s) are in (2.60) and (2.61), and w

(i = 1, 2, 3) are independent white

noises with unity variance.

With t he designed general disturbance observer, the estimate

of d

is shown in

Figur e 11 .6. It follows t he original d

approximately. As a result, t he error signal is

shown in Figure 1 1.7. 50% reduction is achieved. The general disturb ance observer

is more effective to compensate for the input disturbance d

than d

and n. W

and

are selected as 1 and 1.5 is to keep the attenuation to d

and n achieved by the

nominal feedback controller C(z). With lower W

and W

and higher W

, the

attenuation to d

and n will be degraded, althoug h more suppression to d

will be

attained by using the disturbance observer.

Moreover, the conventional disturbance observer is desig ned for comparison. M(z)

and N(z) are given by

M(z) = z

−1

, (11.26)

N(z) = P

−1

(z)

5.2494(z

− 1.983z + 0.9834 )(z

−1.253z + 0 .9654)(z

+ 0.1836z + 0.817 9)

z(z + 0 .9501)(z + 0.1259)(z + 0.116)(z

− 1.22z + 0.9646)

(11.2 7)

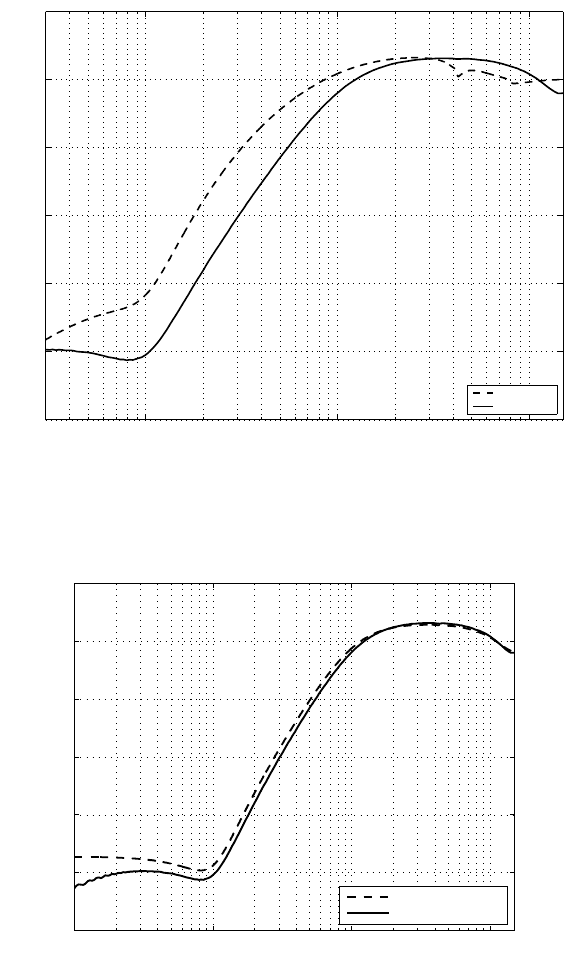
A stable Q(z) for the conventional disturbance observer is designed with the H

∞

control method . Figure 11.5 sh ows th e resultant sensitivity f unction, which is similar

to the o ne from the general disturbance observer. However, the plant model inverse

needs t o be calculated.

Experiment has been done with a LDV and a dSpace 1103. The measured sensi-

tivit y fun ct ions are shown in Fig ure 11.8, which agree with the simulation results in

Figur e 11.4. To evaluate the effect of the disturbance observer on the stabi lity and

performance achieved by the nominal controller C(z), T

EQ−OL

is measured with the

222 Modeling and Control of Vibratio n in Mechanical Systems

general d isturbance observer and the conventional disturbance observer, and shown

in Figure 11.9 and Figure 11.10. As expected, performance measures such as gain

margin and phase margin are not affected.

−10

−5

Magnitude (dB)

135

180

225

270

315

Phase (deg)

Bode Diagram

Frequency (Hz)

FIGURE 11.3

Frequency response of the designed Q(z).

11.5 Co nclusion

A general form of disturbance observer has been presented and designed based on

the H

∞

control method to achieve desir ed disturbance/noise r ejection. The distur-

bance observer does not need to solve the plant model inverse, and thus its d esign

is simpliﬁed and has great advantages over t he conventional distur bance observer,

especially for nonminimum phase plant. The simulation and implementation resul ts

show th at the general disturbance observer designed using t he method employed in

this chapter is able to effectively improve the attenuation of disturbance in low f re-

quency, and will not sacriﬁce the stability and performance of the nominal feedback

control loop.

∞

-Based Desig n for Disturbance Observer 223

−50

−40

−30

−20

−10

Magnitude(dB)

Frequency(Hz)

No DOB

With DOB

FIGURE 11.4

The sensitivity functions without and with the g eneral disturbance observer.

−50

−40

−30

−20

−10

Magnitude(dB)

Frequency(Hz)

Conventional DOB

General DOB

FIGURE 11.5

The sensitivity function comparison with the general and the conventional distur-

bance observers.