Du C., Xie L. Modeling and Control of Vibration in Mechanical Systems

Подождите немного. Документ загружается.

244 Modeling and Control of Vibratio n in Mechanical Systems

control in time di mension.

As is known that one of the most important performance measures for SSTW is

the track misregistration or TMR, the total amount of random ﬂuctuation about the

desired track location. TMR is used to judge the required accuracy of posi tioning. To

achieve a hig h posi tioning accuracy, one way in servo control is to minimize TMR,

which is expressed as the standard deviation of the true PES, i.e.

y(i,j)

K − 1

L,K−1

i,j=0

y(i, j)

. (12.55 )

Let T

: w → y denote the closed-loo p system subject to a whit e noise w. When

L and K are large enough, the H

norm of T

can be approximately given by

K − 1

L,K−1

i, j=1

y(i, j)

. (12.56)

Thus, the control design problem to minimize TMR can be treated as a 2-D H

optimal control problem, which is stated as follows: ﬁnd a 2-D ou tput feedback

controller of th e form in (12.9)−(12.10) for the SSTW plant P (s) such th at the

closed-loo p system is stabl e and the H

performance kT

is minimized.

The problem of minimizing the TMR of the SSTW process is thus formulated as

the 2-D H

control pro blem. A 2-D H

controller wi ll subsequently be design ed to

minimize the track mis-registrati on. Note that since the 2-D controller stabilizes the

system, it also contains the error propagation. Thus, the 2-D H

control approach

simultaneously addresses the error pr opagation and TMR minimization prob lems,

which is different from the previous 1-D method where the problems are addressed

separately b y feedback and feedforward controls.

12.7 2 -D stabilization control for error propagation containment

12.7.1 Simulation results

The simulation block diagram on 2-D control is shown in Figure 1 2.14. The sim-

ulation is carried out in MATLAB/Si mulink. I n the simulation , the sector number

K = 270, the spindle rotational speed is 7200 RPM, and thus the sampling fre-

quency i s 270 × (7200/60) = 32400 Hz.

To show the capability of the designed 2-D controller to prevent the error propa-

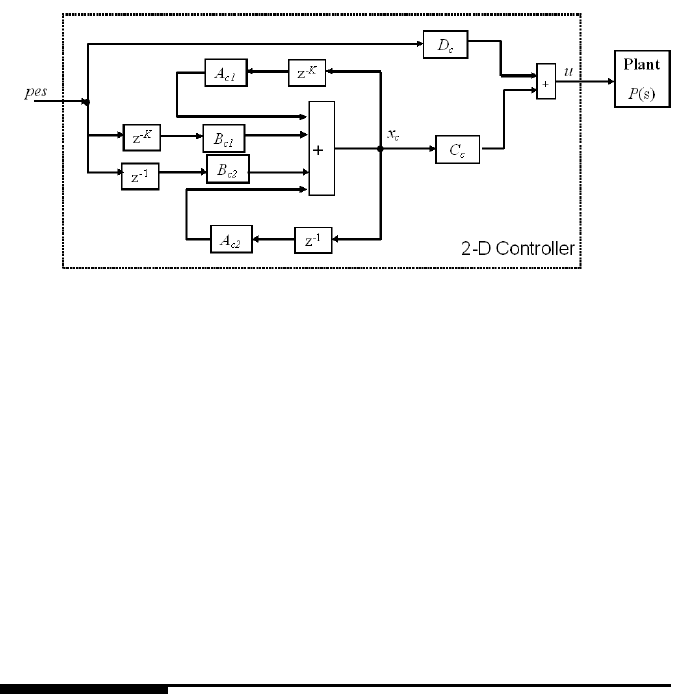
gation, 100 tracks are propagated in the simulation. The results show that the SSTW

process is stabi lized and the error propagation is contained. The σ value of PES

NRRO is plotted versus the track number in Figure 12.15, which implies that the

error amplitude is oscillating steadily.

Two-D imensional H

Control for Error Minimization 245

FIGURE 12.14

2-D controller for SSTW servo loop.

From (12.9)−(12.10) and Figure 12.14, it is not di fﬁcult to see that (A

, B

, D

) is acting along the time directi on only, and thus actually it works like the

1-D controller we usually take into account. Su bsequently, the open-loop and the

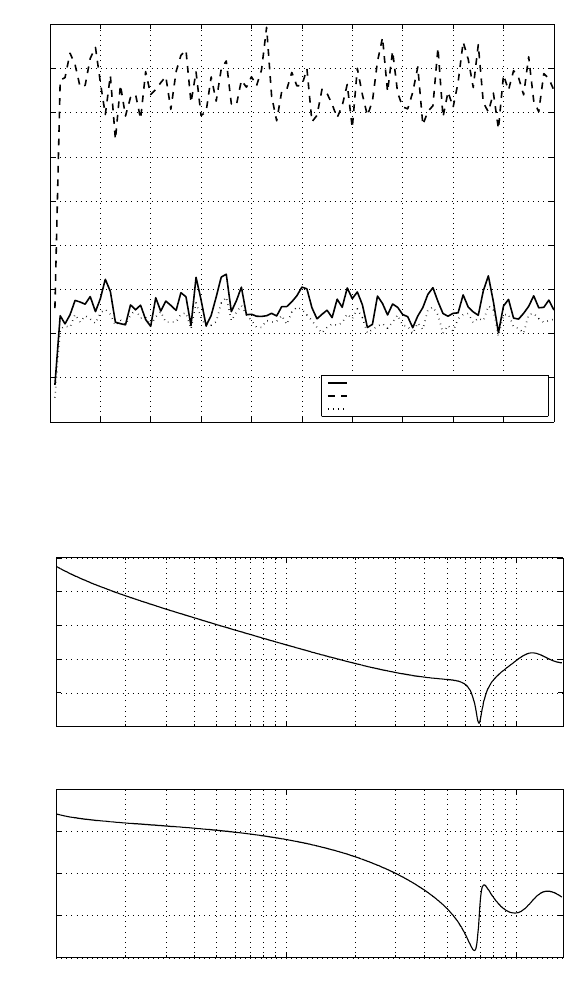
sensitivit y function frequency responses are obtained and shown in Figures 12.16

and 12.17. The open-loop crossover frequency is 1.6 kHz, the gain margin is 6 dB,

and the phase margin is 50 degrees. A bad high frequency part of the sensitivity

function has appeared, because here only the stabilization problem i s con sidered and

no performance optimization is involved. Thus the 2-D H

control will be presented

which gives a better performance t han the stabilizing only controller.

12.8 2 -D H

control for error minimizatio n

12.8.1 Simulation results

The σ value of PES NRRO is plotted versus the track number in Figure 12.15, where

the error amplitude is oscill at ing steadily, which implies that error pro pagation is

contained. Additionally, the position error has been minimized in the H

norm sense.

The σ values of PES NRRO with the stabilization control and the H

control are

compared in Figure 12.15 and it is seen that the erro r is reduced by an average of

60% via the 2-D H

control.

The conventional 1-D H

feedback control has al so been designed to minimize

the error sign al, and based on the f eedback control a feedforward control is further

designed to contain the error propagation. This method is also compared with the

above two methods in Figure 12.15. It is seen that the proposed 2-D control method

is comparable to the previous 1-D control metho d.

246 Modeling and Control of Vibratio n in Mechanical Systems

0 10 20 30 40 50 60 70 80 90 100

x 10

−3

Track number

σ of pes NRRO (µm)

2−D H2 control

2−D Stabiliation

1−D H2 feedback+feedforward control

FIGURE 12.15

σ of PES NRRO versus track number.

−20

−10

Magnitude(dB)

−250

−200

−150

−100

−50

Phase(deg)

Frequency(Hz)

FIGURE 12.16

Open-loop frequency response with stabil ization controller.

Two-D imensional H

Control for Error Minimization 247

−30

−25

−20

−15

−10

−5

Magnitude(dB)

Frequency(Hz)

FIGURE 12.17

Sensitivity function with stabilizatio n controller (A

, B

, C

, D

12.8.2 Experimental results

It is noted that in th e 2-D controller (12.9)−(12.10), (A

, B

, C

, D

) acts in

the time dimension, and ru ns on the same track as a 1-D controller C(z) we have

usually considered. Thus in this section we particularly take into account the 1-D

controller C(z) : (A

, B

, C

, D

) for the p lant P (s) (12.38)−(12.40) in the

time dimension.

Straigh tforwardly from the desig ned 2-D controller C(z

, z

) : (A

, A

, B

, C

, D

), the 1-D controller C(z) : (A

, B

, C

, D

) can be obtained

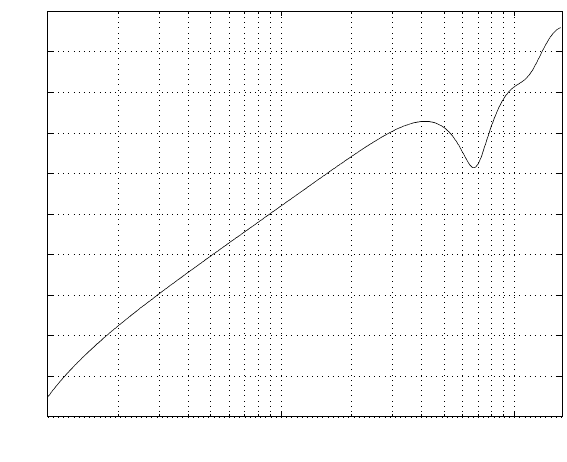
and its frequency response is shown in Figure 12.18, where the no tches aroun d 4, 6

and 9 kHz are to su ppress the resonances as observed in Figure 12.6. With the 1-D

controller C(z), the simulated frequency responses of th e op en loop C(z)P (z) and

the sensitivity function S(z) = 1/(1 + C(z)P (z)) are drawn i n Figures 12.19 and

12.20.

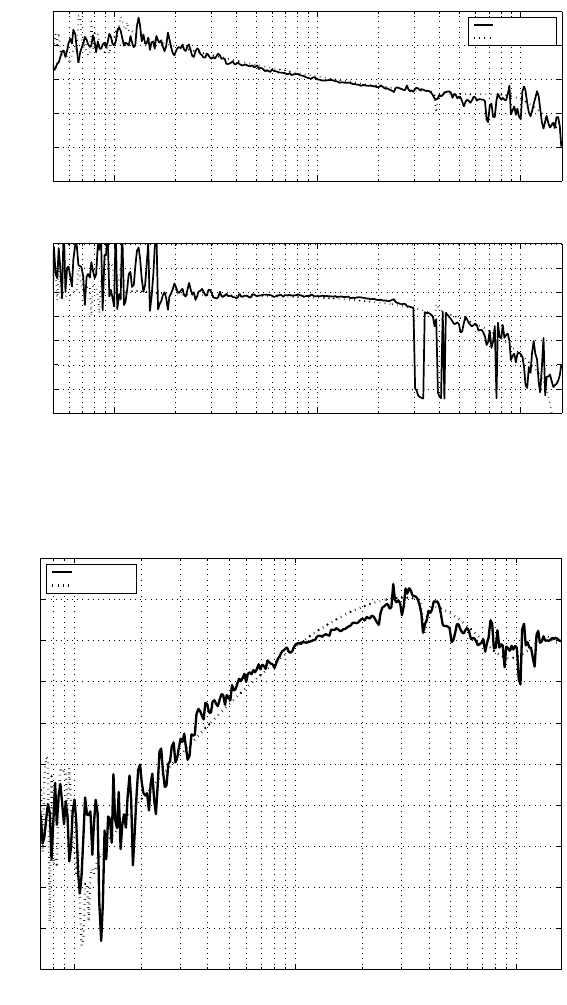
To practically verify the 1-D contr oller C(z), experiment is carried out with dSpace

1103 on TMS320C240 DSP board and the LDV used to measure the displacement of

the actuator. The measured open-loop frequency response compared with the simu-

lated one is shown in Figu re 12.19, and the crossover frequ ency is 1.2 kHz, the gain

margin is 9 dB, and the phase margin is 54 degrees. Figure 12.20 also shows the

measured sensitivity funct ion with comparison to the simulated one. Additi onally,

the step respon se and the control signal of the closed loop are taken from the oscillo-

248 Modeling and Control of Vibratio n in Mechanical Systems

scope as a bmp picture shown i n Figure 12.21, which testiﬁes that the 1-D cont roller

drawn from the designed 2-D controller works well.

The results in this section show that the 1-D controller C(z) extracted from the 2-

D controller can stabilize the plant P (s) in the time dimension. However, as shown

in Figure 12.3, one 1-D feedback controller C(z) is not capable enough to contain

error propagation and stabi lize the SSTW process modeled in (12.30)−(12.37) in

two dimensions. On the basis of the 2-D model, the designed 2-D controller can

stabil ize the SSTW process and minimize the position error simultaneously.

Bode Diagram

Frequency (Hz)

Phase (deg) Magnitude (dB)

−30

−20

−10

−90

−45

135

FIGURE 12.18

Frequency response of controller (A

, B

, C

, D

12.9 Co nclusion

This chapter has employed 2-D controllers in stabi lization and error minimization

of systems that have 2-D behavior and can be modeled as a 2-D model. The ap-

plication in a self-servo track writing process described by a 2-D model has been

addressed in detail. By applyin g the two-dimension al model, the error propagation

Two-D imensional H

Control for Error Minimization 249

−60

−40

−20

Magnitude(dB)

Measured

Simulated

−600

−500

−400

−300

−200

−100

100

Phase(deg)

Frequency(Hz)

FIGURE 12.19

Open-loop frequency response with controller (A

, B

, C

, D

−40

−35

−30

−25

−20

−15

−10

−5

Frequency(Hz)

Magnitude(dB)

Measured

Simulated

FIGURE 12.20

Sensitivity function with controller (A

, B

, C

, D

250 Modeling and Control of Vibratio n in Mechanical Systems

FIGURE 12.21

Step response (Channel 1/2/3: Reference/Out put/Control signal).

containment problem and the TMR minimization problem o f the self-servo track

writing process has been formulated as a 2 -D H

control problem. With the stored

error information of the preceding track, the adopted 2-D controller is applicable.

The 2- D approach provides a systematic way of achieving both the error propagation

containment and the TMR minimizati on simultaneously. The simulation results have

demonstrated that the error propagation is prevented by t he 2-D control scheme, and

good positioning accuracy is achi eved with the 2-D H

control scheme. Also, the

time dimension al portion, as a 1-D controller, of the designed 2-D controller has

been implemented via LDV and dSpace and t he implementation results have been

shown to verify that the 1-D con troller performs well.

Nonlinearity Compensation and N onlinear

Control

13.1 Introduction

Nonlinearities such as friction in the actuator pivot are known to limit the low fre-

quency gain of a control loo p. Translated to the error rejection function or sensitivity

function, it lifts the magnit ude of the sensitivity function at low frequencies, and

thus reduces the abilit y of the control loop to reject vibrations at low frequencies and

affects the system performance. Based on an identiﬁed friction model, the friction

can be compensated for by injecting an estimated friction force into the actuator. A

friction compensation method based on a nonlinear hysteresis model is thus studied.

Moreover, on the basis of a linear feedback control, to further improve the re-

jection of low-frequency disturbances such as nonlinear disturbances arising from

friction to rque o r bias or other unknown disturbances, an adaptive nonlinear com-

pensation scheme wil l be adopted in this chapter to cancel their effects through a

proper estimation of the disturbances.

13.2 No nlinearity compensation

As stated in Chapter 2, the nonlinear friction model f

= F (x(k)) is identiﬁed as

in the form of (2.20) using the operator based method. With the model, the friction

can be compensated for by injecti ng the friction force f

into the plant, as seen in

Figur e 13.1. A sinusoidal signal of 50 Hz and 1 V amplitude is injected as the

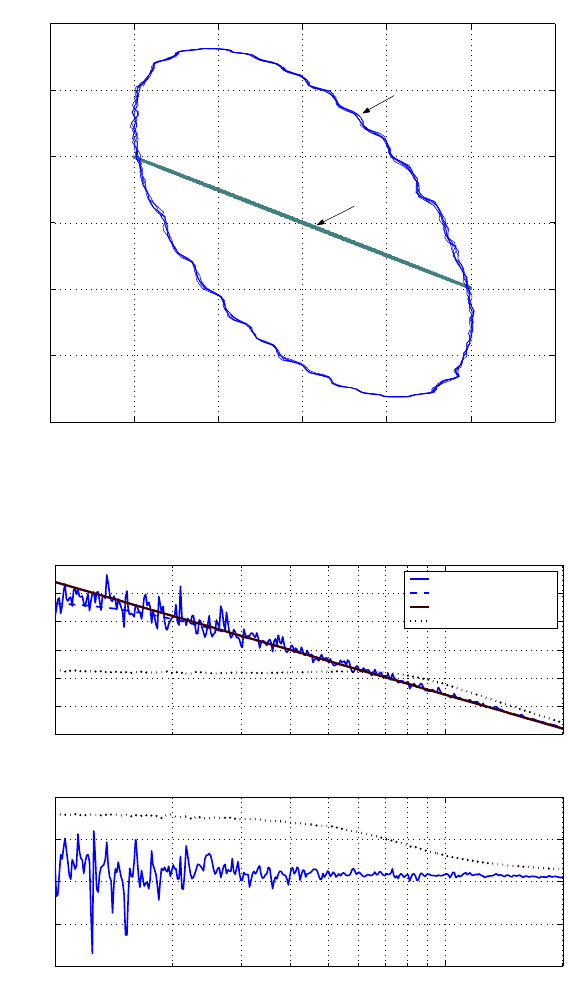
reference. The input u versus the actuator displacement x is compared for the cases

of with and without the nonlinear compensation in Figure 13.2. It is evident that

with the no nlinear compensation the relationship between u and x is linearized very

well. In the fr equency domain, the actuator frequency responses before and after the

compensation are measured with a swept sine wave via a DSA and shown in Fi gure

13.3. The compensated magnitude and phase responses approach those of the pure

double integrator much more closely than those before compensation.

With the friction compensation, the VCM actuator frequency respon ses are mea-

251

252 Modeling and Control of Vibratio n in Mechanical Systems

sured with different sinusoidal reference amplitudes and plotted in Figures 13.4 and

13.5, where the straight smooth lines are from the pure double integrator. It is seen

that the linearization effect becomes b etter wh en the reference amplitude is higher

than 1 V (0.5 µm/V), and it is not so satisfactory for 0 .25 V. Although the friction

model is obtained on the basis of the measurement for 0.5, 1, and 3 V displacement

amplitudes, the compensation based on the obtained model is able to achieve good

linearization effect for any displacement ranging from 0.5 V and above.

FIGURE 13.1

Fricti on compensation for the actuation system.

Figur e 13.6 shows the correspond ing simulated and measured sensitivity func-

tions. With the compensation the magnitude at 10 Hz is reduced by around 20 dB

due to the increased open-loop gai n at low frequencies as seen in Figures 13.4 and

13.5. The slightly lower magnitude fro m 60 to 100 Hz before compensation, corre-

sponding to the hi gher magnitu de of the original actuator model from 60 to 100 Hz

in Figure 13.3, is caused by the nonlinearity of the origi nal actuator.

In the above, a model based nonlinearity compensation has improved the ability of

the closed control l oop to reject vibrations in low frequency range. In the rest of the

chapter, a non-model based compensation, which is an adaptive and a more ﬂexible

scheme, will be applied to compensate the nonlinear or unknown vi brations in low

frequency range.

13.3 No nlinear cont rol

While a KYP Lemma-based linear control can achieve disturbance rej ecti on over

some chosen frequency ranges, it cannot run away from performance limitation,

Nonlinearity Comp ensation and Nonlinear Control 253

−1.5 −1 −0.5 0 0.5 1 1.5

−1.5

−1

−0.5

0.5

1.5

x 10

−3

Displacement (V, 0.5 µm/V)

Input u (V)

No compensation

With compensation

FIGURE 13.2

Input u versus displacement x with and wi thout compensation .

100

After comp.(measured)

After comp.(simulated)

1/s

Before comp.

−400

−300

−200

−100

Frequency(Hz)

Phase (deg)

Magnitude(dB)

FIGURE 13.3

Actuator f requency responses with and without friction compensation.