Доспехов Б.А. Методика полевого опыта

Подождите немного. Документ загружается.

г) групповые или частные средние

для каждого значения

по фор-

муле

/^i

где Ау=18\ 1^=5;

д) значения х, у, И(Х~х), 2 (У—у) и

(Х~х) (Y—y)

исходных едини-

цах, записывая их под таблицей 97. Следует иметь в виду, что если в процессе

кодирования производилось деление или умножение на

и i

, то суммы квад-

ратов

первом случае надо умножить,

во втором разделить на i

или и/;

сумму произведений отклонений в первом случае надо умножить,

во втором

разделить на

Вычисляют выборочный коэффициент корреляции, регрессии и уравне-

ние регрессии

по X:

Z(X-7)(Y~y)

51,13

0,67;

1/"S(X

—

х)

2(К

—]/)

]/2,46X2348,5

2(Х—I) (7

— 7)

51,13

__i

Ll_—»>__

—

20,8 мг;

ух

2(Х~х)

2,46

=~у~-\-

й^(Х —7)

20,3 +• 20,8

(X —

1,32)

20,8Х

—

7,2.

Определяют ошибки, критерий значимости, доверительные интервалы

для г и Ь

ух

и проверяют Я

l/ l—/"

l/l

—0,67

Л лп

= ]/-^ГГ=У 64-2 =

°>°94;

лЛ^

=0,094

l/-

* V 2(Х~ *)»

' |/

2348,5

= ^ \/ ^;

=0,094

246

2,9мг;

уж

Уъ (Y

—

у)*

0,094 "J/2348,5

4,61 мг;

0,67

''"-"

— 0,094

—

7,13;

n=64— 2=62;

О6

=2,00;

г ±(

=0,67 ±2,00X0,094 =0,67 ±0,19 (0,49

-т-

0,86);

ух

±io

=20,8

2,00x2,9 =20,8 ±5,8 (15,0

26,6) мг;

отвергается (/ф^>/

б)-

По найденному уравнению регрессии рассчитывают средние теоретиче-

ские значения

для экстремальных групповых значений

и строят теорети-

ческую линию регрессии

по X:

1/*=о,85

20,8x0,85 -7,2= 10,5;

1/х=1,б4

20,8X1,64-7,2= 26,9 мг.

Построив на графике точки

(0,85;

10,5)

(1,64; 26,9), проводят через них

теоретическую линию регрессии У по X (рис. 51); пунктирными линиями ука-

зывают доверительную зону регрессии для

68%

-кого

уровня.

283

у = 20,8а:-7,2

ух

-20,8

±2,3

=0,67 ±0.09

ш ®

CV,

\20

с?

1,2

Гумус, %

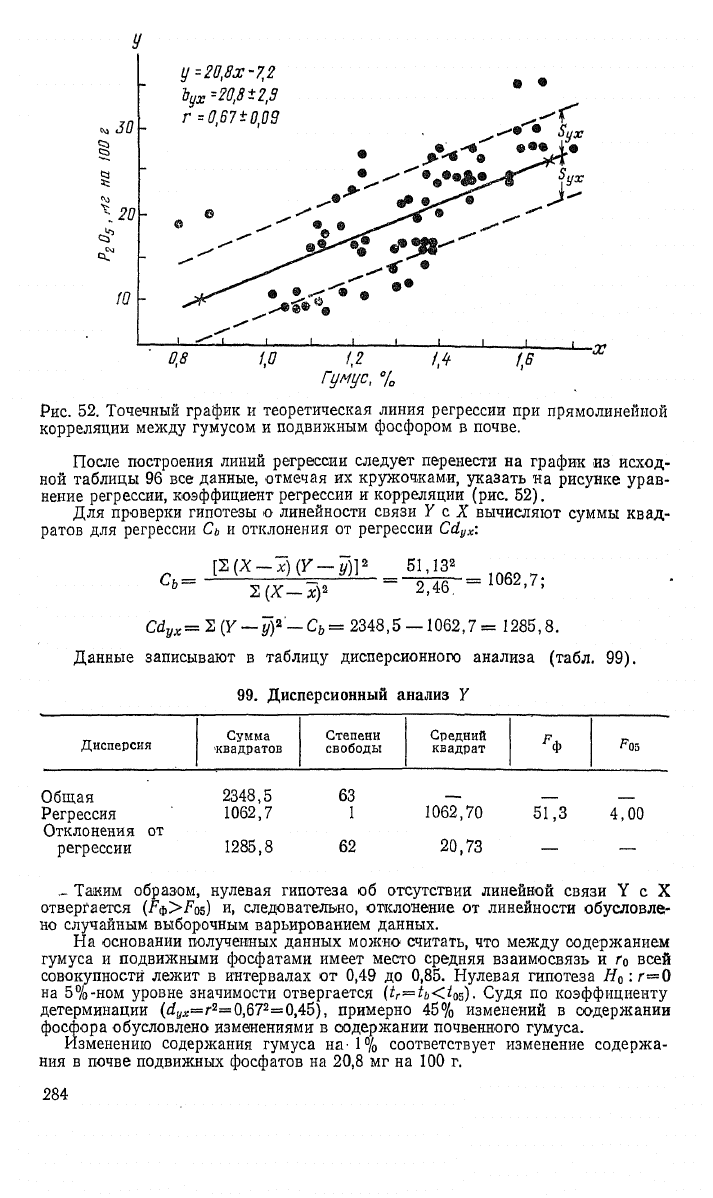
Рис.

52. Точечный график и теоретическая линия регрессии при прямолинейной

корреляции между гумусом и подвижным фосфором в почве.

После построения линий регрессии следует перенести на график из исход-

ной таблицы 96 все данные, отмечая их кружочками, указать на рисунке урав-

нение регрессии, коэффициент регрессии и корреляции (рис. 52).

Для проверки гипотезы о линейности связи У с X вычисляют суммы квад-

ратов для регрессии Сь и отклонения от регрессии

[Ъ(Х-х)(У~у)]*

51,13

-Оё-= Ю62,7;

2 (Х-л)

='Z(Y~y)

'—C

= 2348,5 —1062,7= 1285,8.

Данные записывают в таблицу дисперсионного анализа (табл. 99).

99.

Дисперсионный анализ У

Дисперсия

Сумма

•квадратов

Степени

свободы

Средний

квадрат

FQ5

Общая

Регрессия

Отклонения от

регрессии

2348,5

1062,7

1285,8

—.

1062,70

20,73

51,3 4,00

._ Таким образом, нулевая гипотеза об отсутствии линейной связи Y с X

отвергается (^>i

os) и, следовательно, отклонение от линейности обусловле:-

но случайным выборочным варьированием данных.

На основании полученных данных можно считать, что между содержанием

гумуса и подвижными фосфатами имеет место средняя взаимосвязь и г о всей

совокупности лежит в интервалах от 0,49 до 0,85. Нулевая гипотеза Я

: г—О

на 5%-ном уровне значимости отвергается (t

). Судя по коэффициенту

детерминации (i^=r

=0,67

=0,45), примерно 45% изменений в содержании

фосфора обусловлено изменениями в содержании почвенного гумуса.

Изменению содержания гумуса на-1% соответствует изменение содержа-

ния в почве подвижных фосфатов на 20,8 мг на 100 г.

284

По уравнению Y=20,8X—7,2 для любых значений X, включая те, которых

нет в исходных данных, молено рассчитать значение У. Однако нельзя исполь-

зовать уравнение регрессии для интерполяция за пределы таблицы.

2. ЧАСТНАЯ И МНОЖЕСТВЕННАЯ ЛИНЕЙНЫЕ КОРРЕЛЯЦИИ И РЕГРЕССИИ

Корреляция

называется

множественной,

если на величину ре-

зультативного

признака

одновременно влияют несколько

факто-

риалъных. Простой формой множественной связи является ли-

нейная зависимость между тремя признаками, когда один из них,

например урожай, рассматривается как функция (У), а два дру-

гие—

как аргументы (X и Z). В качестве меры тесноты линей-

ной связи трех признаков используют частные коэффициенты

корреляции, обозначаемые г

ху

, г

хг

fzy-x,

и множественные ко-

эффициенты корреляции, обозначаемые JR

Rz-xy.

Частный коэффициент корреляции

—

это показа-

тель,

измеряющий степень сопряженности двух признаков.

Математическая статистика .позволяет установить корреля-

цию между двумя признаками при постоянном значении третье-

го,

не ставя специального эксперимента, а используя парные ко-

эффициенты корреляции r

, r

и r

. Частные коэффициенты

корреляции рассчитывают по формулам:

ху —

xz'

xz—

xy'

VV-r\

)(l-r%

)

! xz

V(l-r%)(l~-r%) *

—

У*

ГхУ

Гхг

У(1-Г"«)(1-/*Й) '

Здесь в индексах буквы перед точкой указывают, между ка-

кими признаками изучается зависимость, а буква после точки

—

влияние какого признака исключается (элиминируется). Ошиб-

ку и критерий значимости частной корреляции определяют по

тем же формулам, что и парной корреляции:

- У п_2 ' "

~Тг '

Теоретические значения t берут из таблицы 1 приложений.

Подобно парным коэффициентам корреляции частные коэф-

фициенты могут принимать значения, заключенные между —1 ш

Частные коэффициенты детерминации находят путем возве-

дения в квадрат частных коэффициентов корреляции:

= /"

" И — /"

* И = /

"'xyz

' xyzi ^xz'y ' xz'y> ^yz-x ' yz'%'

Определение степени частного воздействия отдельных пере-

менных на результативный признак при исключении (элимини-

ровании) связи его с другими признаками, искажающими эту

корреляцию, часто представляет большой интерес. Например,

тесноту связи урожаев с осадками может сильно искажать варь-

ирование температуры, и поэтому целесообразно изучить связь

между первыми двумя признаками при постоянных значениях

третьего. С чисто внешней стороны (а не внутренней) при по-

285

"стоянном значении элиминируемого признака нельзя подметить

его статистического влияния на изменчивость других признаков.

Чтобы уяснить технику расчета и смысл частного коэффици-

ента корреляции, рассмотрим данные по определению парной

-корреляции между окружностями початка кукурузы (X), окруж-

ностью его стержня (У) и количеством рядков зерен (Z) на ос-

новании измерения 9000 початков:

яг/

= 0,799; r

= 0,570; ^ = 0,507.

По приведенным выше соотношениям определим частные ко-

эффициенты корреляции:

0,799 — 0,570x0,507

„

оп

г „,.._ = —. = 0,7zU;

xyz

>^(1 —0,570

) (1 —0.507

)

0,570 — 0,799x0,507 _« gig.

У(1 —0,799

)(1 — 0,507

)

0,507 — 0,799x0,570

xz-y

= 0,105.

У*'*

у (у _0,799

) (1 — 0.570

)

Частный коэффициент корреляции между окружностью по-

-чатка и его стержня у початков с одинаковым числом рядков

зерен {r

.z=0,720) показывает, что лишь незначительная часть

•взаимосвязи этих признаков в общей корреляции {г

ху

= 0,799)

•обусловлена влиянием третьего признака. Аналогичное заключе-

ние необходимо сделать и в отношении частного коэффициента

корреляции между окружностью початка и количеством рядков

зерен у початков с одинаковой окружностью стержня

0,318

и г

Х2

=0,57). Напротив, частный коэффициент корреля-

ции между окружностью стержня и количеством .рядков зерен у

початков с одинаковой окружностью r^.^ 0,105 значительно от-

личается от общего коэффициента корреляции г

уг

~0,507; из это-

го видно, что если подобрать початки с одинаковой окруж-

ностью, то связь между этими признаками у них будет очень

•слабой, так как значительная часть в этой взаимосвязи обуслов-

лена варьированием окружности початка.

При некоторых обстоятельствах частный коэффициент корре-

ляции может оказаться противоположным по знаку парному.

Например, при изучении взаимосвязи между морфологическими

признаками стеблей льна

—

массой (X), длиной (У) и диамет-

ром (Z)—были получены следующие коэффициенты (л=100):

между массой и длиной г

ху

0,6;

между массой и диаметром

0,9;

между длиной и диаметром r

=0,4-

Частные коэффициенты корреляции при исключении влияния

третьего признака:

0,6-0,9x0,4 .

/(1—0,9

)(1

—

0,4

)

0.9—0,6x0.4

/(1 -0,6

) (1 —0,42)

0,4

—

0,6x0,9

г~;= ... ..Г.. "I... =0.90;

]/(1 — 0,6

)(1 —0,9

)

= —0,40.

•286

Частные коэффициенты корреляции между массой

длиной

и массой

диаметром

при

статистическом исключении влияния

третьего признака

не

вызывают никаких недоумений,. Выявилась

очень высокая частная корреляция массы

диаметра

при ис-

ключении влияния длины стебля г

хг

средняя корреляция

между массой

длиной

для

растений

одинаковым диа-

метром. Частная корреляция между длиной стебля

при

посто-

янном значении массы получилась отрицательной:

при

увели-

чении длины диаметр стебля уменьшается, тогда

как

общий

ко-

эффициент корреляции указывает

на

положительную взаимо-

связь между этими признаками.

На

первый взгляд этот резуль-

тат кажется невероятным,

он

противоречит обычным представ-

лениям

росте растений: если увеличивается высота,

то,

конеч-

но,

увеличивается

диаметр стебля. Однако

это

мнимое проти-

воречие объясняется основным условием частной корреляции

—

постоянством исключаемого признака. Если взять стебли льна

одной

и той же

массы,

то

среди таких стеблей увеличение дли-

ны может происходить только

за

счет уменьшения диаметра.

При увеличении обоих признаков

не

могла

бы

оставаться

по-

стоянной масса стебля.

Метод частной корреляции дает возможность вычислить

частный коэффициент корреляции второго порядка. Этот коэф-

фициент указывает

на

взаимосвязь между первым

вторым

признаком

при

постоянном значении третьего

четвертого.

Оп-

ределение частного коэффициента второго порядка ведут

на ос-

новании частных коэффициентов первого порядка

по

формуле:

xy-v ~~

xz-v'

yz-v

*v™ -/{\-r\

){\-r*

yг

)

где

y-v,

.y — частные коэффициенты первого порядка, значение кото-

рых определяют

по

формуле частного коэффициента, используя коэффициенты

парной корреляции

xv>

, r

Множественный коэффициент корреляции

трех переменных

— это

показатель тесноты линейной свя-

зи между одним

из

признаков (буква индекса перед точкой)

совокупностью двух других признаков (буква индекса перед точ-

кой)

совокупностью двух других признаков (буквы индекса

после точки):

к,

х.

•xz~

ху~

-V-

•V-

ху

Г*

ху

+ Г*

иг

г2

х2

-Ь

уг

—

•

xyfxz

ху

Эти формулы позволяют легко вычислить множественные

ко-

эффициенты корреляции

при

известных значениях коэффициен-

тов парной корреляции

, г

хг

уг

287

Коэффициент R не отрицателен и всегда находится е преде-

лах от 0 до 1. При приближении R к единице степень линейной

-связи трех признаков увеличивается. Между коэффициентом

множественной корреляции, например

и двумя коэффици-

ентами парной корреляции г

ух

и г

уг

существует следующее 'соот-

ношение:

каждый из тарных коэффициентов не -может превы-

шать по абсолютной величине

Квадрат коэффициента множественной корреляции R

назы-

вается коэффициентом множественной детерминации. Он пока-

зывает долю вариации зависимой переменной под воздействием

изучаемых факторов.

Значимость множественной корреляции оценивается по

^-критерию:

—Я

\ k—i )•

где п — объем выборки; k — число признаков; в нашем случае

fe=3.

Теоретическое значение ^-критерия берут из таблицы 2 при-

ложений для vi—k—1 и У2=п—k степеней свободы и принятого

уровня значимости. Нулевая гипотеза о равенстве множествен-

ного коэффициента корреляции в совокупности нулю (H

\R = 0)

принимается, если /^«CC-FT, и отвергается, если

F^^F?.

Приведем пример вычисления коэффициента множественной корреляции.

При изучении методики селекционного отбора у репчатого лука второго года

жизни были получены такие коэффициенты парной корреляции (/г=15):

между урожаем (У) и средней массой луковицы (X) ... /v*=0,6;

между урожаем (У) и гнездностыо (Z) ... г

ул

=0,3;

между средней массой луковицы (X) и гнездностью (Z) ... r

=—0,2.

Необходимо выяснить зависимость урожая (У) от средней массы лукови-

цы (X) и гнездности (Z), т. е. рассчитать коэффициент множественной кор-

реляции:

-I/М

+ 0,З

-2X0,6X0,ЗХ(~~0,2)

Кухг — у

—

0,2

=и,/4.

0,74

/ 15—

' ' 7,33.

1 —0,742

(^)-

Табличное значение F при 2 и 15—3=12 степенях свободы i

5=3,89 и

~=6,93.

Таким образом взаимосвязь между урожаем, средней массой луковицы

и гнездностью Ry.

=0,74: значима на

1%-ном

уровне

F$>F

Судя по

коэффициенту множественной детерминации (i?

=0,74

=0,55), вариация уро-

жайности лука на 55% связана с действием изучаемых факторов — средней

массой луковицы и гнездностью и 45% вариации (1—JR

) не может быть

объяснено влиянием этих переменных.

Математическое уравнение для прямолинейной зависимости

между тремя переменными называется множественным линей-

ным уравнением плоскости регрессии. Оно имеет следующий об-

щий вид:

Y = a+b

X-\-b

тде У—зависимая переменная, X и Z

—

независимые переменные, а — общее

•начало отсчета, Ь

— коэффициенты частной регрессии. Коэффициент Ь±

288

показывает, на какую величину увеличивается У при каждом увеличении на

одну единицу X при постоянном значении Z; коэффициент Ь

указывает, на

какую величину увеличивается У при увеличении Z на единицу при постоянном

значении X. Поэтому часто используют обозначения bi=b

Ь<ь=Ь

у2

.х,

при-

нятые для частных коэффициентов корреляции.

Параметры а,

и Ь

вычисляют методом наименьших квад-

ратов, который позволяет найти такое положение плоскости ре-

грессии в пространстве, когда сумма квадратов отклонений эм-

пирических точек от нее является минимальной:

2 [К—

(а~|ЛХ-)-ВД]

мин.

Для определения параметров уравнения используют соотно-

шения:

1-4

2(X—x)

2(Z

—

2)2—[2

— x)(Z— z)f

(*-*)

<У-y)_(z-7)-2(x-x)(z-ijs(X-I)(y-y)

2(X —x)

2(Z —

— [2(X

— x)(Z

—

2)]

= r/—b

x—b

Установленное уравнением регрессии отношение зависимости

коррелируемых признаков принято изображать графически в

виде линий и поверхности регрессии.

Рассмотрим следующий схематизированный (для наглядности) пример.

Сопряженность урожайности соломы льна-долгунца У (ц с 1 га) с дозой удоб-

рений X (ц на 1 га) и осадками июня Z (мм) близка к линейной и выражается

таким уравнением (в интервале доз от 0 до 6 и осадков от 60 до 120):

y=lO + 3X + 0,25Z.

Подставляя в уравнение значения доз, например 0, 2, 4 и 6, для зафикси-

рованного количества осадков, например 60, 80, 100 и 120, получим коорди-

наты точек для построения линий и плоскости регрессии (табл. 100).

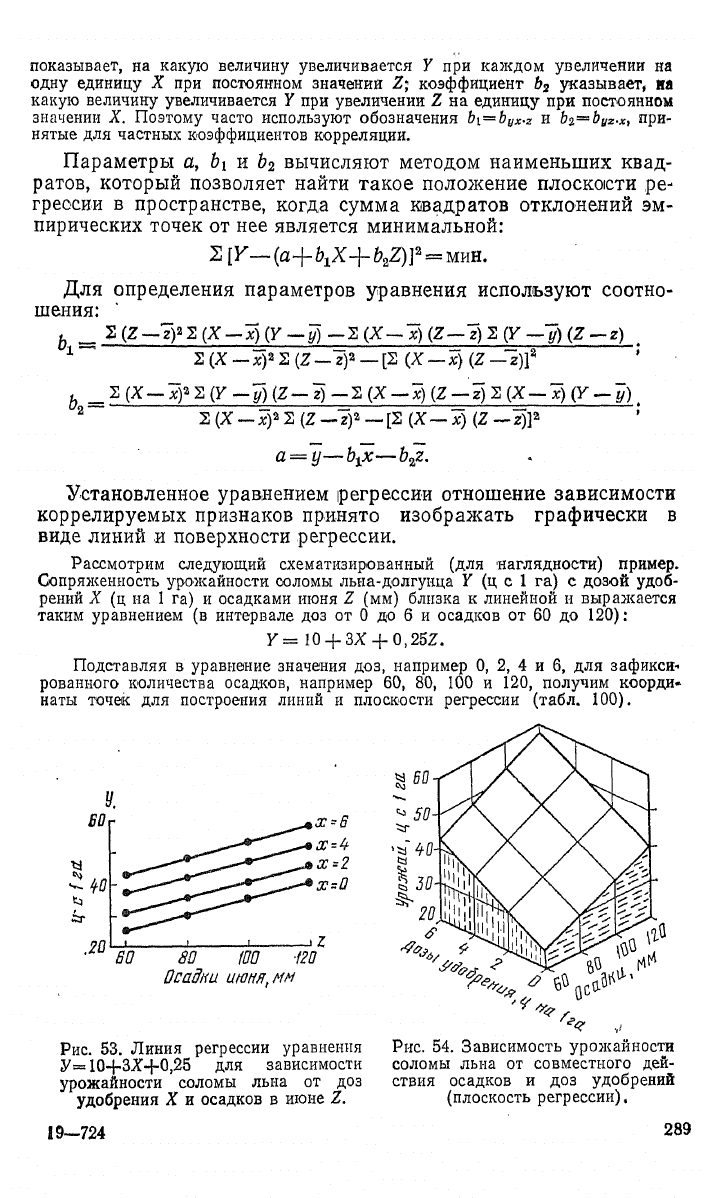
Рис.

53. Линия регрессии уравнения Рис. 54. Зависимость урожайности

у= 10+3X4-0,25 для зависимости соломы льна от совместного дей-

урожайности соломы льна от доз ствия осадков и доз удобрений

удобрения X и осадков в июне Z. (плоскость регрессии).

19—724

289

100.

Урожайность соломы льна (ц с 1 га), рассчитанная

по уравнению Y=lO + 3X+0,2bZ

(ц на 1 га)

Осадки Z (в мм)

60 80

100 120

На рисунке 53, по данным таблицы 100, построены линии регрессии У на

Z для четырех фиксированных значений X. Кружками показаны точки (У;

Z) соответственно четырем градациям доз удобрений — 0, 2, 4 и 6.

На рисунке 54, по данным таблицы 100, построена поверхность прямо-

линейной регрессии У на X и Z в трехмерном пространстве

—

плоскость ре-

грессии. На этой диаграмме урожай льна У, соответствующий определенным

комбинациям X и У, отложен по вертикальному ребру куба, осадки читаются

на правой его стороне, а дозы удобрений — на левой. Поверхность регрессии

дает четкое представление об эффекте комбинированного влияния изучаемых

факторов на результативный признак.

Необходимо подчеркнуть, что математические уравнения для парной и

множественной регрессии имеют смысл только в области фактических значе-

ний X, У и Z только тогда, когда корреляционная связь значимо отличается

от нуля.

§ 3. КРИВОЛИНЕЙНАЯ КОРРЕЛЯЦИЯ И РЕГРЕССИЯ

Если связь между изучаемыми явлениями существенно от-

клоняется от линейной, что легко установить по виду корреля-

ционной решетки или, еще лучше, по точечному графику, то ко-

эффициент корреляции непригоден в качестве меры связи. Он

может указать на отсутствие сопряженности там, где налицо

сильная криволинейная зависимость. Поэтому необходим новый

показатель, который правильно измерял бы степень криволиней-

ной зависимости. Таким показателем является корреляцион-

ное отношение, обозначаемое греческой буквой г\ (эта).

Оно измеряет степень корреляции при любой ее форме.

Корреляционное отношение при малом числе наблюдений вы-

числяют по формуле:

Ух

2(Y-y)*-Z(Y-y

(Y-У)*

где 2(У—у)

— сумма квадратов_отклоиений индивидуальных значений У от

общей средней арифметической у; 2(У—-г/*)

-— сумма квадратов отклонений

вариант от частных средних у

, соответствующих определенным, фиксирован-

ным значениям независимой переменной X.

Для вычисления корреляционного отношения значения неза-

висимого признака X располагают по ранжиру в возрастающем

порядке и разбивают весь ряд наблюдений на 4—7 групп с та-

ким расчетом, чтобы в каждой группе по ряду X было не менее

двух наблюдений. Затем определяют общую среднюю

у",

группо-

вые средние у

, соответствующие каждой фиксированной груп-

290

пе X, и суммы квадратов отклонений для общего 2

(У—у)

группового 2

(У—у

)

варьирования признака У.

При большом объеме наблюдений (/z>30) обработка мате-

риала для вычисления корреляционного отношения проводится в

корреляционной таблице. После группировки и разноски дат оп-

ределяют сумму квадратов отклонений группового варьирования

2f(y

~y)

сумму квадратов отклонений общего варьирования

2/(У—у)

и вычисляют корреляционное отношение по формуле:

« _l/"s/(y

-y)»

Сумма квадратов отклонений групповых средних у

от об-

щей средней у (групповое варьирование) характеризует ту часть

варьирования признака У, которая связана с изменчивостью

признака X. Сумма квадратов разностей между каждой датой и

общей средней у, т, е. 2f(Y-—у)

, характеризует общее варьиро-

вание признака У.

При функциональной зависимости У от X корреляционное

отношение равно единице; если оно равно нулю, то показывает

некоррелированность

от X; при промежуточном характере кор-

реляционной зависимости корреляционное отношение заключено

в пределах:

0<V<!-

Чем ближе г\

ух

к единице, тем сильнее, ближе функциональ-

ная зависимость

от X, и, наоборот, чем ближе

!1Х

к нулю, тем

слабее выражена эта зависимость.

Отношение сумм квадратов группового варьирования к об-

щему, т. е.

т\

/х

имеет самостоятельное значение. Оно показыва-

ет ту долю варьирования признака У, которая обусловлена сте-

пенью колебания признака X. Эта величина, называемая индек-

сом детерминации, определяет процент вариации У под влия-

нием X.

Ошибку и критерий существенности корреляционного отно-

шения рассчитывают по формулам:

¥~

Теоретическое значение критерия t для 5%-ного или

1%-ного

уровня значимости находят по таблице

приложений; число сте-

пеней свободы принимают равным п—2.

При обработке экспериментального материала методом дис-

персионного анализа значение

TJV

определяется как отношение

19*

291

суммы квадратов отклонений для вариантов C

к общей сумме

квадратов Су:

I VX

Су

откуда \

->/>

Су ' ~"^~~ •'»* Г Су

Критерий линейности корреляции. Для определения степени

приближения криволинейной зависимости к прямолинейной ис-

пользуется критерий F, вычисляемый по формуле:

(т)

—

)

(п—А)

F =

(1-11

)(^-2)'

где ц

— квадрат корреляционного отношения У по X; г

— квадрат коэффи-

циента линейной корреляции; л—-объем выборки; k

— число групп по ря-

ду*.

Связь можно практически принять за линейную, если ^ф<

<.F

и определять показатели для прямолинейной корреляции

и регрессии. Корреляция нелинейна, если

F<b>F

Теоретические

значения F берут из таблицы 2 приложений для

—2

и V2 —

—

п—2

степеней свободы.

Проверим линейность корреляции для г=0,74, %д;=0,80

п—

= 80 и Ь=7.

F =

(0,80

—0,74

) (80 — 7)

(1 — 0,80

)(7

•2)

Vi=5,

= 3,74;

^о

2,33

= 3,25;

=78.

Гипотеза о линейности отвергается (^>i

oi) и пользоваться

линейной корреляцией и регрессией нельзя, нелинейность значи-

ма на

1%-ном

уровне.

Криволинейные зависимости между двумя .переменными мо-

гут быть выражены в виде кривых линий регрессии и соответ-

ствующих им математических уравнений (рис. 55). Представ-

ленные на рисунке 55 кривые указывают, что криволинейная ре-

грессия—

это такая

зависимость,

когда при одинаковых прира-

щениях независимой переменной

зависимая переменная

име-

ет неодинаковые

приращения.

Эмпирические точки корреляцион-

ного поля при криволинейной корреляции располагаются около

кривых различного типа

—

пара-

бол, гипербол, логарифмических

кривых и т. п. В общем случае

все линии регрессии являются

кривыми и рассматриваемая на-

ми ранее линейная регрессия яв-

ляется простейшей зависимостью

Рис.

55. Кривые, иллюстрирующие раз-

личные типы зависимостей:

—

прямолинейная зависимость, типа Y—a+'

+ЬХ; 2 — кривая типа параболы У—а+Ь

Х+

+ЬцХ

—кривая типа lg

Y=a—ЬХ;

4—'Кри-

вая типа y=a+ib lg X,

292