Доспехов Б.А. Методика полевого опыта

Подождите немного. Документ загружается.

правильно по отношению к более устойчивым сортам. В опытах

с пропашными, овощными и плодовыми культурами, когда раз-

ная густота стояния растений является результатом действия

изучаемых вариантов, нельзя делать никаких поправок на изре-

женность.

Техника вычислений при ковариационном анализе показана

в примерах 1—2.

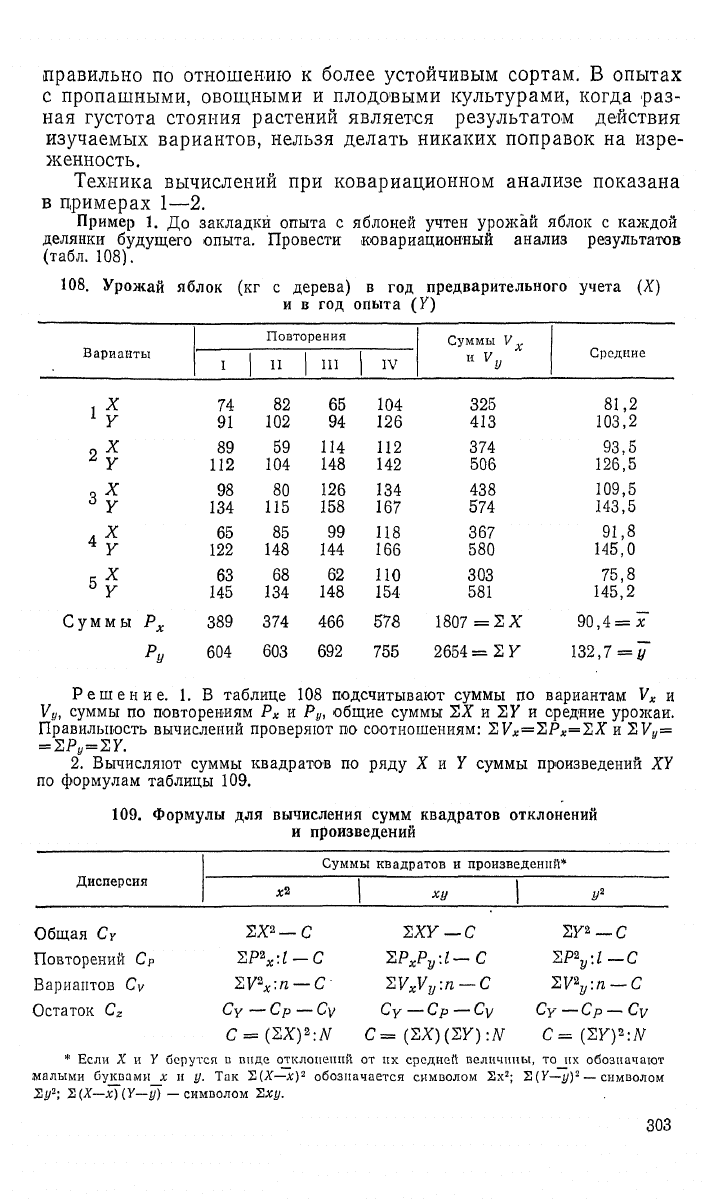
Пример 1. До закладки опыта с яблоней учтен урожай яблок с каждой

делянки будущего опыта. Провести ковариационный анализ результатов

(табл. 108).

108.

Урожай яблок (кг с дерева) в год предварительного учета (X)

и в год опыта (У)

Варианты

Повторения

III IV

Суммы V,

и V,,

Средние

1 у

4 у

О у

уммы

Рх

р„

112

134

122

145

389

604

102

104

115

148

134

374

603

114

148

126

158

144

148

466

692

104

126

112

142

134

167

118

166

ПО

154

578

755

325

413

374

506

438

574

367

580

303

581

1807= 2 X

2654 = 2 У

81,2

103,2

93,5

126,5

109,5

143,5

91,8

145,0

75,8

145,2

90,4=F

132,7=#"

Решение. 1. В таблице 108 подсчитывают суммы по вариантам V

, суммы по повторениям Р

и Р

, общие суммы

И-Х

и 2 У и средние урожаи.

Правильность вычислений проверяют по соотношениям:

='%Px='%X

и 21Л,=

=2Y.

Вычисляют суммы квадратов по ряду X и У суммы произведений XY

по формулам таблицы 109.

109.

Формулы для вычисления сумм квадратов отклонений

и произведений

Дисперсия

Общая Су

Повторений Ср

Вариантов CV

Остаток С

Суммы

Ж— с

ЪР\:1-С

ЪУ\:п —

Су

—

Ср

— Су

С = (2Х)

:# С

квадратов и произведений*

ху

HXY—C

ЪР

;1-С

:n-C

Су

— Ср — Су

= (2X)(W):N

1У*-~С

ЪР*

-Л—С

2V\:n~C

Су — Ср

—

Су

С= (2Г)

:ЛГ

* Если X и У берутся в виде отклонений от их средней величины, то_нх обозначают

малыми буквами_л; и у. Так 2(Х—я)

обозначается символом 2х

; 2(У—у)

—

символом

2(/

;

2(Х—x)(Y—у) —символом

~2>ху.

303

Суммы квадратов для ряда X:

jV = Zn=5x4=20;

С =

(2Х)

N =

(1807)

= 163 262;

Су = 2Х

—С=(74

+ 82

ПО

)—163 262=

469;

= 2PVJ

— С

= (389

+ 374

+ 466

+ 578

):5 — 163 262 = 5225;

Су==

ИУ\:п — С=

(325

+ 374

+ 438^ + 367

+ 303

) :4 — 163 262 = 2699;

= c

— С

—

Су = 10 469

—

5225

— 2699 = 2545.

Суммы произведений XY:

С= (Щ (27):W = (1807X2654):20= 239 789;

Су = 2ХУ

— С

= 246 527 — 239 789 = 6738;

= ЪР

—

С = 243 868

— 239

789 = 4079;

= ZV

Vy:

п — С

= 240 946 —

239

789 = 1157;

=Су—Ср — Су =

6738

—

4079 — 1157 = 1502.

Суммы квадратов для ряда У:

С= (2Г)

:# = (2654)

:20 =352 186;

Су = 2Г

— С= (91

+Ю2

1-154

)—

352

186= 10

354;

Ср = ЪР

*;1—С= (604

603

+ 692

755

—

352 186 = 3277 ;

Су = 2У/:п

— С

= (413

+ 506

+ 574

+ 5S0

+ 581

) :4—352JI86 = 5325;

=Cy—G

—Cy= 10 354—3277

—

5325= 1752.

Суммы квадратов записывают в таблицу ковариационного анализа

(табл. ПО) и определяют коэффициент регрессии У по X:

2ху 1502

Ьух

2х

2545

0,59 кг.

Это означает, что при изменении урожая предварительного учета X на

1 кг урожай в опыте У в среднем увеличится (или уменьшится) на 0,59 кг

с дерева.

ПО.

Результаты ковариационного анализа

Дисперсия

Суммы квадратов

и произведений

ху У*

пень

сво-

U\D

К >,

5Е*

-&0 ,

8& it

t*T&

к.

дннй

й н

Uft

ь.

Общая 10469 6738 10354 19

Повторений 5225 4079 3277 3

Вариантов 2699 1157 5325 4

Остаток I 2545 1502 1752 12

Регрессия С

— — 886,4 1

Остаток II — — 865,6 11

Сумма квадратов для регрессии

по X:

—

0,59

—

1331,2 16,91 3,36

146,0 — —

886,4 11,26 4,84

78,7 — —

(2ху)*

Сь—

>545 =886,4 при 1 степени свободы.

Остаточную сумму квадратов после корректировки опытных данных на-

ходят по разности: остаток П=остаток I—С

= 1752—886,4—865,6 при

(12—1)=Н степенях свободы.

304

Остаточная сумма квадратов для ряда У (остаток 1), которая обычно ис-

пользуется для вычисления ошибки опыта, включает два источника варьиро-

вания: собствеано случайное варьирование и варьирование, обусловленное за- *

висимостыо между урожайностью деревьев в год опыта и урожайностью их.

в год предварительного учета.

Сумму квадратов для корреляционной связи У с X (регрессию) находят

как частное от деления квадрата остаточной дисперсии ряда XY на остаточ-

ную сумму квадратов ряда X. Этой величине приписывается одна степень сво-

боды, и она вычитается из остатка 1 ряда У. В итоге получают сумму квадра-

тов для остатка II с 11 степенями свободы

(12—1

= 11). Средний квадрат вто-

рого остатка, т. е. 865,6:11=78,7, характеризует ошибку опыта после внесе-

ния поправки. Как видно из данных таблицы 110, ошибка опыта уменьшилась,

вдвое (78,7 против 146,0).

Критерий Рф находят делением среднего квадрата для вариантов и ре-

грессии на дисперсию остатка 11. Если фактическое значение регрессии боль-

ше табличного (у нас F^>F

b), то связь У с X не случайна и ее можно ис-

пользовать для корректировки опытных данных. Когда Рф-СРоб» то введение

поправок бесполезно — это не приведет к уточнению эксперимента.

В средние урожаи по вариантам вводят поправки «а регрессию, т. е.

к урожаям делянок, которые, по данным предварительного учета, оказались,

ниже среднего уровня, прибавляют величину поправки, равную byxix—X),.

а если их урожаи превышали средний уровень, то поправку вычитают

(табл. 111). Корректированные средние урожаи по вариантам приведены к ус-

ловиям полной выравненное™ предварительного учета.

111.

Внесение поправок для приведения средних урожаев в опыте (ц с 1 га)

к выравненным условиям предварительного учета

Варианты

х—Х

(x-X)=0,№-

•1х-Х)

Урожай

фактический

Корректирован-

ный У|=

У+Ь

ух

(х-Х)

81,2

93,5

109,5

91,8

75,8

я=90,4

9,2

—3,1

—19,1

—1,4

14,6

0,2

5,4

—1,8

—11,3

—0,5

8,6

0,4

103,2

126,5

143,5

145,0

145,2

7= 132,7

108,6

124,7

132,2

144,5

153,8

Yi = l

Для оценки существенности частных различий вычисляют:

*-=|/

— = |/ -4~-=4,4кг;

-l/W i/ 2x78,7

= у —^ = у £ =6,3 кг;

НСР

= ^5^=2,2x6,3= 13,9 кг.

Таким образом, все разности между средними по вариантам, превышаю»

щие 13,9 кг, существенны на 5%-ном уровне значимости.

Пример 2. В опыте с хлопчатником учтен урожай и подсчитано число рас-

тений на каждой делянке перед уборкой (табл. 112). Провести ковариацион-

ный анализ полученных данных.

Решение 1. В таблице 112 подсчитывают суммы и средние; правильность

расчетов проверяют по соотношениям: 2У

Л:

=2Р

Л:

=2Х и ЪУ

=ЪР

=?>Y.

По формулам таблицы 109 вычисляют суммы квадратов по ряду X и¥Г

и суммы произведений XY.

20—724

305

112.

Густота стояния растений X (в тыс. на 1 га) и урожаи У

(в ц с 1 га) сортов хлопчатника

Сорта

(вариант

• 1

Суммы

ы)

Ру

78,1

38,2

70,1

37,7

75,1

42,4

70,4

36,9

293,7

155,2.

Повторения

64,3

36,4

60,2

37,0

62,2

40,1

78,0

38,5

264,7

152,0

75,2

40,1

73,4

39,7

75,0

44,7

76,1

37,2

299,7

161,7

70,0

41,1

75,6

41,5

76,4

46,8

65,5

34,2

287,5

163,6

Суммы V

287,6

155,8

279,3

155,9

288,7

174,0

290,0

146,8

1145,6 = 2Х

632,5 = 2Г

Средине

71,9

39,0

69,8

39,0 •

72,2

43,5

72,5

36,7

71,6= х

39,5=#

Суммы квадратов для ряда X:

N=ln — AXi= 16;

С = (2X)

JV = (1145,6)

:16= 82025,0;

= 2Х

-С = (78,12 + 64,3*4 1-65,б

)-82025,0=497,5;

Cp=2P*

:t— С=(293,7

+ 264,7

+ 299,7

+ 287,5

):4-82025,0 = 175,5;

= 2V

— С

= (287,б

279,3

+ 288,7

+ 290,0

) :4 — 82025,0 = 17,5;

—C

— C

= 497,5 —175,5 —17,5=304,5.

Суммы произведений XY:

C=(2X)(2Y):N= 1145,6x632,5:16=45287,0;

Cy=2XY

— С

= (78,1x38,2 +64,3X36,4

65,5x34,2) -45287,0=

129,3;

= ЪР

:1-С = (293,7X155,2 -\

287,5x163,6) :4 -45287,0 = 41,3;

= 2V

:n-C= (287,6x155,8

290,0x146,8):4 -45287,0 = 2,1 j

— С

— C

= 139,3—41,3 — 2,1 =85,9.

Суммы квадратов для ряда У:

С= (2F)

:JV = (632,5)

:16= 25003,5;

CY = 2Г

= (38,2

+ 36,4

34,2

) -25003,5 = 158,0;

=2Pyj

— С

= (155,2

+ 152,0

+ 161,7

163,

)

:4 — 25003,5 = 22,2;

:П

-С

= (155,8

+ 155,9

+ 174,0

+ 146,8

):4—25003,5 = 97,7;

=Cy—C

158,0 — 22,2—97,7 = 38,1

Суммы квадратов и произведения записывают в таблицу 113 и вычис-

ляют коэффициент регрессии У по X:

85,9

ух

2хг/

"2^~

304,5 =

«•

Итак, при изменении густоты стояния растений на одну тысячу урожай

хлопчатника в среднем увеличивается (или уменьшается) на 0,28 ц с 1 га.

306

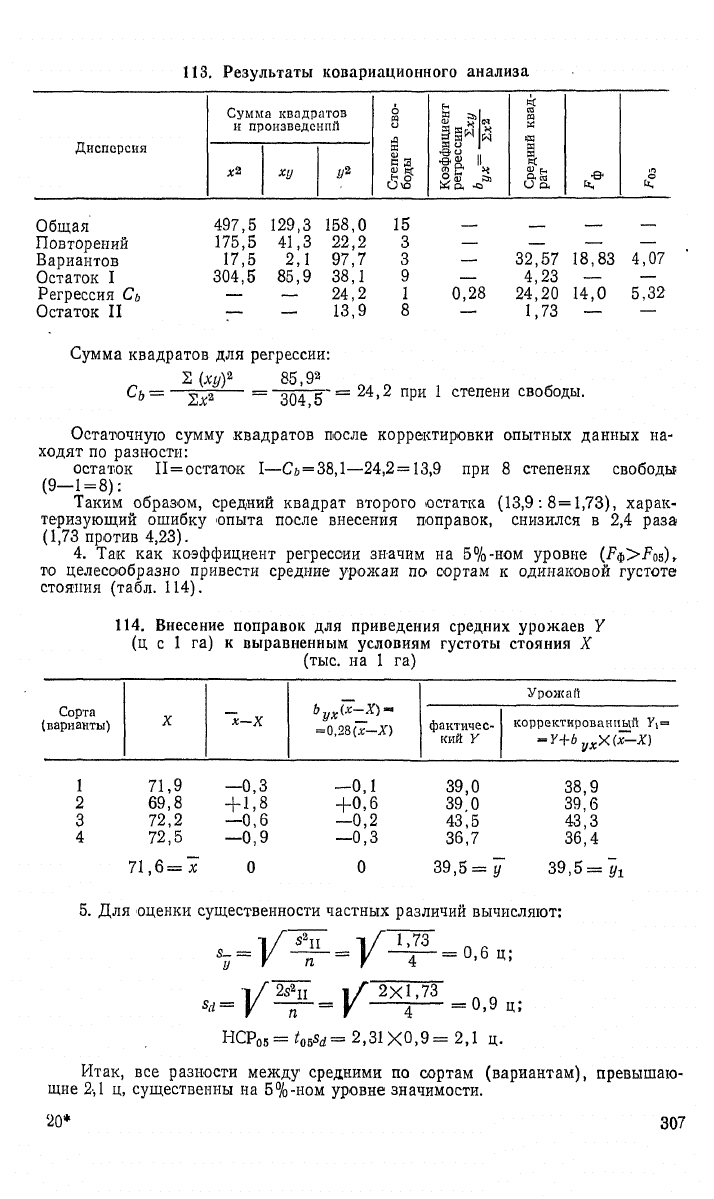
113,

Результаты ковариационного анализа

Дисперсия

Сумма квадратов

и произведений

ху

ёя

О\о

Е-

5 **

я о

во

-ей II

к а -а

вад-

&Й

О а

•&

ь.

Общая

Повторений

Вариантов

Остаток I

Регрессия Сь

Остаток II

497,5

175,5

17,5

304,5

—

129,3

41,3

2,1

85,9

—

158,0

22,2

97,7

38,1

24,2

13,9 8

— 32,57 18,83 4,07

4 23

0,28 24^20 14,0 5,32

— 1,73 — —

Сумма квадратов для регрессии:

2 {xyf 85,92

Q, = —vT2 = 3Q4 5"

степени

свободы.

Остаточную сумму квадратов после корректировки опытных данных на-

ходят по разности:

остаток П=остаток

I—С&

= 38,1—24,2=13,9 при 8 степенях свободы

(9-1 =

8):

Таким образом, средний квадрат второго остатка (13,9:8=1,73), харак-

теризующий ошибку опыта после внесения поправок, снизился в 2,4 раза

(1,73 против 4,23).

Так как коэффициент регрессии значим на 5%-ном уровне (Рф>Р

то целесообразно привести средние урожаи по сортам к одинаковой густоте

стояния (табл. 114).

114.

Внесение поправок для приведения средних урожаев У

(ц с 1 га) к выравненным условиям густоты стояния X

(тыс.

на 1 га)

Сорта

(варианты)

х-Х

ух

(х-Х)~

=0,28 (х-Х)

Урожай

фактичес-

кий Y

корректированной У\

~Y+b

X(x-X)

71,9

69,8

72,2

72,5

—0,3

_j_l

—0,6

-0,9

—0,1

+0,6

—0,2

—0,3

39,0

39 0

43,5

36,7

38,9

39,6

43,3

36,4

71,6= х

39,5= у 39,5= г/!

Для оценки существенности частных различий вычисляют:

n l/" 1,73

l/W l/ 2X1,73 .

Srf=

V Т— V 4 =0,9 ц;

HCP

=2,31X0,9=2,l Ц-

Итак, все разности между средними по сортам (вариантам), превышаю-

щие 2-,1 ц, существенны на 5%-ном уровне значимости.

307

Глава 24

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА НАСЛЕДУЕМОСТИ

Статистические методы оценки характера наследуемости се-

лектируемых признаков и комбинационной способности исход-

ных форм являются предпосылкой для рационального планиро-

вания подбора родительских пар для скрещивания и ориентиро-

вочного прогнозирования эффективности селекции. Наиболее

важное значение для этих целей имеет коэффициент наследуемо-

сти (/г

Общая фенотипическая изменчивость количественных при-

знаков (s

<j)) может быть разложена на наследственную, или ге-

нетическую

и ненаследственную (модификационную), или

паратоническую, изменчивость

обусловленную факторами

внешней среды:

Допуская, что связь генотипа с паратипом отсутствует, и при-

нимая общую фенотипическую изменчивость (s

$) за единицу,

«отношение дисперсий

<|)

и s

/s^ покажет долю (или про-

цент) генетической и пар атипической .изменчивости в общей фе-

нотипической изменчивости совокупности:

/5ф

=1 (или 100%).

Доля генетической изменчивости в общей вариабельности

признака называется коэффициентом наследуемости,

т. е.

5//

5ф

Известно несколько методов вычисления коэффициента на-

следуемости. Наибольшую известность получили способы опре-

деления /i

при помощи коэффициента корреляции пли коэффи-

циента регрессии между фенотипами родственных групп и с по-

мощью дисперсионного анализа, позволяющего разложить фено-

типическую изменчивость (s\) на составляющие ее компонен-

ты:

дисперсию генотипическую (s

) и пар атипическую

Порядок вычисления наследуемости при помощи коэффици-

ента корреляции и коэффициента регрессии показан в примере 1.

Пример 2 иллюстрирует технику расчетов h

в однофакторном,

а пример 3 —в двухфакторном дисперсионном комплексах.

Пример 1. Определить эффективность отбора растений кукурузы с высо-

ким содержанием масла в зерне (табл. 115, данные П. П. Литуяа, 1969).

Решение. 1. По исходным данным вычисляют вспомогательные вели-

чины (2,Х, 2 У, 2Z

, 2У

и 2.XY), коэффициент корреляции, регрессии и крите-

рий t

2ХУ~(2Х2У):гс

~ (2Х

—(2Х)

:я)(2Г

—(2У)

:я) ~

2762,33—

(352,22X396,41) :51

= —•— • —— 0»40:

1^(2502,52—(352,22)

:51)(3134,,14—(396,41)

:51) * '

308

115.

Содержание масла в зерне кукурузы (%)

Номер

пары

материнская

форма

(гибрид)

уз

1 6,99 9,02 48,86 81,36 63,05

2 6,99 6,94

48,86 48,16 48,51

3 7,84 8,13 61,47 66,10 03,74

51 6,57 6,42 43*17 41,22 42,16

Сумма 352,22 =2Х 396,41= 2502,52= 3134,14= 2762,33 =

= 27 = 2Х

= 2Г

= 2ЛТ

h —

2XY

~(2Xx%Y):n __ 2762,33 —(352,22x396,41 ):51 _

nofi

YX—

—(2Х)

:я 2502,52 —(352,22)2:51 ' '

/ -

- °'

o,m-

/1—2

51—

49;

= 2,00.

По /-критерию (/ф>^об) корреляция и регрессия значимы на

5%-ном уровне, нулевая гипотеза о независимости Y от X от-

вергается и, следовательно, на основе г и Ъ

ху

можно вычислить

коэффициент наследуемости /г

Коэффициент наследуемости вычисляют, исходя из теоре-

тических допущений о' том, что /г

равен удвоенному коэффици-

енту корреляции или регрессии между фенотипами родителей и

потомством:

№ = 2г = 2x0,40 = 0,80 (или 80 %) ;

/г

= 2b,

= 2x0,35 =0,70 (или 70 %).

Считается, что /г

, вычисленный по коэффициенту регрессии

по X, является более точной величиной. Таким образом, пример-

но 70% фенотипической изменчивости в содержании масла обу-

словлено наследственной изменчивостью растений кукурузы, и

отбор зерна по этому признаку должен быть эффективен.

Пример 2. По данным учета массы зерна с одного колоса гибридов пше-

ницы (табл. 116) вычислить коэффициент наследуемости методом дисперсион-

ного анализа.

Решение. 1. Проводят дисперсионный анализ для однофакториого ком-

плекса:

N= In = 4x5 =20;

C = (2X)

:W = 74,7

:20 = 279,00;

=2X

-C= (5,5»+ 4,14

1~4>4

)

—279,00= 22,91 ;

>=2P2

J-C=

(21,l

+ 15,9

+...+16,l

):4-279,00=20,25;

.= 2^:n-C=(18,6

4-17,2

+18,02 + 20,9

):5-279,00= 1,52;

= C

— С

—

= 22,91 — 20,25 — 1,51 = 1,14.

309

116.

Масса зерна с одного колоса гибридов (г)

Название гибрида

материнская

форма

отцовская

форма

1 1

1 2

1 3

1 4

Сумм

Ы Р

5,5

5,0

5,2

5,4

21,1

Повторения,

4,1

3,1

3,7

5,0

15,9

3,0

3,2

3,4

12,6

2,2

2,1

2,0

2,7

9,0

3,8

4,0

3,9

4,4

16,1

Суммы

18,6

17,2

18,0

20,9

74,7

Средний

3,72

3,44

3,60

4,18

= 2Х

Полученные результаты записывают в таблицу дисперсионного анализа

и определяют значимость действия генотипов на фенотипическую изменчивость

признака по /-"-критерию (табл. 117).

117.

Результаты дисперсионного анализа

Дисперсия

Сумма

квадратов

Степени

свободы

Средний

квадрат

^05

Общая

Повторений

Отцовских форм

Остаток (ошибки)

22,91

20,25

1,52

1,14

—

0,5066

0,0950

5,33

3,49

Влияние отцовской формы на среднюю массу зерна с одного колоса ока-

залось существенным

{F$>FU?,),

имеет смысл вычислить коэффициент насле-

дуемости, характеризующий степень генетической изменчивости.

Необходимо указать, что дисперсия групповых средних имеет сложную

природу. Она определяется как генотишяеской изменчивостью признака $Д

так и случайной, пар атипической изменчивостью s

. Таким образом, средний

квадрат для вариантов в нашем примере отцовских форм s

состоит из двух

компонентов: Sv

+ns

. Здесь п поставлено перед генотипическрй изменчи-

востью групповых средних для того, чтобы привести ее к уровню первичных

наблюдений. Используя приведенное выше соотношение, по данным дисперси-

онного анализа легко определить генотипическую и общую фенотипическую из-

менчивость:

S]/

Вычисление генотипической и фенотипической изменчивости и коэффи-

циента наследуемости по результатам дисперсионного анализа:

*—s*

0,5066

—

0,0950

„

= 5

=0,0823;

s^^s^

+ s*^ 0,0823 + 0,0950= 0,1773;

0,0823

"^Ф

'0Л773

(

или4б

%)-

Таким образом, коэффициент наследуемости, характеризующий степень

передачи селектируемого признака

—

масса зерна с одного колоса

—

от отцов-

ской формы к гибриду, равен 0,46 и, следовательно, браковка и отбор по этому

признаку должны быть эффективны.

Пример 3. По данным учета числа зерен в колосе у гибридов ячменя

(табл. 118) вычислить коэффициент наследуемости методом дисперсионного

анализа.

310

118.

Число зерен в колосе у гибридов ячменя

Материн-

ская

форма

Отцовская

форма

Повторения

Суммы

Средние

Суммы

Решение

плекса:

Ьг

Пр1

143

145

146

83 20,8

76 19,0

88 22,0

93 23,2

112 28,0

123 30,8

575 = 2Х

Проводят дисперсионный анализ для двухфакторного ком-

N = Ыв

= 3X2X4 =24

;

С= (2X)

:W=575

:24 = 13776,04;

Су = 2Х

— С= (20

+ 202-1

) —13776,04= 428,96;

Ср=ЯР*:1

— С= (141

+ 143

+ 145

+ 146

):Зх2 —13776,04= 2,46;

Су = 2V

:n — С= (83

+ 76

\-123

) :4— 13776,04 =

406,71;

=:C

—C

= 428,96—2,46—406,71 = 19,79.

Для оценки существенности действия материнских и отцовских форм и

их взаимодействия на результативный признак гибридов составляют табли-

цу 119, в которую вписывают суммы V для каждого гибрида и находят сум-

мы по факторам А я В.

119.

Таблица сумм для определения эффектов А, В

и взаимодействия АВ

Фактор

fli

йг

Суммы В

112

283

Фактор

Ъг

123

292

Суммы

159

181

235

575 = 2Х

Дисперсионный анализ данных таблицы 119 дает:

общее варьирование

СА+В+АВ—

внутренняя часть таблицы (численно

+B+AB=C

=AQQ,7\

И вычислено нами ранее), варьирование факторов А к В.

Взаимодействие АВ находят по разности:

= ИА

п—С= (159

+181

+235

) : 2X4—13 776,04=382,34 при {U—1) = (3—1)=2 степенях свободы;

=25

:/лл—С=(283

+292

) : 3X4—13 776,04=3,38 при

—

1) - (2—

= 1

степени свободы;

САЪ=С

+В+АВ—СА—С

**Ш,71—

382,34—3,38=20,99 при

iU—l)

(/в—1)

= (3—1) (2—1) =2 степенях свободы.

Составляют таблицу дисперсионного анализа и оценивают существен-

ность действия и взаимодействия по критерию F (табл. 120).

В рассматриваемом примере существенном оказалось действие А (мате-

ринских форм) и взаимодействие АВ (материнская формах отцовская фор-

ма).

Следовательно, имеет смысл вычислить коэффициенты наследуемости, ха-

рактеризующие силу генетического влияния материнских форм и взаимодей-

ствия; вариабельность числа зерен в колосе у гибридов ячменя не зависит су-

щественно от отцовских форм (Рф</

05)-

311

120,

Таблица дисперсионного анализа

Дисперсия

Сумма

квадратов

Степени

свободы

Средний

квадрат

^05

428,96.

2,46

382,34

3,38

20,99

19,79

—

191,17

3,38

10,50

1,32

—

144,83

2,56

7,95

—

3,60

4,54

3,60

—

Общая

Повторений

Материнских форм

Отцовских форм

Взаимодействия

АВ

Остаток

двухфакторыом комплексе дисперсия групповых средних имеет более

сложную природу,

чем в

однофакторном,

определяется

как

генетической

из*

менчивостыо, обусловленной генотипами материнских

отцовских форм

и их

взаимодействия,

так и

случайной, паратипической, изменчивостью (остаток).

Общий коэффициент наследуемости

этом случае равен:

Для уяснения сущности вычислительных операций

при

определении дис-

персий, характеризующих влияние

на

фенотипическую изменчивость генотипов

материнских форм

отцовских форм

) и их

взаимодействия (з

да)*

целесообразно рассмотреть схему компонентного анализа двухфакторного экс-

перимента (табл. 121).

121.

Компонентный анализ двухфакторного комплекса

Дисперсия

Оцениваемые параметры

Материнских форм

Отцовских форм

Взаимодействия

АВ

Ошибка

Исходя

из

этой схемы дисперсии

S*AB

можно вычислить

по

фор-

мулам:

P +

n&AB

lB&Ai-P

'&AB)

В нашем примере существенным оказалось влияние материнских форм

и взаимодействия

АВ.

Поэтому имеет смысл вычислить только

две

дисперсии

AB)

два коэффициента наследуемости (Л

л и

АВ)

312