Доронин С.В., Бабушкин А.В. Механика разрушения. Разрушения и дефектность технических систем

Подождите немного. Документ загружается.

Технология моделирования с использованием суперэлементов состоит

в следующем. Предварительно выполняют так называемую процедуру кон-

денсации, позволяющую объединить произвольное число обычных конечных

элементов в суперэлемент с эквивалентными жесткостными характеристика-

ми. Далее приведенный суперэлемент включают в конечно-элементную мо-

дель на правах обычного конечного элемента.

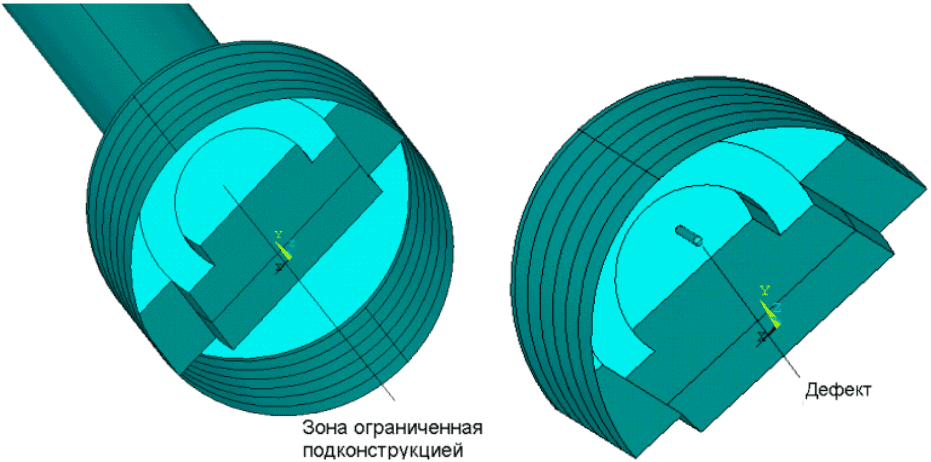
Рассмотрим пример результатов моделирования НДС в области техно-

логической дефектности крупногабаритных вал-шестерен. Разработана объ-

емная твердотельная модель детали с подконструкцией, содержащей дефект

в виде полости заданных формы, размеров, местоположения (рис. 26).

Рис. 26. Фрагмент модели вала-шестерни с подконструкцией

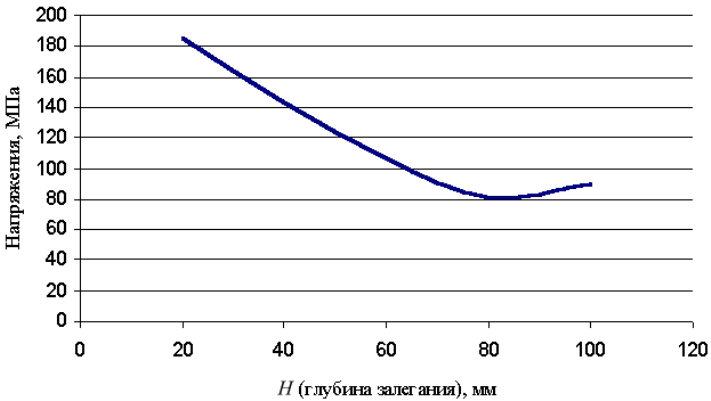
Выполнена серия расчетов с целью исследования зависимости макси-

мальных напряжений в области дефекта от глубины его залегания (рис. 27),

диаметр и длина приняты постоянными.

Аналогичные зависимости построены для переменных значений длины

и диаметра дефекта, что позволяет выявить наиболее неблагоприятные ком-

бинации линейных размеров дефекта, приводящие к максимальным значени-

ям напряжений.

3.2. Конечно-элементное моделирование НДС

в области эксплуатационных трещин

Особенности моделирования НДС в области трещин в реальных эле-

ментах конструкций вытекают из следующих соображений. Во-первых, тре-

щина является наиболее острым концентратором, поэтому в области у ее

вершины наблюдают весьма высокие абсолютные значения и градиенты на-

пряжений. Во-вторых, вследствие значительной концентрации даже при не-

больших номинальных напряжениях абсолютные уровни напряжений в вер-

шине трещины таковы, что в большинстве случаев необходимо решение не-

линейной упруго-пластической задачи. В-третьих, в механике разрушения

обычно рассматривают прямолинейный математический разрез как теорети-

ческую модель трещины. При этом принимают нулевое расстояние между

берегами трещины. Сложности, возникающие при попытках моделирования

указанного нулевого расстояния, обходят путем отбрасывания части конст-

рукции и учета условий симметрии наложением соответствующих гранич-

ных условий (рис. 28). В реальных же элементах конструкций траектории

трещин имеют более сложную конфигурацию, условия симметрии практиче-

ски никогда не удается обоснованно использовать.

Рис. 27. Зависимость максимальных напряжений в области дефекта от глу-

бины его залегания

Указанные особенности при моделировании эксплуатационных трещин

учитывают следующим образом.

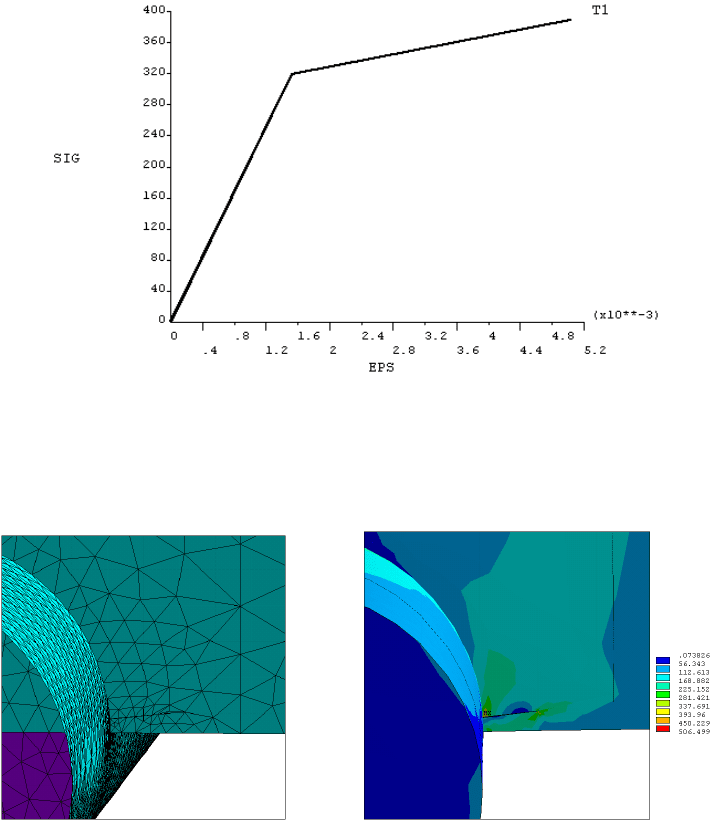
Во-первых, в области трещины выполняют многократное измельчение

сетки с последовательным уменьшением конечных элементов в области ост-

рой вершины (рис. 29).

Во-вторых, используют одну из известных моделей упрочнения мате-

риала. При этом определяют форму и количественные параметры диаграммы

деформирования (рис. 30). Анализ НДС представляет собой нелинейную

процедуру, в ходе выполнения которой осуществляется постепенное прира-

щение нагрузки. По мере достижения в отдельных конечных элементах пре-

дела текучести в них переопределяют свойства материала с учетом упрочне-

ния. Эту последовательность вычислений повторяют до достижения номи-

нального уровня внешних нагрузок.

Рис. 28. Моделирование условий симметрии в плоскости трещины

а б

Рис. 29. Измельчение сетки в области вершины трещины: а – полная модель;

б – область вершины трещины

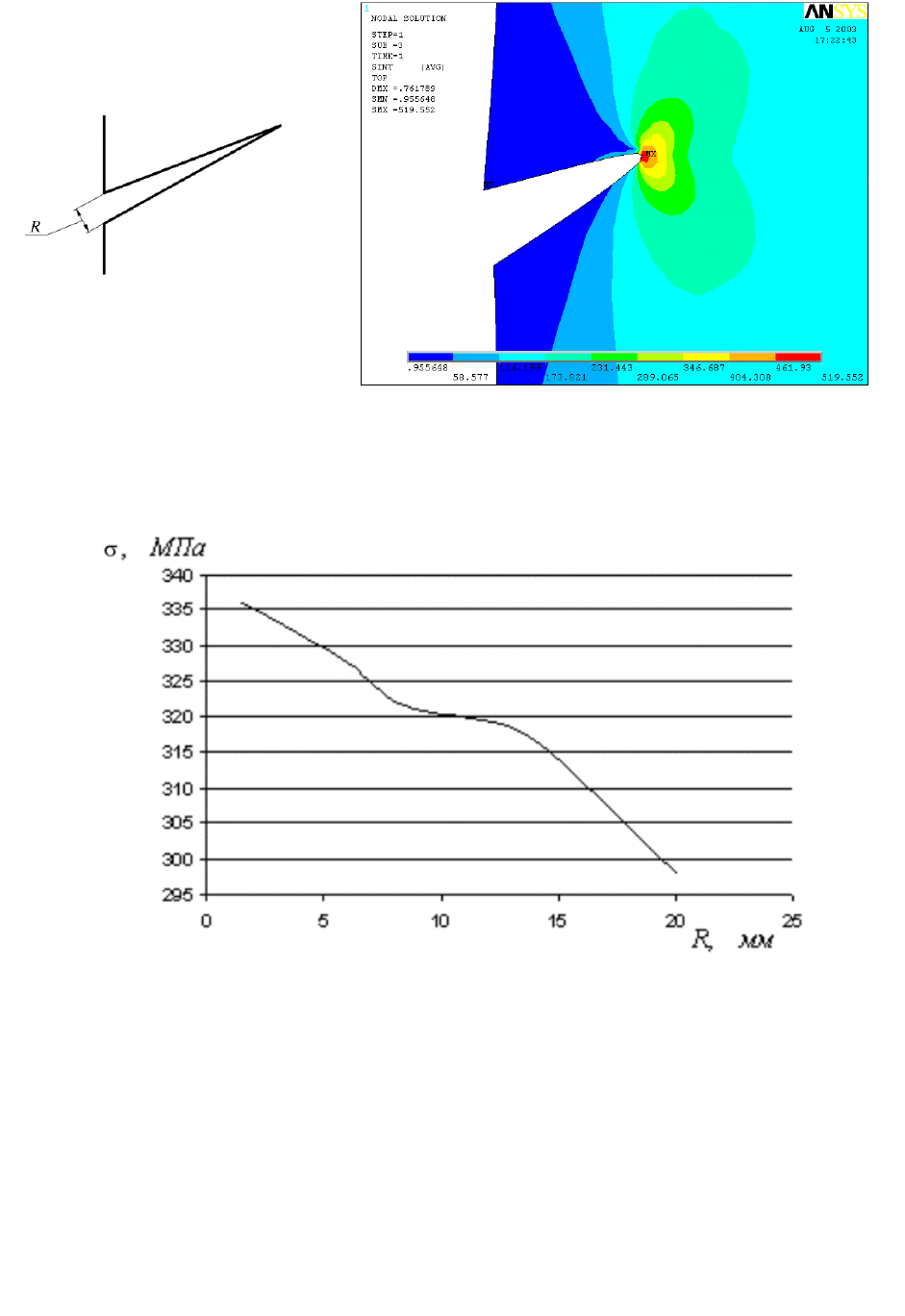
В-третьих, моделируют реальную конфигурацию траектории трещины

(рис. 31). В этом случае получают результат, не поддающийся какому-либо

обобщению, но приемлемый для решения задач индивидуального прогнози-

рования ресурса, вероятности разрушения, показателей риска. Для получения

более общих результатов используют упрощенные схематизации особенно-

стей траектории трещины, выдерживая лишь основное ее направление

(рис. 32). При этом выполняется несколько расчетов с изменением расстоя-

ния между берегами трещины. По результатам этой серии расчетов выполня-

ется экстраполяция компонент напряжений и деформаций при стремящемся к

нулю расстоянии между берегами трещины (рис. 33).

Рис. 30. Модель упругопластического поведения материала

а б

Рис. 31. Моделирование трещины произвольной конфигурации: а – конечно-

элементная сетка; б – распределение интенсивности напряжений

Рис. 32. Интенсивность напряжений в области вершины краевой трещины

длиной 100 мм, расположенной под углом 25

в прямоугольной пластине

Рис. 33. Экстраполяция интенсивности напряжений в вершине трещины при

стремлении к нулю расстояния между ее берегами

3.3. Гранично-элементное моделирование НДС

в области трещиноподобных дефектов

Метод граничных элементов (МГЭ) имеет ряд преимуществ перед ме-

тодом конечных элементов. МГЭ уменьшает размерность исходной задачи на

единицу, т. е. для двумерных задач получается одномерное граничное инте-

гральное уравнение, а для трехмерных задач – всего лишь двумерные инте-

гральные уравнения по поверхности. Можно заключить, что сопоставляе-

мые времена решения трехмерных задач методом конечных элементов и

методом граничных элементов при близкой точности обычно оказываются

в 4–10 раз меньше для последнего метода [49]. Эта разница могла бы

быть гораздо больше для определенных классов задач, которые особенно

благоприятны для МГЭ, например для следующих. 1. Системы, границы

которых частично находятся в бесконечности. Поскольку процедура ре-

шения МГЭ автоматически удовлетворяет допустимым граничным услови-

ям на бесконечности, разбиение этих границ не требуется, в то время как

в методе конечных элементов границы в бесконечности должны быть

аппроксимированы значительным количеством удаленных элементов. 2.

Системы, содержащие полубесконечные области с «ненагруженными»

участками свободной границы. И в этом случае вообще нет необходимо-

сти дискретизировать «ненагруженные области», обычно составляющие

большую часть свободной поверхности, если использовать возможность

выбора в МГЭ подходящего сингулярного решения.

Применительно к задачам моделирования НДС в области трещин и

других острых концентраторов МГЭ получил меньшее распространение

по сравнению с МКЭ. С теоретической точки зрения эти задачи характе-

ризуются разрывами в геометрии и классифицируются как задачи о реб-

рах и углах [49]. Наиболее простой подход к рассмотрению этих задач

может состоять в том, чтобы закруглить ребра и углы. Получающиеся

при этом результаты будут точными вдали от областей закругления и

не столь точными вблизи них. Этот подход был реализован в первом по-

колении вычислительных программ с использованием непрямой форму-

лировки МГЭ. Однако эти решения неприемлемы в задачах о трещинах,

так как важнее всего знать решение на разрыве или вблизи него. В связи

с этим был разработан ряд процедур для моделирования таких разрывов

с использованием как прямого, так и непрямого методов (использование

одного узла, концепция независимых кратных узлов, концепция кратных

узлов с дополнительными соотношениями, использование специального

набора ядер, заранее удовлетворяющих дифференциальным уравнениям

и определенным граничным условиям в угловой точке) [49]. В дальней-

шем были разработаны специальные технологии МГЭ, направленные

именно на моделирование задач о трещинах.

Одной из таких технологий является совместное применение сле-

дующих двух усовершенствований [50]. Во-первых, непрерывный контур

границы заменяется сегментами дуг окружностей, а не прямолинейными

сегментами. При этом каждый дуговой сегмент ограничен двумя узлами

(концевыми точками) и разделен пополам еще одним узлом (средней

точкой). Таким образом, в разбиении границы участвуют в два раза

больше узлов. Во-вторых, моделирование на каждом сегменте вектора

граничных напряжений и перемещений осуществляется при помощи от-

резков парабол, а не линейных функций или постоянных. Такие аппрок-

симации определяются на каждом сегменте по трем узловым значениям.

Все функции должны быть непрерывны в средних точках, однако допус-

каются разрывы вектора напряжений в концевых точках, которые можно

располагать в углах.

Еще одним направлением математического моделирования трещин

с использованием МГЭ является использование специальной функции

Грина [51]. Однако в этом случае рассматриваются только объекты, со-

держащие единственную прямолинейную трещину, причем обязательным

условием оказывается наличие симметрии, и плоскость трещины выбира-

ется в качестве плоскости симметрии.

Получили распространение технологии гранично-элементного мо-

делирования, известные как методы фиктивных нагрузок и разрывных

смещений [52].

Метод фиктивных нагрузок предполагает деление границы рас-

сматриваемой области на ряд элементов и сопоставление каждому эле-

менту фиктивных нагрузок. Далее составляют и решают систему алгеб-

раических уравнений, чтобы найти такие фиктивные нагрузки, которые

обеспечивают заданные на границе смещения или напряжения. Наиболее

обоснованно метод применяют для решения задач о полости в бесконеч-

ных телах и не дает необходимой точности при решении задач о трещи-

нах.

Метод разрывных смещений основан на аналитическом решении

задачи о бесконечной плоскости, смещения в которой терпят постоянный

по величине разрыв в пределах конечного отрезка. Физически разрыв

смещений можно представить как линейную трещину, противоположные

поверхности которой смещены относительно друг друга. Метод разрыв-

ных смещений основан на представлении, что непрерывно распределен-

ные вдоль трещины разрывы смещений можно заменить дискретной ап-

проксимацией.

Методы фиктивных нагрузок и разрывных смещений могут быть при-

менены при решении задач о влиянии дефектов сплошности (технологиче-

ских дефектов и эксплуатационных трещин) на конструкционную прочность.

Рассмотрим алгоритмы и вычислительные реализации таких задач. В основу

разработанного программного обеспечения положены написанные на языке

FORTRAN модули TWOFS и TWODD [52], переведенные на язык С++ и

снабженные рядом дополнительных возможностей. Основные усовершенст-

вования связаны с развитием интерфейса пользователя (как удобные окна

ввода исходных данных, так и новые возможности визуализации результа-

тов), расчетом некоторых параметров механики разрушения, а также с вклю-

чением модулей гранично-элементного моделирования в схему алгоритма

метода статистических испытаний (Монте-Карло).

Алгоритм и программа собственно гранично-элементного моделирова-

ния имеют очень простую структуру и сводятся к выполнению следующих

шагов:

1. Определение местоположений всех граничных элементов и задание

для каждого из них граничных условий в смещениях или напряжениях.

2. Вычисление граничных коэффициентов влияния и построение соот-

ветствующей системы линейных уравнений с учетом граничных условий на

каждом элементе.

3. Решение системы уравнений, построенной на втором шаге.

4. Вычисление смещений и напряжений на каждом граничном элемен-

те.

5. Вычисление коэффициентов влияния для заданных внутри рассмат-

риваемой области точек и, следовательно, вычисление смещений и напряже-

ний в этих точках.

Рассмотрим особенности практического применения разработанных

алгоритмов и программного обеспечения.

На первом этапе выполняют определение вида дефекта (эллиптическая

или острая трещина), задают его размеры и приложенные номинальные на-

пряжения по одной или двум осям (рис. 34).

Далее выполняют непосредственно алгоритм, реализующий метод

фиктивных усилий или разрывных смещений. Для визуализации расчета на-

пряженного состояния в области дефекта разработан следующий подход. Из

исходной расчетной точки (например вершины трещины) в пространстве, ог-

раниченном осями X и Y, проводится с заданным угловым шагом ряд лучей,

вдоль которых с некоторым линейным шагом определяется положение сис-

темы расчетных точек, в которых вычисляются и выводятся компоненты на-

пряжений и деформаций. Общая картина напряженного состояния дается од-

новременной визуализацией двух главных напряжений, причем первое глав-

ное определяется цветом, а второе – диаметром расчетной точки (рис.

35). Здесь же выводится оценка коэффициента интенсивности напряжений в

исходной расчетной точке. Результаты расчетов выводятся также в текстовом

формате в отдельный файл и могут быть использованы для дальнейшей об-

работки.

Рис. 34. Определение исходных данных

Рассмотрим в качестве примеров результатов следующие расчетные

зависимости.

Для эллиптического сквозного дефекта с большой а и малой с полу-

осями, находящегося в поле растягивающих напряжений 100 МПа, исследо-

вано влияние остроты дефекта на максимальные значения нормальных ком-

понент напряжений для плоского напряженного состояния. Для этого выпол-

нена серия расчетов, в ходе которых длина малой полуоси была фиксирована

(с = 5), а длина большой варьировалась в достаточно широких пределах. Рас-

тягивающие напряжения прикладывались нормально большой полуоси. По

мере увеличения длины большой полуоси форма эллиптического дефекта

приближалась к острой трещине, одно из нормальных напряжений нелиней-

но возрастало, а второе стабилизировалось на уровне порядка 300 МПа, соот-

ветствующем теоретическому коэффициенту концентрации 3 у круглого от-

верстия (рис. 36).

Аналогичные серии расчетов выполнены при других соотношениях

длин полуосей эллиптического дефекта, а также для острой трещины в плос-

ком элементе конструкции. Полученные результаты свидетельствуют об аде-

кватности использованных алгоритмов и разработанного программного

обеспечения.

Рис. 35. Визуализация плоского напряженного состояния

100

200

300

400

50 40 30 20 10 5

Напряжения, МПа

Напр. по Y Напр. по Х

Рис. 36. Зависимость нормальных напряжений от остроты

эллиптического дефекта