Доронин С.В., Бабушкин А.В. Механика разрушения. Разрушения и дефектность технических систем

Подождите немного. Документ загружается.

cos

sin

cos

cos2

sin































sin

sin1

cos





























,0,





















yzxzyxz

cos22

sin

























;0,

sin21

cos



























продольный сдвиг (тип III)

cos

sin















yzxz

sin

























xyzyx

где K

, K

III

– коэффициенты интенсивности напряжений для трещин соот-

ветствующего типа.

Эти формулы были получены для случая плоской деформации; в слу-

чае плоского напряженного состояния нужно взять в них 

=0 и заменить 

на /(1+). Формулы справедливы в малой окрестности края трещины, т. е. r

должно быть малым по сравнению с характерным линейным размером тела,

например длиной трещины или расстоянием ее конца от свободной границы.

Трем типам разрывов в теории дислокаций соответствуют клиновые,

краевые и винтовые дислокации. Для трещин произвольного типа все вели-

чины K

, K

III

отличны от нуля. Эти величины называются коэффициента-

ми интенсивности напряжений и имеют размерность силы, деленной на дли-

ну в степени три вторых.

Рассмотренные классические модели описывают характер распределе-

ния напряжений вокруг линейной бесконечно острой трещины (математиче-

ского разреза). Кроме того, решены следующие смежные математические за-

дачи теории упругости [28]: для пространства с шаровой полостью, кругово-

го конуса и клина, цилиндра с внешним кольцевым разрезом, плоских тел с

разрезами и ряд других. Большое количество расчетных схем для плоских

трещиноподобных дефектов (вырезы различной формы и ориентации) и го-

раздо меньшее для объемных дефектов представлено в [29].

Более сложными оказываются модели трещин в упругопластической

постановке [32]. Здесь необходимо отметить следующие основные подходы:

1) решение Ирвина о размере пластической зоны в вершине трещины пред-

полагает рассмотрение эквивалентной трещины, длина которой увеличена на

размер пластической зоны; 2) модели с силами сцепления у вершины трещи-

ны для учета пластической релаксации напряжений (Баренблатт, 1959 г., [33];

Дагдейл, 1960 г., [34]; Витвицкий, Леонов 1960 г., [35]; Билби, Коттрелл, Су-

инден 1963 г., [36]).

Известен ряд исследований, развивающих вероятностные подходы

к моделям дефектности. Здесь существует два различных подхода. Во-

первых, рассматривается одиночный дефект, параметры которого являются

случайными величинами и описываются вероятностными распределениями

[30]. Во-вторых, прочность и разрушения рассматриваются в связи со слу-

чайным рассеянием системы трещин в твердом теле [31].

Более широкая постановка исследований процесса разрушения привела

к тому, что было введено более общее понятие повреждения материала кон-

струкции. Под этим в зависимости от конкретных условий можно понимать

как трещину произвольных форм и размеров, так и систему трещин, а, кроме

того, рассеянные повреждения материала и другие дефекты. Основой для

выработки общего подхода к повреждениям различной физической природы

является то, что для их описания используют одни и те же или очень близкие

математические соотношения. Кроме того, много общего есть также в техни-

ке применения полуэмпирических моделей для расчета и прогнозирования

ресурса [37]. Самые простые модели основаны на введении скалярной меры

повреждений, представленной функцией времени. Нулевое значение функ-

ции соответствует отсутствию повреждений, единичное – уровню поврежде-

ний, при котором объект выработал свой ресурс. Выбор физических состоя-

ний, отвечающих крайним значениям функции, достаточно произволен. Од-

ной из наиболее распространенных моделей является корректированная ли-

нейная гипотеза суммирования усталостных повреждений, позволяющая

учесть нерегулярный характер нагруженности [38].

Вероятностные модели накопления повреждений [39] в виде вложен-

ных цепей Маркова являются моделями более широкого класса и позволяют

учитывать произвольную природу повреждений конструкционного материа-

ла: коррозия, эрозия, износ, ползучесть, выносливость, рост усталостных

трещин, старение полимеров и т. п.

Рассмотрение пластических явлений в вершине трещины, условий об-

разования и роста пор, а также поведения дислокаций [40] позволило сфор-

мулировать меру повреждаемости, основанную на соотношении размеров

растущих пор.

Эти и другие меры поврежденности являются феноменологическими

моделями и в большинстве случаев мало связаны с реальными дефектами

конструкционных материалов.

Итак, рассмотренные модели дефектности фактически представляют

собой ряд расчетных схем и выведенных для них математических выражений

для оценки параметров НДС и механики разрушения. В реальной же инже-

нерной практике приходится иметь дело с дефектами, в большинстве случаев

мало соответствующих ограниченному набору расчетных схем. При этом

фактически единственным инструментом исследования поведения повреж-

денного материала оказывается численное моделирование реальных пара-

метров дефектности с использованием методов конечных разностей, конеч-

ных и граничных элементов.

2.2. Методы схематизации и моделирования дефектности

Механика разрушения представляет собой раздел механики деформи-

руемого твердого тела, рассматривающий вопросы прочности конструкций с

начальными повреждениями. При этом одним из наиболее важных этапов

применения механики разрушения является принятие гипотезы о том, с ка-

ким дефектом приходится иметь дело в данном конкретном случае, так как

это определяет применяемые модели напряженного состояния, разрушения,

и, в конечном счете, позволяет дать ответ на вопросы об опасности дефекта и

живучести конструкции. Существует два принципиально разных подхода к

моделированию дефектности: физико-математический (сведение произволь-

ных дефектов и их систем к ограниченному набору расчетных схем) и фено-

менологический (использование абстрактной меры поврежденности, слабо

связанной с физическими процессами в конструкционном материале). Фено-

менологический подход развивается вне рамок механики разрушения и явля-

ется предметом теории надежности механических систем [41]. Рассмотрим

известные методы моделирования дефектности, позволяющие перейти от

произвольной дефектности к моделям дефектности, используемым в механи-

ке разрушения. Такая процедура называется схематизацией дефектности.

Схематизация дефектности затруднена, в частности невозможностью

однозначной интерпретации результатов неразрушающего контроля. В зави-

симости от ориентации дефекта относительно дефектоскопа могут быть по-

лучены существенно различные значения его площади. В связи с этим, на

первом этапе целесообразно таким образом интерпретировать результаты

дефектоскопического контроля, чтобы получить максимальную площадь де-

фекта, обеспечив все последующие результаты в запас прочности [42]. Де-

фекты характеризуются многообразием форм, размеров, местоположения.

При схематизации технологическую дефектность приводят к эквивалентной

трещине [43–45], при этом любые дефекты рассматривают как трещины, по-

скольку они являются наиболее опасными. Схематизации подвергают гео-

метрические параметры элемента конструкции и дефекта. Методические ре-

комендации [45] регламентируют местоположение дефектов, их ориентацию

в пространстве и расстояние между ними для отнесения к тому или иному

типу. Для схематизации подповерхностного дефекта необходимы как мини-

мум наименьшая площадь проекции дефекта и глубина его расположения.

Схематизация поверхностного дефекта в качестве исходной требует инфор-

мацию о максимальной площади проекции дефекта. По известным данным

неразрушающего контроля определяют размеры полуэллиптической трещи-

ны. Если ориентация дефекта не задана, трещина располагается так, что мак-

симально ослабляет сечение элемента конструкции. При составлении расчет-

ных схем руководствуются принципом: любая дополнительная информация о

схематизируемом дефекте должна снижать консервативность расчетной схе-

мы [43].

Не вдаваясь в природу дефектов сварки и рассматривая те из них, кото-

рые существенно ослабляют металл шва, рекомендовано все технологические

дефекты сварки дифференцировать на компактные – сферические или диско-

вые и протяженные – объемные или плоские [46]. Для последних характерно,

что один из размеров значительно превосходит два других. Это позволяет

при анализе концентрации напряжений и деформаций в районе таких дефек-

тов ограничиваться решением плоской задачи теории упругости или пла-

стичности. Для сферических или дисковых дефектов аналогичный анализ

может быть выполнен при решении объемной или осесимметричной задачи.

Концентрация напряжений и деформаций в районе дефекта определяется в

первую очередь его конфигурацией (в основном радиусом кривизны в вер-

шине дефекта) и достигает максимальных значений на продолжении малой

полуоси дефекта, ориентированной перпендикулярно к действующим напря-

жениям. За характеристический размер дефекта, расположенного в поле рав-

номерных напряжений растяжения, принимают тот размер, который опреде-

ляет область возникновения и максимальные напряжения при рассмотрении

изменения напряженного состояния вдоль контура дефекта.

Для схематизации дефектности в задачах механики разрушения пред-

лагается использовать идеализированные модели дефектов [47]. В частности,

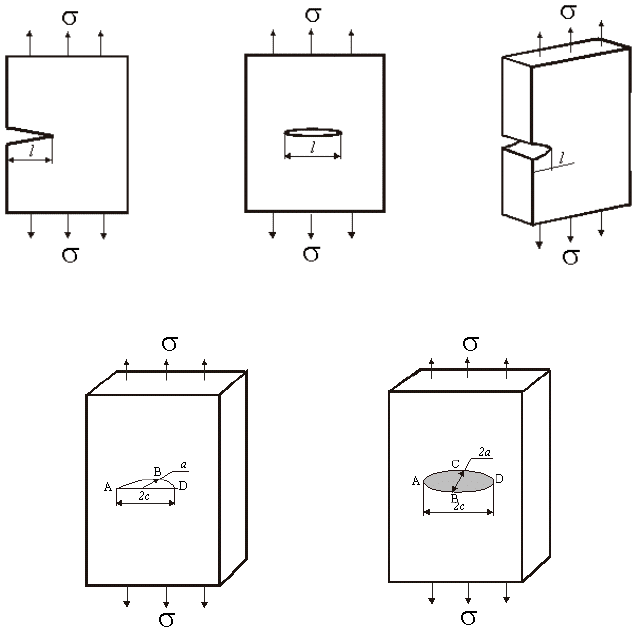
все многообразие трещин представляется четырьмя моделями: сквозной,

краевой, поверхностной полуэллиптической и внутренней полуэллиптиче-

ской трещинами нормального отрыва (рис. 16). Принимая во внимание со-

стояние современных методов проектирования, норм допустимой дефектно-

сти, методов технической диагностики и средств неразрушающего контроля,

можно полагать, что основной практический интерес для риск-анализа [47]

представляют полуэллиптические и эллиптические трещины, размеры кото-

рых сопоставимы с характерными размерами элементов конструкций. Про-

тяженные сквозные и краевые трещины можно рассматривать в теоретиче-

ском аспекте, поскольку они крайне редко допускаются в несущих конструк-

циях. Реально они могут возникать только в процессе длительной эксплуата-

ции, при этом в процессе обязательной периодической технической диагно-

стики эти дефекты неизбежно выявляются и устраняются.

Более сложной оказывается задача при наличии технологических де-

фектов, формы которых существенно отличаются от трещин. Здесь имеет ме-

сто еще большее разнообразие размеров и форм. Используя тот же подход

идеализации геометрии, все дефекты подобного типа предлагается рассмат-

ривать как сферические или эллипсоидальные включения и газовые полости

в пространстве (рис. 17).

Все рассмотренные методы и модели схематизации реализуют детер-

минированный подход, дающий консервативные оценки параметров дефект-

ности. Вместе с тем, учитывая, что неопределенность является характерной

чертой основных параметров дефектности, более перспективными являются

вероятностные подходы.

а б в

г д

Рис. 16. Типовые расчетные модели элементов конструкций с трещинами

Учитывая статистический характер дефектности при разработке веро-

ятностной модели исходили из того, чтобы начальный размер дефекта с дос-

таточно большой вероятностью не превышал максимально допускаемого по

нормам [48]. При этом в зависимости от требуемой достоверности результа-

тов схематизации получают различные значения количественных параметров

дефектов.

Рис. 17. Геометрические схемы технологических дефектов

Анализ методов и алгоритмов моделирования (схематизации) дефект-

ности показывает, что все многообразие реальной дефектности сводится к

ограниченному числу расчетных схем, причем иногда без необходимого

обоснования. В связи с этим, располагая арсеналом численных методом ис-

следования напряженного состояния, целесообразно оценить влияние реаль-

ных форм, размеров и ориентации дефектов в элементах конструкций на рас-

пределение напряжений, сравнить получаемые результаты со стандартными

расчетными схемами и осуществить вероятностную интерпретацию полу-

чаемых результатов.

2.3. Статистические исследования параметров дефектности

Вероятностное моделирование дефектности предполагает наличие ис-

ходных статистических данных, проведение их обработки, установку формы

закона распределения и значений его параметров. Рассмотрим основные эта-

пы статистической обработки исходных данных по дефектности, предпола-

гая, что они получены по результатам неразрушающего контроля и представ-

лены в виде вариационных рядов параметров (длины трещины, диаметра,

длины, глубины залегания, площади технологического дефекта и т. д.).

Для подбора подходящего теоретического распределения прежде всего

следует построить экспериментальную кривую плотности распределения, по-

сле чего визуально выбрать похожую кривую из известных типов теоретиче-

ских распределений. При построении экспериментальной кривой данные

ранжируют в порядке возрастания, разбивают на группы, строят гистограм-

му, а по ней – экспериментальную кривую. Разумеется, что при наличии ос-

нований отдать предпочтение тому или иному теоретическому закону рас-

пределения необходимость в построении экспериментальной кривой отпада-

ет.

Выбрав тип предполагаемого теоретического распределения, выдвига-

ют нулевую гипотезу о взаимном соответствии теоретического и экспери-

ментального распределений, проверяют ее на заданном уровне значимости,

используя критерии согласия.

При больших выборках (n > 100) предпочтение следует отдавать кри-

терию согласия Пирсона. Иногда этот критерий используют при сущест-

венно меньших выборках. Критерий Колмогорова – Смирнова дает хорошие

результаты при n > 30 и удовлетворительные при 100 > n > 10. При n < 10

лучшие результаты дает критерий Крамера – фон Мизеса. Эти рекомендации

весьма приблизительны, так как каждый из критериев имеет свои сильные и

слабые стороны, и относительно выбора между ними можно дать лишь са-

мые общие указания.

Критерий Пирсона (хи-квадрат) применим только к сгруппированным

данным. Рекомендуется, чтобы численность каждой группы (интервала) была

не меньше 5. Если это не так, то смежные малочисленные группы следует

объединять с соседними.

Разбив исходные данные на т интервалов (групп), для каждого интер-

вала вычисляют:

экспериментальные частоты р

= n

/n, где n

– количество данных, по-

павших в i-й интервал, n – общее количество данных (объем выборки);

теоретические частоты p

=Ф(x

i+1

) – Ф(x

), найденные по таблицам или

формулам для выбранного типа теоретического распределения;

экспериментальную величину

 









 

 









npn

1 1

По таблицам квантилей распределения χ

(табл. П1) при заданном

уровне значимости β (обычно 5 %) и известном числе степеней свободы f на-

ходят теоретическое значение χ

. Число степеней свободы f равно количеству

интервалов минус число независимых условий (связей), наложенных на экс-

периментальные частоты р

. Примерами таких условий могут быть: равенст-

во единице суммы всех частот (такое условие накладывается всегда), совпа-

дение статистического среднего с гипотетическим, совпадение дисперсий

и т. п. Следовательно, f = m – 1 – r, где т – число интервалов, 1 – отмеченное

выше условие, r – число параметров, определяемых из опытных данных. Так,

если предполагаемое распределение нормальное, то оценивают два парамет-

ра (математическое ожидание и среднее квадратическое отклонение), поэто-

му f = m – 1 – r = m – 1 – 2 = m – 3; при распределении по закону Пуас-

сона, содержащему лишь один параметр λ, будем иметь r = 1, поэтому

f = m – 1 – 1 = m – 2. Если дополнительные условия (кроме первого) не на-

ложены, то f = m – 1.

При выполнении условия







считают, что при заданном уровне значимости (β = 5 %) функция распреде-

ления согласуется с экспериментальными данными.

Более жесткие требования по уровню значимости следует выдвигать с

осторожностью. Увеличение доверительной вероятности уменьшает вероят-

ность того, что незначимое различие будет принято за значимое и правильная

функция будет отвергнута. Однако это увеличивает вероятность того, что

значимое различие будет принято за незначимое, т. е. кривая, в дейст-

вительности не подходящая к данным наблюдениям, будет принята за подхо-

дящую. Вероятность последнего события можно оценить только в том слу-

чае, если будет высказана какая-нибудь альтернативная гипотеза.

Во избежание возможных ошибок первого и второго рода, в особенно-

сти если согласование теоретических и эмпирических частот «слишком хо-

рошее», следует проявлять осторожность. Например, можно повторить опыт,

увеличив число наблюдений, воспользоваться другим критерием согласия,

вычислить асимметрию и эксцесс и сопоставить их с известными для данного

распределения.

Критерий Колмогорова – Смирнова определяют разностью макси-

мальных абсолютных значений статистической функции распределения F*(х)

и соответствующей теоретической функцией распределения F(x), т. е.









xFxFD 

max

Н. В. Смирновым, а затем А. Н. Колмогоровым было доказано, что ка-

кой бы вид ни имела функция F(x), при неограниченном возрастании числа

независимых наблюдений п вероятность неравенства

nD

стремится к пределу

   











Для практического использования критерия составлена таблица кван-

тилей (табл. П2), определенных из соотношения k(λ

) = α, где функция рас-

пределения записана в ином виде

   













121 ek

Схема применения критерия Колмогорова – Смирнова следующая.

По результатам п наблюдений строят (рис. 18) статистическую функ-

цию распределения F*(х).

На тот же график наносят предполагаемую теоретическую функцию

распределения F(x).

Определяют максимальную величину модуля разности ординат D и

вычисляют величину

nD .

С помощью табл. П2 по заданному уровню значимости β (доверитель-

ной вероятности α) находят значение λ

. Если λ < λ

, то теоретическое и экс-

периментальное распределения согласуются на заданном уровне значимости.