Доронин С.В., Бабушкин А.В. Механика разрушения. Разрушения и дефектность технических систем
Подождите немного. Документ загружается.

51
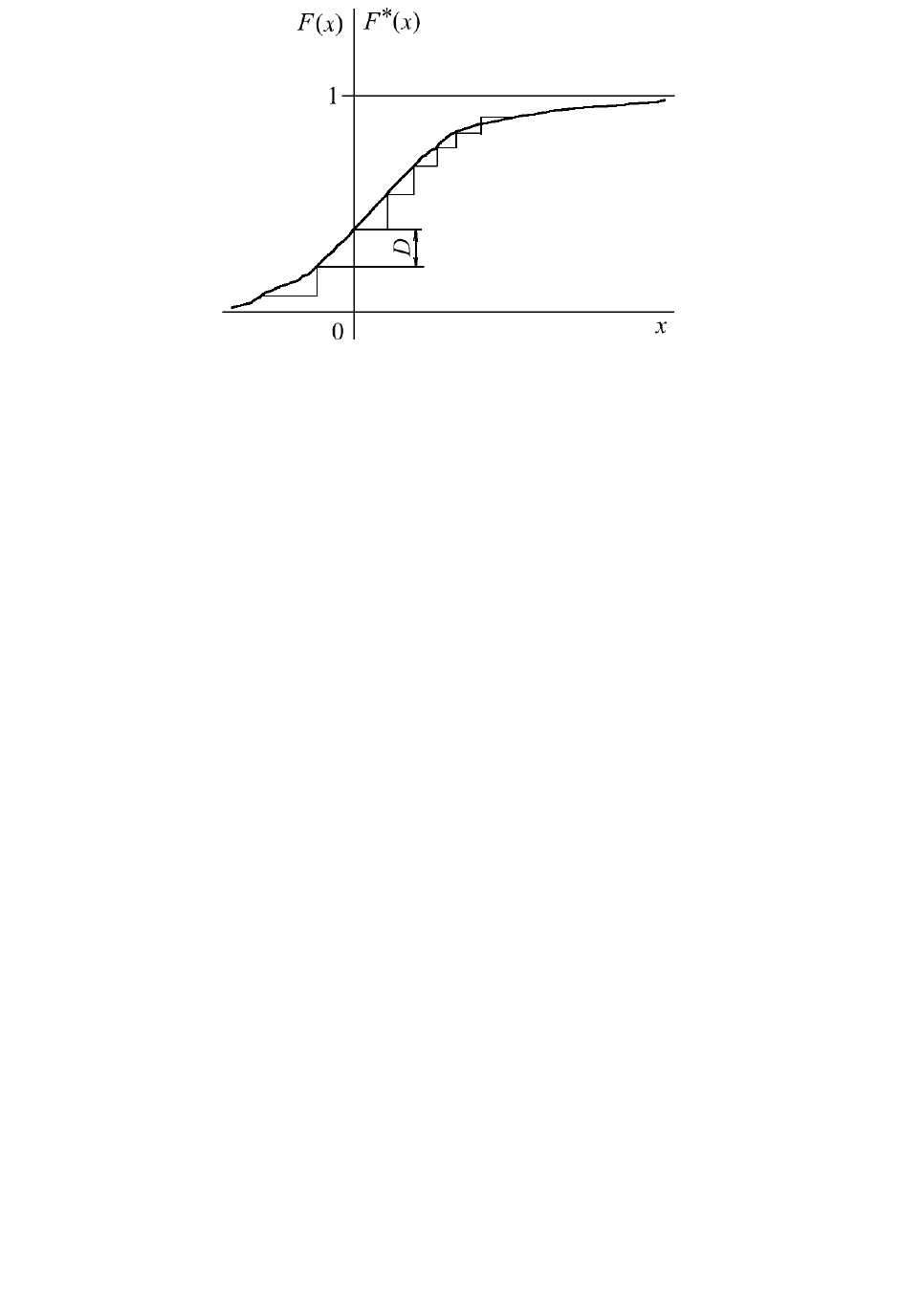
Рис. 18. Статистическая функция распределения
Пример подбора подходящего теоретического распределения.
Пусть задан массив случайных чисел х
1
, х
2
, x
3
, ..., х
n
. Требуется определить
теоретическое распределение этих чисел.
Рассмотрим все операции на конкретном примере. В качестве исходно-
го вариационного ряда взят массив диаметров технологической дефектности
вал-шестерен, полученный по результатам неразрушающего контроля. Ис-
ходный массив для секции вала диаметром 460 мм и длиной 315 мм записан в
табл. 2.
Прежде всего массив случайных величин x
i
следует выстроить в поряд-
ке возрастания значений случайных величин (ранжировать) с указанием,
сколько раз такое значение повторяется. Проделав эти операции, можно за-
писать протокол упорядоченной статистической совокупности (табл. 3).
Далее следует разделить весь диапазон изменения случайных величин
(в нашем случае 0,7–13,7) на отдельные интервалы, определить их количест-
во и назначить ширину интервалов.
Количество интервалов назначают с учетом точности дальнейших по-
строений, которая, в свою очередь, зависит от размера массива случайных
величин. Такой массив может состоять из многих сотен элементов и более.
Так, при имитационном моделировании работы конструкций число прогонов
модели, следовательно, количество выходных данных может измеряться де-
сятками тысяч. При больших массивах случайных величин количество ин-
тервалов выбирают порядка 12–20. При физическом моделировании каждый
эксперимент связан со значительными экономическими, временными, техни-
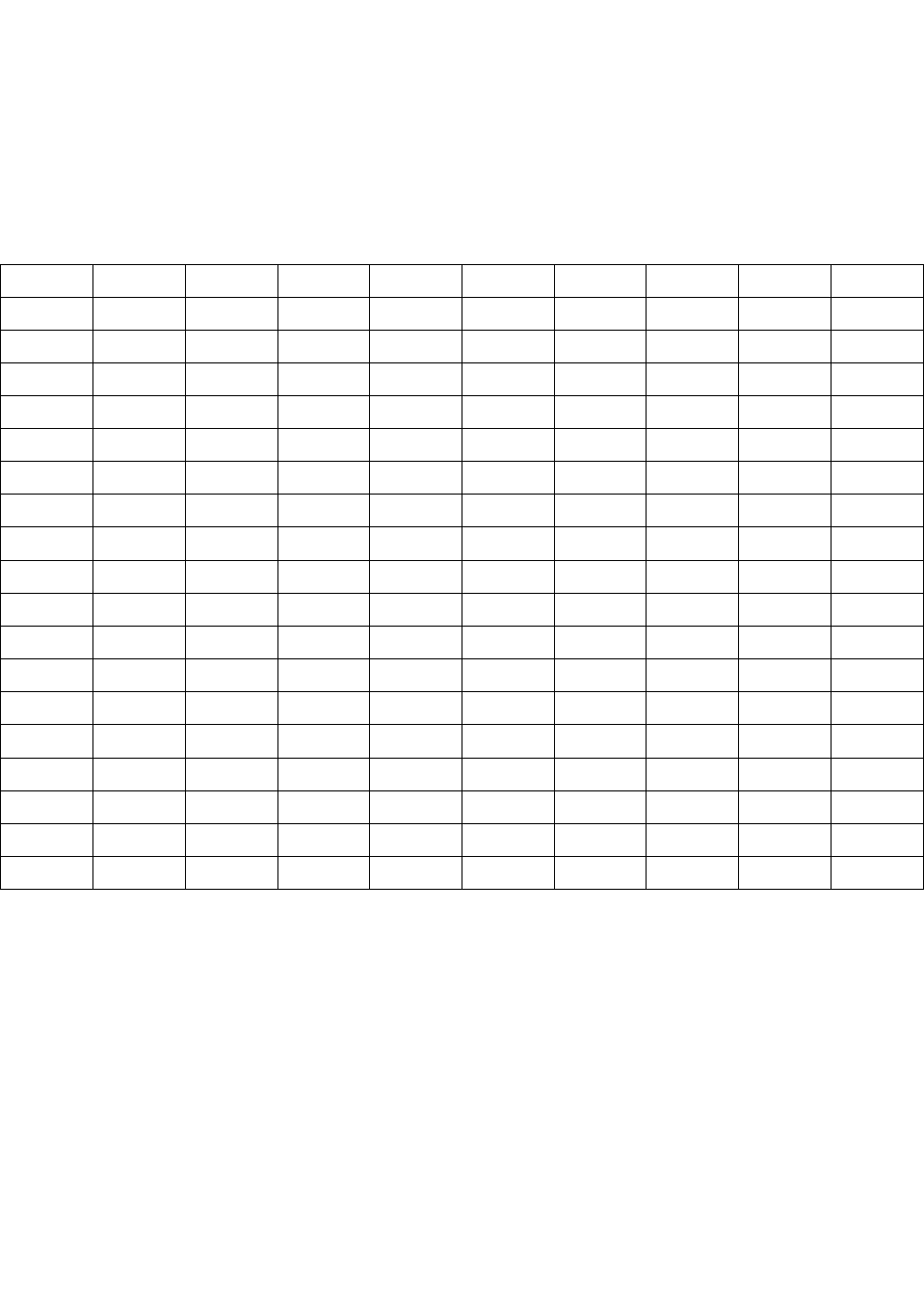
52
ческими затратами, поэтому число выходных данных измеряется десятками.
В этих условиях не имеет смысла принимать большое количество интерва-
лов, можно ограничиться 6–12.
Таблица 2
Исходный статистический массив
№ п/п x
i
№ п/п x
i
№ п/п x
i
№ п/п x
i
№ п/п x
i
01 2,9 19 3,1 37 11,1 55 2,1 73 0,7
02 3,0 20 2,8 38 5,4 56 2,2 74 5,2
03 4,9 21 4,5 39 2,1 57 2,8 75 2,0
04 2,0 22 2,6 40 1,5 58 4,2 76 2,1
05 1,6 23 3,0 41 2,2 59 3,6 77 0,9
06 2,8 24 3,4 42 2,3 60 1,7 78 2,0
07 2,8 25 3,8 43 1,8 61 1,3 79 2,8
08 4,1 26 7,1 44 1,0 62 4,7 80 1,9
09 2,1 27 7,1 45 1,6 63 2,1 81 2,8
10 2,0 28 1,9 46 13,7 64 2,6 82 2,3
11 5,1 29 2,2 47 2,6 65 1,7 83 3,2
12 3,7 30 2,6 48 5,9 66 2,3 84 2,7
13 4,2 31 2,5 49 8,3 67 1,9 85 2,3
14 3,7 32 3,1 50 6,3 68 1,9 86 3,0
15 3,1 33 2,0 51 3,3 69 2,5 87 2,7
16 2,8 34 3,0 52 1,8 70 2,2 88 2,6
17 5,9 35 5,5 53 2,1 71 3,6 89 3,4
18 3,6 36 8,3 54 2,9 72 6,0 90 2,7
Для удобства вычислений границы интервалов не должны быть дроб-
ными. Совершенно не обязательно принимать одинаковую ширину интерва-
лов: там, где значения случайных величин располагаются чаще, можно
уменьшать ширину интервала, а там, где реже – увеличивать.
В данном примере выбрано 13 интервалов.
Дальнейшие вычисления удобно проводить в табличной форме
(табл. 4). В первом столбце записаны номера интервалов, во втором – грани-
цы интервалов, в третьем – среднее значение интервала, в четвертом – коли-
чество случайных величин, попавшее в данный интервал. Их следует подсчи-
тывать по данным табл. 3. При этом, если случайные величины x
i
расположе-
53
ны на границе интервала, то половину из них относят к левому, и половину –
к правому интервалам.
Таблица 3
Упорядоченная статистическая совокупность
x
i
0,7 0,9 1,0 1,3 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2
n
i
1 1 1 1 1 2 2 2 4 5 6 4
x
i
2,3 2,5 2,6 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,6
n
i
4 2 5 3 7 2 4 3 1 1 2 3
x
i
3,7 3,8 4,1 4,2 4,5 4,7 4,9 5,1 5,2 5,4 5,5 5,9
n
i
2 1 1 2 1 1 1 1 1 1 1 2
x
i
6,0 6,3 7,1 8,3 11,1 13,7
n
i
1 1 2 2 1 1
Правила заполнения остальных столбцов понятны из их заголовков.
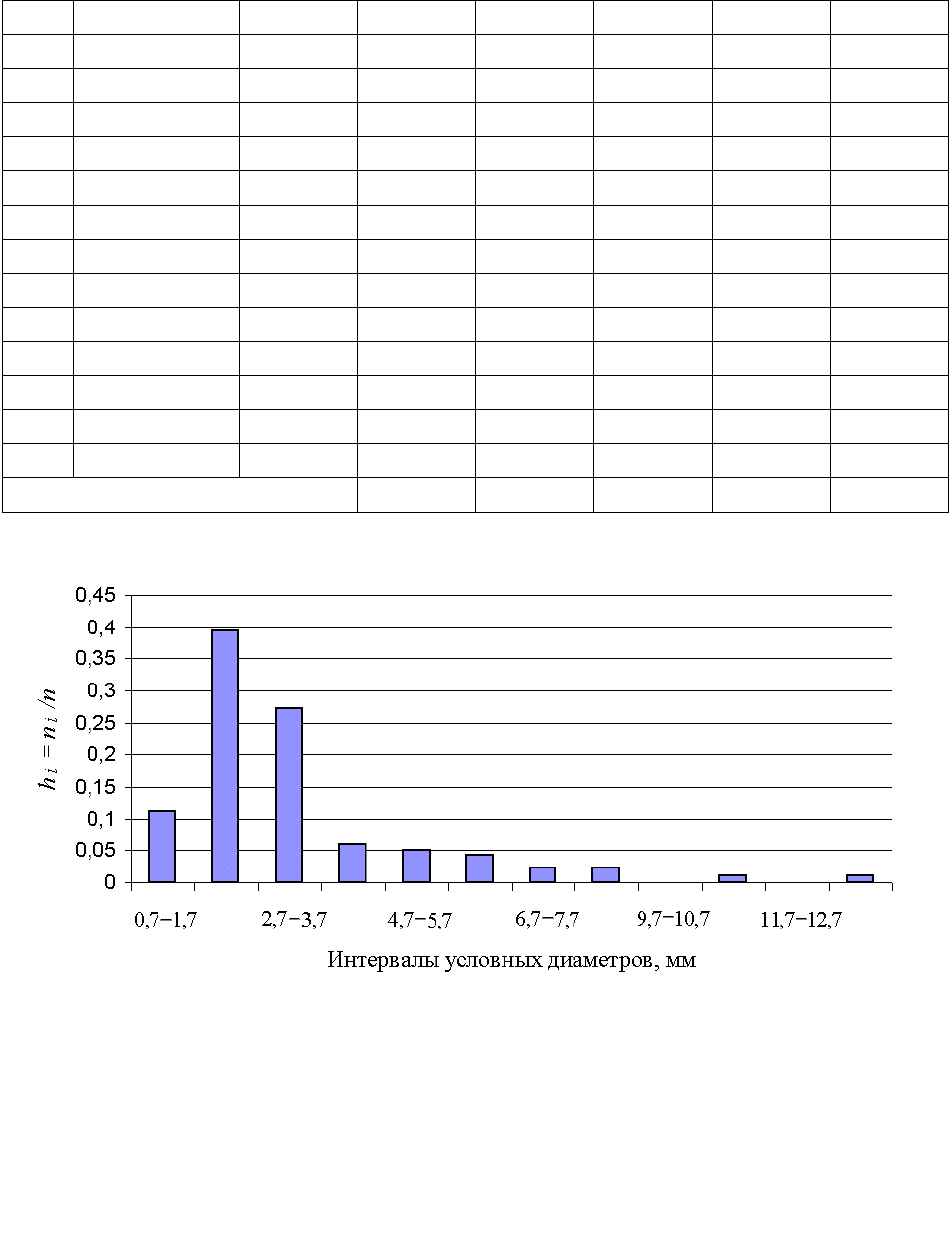
Полученные данные позволяют построить гистограмму (рис. 19), для
чего на оси абсцисс нужно отложить интервалы (второй столбец табл. 4), а на
оси ординат – частоты (восьмой столбец). Для построения эксперименталь-
ной плотности распределения ординаты гистограммы должны иметь значе-
ния h
i
/d (d – величина интервала). В этом случае площадь, ограниченная гис-
тограммой, будет равна единице. Соединив вершины столбиков линиями
(пунктирная кривая), найдем экспериментальную кривую плотности распре-
деления заданного массива случайных величин.
Следующий этап – подбор подходящего теоретического распределе-
ния. Главными факторами здесь являются внешнее сходство кривых распре-
деления по форме и закономерностей распределения – по своей сути.
Для того чтобы оценить сходство распределений по форме, нужно
сравнить построенную экспериментально кривую плотности распределения с
кривыми известных теоретических распределений.
Для оценки сходства распределений следует вникнуть в физический
смысл данного распределения или учесть накопленный опыт. Так, если рас-
сматривать равновероятные события, например фиксировать числа, выпав-
шие при игре в рулетку, лото и т. п., то следует ожидать равномерное рас-
пределение.
54
Таблица 4
Статистическая обработка
i Интервал x
i
n
i
x
i
n
i
x
i
2
x
i
2
n
i
h
i
= n
i
/n
1 0,7–1,7 1,2 10 12 1,44 14,4 0,111
2 1,7–2,7 2,2 35,5 78,1 4,84 171,82 0,394
3 2,7–3,7 3,2 24,5 78,4 10,24 250,88 0,272
4 3,7–4,7 4,2 5,5 23,1 17,64 97,02 0,061
5 4,7–5,7 5,2 4,5 23,4 27,04 121,68 0,05
6 5,7–6,7 6,2 4 24,8 38,44 153,76 0,044
7 6,7–7,7 7,2 2 14,4 51,84 103,68 0,022
8 7,7–8,7 8,2 2 16,4 67,24 134,48 0,022
9 8,7–9,7 9,2 0 0 84,64 0 0
10 9,7–10,7 10,2 0 0 104,04 0 0
11 10,7–11,7 11,2 1 11,2 125,44 125,44 0,011
12 11,7–12,7 12,2 0 0 148,84 0 0
13 12,7–13,7 13,2 1 13,2 174,24 174,24 0,011
Сумма 90 293 1300,6
Рис. 19. Гистограмма плотности распределения диаметра дефекта
Когда случайное событие является следствием многих причин при
примерно одинаковом вкладе каждой из них, логично ожидать нормальное
распределение. К такому распределению относят ошибки измерений, меха-
нические характеристики сталей, диаметры просверленных отверстий и т. п.
55
Логарифмически нормальное распределение характерно для продолжи-
тельности биологической жизни, образования индекса цен, времени износа
оборудования, распределения доходов и др.
Распределение Пуассона описывает редкие события, такие как количе-
ство дефектов в готовом изделии; количество аварий самолетов, автомоби-
лей, поездов, происшедших за отрезок времени; число требований выплаты
страховых сумм, поступающих в единицу времени.
Распределение Гумбеля находит применение в статистическом анализе
снеговых нагрузок.
Распределение Вейбулла хорошо описывает хрупкое разрушение мате-
риалов.
Все сказанное следует учитывать при выборе подходящего закона рас-
пределения на первом этапе. Окончательное суждение можно сделать только
после количественных оценок. Такие оценки делают на основе статистиче-
ских критериев согласия. Сравнив экспериментальную кривую с кривыми
известных распределений, проверим возможность использования для ее опи-
сания нормального закона распределения.
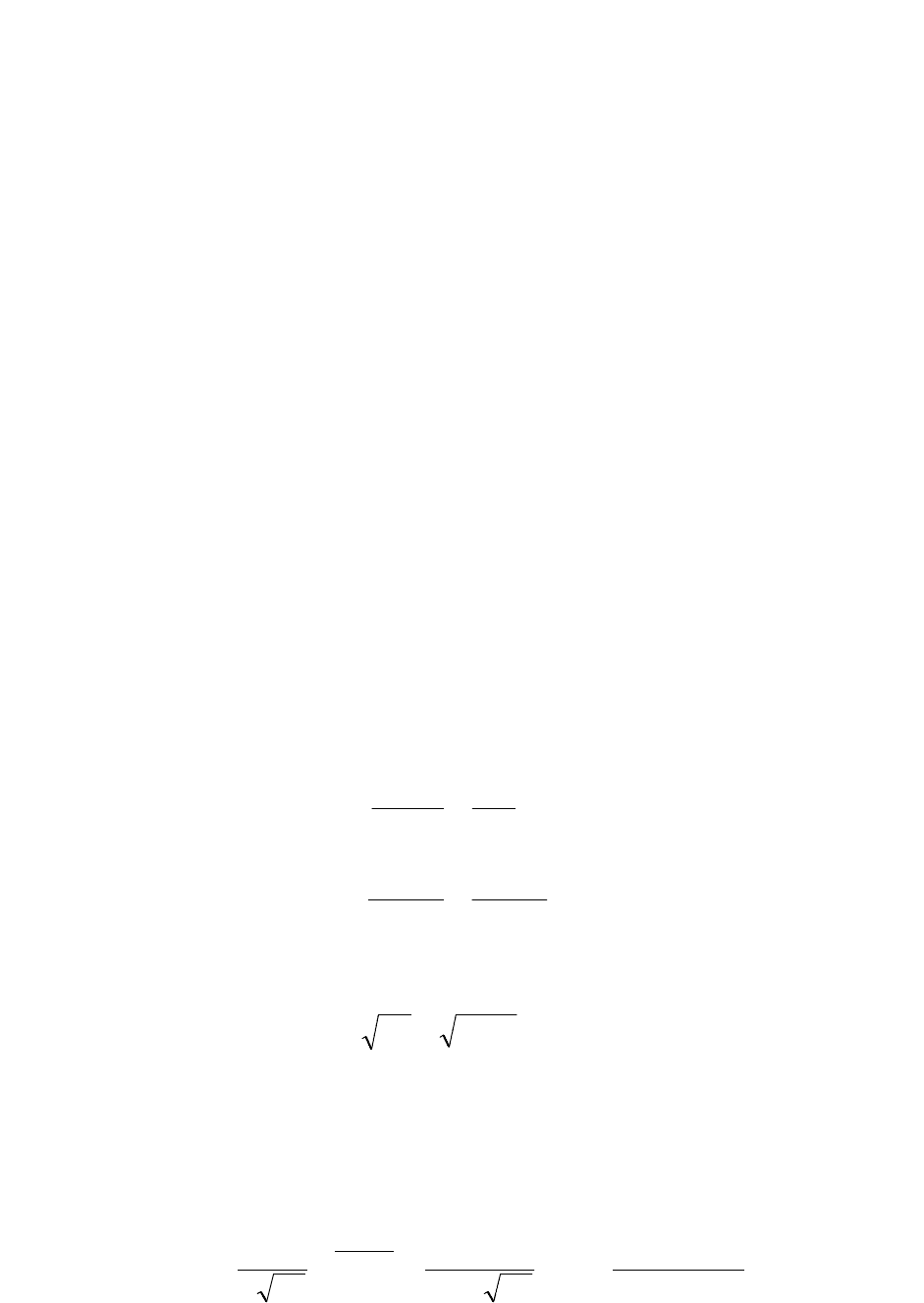
Прежде всего следует определить статистические параметры распреде-
ления по группированным данным (табл. 4)
,255,3
90
293
n
nx
m
ii
x
,451,14
90
1300,6
2
2
n
nx
xM
ii
,855,3595,10451,14
22
xx
mxMD
.964,1855,3
x
D
Если считать полученные значения т
х
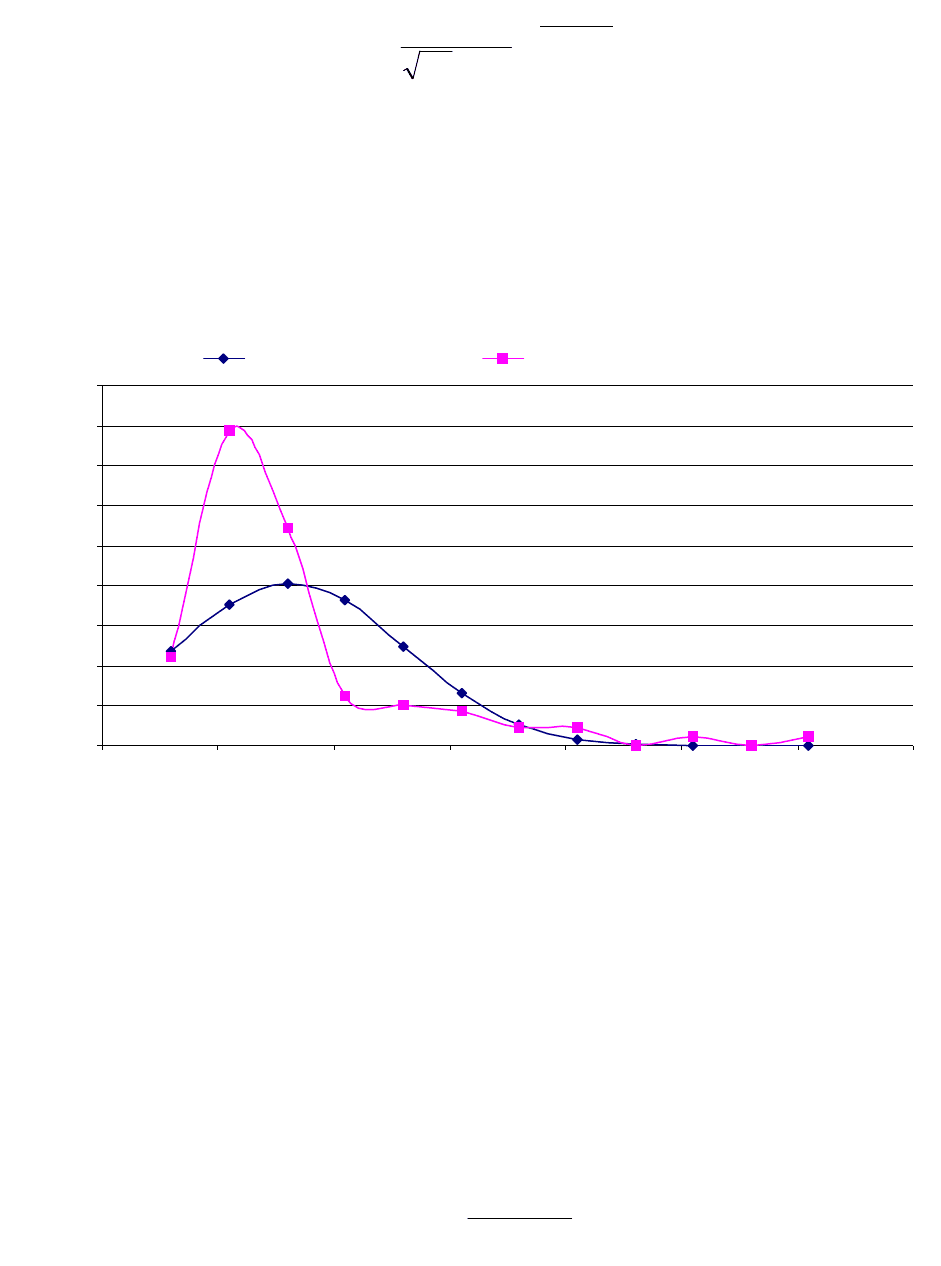
и σ точными, то величина х име-
ет плотность распределения
.
715,7
255,3
exp
2964,1
1
2
1
2
2
2
2
x
exf
x
mx
56
Эта плотность распределения соответствует функции распределения
x
t
dtexF
715,7
255,3
2
964,12
1
.
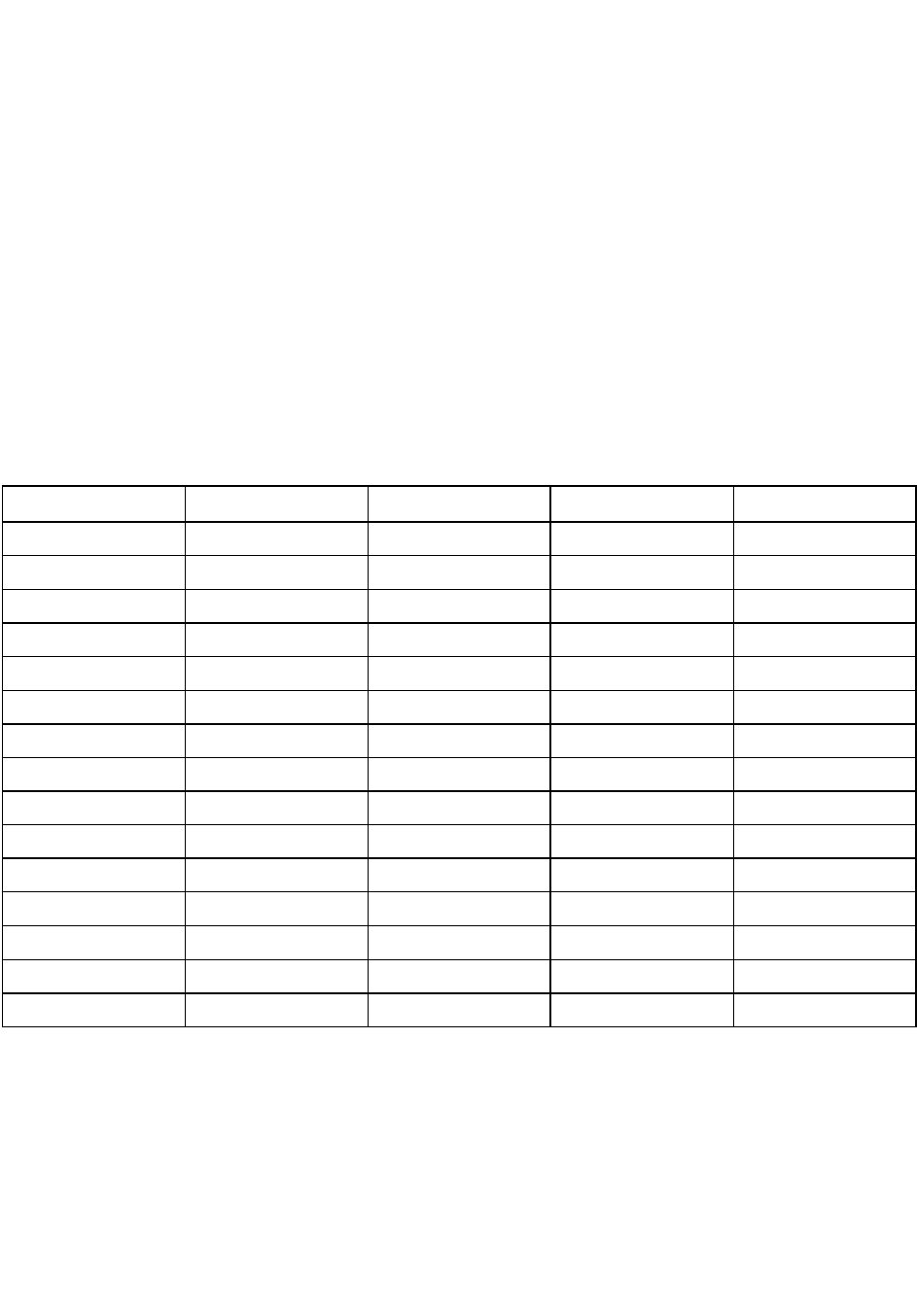
Построение теоретической и экспериментальной кривых плотности ве-
роятностей распределения диаметра дефекта (рис. 20) позволяет качественно
визуально оценить близость фактического распределения теоретическому
нормальному.
0
0,05
0,1
0,15
0,2
0,25
0,3
0,35
0,4
0,45
0 2 4 6 8 10 12 14
Условный диаметр дефекта, мм
h
i
= n
i
/n
Теоретическая Экспериментальная
Рис. 20. Теоретическая и экспериментальная кривые плотности распределе-
ния вероятностей
На этом закончен первый этап обработки экспериментальных данных.
Далее следует проверить возможность использования двух последних выра-
жений на основе критериев согласия.
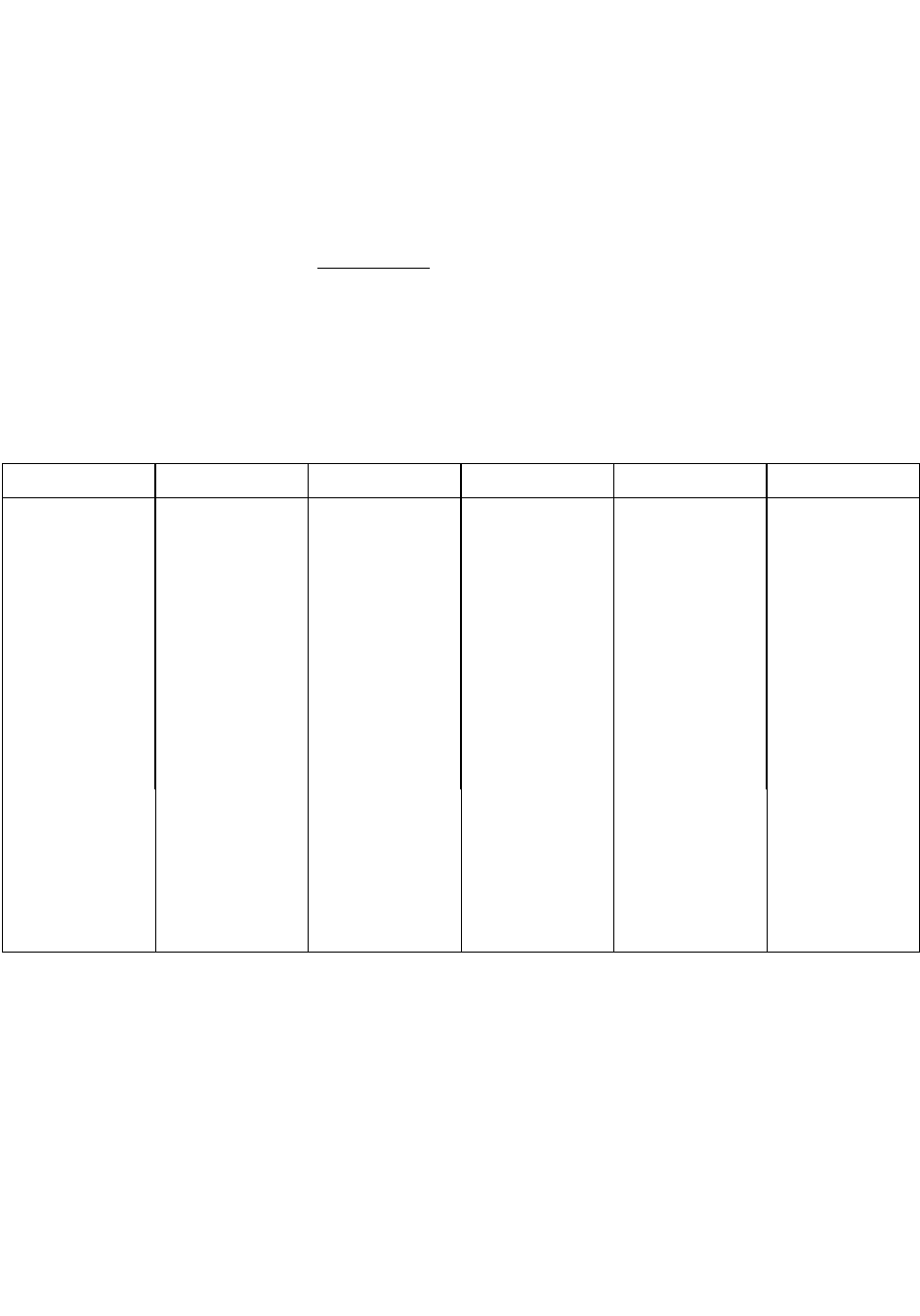
Критерий Колмогорова – Смирнова. Выразим функцию распределения
f(x) через нормированную нормальную функцию распределения
964,1
255,3x
x ,
57
что позволяет определить теоретические накопленные частоты p
i
по данным
табл. П3. При этом Ф(–х) = Ф(x); Ψ(–x) = 0,5 – Ф(х). Так, для второй строки
табл. 5 будем иметь: Ф(–2,5) = 0,4938; p
i
= 0,5 – 0,4938 = 0,0062 ≈ 0,006. Для
х > 0 накопленные частоты вычисляются как p
i
= 0,5 + Ф(x). Столбец 4 со-
держит экспериментальные накопленные частоты и последовательные суммы
частот h
i
(табл. 4).
Анализируя данные столбца 5 табл. 5, находим максимальную разность
теоретической и экспериментальной накопленных частот D = 0, 277. Опреде-
ляем λ=D√n = 0, 277 √90=6,628.
Таблица 5
Расчеты по критерию Колмогорова – Смирнова
x
I
(x
i
– m
x
)/
p
i
H
i
p
i
– H
i
0,7 –1,3 0,097 0 0,097
1,2 –1,046 0,159 0,111 0,048
2,2 –0,537 0,345 0,505 –0,16
3,2 –0,028 0,5 0,777 –0,277
4,2 0,481 0,692 0,838 –0,146
5,2 0,99 0,841 0,888 –0,047
6,2 1,499 0,933 0,932 0,001
7,2 2,008 0,977 0,954 0,023
8,2 2,517 0,994 0,976 0,018
9,2 3,026 0,9986 0,976 0,0226
10,2 3,536 0,9998 0,976 0,0238
11,2 4,045 0,99997 0,987 0,01297
12,2 4,554 0,999997 0,987 0,012997
13,2 5,063 0,9999997 0,998 0,0019997
13,7 5,318 1
По табл. П2 при уровне значимости 5 % ( = 0,95) λ
α
= 0,1412. По-
скольку λ > λ
α
, то по критерию Колмогорова – Смирнова разница между тео-
ретическим и экспериментальным распределениями является значимой и нет
оснований принимать гипотезу о нормальном распределении заданной сово-
купности.
Критерий Пирсона (χ-квадрат). Определим теоретические вероятности
58
попадания случайных величин в заданные интервалы. Вычисления сведены в
табл. 6. Столбец 2 табл. 6 заполняют на основании данных столбца 3 табл. 5.
Столбец 3 табл. 6 дублирует столбец 8 табл. 4. Смысл других данных табл. 6
ясен из заголовков столбцов.
Находим величину (χ
2
)*
.451,47155,0163590
2
*
2
i
ii
p
hp
n
Таблица 6
Расчеты по критерию Пирсона
Интервалы Δp
i
= p
i + 1
– p
i
h
i
=n
i
/n ∆p
i
–h
i
(∆p
i
–h
i
)
2
(∆p
i
–h
i
)
2
/∆p
i
0,7–1,7 0,186 0,111 0,075 0,005625 0,030242
1,7–2,7 0,155 0,394 –0,239 0,057121 0,368523
2,7–3,7 0,192 0,272 –0,08 0,0064 0,033333
3,7–4,7 0,149 0,061 0,088 0,007744 0,051973
4,7–5,7 0,092 0,05 0,042 0,001764 0,019174
5,7–6,7 0,044 0,044 0 0 0
6,7–7,7 0,017 0,022 –0,005 0,000025 0,001471
7,7–8,7 0,0046 0,022 –0,0174 0,00030276 0,065817
8,7–9,7 0,0012 0 0,0012 0,00000144 0,0012
9,7–10,7 0,00017 0 0,00017 2,9·10
-8
0,00017
10,7–11,7 0,000027 0,011 –0,010973 0,00012 4,444444
11,7–12,7 0,0000027 0 0,0000027 7,29·10
-12
2,7·10
-06
12,7–13,7 0 0,011 –0,011 0,000121 –
Σ 5,01635
Для семи степеней свободы (f = n – 3, так как по выборке оценивают
два параметра) находим по табл. П6 для уровня значимости 5 % значение
χ
2
= 14,1. Поскольку (χ
2
)* > χ
2
, можно считать, что согласно критерию Пирсо-
на анализируемые данные не соответствуют нормальному распределению.
Статистический анализ параметров дефектности позволяет утверждать
приемлемость использования распределений Вейбулла, логарифмически
нормального и экспоненциального для описания различных характеристик
дефектности. В связи с этим рассмотрим алгоритмы определения параметров

59
распределений по статистическим данным.
Оценка параметров распределения Вейбулла. Функция плотности
вероятности случайной величины Х, распределенной по закону Вейбулла,
описывается формулой
,,0
,,exp
1
x
x
xx
xf
где , , – параметры распределения.
Параметр имеет смысл наименьшего значения случайной величины
Х и может быть оценен как минимум рассматриваемого вариационного ряда.
В некоторых случаях параметр не требует статистической оценки, так как
минимальное значение случайной величины вытекает из каких-либо физиче-
ских соображений.
Параметры формы и масштаба могут быть определены следующим
образом. Вначале определяют параметр решением уравнения
,
21
11
2
2
2
2
xx
x
где
х
и
х
– статистические оценки среднего значения и среднеквадратиче-
ского отклонения вариационного ряда, Г(·) – гамма-функция. Далее параметр
определяют по формуле
.
11
x
Оценка параметров экспоненциального распределения. Функцию
плотности вероятности случайной величины Х, распределенной по экспонен-
циальному закону, описывают формулой

60
b
x
b
xf exp
1
.
Параметр b является математическим ожиданием случайной величины
Х и оценивается как среднее арифметическое рассматриваемого вариацион-
ного ряда.
Оценка параметров логарифмически нормального распределения.
Функцию плотности вероятности случайной величины Х, распределенной по
логнормальному закону, описывают формулой
2
2
2
lg
exp
2
1 mx
x
xf .
Параметр масштаба m является медианой, а параметр формы σ стан-
дартным отклонением случайной величины Х. Оценку этих параметров вы-
полняют с помощью преобразования соответствующих оценок для нормаль-
ного распределения по формулам
.lg
1
1
;exp;lg
1
1
2
1
n
i
i
n
i
i
x
n
mx
n
Вероятностные модели технологической дефектности крупногаба-
ритных кованых деталей. Рассмотрим в качестве примера технологическую
дефектность изготавливаемых из поковок типовых вал-шестерен, применяе-
мых в карьерных экскаваторах ЭКГ-12,5 производства ОАО «Красноярский
завод тяжелых экскаваторов». Это промежуточные вал-шестерни в тихоход-
ных редукторах главных приводов экскаватора. Они отличаются большими
габаритами и массой (диаметр 530 мм, длина 1322 мм, масса 1065 кг – вал-
шестерня 3535.09.03.211 (рис. 21); диаметр 460 мм, длина 1945 мм, масса
703 кг – вал-шестерня 3537.11.01.008 (рис. 22), содержат несколько ступеней
различной длины и диаметра, изготавливаются из сталей 34ХН1МА,
34ХН3МА.
