DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.

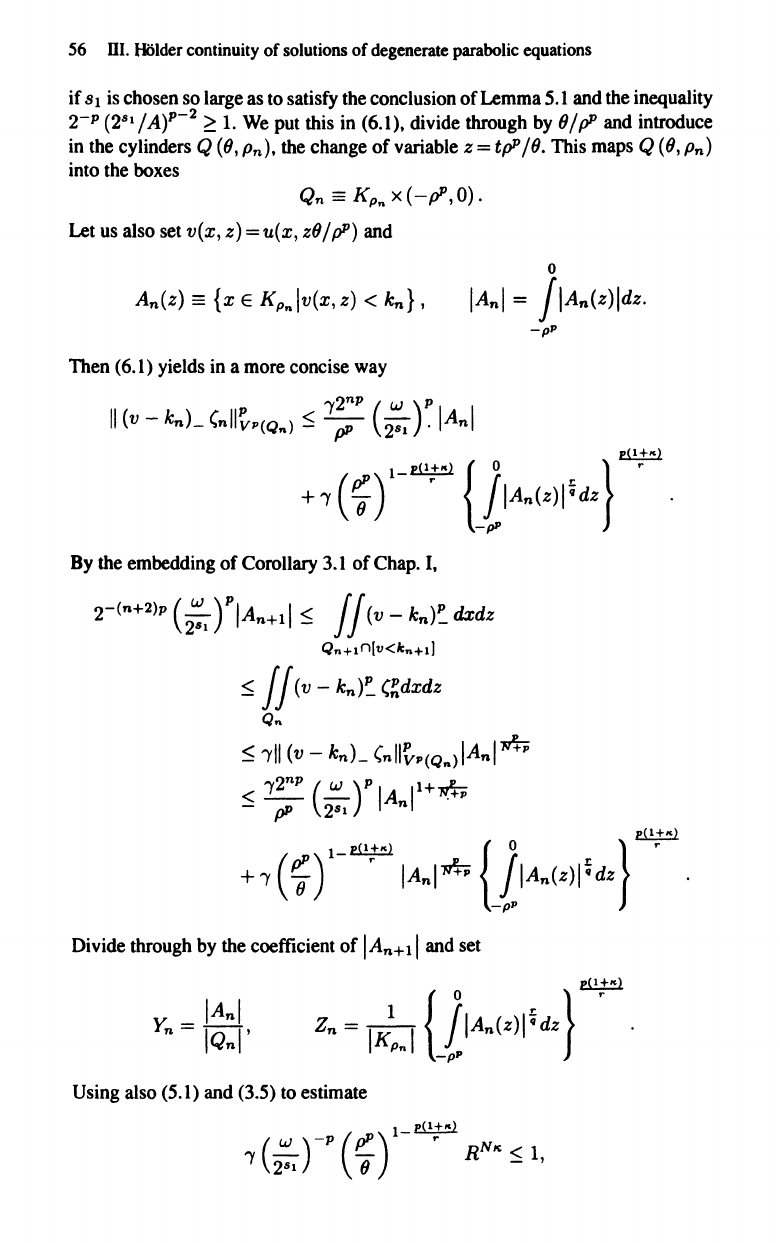
56
DI.
HOlder
continuity of solutions of degenerate
parabolic
equations
if
81
is
chosen so large
as
to
satisfy the conclusion of Lemma
5.1
and the inequality
2-
P
(2
81
I A)p-2
~
1.
We
put this
in
(6.1), divide through
by
B I
pP
and
introduce
in
the cylinders Q
(B,
Pn),
the
change
of
variable z =
tPP
lB. This
maps
Q
(B,
Pn)
into the
boxes
Qn
==
KPn
x(-PP,O).
Let
us
also set v(x, z) = u(x,
zB
I
PP)
and
o
IAnl
=
jIAn(z)ldZ.
By
the embedding of Corollary 3.1 of
Chap.
I,
2-(n+2)1'
(2~1
)"IAn+l1
~
jj(v
-
kn)~
dxdz
Qn+1n[v<kn+11
~
jj(v
-
kn)~
(~dxdz
Qn
~
111
(v
-
knL
(nll~p(Q,,)IAnlwT,;
< 1
2n1'
(~)p
IA
Il+~
-
pP
2
8
1
n
-pP
I!i!±!!l
+~(~t"¥"
1A.lm
{}An(Z>li
dz
} •
Divide through
by
the coefficient of I
An+
11
and set
Using
also (5.1) and (3.5)
to
estimate

6.
The
first alternative
concluded
57
we
arrive
at
Y
n
+1
:5
-y4
np
{y~+m:;;
+
Yn;vT,;
Z~+/(
} .
Proceeding
as
in
the proof of Lemma 4.1,
we
have
Zn+1
:5
-y4
np
{Y
n
+
Z~+/(}.
By
Lemma 4.2 of Chap. I it follows that Y
n
and
Zn
tend
to
zero
as
n
-+
00,
provided
(6.2)
where
9
0
= min
{NT,;
j
K}.
To
prove the lemma,
we
fix
III
as
in
(6.2) and pick
81
according
to
Lemma 5.2.
We
summarise the results obtained so
far.
PROPOSITION
6.1.
There
exists
numbers
11
0
,
TJo
E (0,
1)
and
Al
» 1
depending
only
upon
the
data
and
indepeiuJent
o/w, R,
such
that if/or
some
cylinder o/the
type
[(0,
l)
+ Q
(dRP,
R»),
(6.3)
I(X,
t) E
[(0,
l)
+ Q
(dRP,
R)llu(x, t) <
jJ-
+
2~o
I
:5
1I
0
IQ(dRP,R)
I,
then
either
(6.4)
or
(6.5)
essosc
u:5
TJo
W
Q(d(
I)".f)
where
b
is
introduced
in
(3.4).
PROOF:
Assume (6.4)
is
violated.
By
Lemma 6.1,
we
can determine a positive
number
81
such that
.f
W
essm u >
jJ-
+--
Q(
8,-f)
- 2
81
+1
where
9 satisfies (5.1) with p = R/2. Change
the
sign of this inequality and
add
the quantity esssu
P
Q
(8.i) u
to
the left hand side and
jJ+
to
the right
hand side.
This gives
ess
OBC
U
:5
(1
-2
1+1)
w.
Q(8.f)
81
Therefore the proposition follows with
TJo
=
(1
-
2.:+1),
since

58
m.
IIUder continuity of
solutions
of degenerate
parabolic
equations
Remark
6.1.
Let
us
trace
the
dependence of
"10
and
Al
upon
lIulloo,nT.
The
num-
bers
Vo
and
VI
depend only
upon
the data and
are
independent of
u.
The number
81
is
given
by
81
= 8
0
+ n where n
is
chosen
from
(5.4). Thus
depends
upon
lIulloo.nT
via 8
0
through
(3.2).
Also A and
Al
are
of
the
type
Ai
=
2
so
+
h
"
where hi, i =
0,
1,2,
...
,
can
be
determined a priori only
in
terms of the
data
and
are
independent of
II
u
II
OO,nT.
We
conclude that if the lower order terms
b(x, t, u, Du) satisfy the structure condition (Aa) of§5 of Chap.
II,
we
have 8
0
= 1
and therefore
"10'
A,
Ai
can
be
determined a priori only
in
terms of
the
data
and
are
independent of
lIulloo,nT.
7.
The second alternative
We
assume
in
this section that the assumptions of
Lemma
4.1
are
violated, i.e.
for
every
subcylinder
[(0,
t) + Q
(dRP,
R)]
cQ
(aom', R)
I(X,t)
E
[(O,t)
+Q(dm',R)]lu(x,t)
< p.- +
2~o
I>
volQ
(dRP,
R)
I·
Since
we
rewrite this
as
(7.1)
I(X,
t) E [(0, t) + Q
(dRP,
R)lI
u
(x, t) >
p.+
-
2~o
I
~
(1-
v
o
) IQ(dRP,R)
I,
valid/or all cylinders
[(0,
t) + Q
(dRP,
R)]
c Q
(aoRP,
R)
~
=
(~)P-2.
a
o
A
In
view
of
(7.1)
we
will study the behaviour of u near its
supremum
p.
+ and
will
be
working
with
the truncated functions (u - k) +
for
the levels
i
~
0.
LEMMA
7.1. Let
[(0,
t) + Q
(dRP,
R)]
cQ
(aom', R) befixedand
let
(7.1)
hold.
There
exists
a
time
level
such
that

7. Tho second alternative 59
PROOF:
If
not,
for
aU
tE
[i -
dJlP,
i -
~dJlP],
and
Ix
E
KR
I
u(x,t)
>
p.+
-
2~0
I>
(11_-
v
:
i2
)
IKRI
I(X,
t)
E [(O,t) + Q
(dJlP,
R)]I u(x, t) >
p.+
-
2~0
I
t-!f-dRP
~
f
Ix
E
KR
I u(x,
r)
>
p.+
-
2~0
I dr
t-dRP
>
(I-va)
IQ(dRP,R)
I,
contradicting (7.1).
The lemma asserts that at some time level
t*
the set where u is close to
its
supremum occupies only a portion of the cube K
R.
The next lemma claims that this
indeed occurs
for
all time levels near the top of the cylinder
[(0,
t) + Q
(dJlP,
R)].
LEMMA
7.2.
There
exists a positive integer
82
> 8
0
such
that
Ix
E
KR
I
u(x,t)
>
p.+
-
2~21
:5
(1-
(~f)
IKRI,
for
a/ltE
[i -
~dJlP,
fj.
PROOF:
Consider the logarithmic inequalities (3.14) of Chap.
II
written over
the
box
K R X (t* , t)
for
the function (u -
k)
+ for the levels k =
p.
+ -
2":0
.
As
for the
number
c
in
the
definition of the function
1[1,
we
take
w
c---
- 2
B
o+n'
n > ° to be chosen.
Thus
we
take
(7.2)
where
Ht
==
ess sup u -
p.+
- - .
(
(
W
))
[(O,f)+Q(dRP
,R)]
2
80
+
The
cutoff function
x--+(x)
is
taken so that ( = 1
in
the cube
K(l-O')R,
uE
(0,
I),
and
ID(I:5 (UR)-l.
With
these choices, inequality (3.14) of Chap.
II
yields
for
all
tE(t*,t)
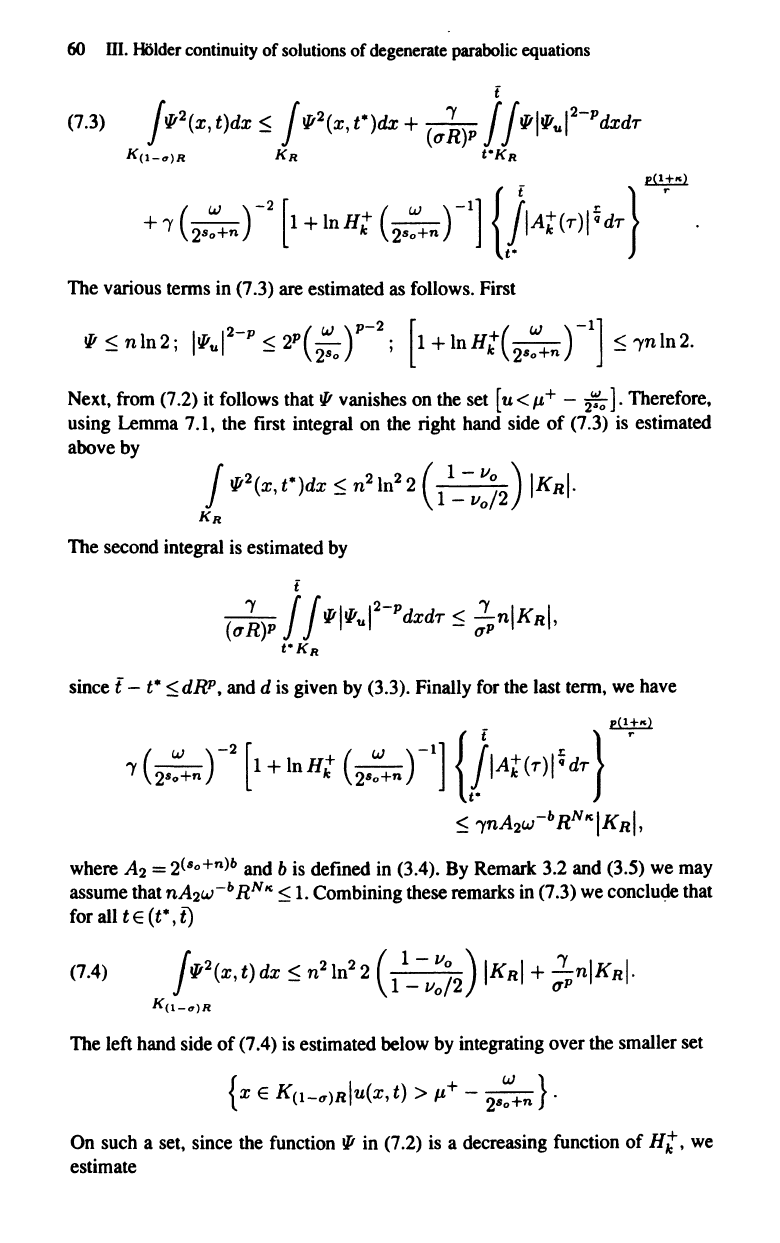
60
m.
HiUder
continuity
of
solutions
of degenerate
parabolic
equations
t
(7.3) I
p
2(X,t)dx:5 j llf2(x,to<)dx+
«(1~)P
j j
llf
lllf
u
l
2
-
P
dxdT
K(l-,,)R
KR
tOKR
E1.!±.!!.l
+ 0
(2'~+')
-2
[1
+
I.
Hi
C.~"")
-1]
{}At(Tl11dT}
·
The various tenns
in
(7.3) are estimated
as
follows. First
2 ( W
)P-2
[ ( W
)-1]
llf:5nln2;
Illf
u
l-
P
:5
2P
2"0
;
l+lnHt
2"0+n
:5-ynln2.
Next,
from
(7.2) it follows that
llf
vanishes on the set
[u<JL+
-
2":0].
Therefore,
using Lemma 7.1, the first integral
on
the right hand side of (7.3)
is
estimated
above
by
The second integral
is
estimated
by
t
«(1~)P
f f llflllfuI2-PdxdT:5
;pnIKRI,
tOKR
since f -
to<
:5dRP,
and d
is
given
by
(3.3). Finally
for
the last tenn,
we
have
E1.!±.!!.l
o
(2'~+.r'
[1+
I.Ht
(2.:'+.r']
{jIAt(Tl11dr}
·
:5
-ynA
2
w-
b
RNItIKRI,
where
A2
=
2(B
o
+n)b
and
b
is
defmed
in
(3.4).
By
Remark 3.2
and
(3.5)
we
may
assume that
nA2W-b
RNIt
$1.
Combining these remarks
in
(7.3)
we
conclu(,ie
that
for all
tE
(to<,
f)
(7.4) j llf2(x,
t)
dx
:5
n
2
1n
2
2
(11_-II:i2)
IKRI
+
;P
nIKRI·
K(1-,,)R
The left hand side of (7.4)
is
estimated below
by
integrating over the smaller set
{x
E
K(1-<T)Rlu(x,
t) >
1'+
-
2B~+n
} .
On
such a set, since the function
llf
in
(7.2)
is
a decreasing function of
Ht,
we
estimate
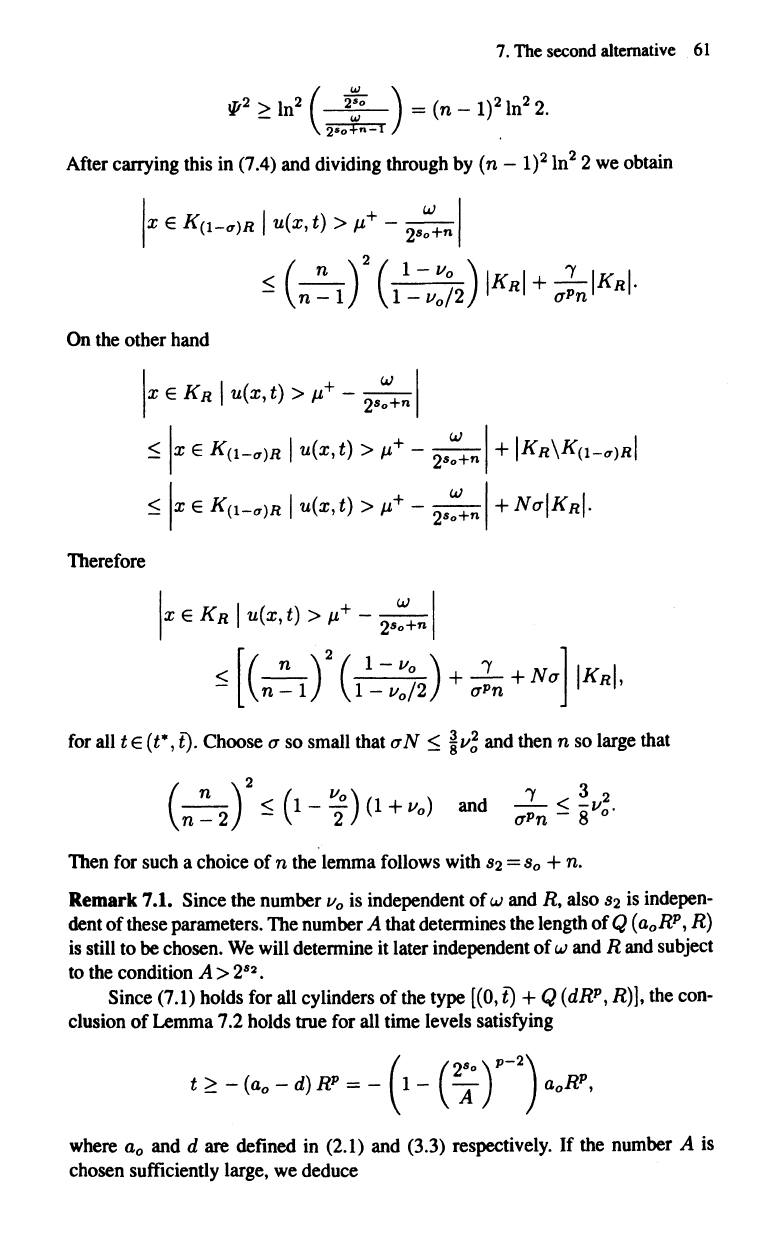
7. The second alternative
61
After carrying this
in
(7.4) and dividing through by (n - 1)21n
2
2
we
obtain
Ix E
K(l-u)R
I u(x,
t)
>
J1.+
-
2s~+n
I
~
(n:
lr
(/--V:/2)
IKRI
+
u;n
IKR1
·
On
the
other hand
Ix
E
KR
I
u(x,t)
>
J1.+
-
28~+n
I
Therefore
~
Ix
E
K(l-u)R
I u(x, t) >
J1.+
-
2s~+n
1+
IKR\K(l-u)RI
~
Ix
E
K(l-u)R
I u(x,
t)
>
J1.+
-
2B~+n
1+
NuIKRI·
Ix
E
KR
I u(x, t) >
J1.+
-
2s~+n
I
~
[(n:
1)
2
(/--v:i2)
+
u;n
+
NujIKRI,
for
all
t E (
t*
,
f).
Choose u
so
small that u N
~
~
v~
and then n so large that
Then for such a choice of
n
the
lemma follows with
82
= 8
0
+
n.
Remark
7.1. Since the number
Vo
is
independent of w
and
R, also
82
is
indepen-
dent of these parameters. The number
A that determines the length of Q
(aoRP,
R)
is
still to be chosen.
We
will determine it later independent of w and R
and
subject
to
the
condition A >
2B2
•
Since (7.1) holds for all cylinders of the type
[(0,
f)
+ Q
(dRP,
R)],
the
con-
clusion
of
Lemma 7.2 holds true for all time levels satisfying
where
a
o
and d are defined
in
(2.1) and (3.3) respectively. If the number A
is
chosen sufficiently large,
we
deduce

62
m.
ltilder continuity of solutions of degenerate puabolk: equations
COROLLARY 7.1.
ForalltE(-!fR",O),
From
now
on
we
will
focus
on
the cylinder Q
(!f
R",
R)
and
to simplify
the
symbolism
we
set
A.(t)
=
{x
E KRlu(x, t) >
J.I.+
-
;.
} ,
As
=
{(x,t)
E Q
(~
W,R)
lu(x,t)
>
J.I.+
-
;.}.
8.
The second alternative continued
The infonnation of Corollary
7.1
will
be employed to
deduce
that the set
where
u
is
close to its
supremum
J.I.+,
within
the
cylinder Q (!fRP,
R),
can
be
made
arbitrarily
small.
In
this section
we
will
also detennine the
length
of
the
cylinder
Q
(aoW,
R)
by
determining the number A.
LEMMA 8.1.
For
every
ZI. E (0,
1)
there
exists
a
IlUlltber
8.
>
82
independent
of
w and R,
such
that
Remark 8.1.
Assume
for
the
moment
that the
number
B.
has
been
chosen.
Then
we
determine
the
length of the cylinder Q (aoR" ,
R)
by choosing
(8.1)
PROOF
OF
LEMMA 8.1: Consider the local eneqy estimates (3.8) of
Chap.
II
written over
the
box
Q
(aoW,
2R),
for
the
functions
(u - k)+.
The
levels k
are
given
by
w
k=,,+--
,..
2·'
where
82
:::;
8
:::;
B.
and
B.
is
to
be chosen.
We
take a cutoff
function
( that equals
one
on
Q
(~W,
R), vanishes
on
the
parabolic
boundary
of
Q
(aoRP,
2R)
and
such
that
Neglecting
the
first
term
on
the left
hand
side
of
these
energy estimates,
and
using
the
indicated choices,
we
obtain

8. The second alternative continued
63
(8.2)
IIID(U-k)+IPdxdT~;;'
II(U-k)~dxdT
Q(.y.RP,R)
Q(a
o
RP,2R)
~
+
aO~
II(U-k)!dxdT+'Y{
JIAt.2R(T)lidT}
r
Q(a
o
RP,2R)
-a';RP
The various tenn on the right hand side
of
(8.2) are estimated as follows. First
(i)
;;,
II(U-k)~dxdT~
;P
(;rIQ(~RP,R)
I·
Q(a
o
Rp,2R)
Next by virtue
of
the choice (8.1)
of
the parameter A, and the defmition (2.1)
of
a
o
,
(ii)
ao~
If
(u -
k)!
dxdT
~
;"
(;
r
IQ
C;
R",
R)
I·
Q(a
o
RP,2R)
Finally making use
of
Remark 3.2 and (3.5)
~
(iii)
~
{j~At.2R(T)I\dT}
· .
~
;"
(;r
IQ
(~
R",R) I
(A
3
w-
b
R
NK
)
~;"
(;rIQ(~RP,R)
I,
where
A3
= 2
b8
• and b is defined in (3.4). These estimates in (8.2) give
(8.3)
fflDulPdxdT
~
;"
(;r
IQ
(~
RP,R)
I·
A.
Next we use Lemma 2.2
of
Chap. I applied
to
the function u(·,
t)
for all times
-!f
RP
~
t
~
0, and for the levels
w
(I
- k) = 2
8
+1
.
Notice that by virtue
of
Corollary 7.1 we have
Applying Lemma 2.2
of
Chap. I in this setting, gives

64 III. RUder continuity
of
solutions
of
degenerate parabolic equations
w
4-yR
N
H J
2S+1IAs+1(t)1
:5
v~
IKRI
IDul
dx,
A.(t)\AO+l
(t)
for all t E ( -
~
flP ,
0).
From this, integrating over such a time interval we get
2:1
lAsH
I
:5
~
R J J
IDul
dxdr
A.\A'+1
1
,;
~R
([fIDU1PdxdT)
'IA,\A.+d7'.
Take the ;tr power, estimate the integral on the right hand side by (8.3) and divide
through by
(2;+1
)
~
. This gives
IAs+1l~
:5
-y(vo)-t!r
IQ
(~
RP,R)
1;;!-rIAs\As+1l.
These inequalities are valid for all
82
:5
8:5
8
••
We
add them for
8 =
82,82
+
1,82
+ 2,
...
8.
-
1.
The right hand side can be majorized by a convergent series bounded above by
IQ
(~RP,
R)
I.
Therefore
(8.
-
82)
IAs.l~
:5
-y(vo)-t!r
\Q
(~
RP,R)
\~.
To prove the lemma we divide by
(8.
-
82)
and take
8.
so large that
-y
----.:..--E.::.!~I
:5
v •.
v~
(8.
-
82)
p
Remark
8.2.
If
v.
is independent
of
wand
R,
also
8.
and hence A are independent
of
these quantities.
Remark
8.3. The process desCribed in Lemma 8.1 has a double scope. Given v.,
it determines a level
p.
+ -
2":'
and a cylinder so that the measure
of
the set where
u is above such a level can be made smaller than
v.,
on that particular cylinder.
9.
The second alternative concluded
Next we show that indeed u is strictly below its supremum
p.+
in a smaller box
coaxial with
Q
(~RP,
R)
and with the same vertex. To simplify the symbolism
~~~
2
a.
= !a
o
= !
(~)P-
,
2 2 w
and write accordingly Q
(~RP,
R)
=Q
(a.flP,
R).

9. The second alternative concluded
65
LEMMA 9.1.
The
number
II.
(and hence
s.
and A)
can
be
chosen so that
u(x,
t)
:5
JI.+
-
2S~+l
'
PROOF:
We
will apply the local energy estimates
of
Proposition 3.1
of
Chap. II
over the boxes
Q
(a.R~,
R.n.)
to the function (u - k
n
)+, where for all n =
0,1,2,
...
,
and
The cutoff functions
(n
are
taken to satisfy
0<
(n(X, t), Vex, t) E Q
(a*R~,
R.n.)
, and
(n
==
1 in Q
(a.R~+l'
R.n.+l);
(n = 0 on the parabolic boundary
of
Q
(a.~,
R.n.),
I
DI' I <
271+1
0 < a
I'
< 2
P
(n+1)
,>n -
R'
-
8:r,>n
-
a.RP
,
..!..
= 2
(!:!L)P-2
A = 2
S
••
a.
A '
With these choices, inequalities (3.8)
of
Chap. II take the form
(9.1)
esssup
I(u
- k
n
)!
(~(x,
t)dx
+ f f
ID
(u - k
n
)+
(nlPdxdr
-a.R!:<t<O
11
- -
KR..
Q(a.R::,Rn)
2
np
f f 2
np
f f
:5
'Y
Rp
11
(u-kn)~dxdr+
:.RP
11
(u-kn)!dxdr
Q(a.R::,Rn)
Q(a.R!:,Rn)
p(1+")
+~
L~At.."(T)lidT}
·
First by the definition
of
a.
I(U
- k
n
)!
(~(x,
t) dx
~
(2~.)
2-p
I (u -
kn)~
(~(x,
t) dx
KR..
KR
..
~
2a.1I
(u
- k
n
)+
(nll:,KR
..
(t).
Next, using again the definition
of
a., the first two terms on the right hand side
of
(9.1) are estimated above by
