DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.

46
ill.
HOlder
continuity of solutions
of
degenerate
parabolic equations
Remark
3.1. The proof of Proposition
3.1
will show that indeed it
is
sufficient
to
work with
the
number w
and
the
cylinder Q
(aoRP,
R)
linked
by
(3.1)
essosc u <
w.
Q(aoRp,R) -
This fact
is
in
general not verifiable, for a given
box,
since its dimensions would
have to
be
intrinsically defined
in
terms
of
the essential oscillation of u within it.
Therefore the role of having introduced the cylinder Q
(RP-E,
2R)
and hav-
ing
assumed (2.2)
is
that (3.1) holds true for
the
constructed
box
Q
(aoRP,
R).
It
will
be
part of the proof of
Pf<)position
3.1
to show that at each step
the
cylinders
Q(n)
and
the
essential oscillation
of
u within
them
satisfy
the
intrinsic geometry
dictated
by (3.1).
To
begin the proof. inside Q (
aoRP
,
R)
consider subcylinders of smaller
size
constructed
as
follows. The number w being fixed. let
So
be
the smallest positive
integer
such that
(3.2)
w
-
<6
2
8
0 _
0,
where the number 6
0
is
introduced
in
(3.11) of
Chap.
II
in
the
derivation of the
local energy estimates. Then construct cylinders
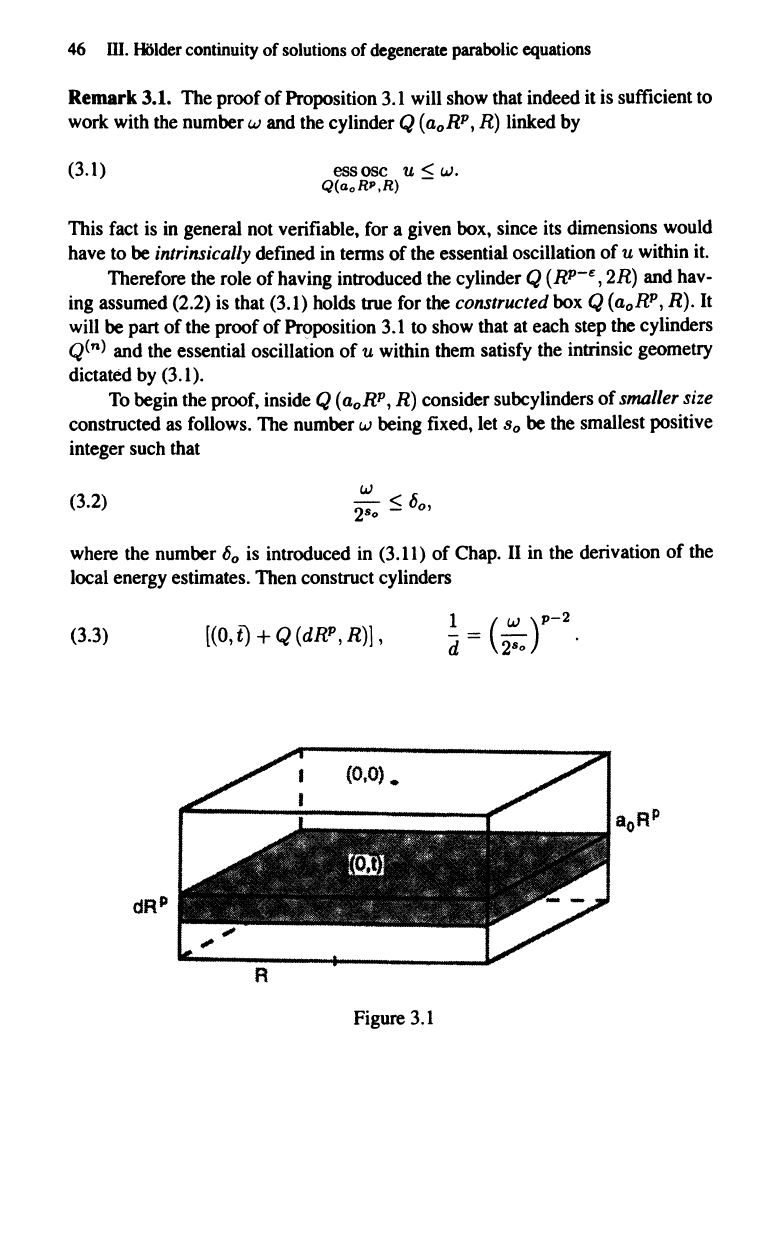
(3.3)
[(0,
t) + Q (dR",
R)]
,
R
Figure
3.1

3.
The main proposition
47
These are contained inside Q
(aoRP,
R) if the number A
is
chosen larger that
2
80
and if t ranges over
_ {AP-2 _ (2
80
}P-2}
RP
< t <
o.
w
p
-
2
The structure of
the
proof
is
based
on
studying separately
two
cases. Either
we
can find a cylinder of the type of
[(0,
l)
+ Q
(dRP,
R)] where u
is
mostly large,
or such a cylinder cannot
be
found.
In either case
the
conclusion
is
that the essential
oscillation of u
in
a smaller cylinder about
(xo,
to)
decreases
in
a
way
that can
be
quantitatively measured.
In
the arguments to follow
we
assume (2.2)
is
in
force
and determine later the numbers
A, e and
eo.
Remark
3.2. For later
use
we
estimate the quantity
(
w )
-2
1!1!±.cl
G(w,
R}
==
'YRNIt
2
8
0
dr,
where
'Y
is
a constant depending only upon the data and
K.
is
defined
in
(3.5) of
Chap. II. From the defu\ition of
din
(3.3) it follows that
(3.4)
and
G(w
R}
< A
RNltw-
b
, _ I ,
where b = 2 +
(p
_
2)
p(1 +
K.}
r
Al
= A
2
+(P-2)P(1;,,)
•
Along the proof
we
will encounter quantities of the type
AiRNltw-b,
i =
1,2,
...
,t, where
Ai
are constants that can
be
determined a priori only
in
terms of
the data and are independent of
w
and
R.
We
may
assume without loss of generality
that they satisfy
(3.5)
Indeed if not,
we
would have
w:5
C
Reo
for the choices
C = max
A~/b
l~i9
t
and
and
the first iterative step of
the
Proposition would
be
trivial.
Remark
3.3. The proof below and (2.2) show that
the
numbers e
and
eo
can
be
taken
as
NK.
eo
=
b'
e =
(p-
2}eo.
In
the estimates to follow
we
denote
with
'Y
a generic positive constant that
can be calculated a priori depending only
upon
the data and that
may
be
different
in
different contexts.

48
ill.
HOlder
continuity of solutions
of
degenerate parabolic equations
3-(i). About the dependence on
lIulloo.n
T
We
will use the energy and logarithmic estimates
of
Propositions 3.1 and 3.2
of
Chap. II for the truncated functions
(u
-
k)±
over cylinders contained in
Q
(aoRP
,
R).
When working with
(u
-
k)
_ we will use the levels
for some
i
~
o.
These levels are admissible since
lI(u
-
k)-lIoo.Q(IJoRP.R)
::;;
6
0
•
When working with
(u
-
k)
+ we will take levels
for some
i
~
o.
These are also admissible since
II
(u - k)+
lloo.Q(lJoRP.R)
::;;
6
0
•
Let us fix 6
0
as
in (3.11)
of
Chap. II. Then, sincew::;;2I1ull
oo
.nT'
(3.2) holds
true
if
we choose So so large that
2
80
=
8~2I1ulloo.nT.
Having chosen
So
this way. (3.2) is verified when working within
any
subdomain
of
D
T
•
The a priori knowledge
of
the norm
lIulloo.n
T
is required through the number
So.
If
the lower order terms b(x, t,
u,
Du)
in (1.1) satisfy
(A~)
of
§5
of
Chap. II,
then. as remarked there. the energy and logarithmic inequalities hold true for the
truncated functions
(u
-
k)±
with
no
restriction
on
the levels k. Thus in such a
case
So
can be taken to be one and no a priori knowledge
of
lIulloo.nT
is needed.
The numbers
A and
Ai
introduced in (3.5) will be chosen to be larger than
2
80
• In the proof below we will choose them
of
the type
and
A
. -
2;0+h,
.- ,
i =
0,1,2,
...
,
where
hi
~
0 will be independent
of
lIulloo.nT.
We
have just remarked that
if
the
lower order terms b(x, t,
u,
Du)
satisfy
(A~)
of§5
of
Chap. II, then
So
can be taken
to be one.
We
conclude that for equations with such a structure, the numbers
Ai
can be determined a priori only in terms
of
the data and independent
of
the norm
lIulloo.nT·

4.
The first alternative
49
4. The first alternative
LEMMA
4.1.
There
exists a
number
Vo
E (0, 1) independent 0/
w,
R, A
such
that
if/or
some
cylinder
of
the
type
[(0,
t) + Q
(dRP, R)]
I(X,t) E
[(O,t)
+Q(dRP,R)] lu(x,t} < IL- +
2~0
1::5
VolQ
(dRP,
R)
I,
then
(4.1)
u(x,t)
>
IL-
+
2S~+1
a.e.
(x,t)
E
[(O,t)
+Q(d(f)",f)]·
PROOF:
Fix
a cylinder for which the assumption of the lemma holds.
Up
to a
translation
we
may
assume that (0, t) = (0,
O),
and
we
may work within cylinders
Q(dPP,p) , O<p::5R. Let
R R
Rn
="2
+
2n+1'
n =
0,1,2,
...
,
construct
the
family of nested cylinders Q
(dR~,
Rn)
and
let
(n
be
a piecewise
smooth cutoff function
in
Q (
dR~,
Rn)
such that
(4.2)
We
will
use
the
energy inequalities
of
Proposition
3.1
of Chap
II.
written over
the
cylinders Q
(d~,
Rn),
for the functions (u - k
n
)-.
where
forn=O,
1,2,
...
,
k = -
~
W
n
IL
+
28
0
+1
+ 2
80
+1+
n
'
In
this setting. (3.8) of Chap.
II
takes the
form
(4.3) esssup
J(u
- k
n
):
(!(x,
t)dx +
jr
flD
(u -
knL
(nlPdxdr
-dR~<t<O
J ,
KRn
Q(dR~,Rn)
::5
7:
{ J J (u -
kn)~
dxdr +
~
J J (u - k
n
):
dXdr}
Q(dR~,Rn)
Q(dR~,Rn)
,,(1+,,)
+7 { J
IAkn'RJr)l~dr}
r
-dR~
We
will
show
that
as
n
-+
00
50
DI.
HOlder
continuity of
solutions
of
degenerate
parabolic
equations
Ilx[(U-k
n
L
>O]dxdr-+O.
Q(dR!:.Rn)
Since k
n
'\.
koo
=
J,L-
+
2.::'+1'
this would imply that
thereby proving the lemma.
We
observe that
and estimate above the first two tenns on the right hand side
of
(4.3) by
7
~:
(2:
0
)2
(2:
0
r-
2
II
X
[(u
- knL >
0]
dxdr
Q(d~.Rn)
+7:
(2:J
2
~
II
X
[(u
- knL >
0]
dxdr
Q(dR~,R,,)
:57:
(2:J"
Ilx[(U-knL
>O]dxdr,
Q(d~.R,,)
where we have used the defmition (3.3)
of
d. Combining these remarks in (4.3)
and dividing through by d, we arrive at
(4.4)
esssup
I(u
-
kn)~
(:(x,
t)
dx
+
-d
1
I
liD
(u - knL
(nl"dxdr
-dR~<t<O
11
KRn
Q(d~.R,,)
:57~:
(2:J"
~
Ilx[(U-knL
>O]dxdr
Q(d~.Rn)
{
0
}~
(
W
),,-2
~
1 I
1:
+7
2Bo
d,.
~dR~IAkn.R,,(r)l·dr
In (4.4) we introduce the change
of
time-variable z =
tid
which transfonns
Q
(d~,
Rn)into
Qn
==
Q(~,Rn)
==
KR"
x{-~,O}.
Setting also
v(·,z) = u(·,zd) and (n(-,z) = (n(·,zd),
the inequality (4.4) can be written more concisely as

4.
The
first alternative
51
where
we
have
set
o
and
IAnl
= J IAn(z)ldz.
-Rl:
Since
(11
-
knL
<n
vanishes
on
the lateral boundary of Qn,
by
Corollary
3.1
of
Chap.
I
we
have
The
left
hand
side
of (4.5)
is
estimated
below
by
II
(11
-
knL
1I:,Qn+l
~
Ik
n
-
k,.+1
IPIAn+1I
~
2P(~+2)
(;:0
r I
A
n+1l·
Combining
these
estimates gives
(4.6)
IA
11+m:;
IAn+d
~
-y4
np
n
RP
~
+~4·P
(2~.r'
dol':"'
1A.lm
tllA.(Z)lidz}
·
Divide
by
IQn+11
and
introduce
the
quantities
Using
also
the
fact
that. by virtue of
Remark
3.2
and
(3.5)
RNIC
(!:!...)
-2
d
P
(1:"! < 1
2
80
- ,
we
obtain
from
(4.6)
in
dimensionless fonn

52
m.
H6lder
continuity of
solutions
of degenerate
parabolic
equations
y.
1 < "'4
np
{y'l+~
+
Y.~Zl+"}
n+
_I
n n n ,
'tin = 0,1,2,
....
Next by the .embedding
of
Proposition 3.3
of
Chap. I
Therefore
Z <
",4
np
{y. +
Zl+"}
n+l
_
Inn
,
'tin =
0,
1,2,
....
From Lemma 4.2
of
Chap. I it follows that Y
n
and Zn tend to zero as n -+
00,
provided
where 8
0
=
min
{
N;"p;
It}.
5. The frrst alternative continued
Suppose the assumptions
of
Lemma
4.1
are verified for some box
of
the
type
[(0,
l)
+ Q
(dRP,
R)].
We
will exploit the fact that at the time level
(
W
)2-
P
(R)P
-8
= t -
2Bo
"2'
the
functionx-+u(x,
-8)
is strictly above the level
",-
+
2.::'+1'
in
the
cube K
R
/
2
•
To simplify the symbolism let us set p =
~
and construct the cylinder
Q(8,p)
==
Kpx(-8,0),
p=
R/2.
The length 8
of
such a cylinder satisfies
(5.1)
- < - < - 2
P
•
(
W
)2-P
8
(W)2-P
2-
0
-
pP
- A
The next lemma asserts that, owing to (4.1), the set where u(·, t) is close to
I.e
,
within the smaller cube
KR/4'
can be made arbitrarily small for all time levels
-8~t~0.

S.
The fllSt alternative continued
S3
LEMMA 5.1.
For
every
number
Vi
E (0,1),
there
exists a positive integer
81.
depending
only
upon
the
data
and
independent
of
w, R,
such
that
'lit E
(-9,0).
PROOF:
Consider the logarithmic estimates
of
Proposition 3.2
of
Chap. II, written
over the cylinder
Q
(0,
p),
for
(u-k)_,
As a number c in the definition
of
W,
we take
w
c -
-=--7":'"":"-
- 2
s
o+
i
+
n
'
where n is
to
be chosen. Thus we
take
where
n>
1,
Hi; = esssup
(u
-
(JL-
+ 2
W+
i
))
::;
2
w+
i
.
Q(fJ.p)
So
_
80.
For
t=
-0,
by virtue
of(4.1)
we have
(u
-
(JL-
+
2.~+dL
=0,
and therefore
W(x,
-0)
= 0,
These remarks in (3.14)
of
Chap. II yield
(5.2) I w
2
(x, t)(P(x)dx
::;
; II
W!W
u
!2-
P
dxdr
Kp Q(fJ.p)
.ell±!!l
+
~(2":'+'
r'
~
+
In
H,
(2<.:,+0>
n
(lIA',p(T)
I i
dT)
· ,
where A;.i·) is defined in (3.4)
of
Chap. II and x
-+
(x)
is a piecewise smooth
cutoff function in
Kp
that equals one on
Kp/2
and such that
ID(I::;
4/
p.
Next
W::;ln(
~
)
=nln2
~
and
! !
2-P
! _ W
!P-2
(W
)P-2
WU
=
Hk
- (u - k)_ + 2
so
+l+
n
::;
2
80
•
Therefore, in also view
of
(5.1), the first term on the right hand side
of
(5.2) is
estimated above by

54
m.
Itilder continuity of
solutions
of
degenerate
parabolic
equations
; ffl[lll[lul2-PdXdT S
'Yn;
(2~JP-2IKp/21
S 'YnAP-2IKp/21,
Q(9,p)
where
l'
and A are constants depending only
upon
the data. and A
has
to
be
deter-
mined
later.
The
second tenn
is
estimated
by
using
the
conditions (3.6). (3.7) of
Chap.
II.
linking the parameters r,
q,
K..
This gives
Ei!±cl
~(2'.:,+or'(l
+ In H;
(2
•.
:'+0
n
(lIA'-"<T)I~
dT)
.
(
w
)-2
(W)-Ei!±cl(P-2)
S'Y
n
2
so
+1+
n
A r R
NIt
IK
p
/
2
1.
The number n
will
be
detennined shortly. depending only
upon
the data and
inde-
pendent of w,
p.
Therefore
by
virtue of Remark 3.2
and
(3.5)
we
may
estimate
(
w
)-2
(~)_P(1:")(P_2)
Nit
<
n 2
Bo
+l+
n
A R _
1.
Combining these remarks
into
(5.2) yields
(5.3)
f 1[12(x,t)dx S
'Y
nAP
-
2
I
Kp/2
I ,
Kp/2
where
we
have used the fact that (== 1 on K
p/2.
The
integral
in
(5.3)
is
estimated
below
by
extending the integration
to
the smaller set
{x
E K
p
/ 2
1
u(x,
t) <
,.,.-
+
2Bo~l+n}
,
t E
(-0,0).
On
such a set
and
since
the
right hand side of this inequality
is
a decreasing function of Hi; •
we
have
1[12
~
In2(
20:+1
) = (n _
1)21n2
2.
2°o+
n
Putting this
into
(5.3) gives that for all t E
(-0,0)
(5.4)
Ix
E K
p
/
2
I
u
(x,
t)
<,.,.-
+
2Bo~l+n
I S
'Y
AP
-
2
(n
~
1)2I
K
p/21·
To
prove
the
lemma
we
have only
to
choose n sufficiently
large.

6. The
fmt
alternative concluded
55
6. The first alternative concluded
The infonnation
in
Lemma
5.1
will
imply that u
is
strictly bounded
away
from
p.-
in
a smaller cylinder.
To
make
this precise. consider the
box
Q(O,~)
=
Kp/2X(-0,0),
where
(J
satisfies
the
bounds
in
(5.1).
P = R/2,
LEMMA 6.1.
The
numbers
V1
E (0,1) and
81
» 1
can
be
chosen
a priori
depen-
dent only
upon
the
data and independent
of
w and R.
so
that
w
u(x, t) >
p.-
+ 2
81
+1'
a.e.
(x, t) E Q
((J,~)
.
PROOF:
We
will
use
the local energy estimates
of
Proposition
3.1
of
Chap.
II
in
the following setting.
Let
n = 0,1,2,
...
,
construct the cylinders
Q
((J,
Pn)
and let x
-+
(n (x)
be
a piecewise smooth cutoff
function
in
KPn
that equals one
on
KPn+1
and such that ID(n
1:$
2
n
+
3
/
p.
Write
the
inequalities (3.8) of
Chap.
II
over Q
(0,
Pn)
for
the
functions (u - k
n
)_.
where
w w
k
n
= p.- + 2
81
+
1
+ 2
s
l+
Hn
'
and observe that. owing
to
the
conclusion of Lemma 4.1.
(u -
knL
(x,
-0)
=
0,
IrIx
E
KPn,
n =
0,1,2,
....
With
these choices. the energy inequalities yield
(6.1) sup
j(u
-
kn)~
'~dx
+
,),-1
r
riD
(u -
knL
(niP
dxdr
-8<t<0
JJ
KPn
Q(8,Pn)
£lli!!.!.
::;
')'~P
jj(u
-
kn)~
dxdr
+"(
{JIAkn,pJr)lidr}
r
Q(8,Pn)
-8
The
first tenn
on
the left hand
side
is
estimated
below.
for
all t E
(-0,0).
by
j(u
-
kn)~
'~dx
~
(2~1)
2-p
j(U
-
kn)~
'~dx
KPn KPn
> 2-P
(2
81
)P-2
~
j(u
-k
)P
I"Pdx
>
~
j(u
-k
)P
I"Pdx
- A
pP
n -
'>n
-
pP
n -
'>n
,
KPn
KPn
