DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.

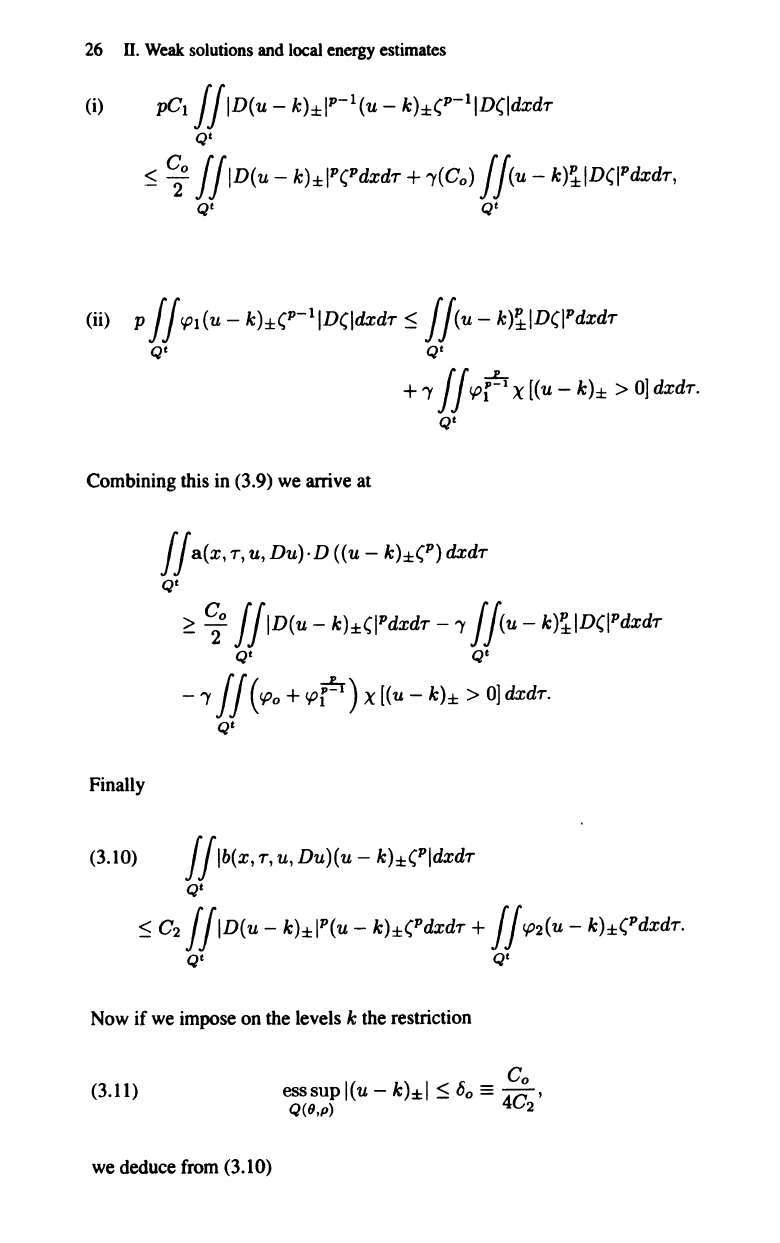
26 ll.
Weak
solutions and local energy estimates
(i)
pC
I
IIID(U
- k)±IP-I(U - k)±(P-IID(ldxdr
Q'
~
~o
IIID(U
- k)±IP(Pdxdr +
'Y(C
o
)
II(u
-
k)~ID(IPdxdr,
Q' Q'
(ii) p
II
CPI(U
- k)±(,,-IID(ldxdr
~
II(u
-
k)~ID(IPdxdr
Q' Q'
+'Y
IlcprX[(U-k)±
>Ojdxdr.
Q'
Combining
this
in (3.9)
we
arrive
at
Finally
II
a(x, r, u,
Du)·D
«u
- k)±(P) dxdr
Q'
~
~o
IIID(U
- k)±(IPdxdr -
'Y
II(u
-
k)~ID(IPdxdr
Q' Q'
-'Y
II(CPo+cp(=r)X[(u-k)±
>Ojdxdr.
Q'
(3.10) f
Ilb(X,
r, u, Du)(u - k)±(Pldxdr
Q'
~
C
2
fllD(u
- k)±IP(u - k)±(Pdxdr +
II
CP2(U
- k)±(Pdxdr.
Q' Q'
Now
if
we
impose on the levels k the restriction
(3.11)
we
deduce
from
(3.10)
(
Co
esssupi
u -
k)±1
~
6
0
==
4C
'
Q(fJ,p) 2

3.
Local integral inequalities
27
(3.10') f
flb(x,
r, u, Du)(u - k)±(PI dxdr
Qt
:5
~o
fflD(u
- k)±IP(Pdxdr +
II
C{)2(U
- k)±(Pdxdr
Qt Qt
:5
~o
!!ID(U
- k)±(IPdxdr +
Do
!!
C{)2X
[(u
- k)± >
0]
dxdr
Qt Qt
+')'
f
I(u
-
k)~ID(IPdxdr.
Qt
Combining these estimates and recalling that t E (
-6,
0) is arbitrary, we obtain
sup
f(u
- k);(P(x, t) dx + C
2
°
jr
flD(u - k)±(IPdxdr
-9<t<O
J
Kp
Q(9,p)
:5
I (u - k);(P(x,
-6)dx
Kp
+
')'
f
I(u
-
k)~ID(IPdxdr
+
')'
If(u
-
k);(p-l(t
dxdr
Q(9,p)
Q(9,p)
+')' fl(C{)o + C{)r
+C{)2)x[(u-k)±
>Ojdxdr.
Q(9,p)
By HOlder's inequality
11(C{)o+C{)r
+C{)2)x[(u-k)±
>Ojdxdr
Q(9,p)
1'-1
:5
II".
+ "r +
'1'211.,.,,,,
{}
A~p
(T
>I'"
'"
dT
}
..
Therefore recalling the definition (3.5)
of
the numbers
q,
r,
It,
inequality (3.8) fol-
lows.
Remark
3.2. The proof shows that the number
Do
in (3.11) has
to
be chosen small
according to the constant
C
2
•
If
in (1.1) b(x, t,
u,
Du)
=0,
then
Do
can be taken to
be
infinite and no restriction is imposed on the levels
k.
Remark
3.3.
If
the lower order terms
C{)i
are all zero, then in (3.8) the last term can
be
discarded.

28
II.
Weak
solutions and local energy estimates
3-(ii). Local logarithmic estimates
Introduce
the
logarithmic function
(3.12)
1/1
(Hr,
(u - k)±,c)
==
In+ {±
Hr
},
0 < c <
Hr,
Hie
- (u - k)± + c
where
Hr
is
defined
in
(3.3) via the levels k,
and
for s > 0
In+ s
==
max{lns;
OJ.
In
the cylinder
[(
x
o
,
to)
+ Q
«(J,
p)
I
we
take a cutoff function satisfying (3.1) and
(3.13)
(
is
independent
of
t E
(to
-
(J,
tol.
PROPOSITION
3.2.
Let u
be
a locally bounded
weak
solution
of
(1.1)
in
th.
There
exist constants
"(
and 6
0
that
can
be
determined a priori only
in
terms
of
the
data.
such
that for every cylinder
(Xo,
to)
+
Q«(J,p)
E
{h
andforevery level k
satisfying
(3
J)
for 6 S 6
0
(3.14) sup !
1/1
2
(Hr,
(u - k)±,
c)
(x, tKP(x) dx
to-9<t<to
[zo+K,,]
< f
1/1
2
(Hr,(u-k)±,c)
(x,to-(JKP(x)dx
[zo+K,,]
+
'Y
!!
1/111/11£
(Hr,
(u - k)±,
c)
1
2
-
P
IV(I
P
dxdr
[(zo,t
o
)+Q(9,p)]
~
+;
(1
+In
~t)
ll.IAUT)li
dT
} ·
PROOF:
As
before,
we
may
take (x
o
, to)
==
(0,
0)
and
will
work
within the cylin-
der
Qt introduced earlier.
Also,
to simplify the symbolism let
us
set
(3.15)
In
(1.5) take
the
testing function
I{) =
~h
[1/I2(Uh)]
(P
=
[1/1
2
(Uh)]'
(P.
By
direct calculation
[1/I2(Uh)]"
= 2(1 +
1/1)1/112
E Lioc(lh)
which implies that such a
I{)
is
an
admissible testing function
in
(1.5). Since
1/1
(
Uh)
vanishes
on
the
set where
(Uh
- k)±=O,

3.
Local integral inequalities
29
II !
1£h
[1/12]'
(Pdxdr =
II!
1/1
2
(Pdxdr
Qt Qt
= I
1/I2(1£h)(Pdx
- 1
1/I2
(1£h)(PdX.
Kpx{t}
Kpx{-9}
Therefore letting h
-+
0
II !
1£h
[1/12]'
(Pdxdr ----+ I
1/1
2
(Ht,
(1£
-
k)±,c)
(Pdx
Qt
Kpx{t}
-I
1/1
2
(Ht,
(1£
-
k)±,
c)
(Pdx.
Kpx{
-9}
To estimate the remaining tenns we let h
-+
0 first and then make use
of
the
structure conditions
(Al)-(As).
/ / a(x,r,1£, D1£)·D",dxdr
~
2C
o
11(1
+
1/1)
1/I,2ID1£I
P
(Pdxdr
Qt
Qt
- 2
11(1
+
1/1)
1/1,2"'0
(x, r)(Pdxdr
Qt
- 2pCl /IID1£
IP
-
1
1/l1/l'(P-
1
ID(ldxdr
Qt
- 2pCl II
1/11/1''''1
(x, r)(P-1ID(ldxdr.
Qt
From this, by repeated application
of
Young's inequality
1/
a(x,r,1£,D1£)·D",dxdr
~
Co
11(1
+
1/1)
1/1'2
I
D1£IP(Pdxdr
Qt
Qt
For the lower order tenns we have
-
2//(1
+
1/1)
1/1,2"'0
(x, r)(Pdxdr
Qt
-
-y(P)
111/1
(1/I,)2-
p
ID(IPdxdr
Qt
-
-y(P)
//1/1
(1/1,)2
",r
(Pdxdr.
Qt

30
n.
Weak
solutions
and
local
energy
estimates
/ /lb(X,
T,
U,
DU)1/J'I/l(PldxdT
:5
C2
//IDuIP
(1
+
1/J)
,t/P1/J,-l(Pdxdr
Qt
Qt
+
//
'P21/J1/J'(Pdxdr.
Qt
Next we observe that by virtue
of
(3.3) and the definition (3.12) and (3.15)
of
1/J
1/J'-1
=
Ht
-
(u
- k)± + c <
26
and
Therefore by virtue
of
the choice (3.11)
of
the levels k we have
/
/lb(x,T,
U,
Du)1/J1/J'(PldxdT
:5
~o
//IDU
IP
(1
+
1/J)
1/J12(PdxdT
Qt
Qt
+
~
In
(
~t)
//1'P2IX
[(u - k)± >
OJ
dxdr.
Qt
Collecting these estimates we arrive at
/
!lI
2
(Ht, (u - k)±, c) (Pdx
Kpx{t}
:5
/!lI
2
(Ht, (u - k)±,c) (Pdx +
"Y
//1/JI1/J'1
2
-
P
ID(I
P
dxdT
Kpx{
-9}
Q(9,p)
+;
(1+1n~t)
//('Po
+
'Pr
+'P2)X[(u-k)±>OJdxdT
Q(9,p)
where we have used the fact that c <
1.
Treating the last integral as before proves
the Proposition.
Remark
3.4.
If
the constant
C2
in (A3) is zero, then we may take 6 =
00
and there
is no restriction on the levels
k.
Also
if
'Pi
=0,
i=O,
1,2,
then the last term
on
the
right hand side
of
(3.14) can be discarded.
Remark
3.5. In any case, whence the constant 6
0
has been chosen according to
(3.11). the constant
"Y
on
the right hand side
of
either (3.8)
or
(3.14), is independent
o/u.lt
is only the levels k that might depend upon the solution u via (3.11).

4.
Energy
estimates
near
the
boundary
31
4.
Energy
estimates near
the
boundary
We
assume u
is
a weak solution
of
either the Dirichlet problem (2.1) or
the
Neu-
mann
problem (2.7), satisfying
in
addition
(4.1) uEV>C'J({h)
and
UEL
2
(0,T;W
1
,PUh»).
The assumptions (D),
(U
0), (N),
(N
-
(i»
on the boundary data will
be
retained.
We
will derive energy
and
logarithmic estimates, similar to those of Propositions
3.1
and
3.2, near the lateral boundary ST
as
well
as
at
t =
O.
Fix a point (xo,
to)
on
ST,
and
construct the
box
[(xo,
to)
+ Q
(8,
p)],
where
8
is
so small that
to
-
8>0.
In
[(xo,
to)
+ Q (8,
p)]
introduce a piecewise smooth
cutoff function
(x, t) -
«x,
t) satisfying (3.1).
We
observe that
for
all
t E (t
o
-
8,
to),
x-«x,
t) vanishes on the boundary of[xo +
Kp]
and
not
on
the
boundary
of
[x
o
+
Kp]
n
n.
Here
the interior quantities introduced
in
the previous section
are
modified
as
follows
esssup I(u -
k)±1
==
D~
$
6,
[(xo,t
o
)+Q(9,p)]nn
T
(4.2)
where 6 $ 6
0
and
6
0
is
a parameter chosen according
to
(3.11). Analogously
we
define the logarithmic function
(4.3)
!Ii(D~,(U-k)±,C)==ln+{
±
D~)
},C<D~'
Dk
- (u - k ± + C
and introduce
the
sets
(4.4)
B~p(7")
==
{x
E
[xo
+
Kp]
n
nl
(u(x,
7")
- k)± >
O}.
4-(i). Variational boundary data
Let
U
be
a
weak
solution
of
(2.7) satisfying (4.1) and assume in addition that
(4.5)
an
is
of class
Cl+~
for some A E (0, 1).
PROPOSITION
4.1.
There
exist constants
"(
and 6
0
that
can
be
determined
a
pri-
ori only
in
terms
of
the
data
and
the
quantities
lIulloo,nT
and
IIlanllll+~'
such
that
for
every
(xo,
to)
E ST./or
every
cylinder
[(xo,
to)
+ Q
(8,
p)]
such
that
to-O>O
andfor
every
level k satisfying (4.2) for 6 $ min{ 6
0
;
1}
(4.6) sup
j(u
-
k)~(P(x,
t) dx +
,,(-1
jr
f ID(u - k)±(I
P
dxd7"
to-9<t<to
J
[xo+Kp]nn
[(x
o
,t
o
)+Q(9,p)]nnT
$ f (u - k)'i(p(x,
to
- 8) dx +
"(
f f (u -
k)~ID(IPdxd7"
[xo+Kp]nn
[(xo,t
o
)+Q(9,p)]nn
T
1!.ll±.cl
+"(
jj(U-k)~(P-l(tdxd7"+"({lIB~p(7")lidT}
r
[(x
o
,t
o
)+Q(9,p)]nnT
0-
9

32 II. Weak solutions and local energy estimates
Moreover
if (
is
independent
oft
e
(to
-
fJ,
to),
(4.7) sup
J!li
2
(D~,
(u - k)±, c) (x, t)(P(x) dx
to-9<t<to
[zo+Kp)nn
~
J!li
2
(D~,
(u - k)±,
c)
(x,
to
-
fJ)(P(x)
dx
[zo+Kp)nn
+
')'
J J
!lil!li
u
(D~,
(u - k)±,c) 1
2
-
P
ID(I
P
dxdT
[(Zo,t
o
)+Q(9,p»)nnT
~
+ ;
(I
+In
D!)
Ll.IB~p(T>I:dT}
·
where
the
numbers
q,
r,
It
satisfy (3.6)-(3.7).
Remark 4.1.
If
the
Neumann
data
are
homogeneous, i.e.,
.,pi
= 0, i =
0,
1,
and
'Pi
=0,
i=O,
1,2, and b(x,
t,u,Du)
=0.
then
we
may
take
6=00
and
the
levels
k
are
not
restricted.
Remark 4.2. The proof below
is
local
in
nature
and
it
shows
that (4.6)-(4.7) hold
true for weak solutions that satisfy the
Neumann
data on a portion of ST. Accord-
ingly,
only such a portion
is
required
to
be of class
CHA.
Also.
no
reference
to
initial data
is
necessary.
PROOF
OF
PROPOSITION
4.1:
Fix
(xo,
to)
e ST,
assume
that (xo,
to)
coincides
.
with
the origin and
work
with
cubes Kp and cylinders Q(fJ,p). Since
an
is
of
class
CHA,
for sufficently small
p,
the portion of
an
within
the
cube K
p.
can be
represented
in
a local system of coordinates
as
a portion
of
the hyperplane x N = 0
and
KpnnC
{XN
>O}. Set
(4.8)
K:
=
Kpn{XN
>
O}
and
Q+
(fJ,
p)
= Q
(fJ,
p)n{XN >
O}.
Without loss of generality
we
may
assume that
(2.11)
is
written
in
such a coordinate
system.
To
derive (4.6),
in
(2.11)
we
take
the
testing functions
and let
h
-+
O.
All
the terms
in
(2.11)
are
treated
as
in
the proof
of
Proposition 3.1,
except
for
the
boundary integral.
We
arrive
at
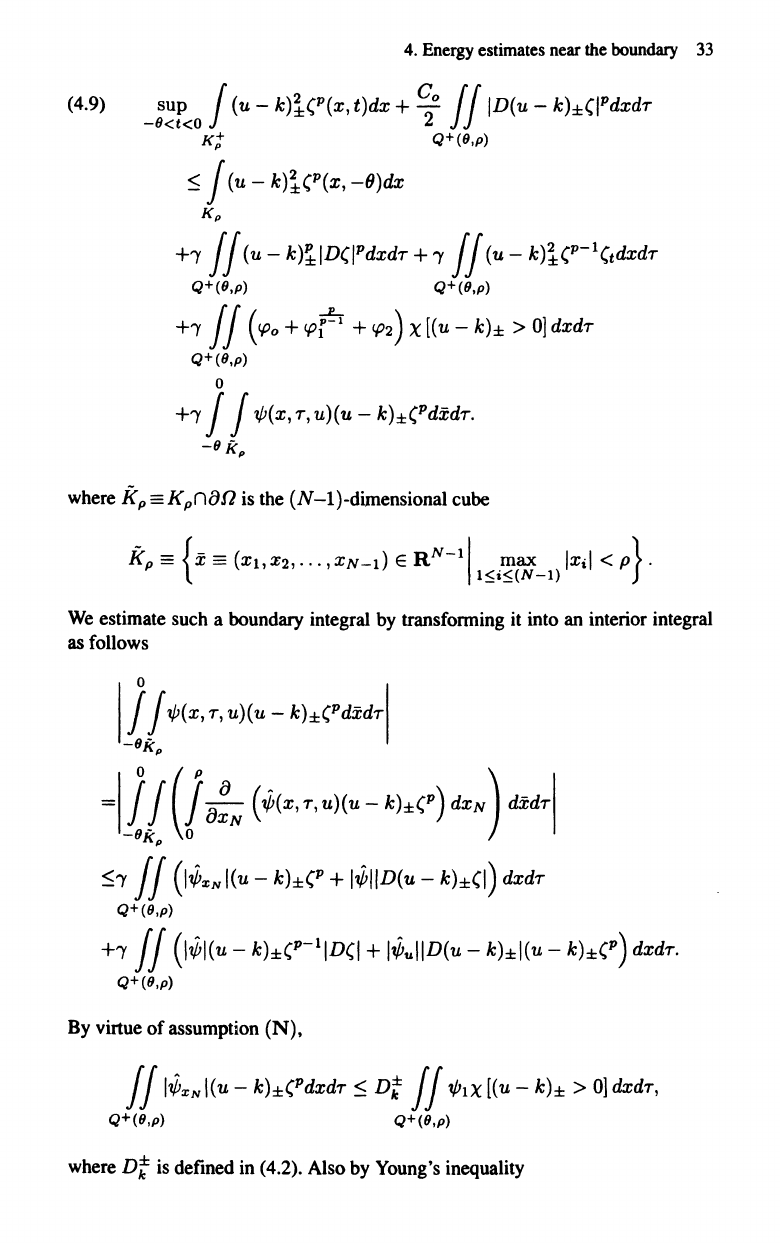
4.
Energy
estimates
near
the
boundary
33
(4.9)
sup
I
(u
-
k)~(P(x,
t)dx
+ C
2
°
jr
f
ID(u
- k)±(IPdxdT
-8<t<O
J
K:
Q+(8,p)
~
I
(U
-
k)~(P(x,
-9)dx
Kp
+1' II (u -
k)~ID(IPdxdT
+
l'
II (u -
k)~(p-l(tdXdT
Q+(8,p)
Q+(8.p)
+1'
II
(<,00
+
<,Or
+
<,02)
X
[(U
-
k)±
>
OJ
dxdT
Q+(8.p)
o
+1'
I I ¢(X,
T,
U)(U
- k)±(PdxdT.
-8
Kp
where
Kp
=Kpnan is the
(N-l)-dimensional
cube
We
estimate such a boundary integral by transforming it into an interior integral
as follows
I J I .,(x,
T,
u)(u - k)±C"dXdTI
-8K
p
~
11
(/
a:N
(,i(x,
T,
u)(u -
k)±(p)
dx
N
)
dXdT
p
~1'
I I
(I~ZN
I(u -
k)±(P
+
1~IID(u
-
k)±(I)
dxdT
Q+(8,p)
+1'
II
(1,z,I(u
- k)±(P-1ID(1 +
l~ullD(u
- k)±I(u -
k)±(p)
dxdT.
Q+(9,p)
By virtue
of
assumption
(N),
II
I~ZNI(u-
k)±(PdxdT
~
Dt
II
¢lX[(u-k)±
> OjdxdT,
Q+(9,p) Q+(9.p)
where
Dt
is defined in (4.2). Also by Young's inequality

34
n.
Weak
solutions
and
local
energy
estimates
II
l,pl
{ID(u - k)±(1 + (u - k)±(P-1ID(I} dxdr
Q+(9.p)
~
~o
fl
ID(u
- k)±(IPdxdr +
"((P)
If
(u - k)'±ID(IPdxdr
Q+(9.p)
Q+(9.p)
+
"(
(p,
\lu\lao.aT)
II
(?/Io
+
?/Ilr;;~
X
[(u
- k)± >
0]
dxdr.
Q+(9.p)
Finally
f f
l,puIlD(u
- k)±I(u - k)±(Pdxdr
Q+(9.p)
~
"(
II
l,pul
{ID(u - k)±(I(u -
k)±(p-l
+
(u
-
k)~(P-IID(I}
dxdr
Q+(9.p)
~
~o
II
ID(u-k)±(I
P
dxdr+"(p,6
0
)
fl(u-k)'±ID(IPdxdr
Q+(9.p) Q+(9.p)
+
"(
(p,
"u\lao.a
T
)
If
?/1ft
X
[(u
- k)± >
0]
dxdr.
Q+(9.p)
Combining these estimates implies that the boundary integral on the right hand
side
of
(4.9) can be estimated by
~o
fIID(U
- k)±(IPdxdr +
"((P,
"u"ao.a
T
)
ff
(u - k)'±ID(IPdxdr
Q+(9.p)
Q+(9.p)
+ "(p,6
0
)
ff
(1
+?/Io
+
?/Id~
X
[(u
- k)± >
0]
dxdr.
Q+(9.p)
We
put this in (4.9) and, to conclude the proof, estimate the integral involving the
functions
!Pi,
i=O,
1,2,
and
?/Ii,
i=O, I,
as in the proof
of
Proposition 3.1.
The proof
of
the logarithmic estimate (4.7) near the lateral boundary
ST
is
similar to the proof
of
the interior logarithmic estimate (3.14), modulo the modi-
fications indicated above and we omit the details.
4-(;;). Dirichlet boundary data
Let u be a weak solution
of
the Dirichlet problem (2.1), which in addition satisfies
(4.1). The assumption (D) on the boundary datum 9 is retained.
Fix
(xo,to) EST and consider the cylinder [(xo,t
o
) + Q(8,p)], where 8 is
so small that
to
- 8 >
O.
Local energy estimates for u near (x
o
,
to)
are obtained by
taking, in the weak formulation (2.5), the testing functions

4.
Energy
estimates near the boundary
35
integrating over
[(xo,
to) + Q
(8,
p))
and letting h
-+
O.
Such a choice of testing
functions
is
admissible if for
a.e.
t E (
to
-
8,
to),
(4.10) (u(·, t) - k)± (P(x, t) E
W~'P
([xo
+
Kp)
n
0).
Since
x-+((x,
t) vanishes on the boundary
of
[x
o
+
Kp)
and not on
the
boundary
of
[x
o
+
Kp)
n
0,
condition (4.10) will be verified iffor
a.e.
tE
(to
-8,
to)
(u
- k)± = 0
in the
sense of
the
traces on a
[xo
+
Kp)
n
O.
In
view
of
Lemma
3.1
of
Chap.
I, this can be realised for the function (u -
k)+
if
k
is
chosen
to
satisfy
(4.11)
k
~
sup
g.
[(zo
,to
)+Q(
lI,p
»)nST
Analogously
the
functions -(Uh - k)_(P can be taken
as
testing functions
in
(2.5)
if
(4.12)
With
these choices of k
we
may
repeat calculations
in
all analogous
to
those of
Proposition
3.1
and derive energy inequalities for u near
ST.
Analogous consider-
ations hold for a version
of
the logarithmic estimates along the lines of Proposition
3.2.
We
summarise
PROPOSITION
4.2.
There
exist constants
"(
and 6
0
that
can
be
determined a pri-
ori only
in
terms
of
the
data
and
such
that for every (xo,
to)
E
ST
.for every cylinder
[(x
o
, to)
+ Q (8,
p))
such
that
to-8
> 0 andfor every level k satisfying (4.2)for
6
~
6
0
and
in
addition (4.11)for
the
functions (u -
k)+
and
(4.12)
for (u - k)_ ,
the
following inequalities
hold:
(4.13) sup
I(u
-
k)~(P(x,
t)dx +
,,(-1
Jr
f ID(u - k)±(IPdxdT
to-lI<t<to
J
[zo+Kp)nn
[(zo,to)+Q(II,p»)nnT
~
!(U-k)~(P(x,to-(})dX+"(
!!(u-k)~ID(IPdxdT
[zo+Kp)nn
[(zo,to)+Q(II,p»)nnT
~
+"(
II
(u -
k)~(P-l(tdxdT
+
"(
{J
IBt,p(T)lidT}
r
[(zo,to)+Q(II,p»)nnT
0-6
Moreover
if
the
cutoff function (
is
independent
of
t E
(to
-
8,
to),
