DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


86
IV.
mldcr
continuity
of
solutions
of
singular
parabolic
equations
Consider (3.8)
of
Chap.
n,
written over
the
boxes Qn for (u -
knL
and
with the
choice
of
the cutoff functions
(n
{
0
< (n(X,t):5 1, V(x,t) E Qn,
and
(n:1
in Qn+1i
(n
= 0
on
the parabolic boundary of Qni
I
Dr
I < 2,,+2
(...!L)
~
0 < r <
2(2-p)m2
2,,("+2) •
.. n - R 2
m
l
,-
..
n,t
-
R"
In
this setting, (3.8) takes the fonn
(4.1)
sup
j(u
-
kn)~
(:(x,t)dx
_2(,,-2)m2
R"
<t<O
,,-
-
K"
Since
+ j
jlD
(u -
knL
(niP dxdT
Q"
:5
..,:
(2:
1
f-Pjj(U
-
kn)~
dxdT
Q"
+
..,:
2(2-
p
)m
2
j
j(
U -
kn)~
dxdT
Q"
~
+..,
{ J I A;" ,dl R,.
(T)I
idT}
r
-2(,,-2)"'2
Rt
w
sup
(U
-
knL
:5
-2
m
-
1
"""+-m-2'
Q"
the first
two
tenns
on
the right
hand
side
of
(4.1)
are
estimated above
by
..,:
G:f2(2-p)m2j/X.[(u-knL
>O]dxdT.
Q"
To
estimate
below
the
two
integrals
on
the left
hand
side, introduce the level
- 1
k
n
:
2
(kn
+ k
n
+1)
<
kn.
Then for all t E ( -
2(p-2)m2
~,
0)
j(u
-
kn)~
(:(x,t)dx
~
j(kn
- k
n
)2-P
(u
-
kn)~
(:(x,t)dx
Kn
K"
~
G:)
2-p
2(p-2)(n+3)j
(u
-
kn)~
(:(x,
t)dx.
K"
Also
we
have

4.
Rescaled iterations
87
!!ID(U-
knL(nlPdxdr
~
!flD
(u
-
knL
(nl
Pdxdr
Qn Qn
-
'Y:
(2:)2
2
(2-
p
)m
2
!IX
[(u -
knL
>
0]
dxdr.
Qn
Put these estimates
in
(4.1), divide through
by
(;
)
2-1'
2(p-2)(n+3)
and in the resulting integrals introduce the change of variables
l=z
y=
C:J
p x,
which maps Qn into
Setting also
v(y,z)=u
(d1y,2(p-2)m2t) I
((y,z)=«d
1
y,2(p-2)m2t) ,
and
o
An(z)={y
E
KR
..
lv(y,z) < k
n
},
IAnl=!
IAn(z)ldz,
-R~
we arrive at
II
(v -
knL
(nll~p(Q
..
)
~
'Y:;n
(;r
IAnl
~
+
~
G~.r
A.R'"K
W
-'{!
I A.(z) I
~
dz } •
By (3.7),
AoRNICW-b
o
~
1, and
by
Corollary
3.1
of
Chap.
I,
2-(n+3)p
(.!:!-.)P
IA
I
2
m
n+1
~
(kn
-
kn+t)P
l(y,Z) E
Qn+ll
v(y,z)
<
kn+11
~
II
(v
- k
n
)+
1I:,Qn+l
~
II
(v
- k
n
)+
<nll:,Qn
~
'YIAnl~
II
(v - k
n
)+
<nll~p(Qn)
"
~
G~.r
[
:-
1A.I'+"r,
+
1A.1"r,
U
1A.(z)I'
dz }
"'P"]
.

88
IV.
HOlder
continuity
of
solutions
of
singular parabolic equations
Thus setting
we
have the recursive inequalities
Yn+l
~
-y4
n
"
{y~+m:;
+
y~
Z!+K
} ,
Zn+l
~
-y4
n
"
{Y
n
+ Z!+K}.
It
follows
from
these and Lemma 4.2
of
Chap. I that Y
n
and
Zn
tend
to
zero
as
n
-+
00,
provided
Yo
+
Z~+K
~
(2-y)-(l+K)/6
0
4-"(l+K)/6~
==
v
o
,
where
8
0
= min {
NT,;;
It}.
Remark
4.2.
The
proof shows that the number
Vo
depends
upon
p but it
is
'stable'
asp/2,
i.e.,
as
p
--+
2.
Remark 4.3. The conclusion of Lemma
4.1
continues to hold for cylinders of the
type
(4.2)
E=l
QR
(m,{3)==K
r
x
(-{3R"
, 0) ,
r=~:)
P R,
{3
> 0,
provided
{3
is
independent of w
and
R.
In
such a case
we
take m =
ml
and
Vo
will
depend also
upon
{3.
5. The first alternative
Suppose that there exists a cylinder
of
the type of
[(x,
0) + Q
(RJ',
doR)]
making
up
the partition of Q (R",
CoR)
for
which
(3.4) holds. Then
we
apply
Lemma
4.1
with
ml
= 8
0
and
m2
= 0
to
conclude that
(5.1) u(x, t) ?
J.I.-
+
2S~+l'
'v'(x,
t) E
[(x,O)
+ Q «
i)"
,do",)] .
We
view
the
box
[(x,O)
+
Q«i)"
,doi)]
as
a block inside Q (R", coR).
Let
R(w)
be
the
'radius' introduced
in
(3.3). The location
of
x within the cube K'R.(w)
is
only
known
qualitatively.
We
will
show
that
the
'positivity' of (5.1) 'spreads'
over the
full
cube
KcoR.
for all times
(f)"
~
t
~
o.
In
a precise
way
we
will prove

5.
The
flfSt
alternative 89
PROPOSITION
5.1. Assume(5.1)holdsforsomeXEK'R.(w). There exists positive
numbers
Al
and
11
that can be determined a priori only
in
terms
of
the data and
the number A
in
the definition
of
Q
(RP,
coR),
such that either
(5.2)
or
As a consequence we may rephrase the first alternative in the following fonn.
COROLLARY
5.1.
Assume that (3.4) holds for some cylinder
of
the type
of
[(x,D) + Q
(W,
doR)]
making
up
the partition
ofQ
(RP,
CoR).
There exists pos-
itive numbers
A1
and s that can be determined a priori only
in
terms
of
the data
and the number
A
in
the definition
ofQ
(RP,
CoR),
such that either
or
essosc
U:::;"'1
w,
Q(pP,cop)
v P E (0, RI8),
where
1Jl
==
1 -
T(so+'i).
We
regard x as the centre
of
a large cube
which we may assume is contained in the cube
KR1-
•.
Indeed
if
not, we would
have
16c
o
>
R-
E
,
i.e., w <
16r-;
AREo,
- pc
£0=--·
2-p
We
will be working within the box
[(x,D) + Q ( iY,
8c
o
R)]
and will show that the conclusion
of
Proposition 5.1 holds within the cylinder
[(x,
0) + Q (
f)P,
2c
o
R)] .
This contains Q ( f
)P,
CoR),
regardless
of
the location
of
x in the cube
K'R.(w).
5-(i). The p.d.e. in dimensionless form
Introduce the change
of
variables
x-x
x
--+
2c
o
R'
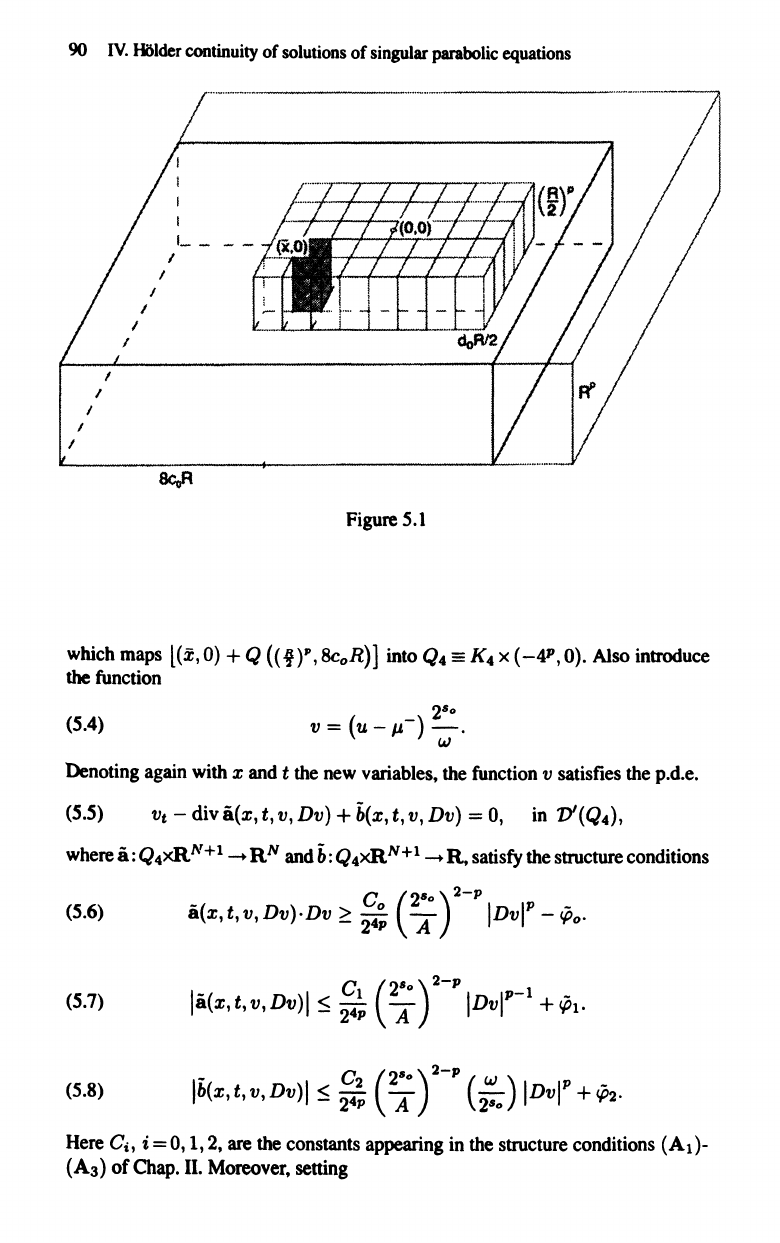
90
IV.
RUder continuity of solutions of singular
parabolic
equations
I
I
I
I
I
I
I
I
I
,-
-
I
I
Figure
5.1
which
maps
l(x,O) + Q
(i)P,8c
o
R)] into
Q4
==
K
4
x (-41',0).
Also
introduce
the
function
(5.4)
Denoting
again
with x
and
t
the
new
variables,
the
function
v satisfies
the
p.d.e.
(5.5)
Vt
- div
i(x,
t, v, Dv) + b(x, t, v, Dv) =
0,
in
1Y(Q4),
where
i:
Q4xRN
+1
-+
aN
and
b:
Q4xR
N
+1
-+
a,
satisfy
the
structure conditions
(5.6)
i(x,t,v,
Dv)·Dv
2:
~;
(2;y-P
IDvlP
-!Po'
(5.8) Ib(x,t,v,Dv)1
~
~~
(~y-P
(2~J
IDvlP
+!P2.
Here
Ci, i
=0,1,2,
are
the
constants appearing
in
the
structure conditions (Al)-
(A3) of
Chap.
II.
Moreover,
setting
s.
The
flJ'St
alternative
91
(5.9)
- -
-~
-
9 =
CPo
+
CPl
+
CP2,
the
function
9 satisfies
(5.10)
where
'"Y
= '"Y(N,p,A,8
0
,data)
is
a constant depending only
upon
the
indicated
quantities
and
b
o
is
defined
in
(3.6). The numbers"
and
q
and
q,
f satisfy (3.5)-(3.7)
of
Chap.
ll.
The
infonnation (5.1) translates into
(5.11) v(x, t) > i
a.e.
(x, t) E
Q(h
o
)
==
{Ixl
< h
o
}
x {-41' < t
:s;
O},
where
(5.12)
doR 1
(28
0
)¥
ho
=
8coR
= 8 A <
1.
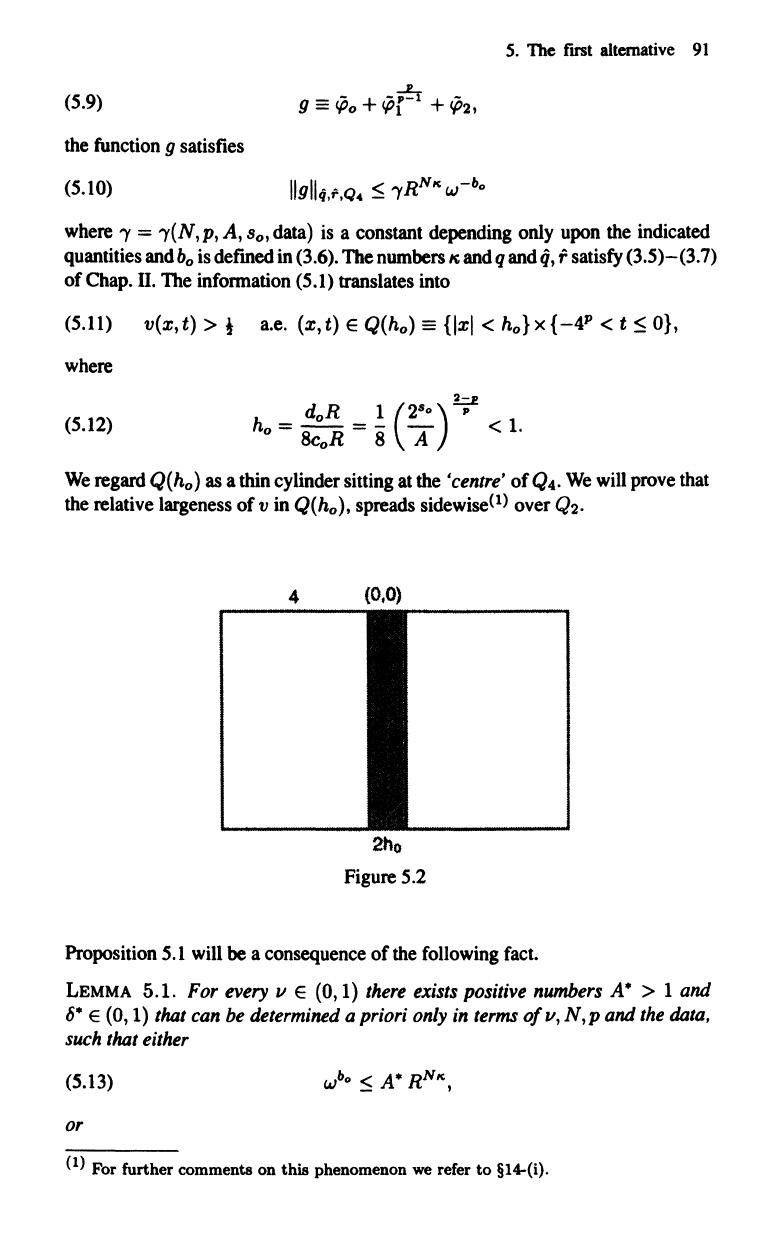
We
regard Q( h
o
)
as
a thin cylinder sitting at
the
• centre' of Q
4.
We
will
prove
that
the
relative
largeness
of v
in
Q(h
o
).
spreads sidewise(l) over
Q2.
4 (0,0)
-------,
2ho
Figure 5.2
Proposition 5.1
will
be
a consequence of
the
following
fact.
LEMMA
5.1. For every
II
E (0,1)
there
exists positive numbers A* > 1 and
6*
E (0,1) that
can
be determined a priori only
in
terms
0/11,
N,p
and
the
data,
such
that either
(5.13)
or
(1)
For further comments on this phenomenon we refer
to
§l4-{i).

92
IV.
H6lder continuity
of
solutions
of
singular parabolic equations
(5.14)
for all time levels
t E
[-2
P
,
0].
Remark
5.1.
The
key
feature of the lemma
is
that
the
set where v
is
small can
be
made
arbitrarily small
for
every time level
in
[-
2
P
,
0].
5-0i). Proof
of
Proposition
5.1
assuming
Lemma
5.1
In Lemma
5.1
we
choose
II
= "
o
where "
o
is
the
number claimed
by
Lemma 4.1,
and determine
6·
=6.(11
0
)
accordingly.
We
let
m2
be
dermed
by
2-
m2
=
6.(11
0
)
and
apply
Lemma
4.1
with
w =
1,
J1.
- =
0,
R =
2,
over the boxes
(0,
t) +
K2
X {
_2
m2
(p-2)2
P
,
O}
=
(0,
t) +
Q2(O,
m2)
as
long
as
they
are contained
in
Q2, i.e., for t satisfying
(5.15)
Since (5.14) holds true for all time levels
-2
P
5 t
50,
each such
box
satisfies
meas{(x,t) E
[(O,t)
+ Q2(0,m2)]I
v(x,t)5
2
-
m2
}5
11
01'MO,m2)1·
Therefore
by
Lemma 4.1 either (5.2) holds or
v(x, t)
;;::
T(m
2
+1)
V(x, t) E Ql.
Returning
to
the
original coordinates
and
redefining
the
various constants accord-
ingly proves Proposition
5.1.
6.
Proof of Lemma 5.1. Integral inequalities
First
we
prove
the lemma under
the
additional assumptions
(6.1)
These will simplify some of
the
calculations and will
be
removed
later.
The
weak
formulation of (5.5) is
(6.2) J Vt'p(x,
t)dx
+ J
sex,
t,
v,
Dv)·Dcpdx
= - J b(x, t,
v,
Dv)cpdx
K4 K4 K4
for
all
-4
P
< t < 0 and all testing functions
cp
E C(Q4)nC
(-4
P
,0; W:,P(K4».

6.
Proof of
Lemma
5.1.
Integral inequalities
93
Let
t
(6.3)
G(t)
==
(6k)-(1+.p)
! IIg(r)
11:14
dr,
-4P
where k and
fJ
are positive parameters to be chosen later, 9 is defined in (5.9)
and q is the number entering in the structure conditions (5.10).
We
define the new
unknow function
(6.4)
w
==
v + G(t),
and rewrite (6.2) in tenns
of
w. Next, by the parabolic structure(l)
of
(6.2), the
truncation
(k -
w)+
is a subsolution
of
(6.2), i.e., for all testing functions
r.p
~
0
(6.5)
!!
(k -
w)+
r.p(x,
t)dx + ! a (x, t,
v,
D (k -
w)+)
·Dr.pdx
K4 K4
~
-!
b (x, t,
v,
D (k -
w)+)
r.pdx
-
G'(t)!
r.p(x,
t)dx.
K4 K4
In
this fonnulation we take the testing function
where,
==
'1
(X)(2
(t)
is a piecewise smooth cutoff function in Q
4,
satisfying
(6.6)
{
0
~
(
~
1 in
Q4,
and (
==
1 in Q2;
( = 0 on the parabolic boundary
of
Q4;
ID(11
~
1,
0
~
(2,t
~
1;
the sets
{x
E
K4
I
(1
(x) >
k}
are convex
Vk
E (0,1).
We
use the structure conditions (5.6)-(5.8), with the symbolism
_.
= Ci
(280
)2-"
C. -
24"
A .
Set also
(k-w)+
(6.7)
~
(w)
_!
ds
k -
[k
_ s +
15k]"
l'
o
(6.8)
[
k(1
+
fJ)
]
!lik(w) =
In
k(l
+
6)
-
(k
-
w)+
.
(1) See §l-(i)
of
Chap.
II.

94
IV.
Hl)lder
continuity of solutions of singular
parabolic
equations
Then we obtain
! j
~1c(w)(1'dx
+
Co
jIDtP
1c
(W)jP(1'dx
K4 K4
~
C
1
j
(IDtP
1c
(w)I()1'-l ID(ldx
K4
+ C
2
2
2
(1'+1)
(2~J
jIDtP
1c
(WW(1'dx
K4
+p
j(~1c(W»(P-I(tdx
K4
By the choice (3.8)
of
the number 8
0
,
the second term involving
IDtP1c(WW
is absorbed in the analogous term
of
the left hand side. The integral involving
IDtP1c(WW-1
is treated by means
of
Young's inequality and the resulting term
involving
1D!P1c(W)\P
is absorbed in the analogous term
on
the left hand side.
The remaining term is majorised by an absolute constant depending only upon
C
i
,
i =
0,
1.
Next,
if
we stipulate to take k in the interval (0,
1J,
the integral in-
volving
(t
is majorised by 'Y/(2 - p), where
'Y
is an absolute constant depending
only
upOn
p. Finally the sum
of
the last two integrals can
be
majorised by an ab-
solute constant. Indeed
We
conclude that there exist constants
.:yo
and
.:y
depending only upon N,
p,
A, 8
0
and the data, such that

7.
An
auxiliary
proposition
95
(6.9)
!J~II:(W)(Pdx+;Yo
JIDI/III:(w)IP(Pdx~
2~P·
K4 K4
Next,
since k E (0,
i)
the
function
I/III:(w)
vanishes
for
alllxl
:5
h
o
•
This
follows
from
the
definition (6.4) of
wand
(5.11). Therefore
we
may
apply
the
Poincare
inequality
(2.9)
of Proposition
2.1
of
Chap.
I,
to
minorise
the
second tenn
on
the
left hand
side
of (6.9).
We
summarise:
LEMMA
6.1.
There
exists
two
constants
'Yo
and
'Y
that
can
be
determined
a priori
only
in
terms
of
N,p, A,
SO
such
that
(6.10) ! J
~k(w)(Pdx
+
'Yo
J I/I:(w) (Pdx
:5
'Y,
K4
K.
where
~k(W)
and
I/Ik(W)
are
defined
in
(6.7)-(6.8).
Remark
6.1.
The
function G(·) introduced
in
(6.3)
is
defined through
the
numbers
k
and
6
which
are
still to
be
chosen.
By
virtue
of
the
structure conditions (5.10),
we
have
G(t):5
'Y(6k)-(1+r-r)
IIgll:;Q4
~
'Y
(6
k)-(l+r-r)
[R
NIC
w-
bo
]
o!r
.
If
we
choose
k6
=
6*
E
(0,
1) depending only
upon
the
data,
we
may
assume
without
loss
of generality that
(6.11)
G(t)
:5
'Y
(6k)-(1+r-r) [R
NIC
w-
bo
]
r-r
:5
6*2.
Indeed,
otherwise
for
such
a selection of
6*
for
some
positive number
(J
depending
only
upon
q
and
p
and
some
'Y
depending
only
upon
the
data.
The
number
6*
will
be
chosen
Shortly
only
in
tenns of
the
data.
In
view
of
(6.11)
we
may
regard
the
function
W introduced
in
(6.4)
as
independent
of k
and
6.
7.
An auxiliary proposition
Introduce
the
quantities
(7.1)
Y
n
==
sup f (P (x, t)
dx,
-4P<t<O
K4n[W(
·,t)<6")
n=0,1,2,
....
The
proof of
Lemma
5.1
is
a consequence of
the
following:
