DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


96
IV.
H6lder continuity
of
solutions
of
singular parabolic equations
PROPOSITION
7.1.
The
number
II
E
(0,1)
being
fixed,
we
may
find
numbers
fJ,
uE
(0,1)
depending
only
upon
N,p
the
data
and
II,
such
that!orn=O, 1,2,
...
,
either
(7.2)
or
(7.3)
PROOF
OF
LEMMA
5.1:
Iterating (7.2)-(7.3) gives
n=I,2,
....
Since
Yo::;
IK41,
we have only to take
n=no
so large that
uno-I::;
112-
N
•
Then the lemma follows with
2fJ*
=
fJ
no
•
Indeed, Y
no
::;
uno
-1
Yo
implies
meas
{x
E
K2
I
w(x,
t) <
2fJ*}
<
IIIK21.
Recalling the definition (6.4)
of
w and the upper bound (6.11), this in turn yields
(5.14) and concludes the proof
of
the lemma.
7-(i). Proof
of
Proposition
7.1
In (6.10) we take k =
fJ
n
,
n E
N,
where
fJ
E
(0,1)
is
to
be chosen. From the
definition (7.1)
of
Y
n
,
it follows that for every e E
(0,
1)
there exists
to
E
(-4",0),
such that
(7.4)
/
("
(x,
to)
dx
~
Yn+l
-
e.
K4n[W(
·,t
o
)<6
n
+
1
J
The numbers n E N and
to
E (
-4",0)
being fixed, we consider the following two
cases:
either
(7.5)
! /
("
(x, to)
4>6n
(w
(x, to))
dx
~
0
K.
or
(7.6)
! /
("
(x,
to)
4>6n
(w
(x, to)) dx <
o.
K.
In either case we may assume that Y
n
>
II,
otherwise the proposition becomes
trivial. Also, in (7.4) we may take e arbitrarily small within the range
(0,11/2).

8. Proof
of
Proposition
7.1
when (7.6) holds
97
7-(ii). The case (7.5)
If (7.5) holds, it follows
from
(6.10) with k = 6
n
,
that
(7.7)
We
minorise this integral
by
extending the integration over the smaller set
On
such a set
Therefore
(In
1
~
6)
P J
(P
(x,
to)
dx
~
J (P(x, to)!lil
n
(w
(x, to)) dx.
K.n[w(·,t
o
)<6,,+1]
K.
From this, (7.7) and (7.4)
(
1
+6)-P
Yn+1 ~c+C
lnU
.
To
prove the proposition
in
such a case,
we
choose 6 so small that
(
1+6)-P
1/
C
1n-U
~2'
Such a choice depends only
upon
the
constants
"Y,
"Yo
and 1/ and therefore it depends
only upon
the
data.
8. Proof
of
Proposition 7.1 when (7.6) holds
If
(7.6) holds true, define
t.
'"
sup
{t
E
(-4
P
,
to)1
~
1
(P
(x,
t)
<1',.
(w
(x,
t»
<Ix
<'
o}
.
By
the
definition
oft.,
(8.1) J (P (x, to)
4>6
n
(w
(x, to))
dx
~
J (P (x,
t.)
4>6
n
(w
(x,
t.))
dx.
K. K.
By
the arguments of
the
first alternative

98
IV.
flijlder continuity
of
solutions
of
singular parabolic equations
J
("(x,
t.)!lifn (w (x, t.» dx
:5
C
K4
and
VsE
[0,
1J,
J
[
1 6
]-"
("
(x,
t.)
dx
:5
C
In
1
+;
_ s '
K
4
n[(6
n
-w)+>a6
n
J
where
C is
an
absolute constant depending
only
upon
N
and
p
and
the data.
By
the
definition (7.1) of Y
n
,
we
have for all s E [0, 1 J
(8.2) J
("
(x,t.)
dx:5
min
{Yn;
C
[In
1:;
~
sr"}
K4n[(6
n
-w)+
>a6
n
J
{
Yn
= 1 6
-"
C
[ID
Hi-a]
where
s.
is
the
root of the equation
[
1
+ 6
]-"
Yn=Cln
6 .
1 + -
s.
Solving it
we
find
(8.3)
Since Y
n
>v.
we
have
if
0
:5
s <
s.
if
s.
:5
s <
1,
e(c/lI)l/P
_ 1
(8.4)
s.
<
e(CM1/p
(1
+
6)
==
0'0(1
+ 6).
Next
we
estimate the integral on
the
right
hand
side of (8.1).
By
the Fubini theorem
J
("(X,t.)~6n
(w(x,t.))
dx
K4
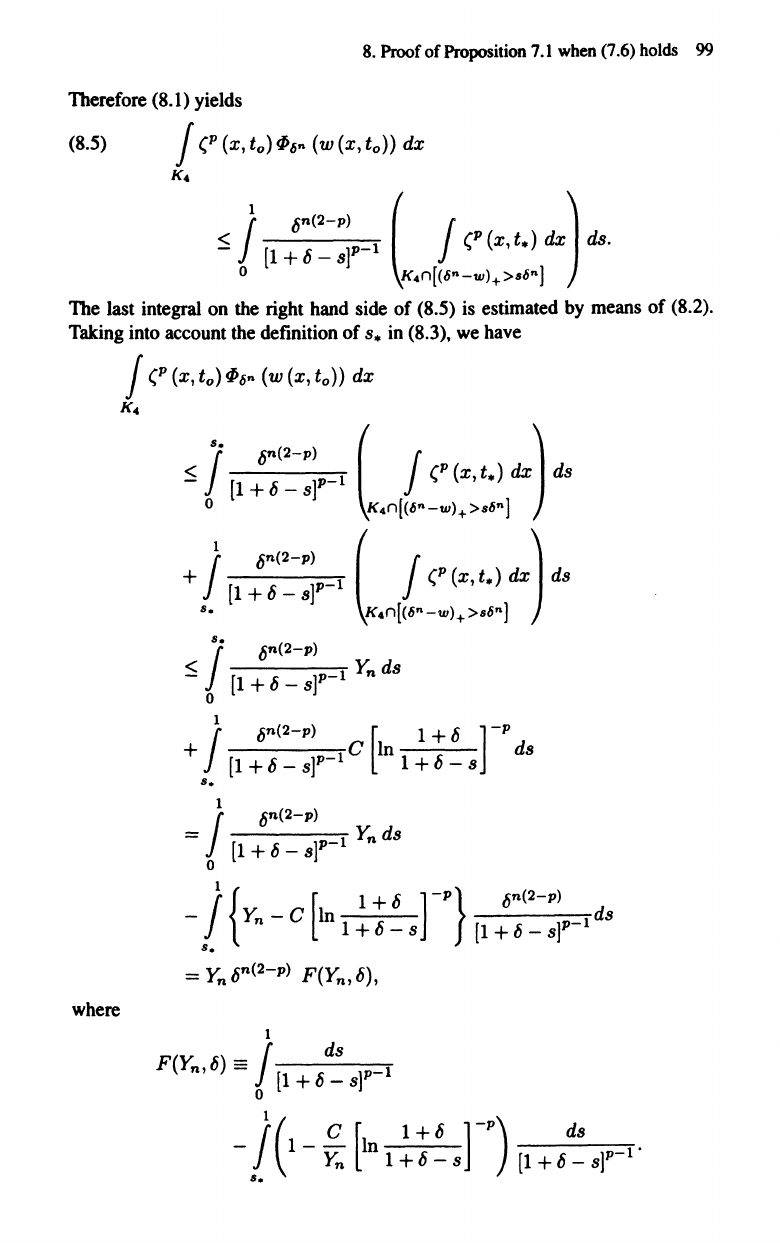
8. Proof
of
Proposition
7.1
when (7.6) holds 99
Therefore (8.1) yields
(8.5) /
(P
(x, to)
~,s"
(w (x,
to»
dx
K"
~
/1
c5
n
(2-p)
P 1 ( /
(P
(x,
t.)
dx)
ds.
[1
+
15
-
s]
o K"n[(,s"-w)+>a,s,,)
The last integral on the right hand side
of
(8.5) is estimated by means
of
(8.2).
Taking into account the definition
of
s.
in (8.3), we have
/
(P(x,to)~,s"
(w(x,to»
dx
K"
B.
/
c5n(2-p)
<
y.
ds
-
[1
+
15
_
sjP-l
n
o
1
/
c5n(2-p)
[ 1 +
15
]
-P
+
GIn
ds
[1
+
15
-
sjP
1 1 +
15
- S
B.
1
/
c5n(2-p)
=
y.
ds
[1
+
c5
_
sIP
1 n
o
/
1 {
[1
+
15
]
-P}
c5n(2-p)
-
y'-Gln
ds
n
l+c5-s
[1+c5-s]P-l
B.
where

100
IV.
Holder
continuity of solutions of singular parabolic equations
From
Y
n
~
v and (8.4) we have
1
F(Y. 6) < / ds
n,
-
[1
+ 6 _
sjP-1
o
_
/1
(1
_ C
[In
1 + 6 ]
-P)
ds .
v
1+6-s
[1+6-sjP-1
0"0(1+6}
These estimates in (8.5) give
1-6
/
/
6n(2-p)
(8.6)
(P
(x,
to)
CP6n
(w
(x, to)) dx
~
Y
n
[1
- /(6)]
p-1
ds,
[1
+ 6 -
s]
K.
0
where
1-6
(8.7)
/
ds
/(6)
[1
+ 6 _ sjP-l -
o
/
1
(1
_ C
[In
1 + 6 ]
-P)
ds
_
/1
ds
v 1 + 6 - s
[1
+ 6 -
S]P-1
[1
+ 6 _
SjP-l
.
0"0(1+6)
1-6
Estimating below the left hand side
of
(8.6) we find
This and
(8.6) yield
(8.8)
Yn+l - e
~
Y
n
(1
-
/(6))
.
We
estimate
/(6)
below. For this let
0"1
~
0"0
be defined by
(see also
(8.4) ) .
Then integrating the first integral on the right hand side
of
(8.7) over the smaller
interval
[0"1(1
+ 6), 1], we derive the estimate
1 (
26
)2-
P
/(6)
>
-(1
- 0"t}2-
p
- - .
2
1+6

9.
Removing the assumption (6.1)
101
We
choose 6 so small that
1 2
/(6)
>
-(1
-
at)
-P
4
and set
1 2
0'
= 1 - 4
(1
-
at)
-p.
Since e E (0, v
/2)
is arbitrary, we obtain from (8.8)
This proves the Proposition
if
(6.1) holds.
9. Removing the assumption (6.1)
Inequality (6.10) holds in any case in the integrated form
t
!
(P~kdx
- !
(P~kdx
+
'Yo
! !
(PtJif
(v )dx $ 'Yh,
K.(t)
K.(t-h)
t-hK.
for all
tE
[-4
P
+
h,
OJ,
h >
O.
We
divide by h and let h - 0 to obtain (6.10) where the term involving the
t-derivative
is replaced by
(d~
) -! (P(x,
t)~k(W)
dx
K.
==
li~~~p
~
{
!(P~k(W)dx
- !
(P~k(W)dX}
dx.
K.(t)
K.(t-h)
Define the set
S
==
{t
E
(-4
P
,0)1
(:r)
-!
(P~k(w)dx
~
o},
K.(t)
and let
to
be
defined as in (7.4).
If
to
E
S,
we have
(9.1)
! (PtJif(v)dx
$'Y.
K.(t
o
)
If
to
¢ S but
sup
{t
<
to
I t E
S}
=
to,

102
IV.
HOlder
continuity of solutions of singular
parabolic
equations
by
working with a sequence of time levels
tn
E
Sand
{tn}-t
o
•
we
see
that (9.1)
continues
to
hold.
If
to
, S and
T = sup
{t
<
to
I t E
S}
<
to,
we
derive
the
two inequalities
J (pl]tr ( w)dx
:5
'Y.
K4(T)
J
(P4>k(w)dx:5
f
(P4>k(w)dx.
K4(t
o
)
K4(T)
The
remainder of the proof remains the
same.
10.
The second alternative
We
assume here that (3.5) holds true for all cylinders
[(x,
0) + Q
(JlP,
doR)]
mak-
ing
up
the partition of Q
(JlP,
CoR).
Since 8
0
~
1
we
have
+-~>
-+~
P.
280
-
P.
2
80
'
so
that
we
may
rephrase (3.5)
as
(10.1)
\(X,
t)
e
[(x,
0) + Q
(RP,
doR)]
I u(x, t) >
p.+
-
2~o
\
<
(1
- 1I
0
)IQ
(RP,
doR)
I,
for all boxes
[(x,O)
+ Q
(JlP,
doR)]
making
up
the
partition
of
Q
(JlP,
coR).
Let n
be
a positive number
to
be selected and arrange that
2na.;z
is
an
integer.
!!!!=.UN
Then
we
combine
2"
of these cylinders
to
form
boxes congruent
to
COR
Figure lO.l
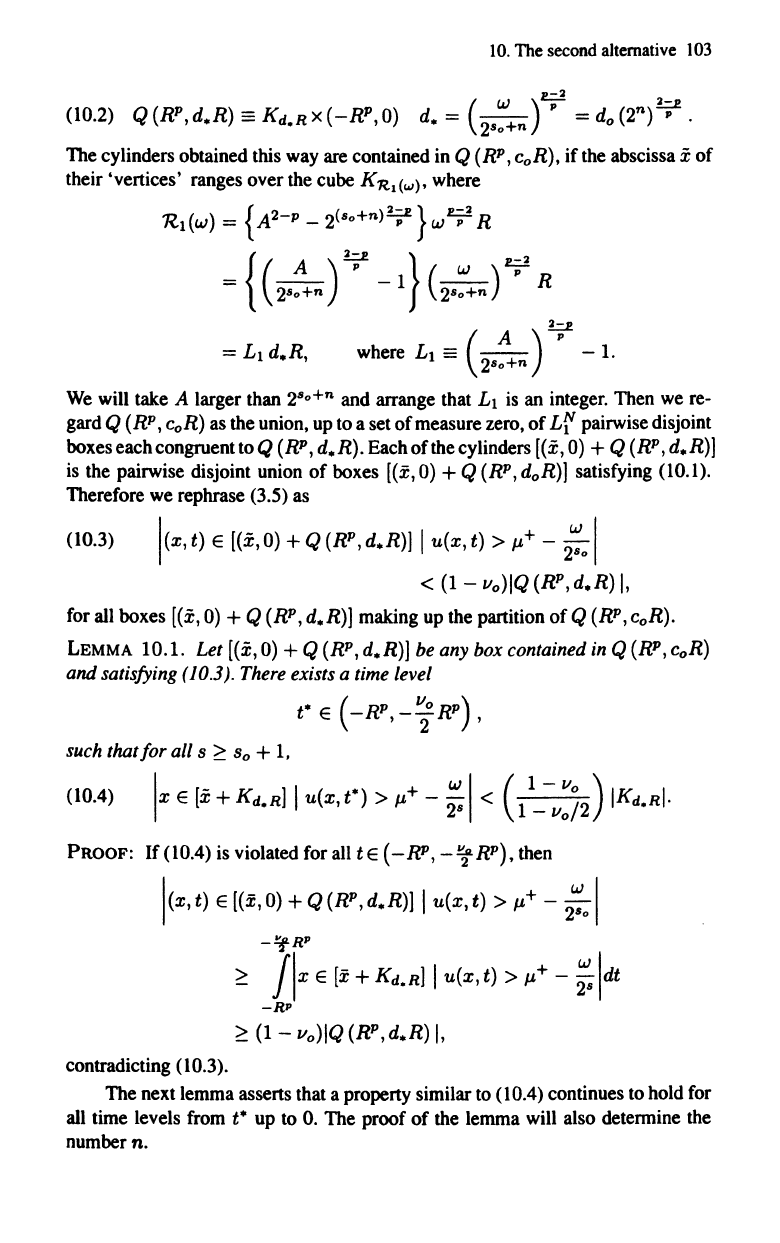
10.
The
second alternative
103
(
w
)~
!.=.I!
(10.2) Q (R", d.R)
==
Kd.R x
(-R",
0) d. = 2
so
+
n
=
do
(2n) p •
The cylinders obtained this way are contained in Q
(RP
,
CoR),
if
the abscissa x
of
their 'vertices' ranges
over
the cube
K'R.l(W)'
where
'R.
1
(w)
=
{A
2
-"
-
2(Bo+n)~}
w~
R
=
--
-1
--
R
{(
A)~
} ( w
)~
2so+n
2
B
o+n
!.=.I!
where
Ll
==
(~)
p - 1.
2
B
o+n
We will take A larger than 2
B
o+n
and arrange that
Ll
is an integer. Then we re-
gard
Q (R",
CoR)
as the union, up to a set
of
measure zero,
of
Lf
pairwise disjoint
boxes each congruent to
Q
(RP,
d.
R).
Each
of
the cylinders
[(x,
0) + Q
(RP,
d.
R)]
is the pairwise disjoint union
of
boxes
[(x,
0) + Q (R",
doR)]
satisfying (10.1).
Therefore we rephrase (3.5) as
(10.3)
I(X,
t) E
[(x,
0) + Q (R", d.R)] I u(x, t) >
p.+
-
2~o
I
<
(1
-
vo)IQ
(R", d.R)
I,
for all boxes
[(x,
0) + Q (RP,d.R)] making up the partition
ofQ
(R",coR).
LEMMA
10.1. Let
[(x,
0)
+ Q (R", d.R)]
be
any
box contained
in
Q
(RP,
CoR)
and satisfying
(10.3).
There
exists a time level
t·
E
(-R"
-
Vo
R")
, 2 '
such
that for all S
~
So
+ 1,
(10.4)
Ix
E
[x
+ Kd.R] I u(x,
t·)
>
p.+
-
;.1
<
(II_-
v
:/
2
)
IKd.RI·
PROOF:
If
(10.4) is violated for all
tE
(-R",
-~R").
then
I(X,
t) E
[(x,
0) + Q (R", d.R)] I u(x, t) >
p.+
-
2~o
I
--1'RP
~
fix
E
[x
+ Kd.R] I
u(x,
t)
>
p.+
-
;.Idt
-RP
~
(1
-
vo)IQ
(R", d.R)
I,
contradicting (10.3).
The
next lemma asserts that a property similar to (10.4) continues to hold for
all time levels from
t·
up
to
O.
The proof
of
the lemma will also detennine the
numbern.

104
IV.
HOlder
continuity of solutions of singular
parabolic
equations
LEMMA
10.2.
There
exists a positive integer n
such
that/or all
t·
< t <0.
(10.5)
Ix
E
[x
+
KdoRll
1£(x,
t) >
p.+
-
2B~+n
I <
(1
-
(~
r)iKdoRI.
PROOF:
Modulo
a translation
we
may
assume that x
==
O.
Consider the logarith-
mic
estimates (3.14)
of
Chap.
II, written over
the
cylinder
KdoR
x (t·, 0),
for
the
function
(1£
-
k)
+ and
for
the levels
W
k=p.+
--.
2
80
As
for
the number c
in
the definition (3.12) of the function IjI
we
take
w
c=--
2
8
0+
n
'
where n
is
a positive number
to
be
chosen. Thus
we
take
(10.6)
where
Ht
==
esssup
(1£-
(p.+
-
~))
.
K"oRX(tO,O) 2 0 +
1be
cutoff function x
-+
((
x)
is
taken so that
{
(
==
1,
on
the cube K(l-u)doR,
0'
E (0,1),
ID(I:5
(O'd.R)-l .
With
these choices, the inequalities (3.14) of
Chap.
II
yield
for
all t* < t <
0,
o
(10.7) j
1j12(x,
t)dx
:5
j
1j12(x,
t*)dx + (ud:R)P j j
1jI1jI~-PdxdT
KCI-")"oR
K"oR
tOK"oR
To
estimate
the
various tenns
in
(10.7)
we
first observe that
'-
W )P-2 [
'-
W
)-1]
IjI
:5
n
In
2,
1jI~-P:5
\2
B
o+
n
'
1 +
InHt
\Fo+R
:51'n In
2.
We
estimate
the
first integral on
the
right
hand
side of (10.7). For this observe
that
IjI vanishes
on
the set
[1£
<
p.+
-
2":0].
Therefore
using
Lemma 10.1,
jIjl2(x,t*)dX:5
n
2
ln
2
2
(/--II:i2)
IKdoRI·
K"oR

10. The second alternative
105
For the second integral we have
1'n
$
uP
IKdoRI·
This estimation justifies the choice
of
the cylinders
[(x,
0) + Q
(RP,
d.R)) over
the boxes
[(x,
0) + Q
(RP,
doR)).
Indeed the integrand grows like 2
n
(2-p)
due to
the singularity
of
the equation. This is balanced by taking a parabolic geometry
!!.1!::.£l
where the space dimensions are stretched by a factor 2 P •
Finally the last tenn on the right hand side
of
(10.7) is estimated above by
where
A2
=
n2(so+n)b
o
and b
o
is defined
in
(3.6). Combining these remarks
in
(10.7) and taking into account (3.7), we obtain for all
t·
< t < 0,
(10.8) f
\li
2
(x, t) dx $ n
2
10
2
2 C
I_-
v
:
i2
)
IKdoRI
+
::
IKdoRI·
K(l-l7)d
o
R
The left hand side
of
(10.8) is estimated below by integrating over the smaller set
{ x E K(l-u)doR I
u(x,
t) >
J.I.+
-
2s~+n
} .
On such a set, since \li is a decreasing function
of
H:,
we estimate
We
carry this
in
(10.8) and divide through by (n -
1)2
10
2
2,
to obtain for all
t·
<
t<O,
Ix
E K(l-u)doR I
1.£(x,
t) >
J.I.+
-
2s~+n
I
$
(n:lr
(11_-
v
:
i2
) IKdoRI+ n:pIKdoRI·
On the other hand
