DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


126
V.
Boundedness
of
weak
solutions
In this section we will show that weak solutions
uEL'oc(nT),
r~
I,
are bounded
provided
p > max {
1;
::
r } .
Such integrability condition to insure boundedness is sharp. In § 12
of
Chap. XII
we produce a solution
of
the homogeneous p.d.e. (1.2)
that is unbounded.(I) Thus in the singular range 1 < p < max
{I;
AZ2}'
the
boundedness
of
a weak solutions is not a purely local fact and,
if
at all true, it must
be deduced from some global information. One
of
them is the weak maximum
principle
of
Theorem 3.3 and Remark 3.1. Another is a sufficiently high order
of
integrability.
5-(i). Local estimates
A sharp sufficient condition can be given in terms
of
the numbers
(5.1)
~r
=
N(P-
2)
+rp,
We
assume that u satisfies
(5.2) u E L'oc(nT), for some r
~
1 such that
~r
>
o.
1be global information needed here is
(5.3)
{
u can be constructed as the weak limit in
L,oc
(n
T
)
of
a
sequence
of
non-negative
bounded
subsolutions
of
(2.8).
The notion
of
weak subsolution requires u to be in the class
By the embedding
of
Proposition 3.1
of
Chap. I, we have
N+2
q=p--.
N
Therefore
ifpis
so close to one that
~q
~o,
the orderofintegrability in
(5.1)-(5.2)
is not implicit in the notion
of
subsolution and must be imposed.
(1)
The
notion
of
solutions
that
are not in
the
function class (2.2) is discussed in
Chap. XII

5.
Homogeneous
structures.
The
singular case 1
<p<2
127
THEOREM
5.1. Let u
be
a non-negative local
weak
subsolution
0/(2.8)-(2.9)
in
nT
and
assume
that (5.2)
and
(5.3)
hold.
There
exists a constant
'Y
=
'Y
(data,
r).
such
that V
[(xo,
to)
+ Q
(9,
p)]
cn
T
andVuE (0,1).
(5.4)
Remark
5.1.
If
9 =
pP,
(5.4) is dimensionless but it is not homogeneous in u.
5-(;;). Estimates near
t=O
Fix
tE
(0, T) and let us rewrite (5.4) for the pair
of
boxes
KTP
x (ut, t),
Kpx
(0,
t).
COROLLARY
5.1.
Let u be a non-negative local
weak
subsolution
of
(2.8)-(2.9)
in
n
T
and let (5.2)-(5.3)
hold.
There
exists a constant
'Y
=
'Y
(data,
r).
such
that
for all
O<t~T
and/or all
uE
(0,1).
(5.5)
'Yt-N/>'r
supu(·,
t)
~
¥.E
K"p
(1-0')
r
Remark
5.2. Assume that (5.2) holds with r =
I,
i.e.,
(5.6)
2N
p>
N+1·
Then the behaviour
of
the supremum
of
u as t
'\.
° is formally the same as that
of
solutions
of
the Dirichlet problem for degenerate equations as in Theorem 4.3.
5-(iii). Global estimates: Dirichlet data
A peculiar phenomenon
of
these equations is that, unlike their degenerate coun-
terparts, local and global estimates take essentially the same form. This appears,
for example, by comparing
(5.5) with the next global estimate.

128
V.
Boundedness
of
weak solutions
THEOREM
5.2. Let
1£
be a non-negative weak subsolution
of
the Dirichlet prob-
lem
(2.5)
and
let (2.6)
and
(5.2)-(5.3) hold. Thereexists a constant'Y =
'Y
(data,
r),
such that
for
all 0 < t $
T,
(5.7)
s~p
u(·,
')
,;
s~~
9 +
,Ni>.
(II
u'
dxdr
)'1>'
6. Energy estimates
The proof
of
the
sup-bounds stated
in the
previous sections
is
based
on
local and
global energy estimates similar
to
those of
§3
of
Chap.
II.
6-(i). Local energy estimates
If
[(x
o
, to)
+ Q
(9,
p)]
c ilT
we
let,
denote a non-negative piecewise smooth
cutoff function vanishing
on
the
parabolic boundary of
[(
x
o
,
to)
+ Q (9, p)].
PROPOSITION
6.1. Let
1£
be a non-negative local weak solution
of
(2.1) in
ilT
and
let (B.)-(B6) hold. There exist a constant
'Y
=
'Y
(data), such that
V [(x
o
,
to)
+ Q (9, p)]cil
T
andfor
every level k > 0
(6.1) sup /
(1£
-
k)!
'''(x,
t)dx + 'Y-
1
jr
riD
(1£
- k)+
,I"dxdr
to-8<t<to
J
[Zo+K,]
[(Zo,t
o
)+Q(8,p)]
$'Y
//(1£
-
k)~
ID,,"dxdr
+'Y
//(1£
-
k)!
,,,-1't
dxdr
[(Zo,t
o
)+Q(8,p)]
[(Zo,t
o
)+Q(8,p)]
{
to
}7It.;(1+1C)
+'Y
/ /
1£6
X.
[1£
>
01
dxdr
+
'Y
/IAt,p(r)jdr
[(zo,t
o
)+Q(9,p)]
to-8
where
It
=
Ito
Ii
and
IAk,p(r)1
==
meas
{x
E
[Xo
+ Kp] I 1£(x,r) > k}.
In (6.1) the integral involving
1£6
can be eliminated if
Ci
= 0, i =
0,1,2,
and
b(x, t,
1£,
D1£)
==
O.
Moreover the last term can be eliminated
if!pi
==
0, i = 0,
1,
2.
PROOF:
The proof
is
very similar
to
that
of
Proposition
3.1
of Chap. II. First
we
may
assume that (x
o
,
to)
==
(0,0) modulo a translation. Then
in
(2.3)
we
take
the
testing functions
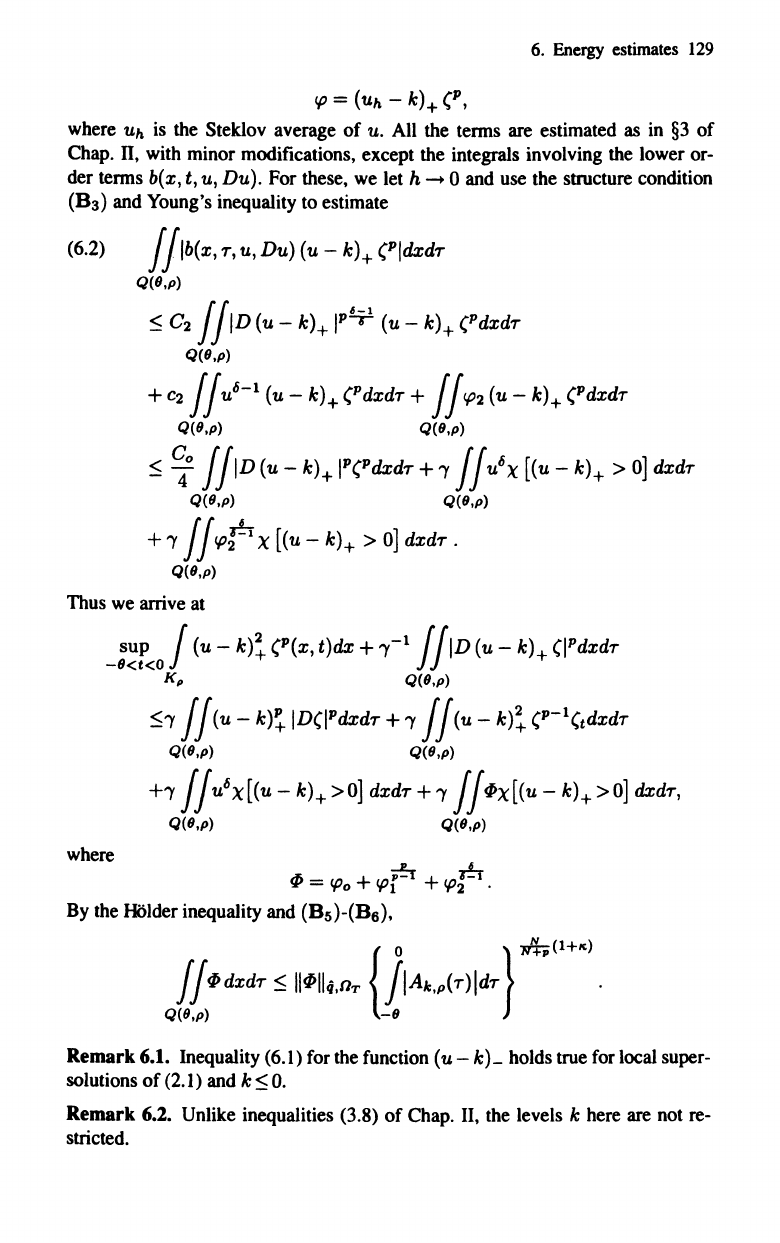
6.
Energy
estimates
129
cP
=
(Uh
- k)+ (II,
where
Uh
is the Steklov average
of
u. All the terms are estimated as in
§3
of
Chap. II, with minor modifications, except the integrals involving the lower or-
der terms
b(x,
t,
u, Du). For these, we let h - 0 and use the structure condition
(B3) and Young's inequality to estimate
(6.2) I
jlb(x,
r,
u,
Du)
(u - k)+ (1Ildxdr
Q(9,p)
:5
C
2
I
liD
(u - k)+ I
P
¥ (u - k)+
(/dxdr
Q(9,p)
+C2
Ilu
6
-
1
(u-k)+(Pdxdr+
Ilcp2(U-k)+(PdXdr
Q(9,p)
Q(9,p)
:5
~o
I
liD
(u - k)+ IP(Pdxdr +
'Y
II
u
6
')(
[(u - k)+ >
0]
dxdr
Q(9,p)
Q(9,p)
+
'Y
I I
cpr')(
[(u - k)+ >
0]
dxdr
.
Q(9,p)
Thus we arrive at
sup I (u -
k)!
(P(x,
t)dx
+ 'Y-
1
r
riD
(u - k)+ (IPdxdr
-9<t<O
JJ
Kp
Q(9,p)
:5'Y
II(u
-
k)~
ID(IPdxdr +
'Y
II(U
-
k)!
(P-l(t
dxdr
Q(9,p)
Q(9,p)
+'Y
II
u
6
')([(u
- k)+
>0]
dxdr
+
'Y
II
~')([(u
- k)+
>0]
dxdr,
Q(9,p) Q(9,p)
where
..r;.
+;;!:r+
6
~
=
CPo
CP1
CP2·
By the
HOlder
inequality and (B5)-(B6),
{
0
}~(1+IC)
II~dxdr:5
"~"q,nT
IIA/c,p(r)ldr
Q(9,p)
-9
Remark
6.1. Inequality (6.1) for the function (u - k)_ holds true for local super-
solutions
of
(2.1) and k:5
o.
Remark
6.2. Unlike inequalities (3.8)
of
Chap. II, the levels k here are not re-
stricted.

130
V.
Boundedness
of weak
solutions
6-(ii}.
Global energy estimates: Dirichlet
data
PROPOSITION 6.2. Let u be a non-negative
weak
sub-solution
of
the
Dirichlet
problem
(2.5), let (2.6) hold and let k satisfy
(6.2)
k
~
supgAO.
ST
There
exists a constant
'Y
=
'Y
(data),
such
that for
every
non-negative
function
t--+(t) eC1[0,
T]
andfor
every
O<t~T,
(6.3) sup
!(u-k)!(T)dx+
ffID(u-k)+IP(T)dxdT
O<T<t
11
n
n,
~'Y
!(Uo-k)!(O)dx+'Y
!!(u-k)!(t(T)dxdT
n
n,
(t
)4(1+1C)
+'Y
If
u6x
[u
>
k]
(T)dxdT+'Y
~IA1c'P(T)I(T)dT
where
1£
=
1£0
Ii,
and
IA1c,p(T)1
==
meas
{x
e U I U(X,T) >
k}.
In
(63)
the
integral involving u
6
can
be eliminated
if
£1=0,
i=0,1,2,
and b(x,
t,u,
Du)
==0.
Moreover
the
last
term
can
be eliminated
ifIPi==O,
i=O,
1,
2.
A similar statement
holds
for the truncatedfunctions (u - k)_ provided
(6.2)'
k < infgVO.
-
ST
PROOF:
If k satisfies (6.2),
by
Lemma
2.1
of Chap. I
(uhht)
- k)+ E W!,P(U),
Therefore
the
testing functions
VO<t~T-h.
are admissible in the weak fonnulation
of
the Dirichlet problem.

7.
Local iterative inequalities
131
7.
Local iterative inequalities
The
common
element
in the
proof of the sup-bounds stated
in
§3
and
4
is
a
set
of
iterative inequalities.
We
will
derive
them,
starting
from
the
energy
inequalities of
§6.
Modulo
a translation,
we
may
assume
that
(xo,
to)
coincides
with
the
origin.
Fix
q E
(0,
1)
and
consider
the
sequences
(l-q)
(l-q)
Pn
=
qp
+ 2 p,
(In
=
q(J
+
(J,
n = 0,1,2,
...
,
n 2n
and
the
corresponding cylinders
QniEQ
((In,
Pn). It
follows
from
the
definitions
that
Qo
= Q
«(J,
p),
and
Qoo
= Q
(q(J,
qp)
.
Consider also the
family
of
boxes
where
for
n=O,I,2,
...
_ .
Pn
+
Pn+l
3(1 - q)
Pn
= 2
=qp
+ 2n+2 p,
For
these
boxes
we
have
the inclusion
Qn+lCQnCQn,
Introduce the
sequence
of increasing levels
n = 0,1,2,
....
k
=k-~
n 2
n
'
where
k
is
a positive number to
be
chosen.
We
will
work
with
the
inequalities (6.1)
written
for
the
functions
(u - kn+l)+, over
the
boxes
Qn.
The
cutoff
function
(
is
taken to satisfy
{
(
:ani~hes_on
the
parabolic
boundary
of Qn,
(=
1
10
Qn,
I
D'"I
< 2"+2 0 < < 2"+2
':.
-
{1-a)p'
-
(t
-
(l-a)B"
With
these choices, (6.1)
yields
(7.1) sup
j(u
-
kn+l)!
(P(x, t)dx +
{{ID
(u -
kn+l)+
(I
P
dxdT
-8,,<t<O JJ
Kp.. Q ..
-y2
np
{{
~
(1-
q)ppp
J J (u -
kn+tl~
dxdT
Q
..
+
(1
~:)(J
j
j(u
-
kn+l)!
dxdT
Q
..
+-y
jju
6x
[(u -
kn+tl+
>
0]
dxdT+-yIA
n
+llllh(1+
IC
),
Q
..
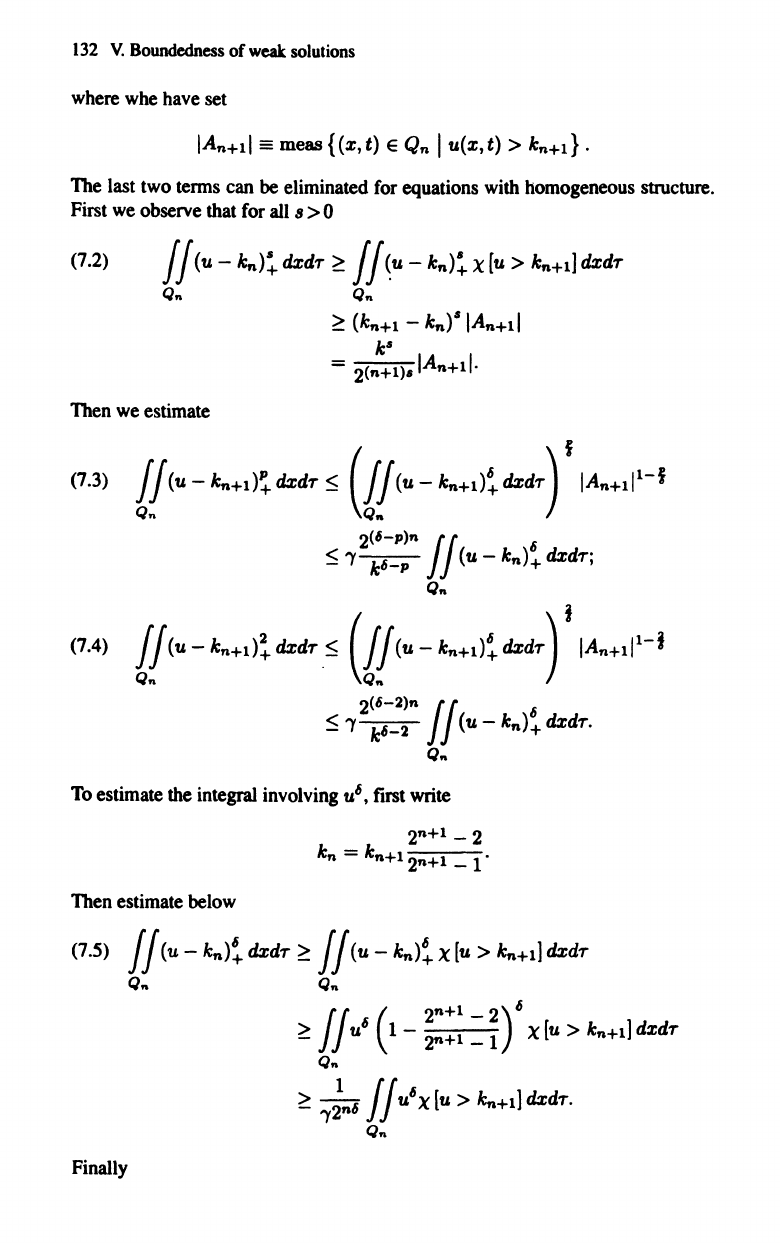
132
V.
Boundedness
of
weak
solutions
where
whe
have
set
IAn+l1
==
meas{(x,t) e
Qn
I
u(x,t)
>
kn+l}'
The
last
two
tenns
can
be
eliminated
for
equations
with
homogeneous
structure.
First
we
observe
that
for
all
8 > 0
(7.2)
II(u
-
kn)~
dxdT
~
II~u
-
kn)~
X
[u
>
kn+l]dxdT
Qn
Qn
Then
we
estimate
~
(kn+l - k
n
)'
IAn+l1
k'
= 2(n+l),IA
n
+
1
1.
To
estimate
the
integral involving u
6
,
first
write
2
n
+l - 2
k
n
= kn+l2n+l
-1'
Then
estimate
below
(7.5)
II(u
-
kn)~
dxdT
~
II(U
-
kn)~
X
[u
> kn+l] dxdT
Qn Qn
~
IIu
6
(1-
~::
=~)6
X[u
> k
n
+l]dxdT
Qn
~
'Y:
n6
II
u
6
X
[u
> kn+l] dxdT.
Qn
Finally

7.
Local iterative inequalities
133
We
combine these estimates into (7.1)
to
derive the following basic iterative
in-
equalities
Moreover the last two tenns can
be
eliminated for equations with homogeneous
structure.
To
proceed, construct a non-negative piecewise smooth cutoff function (n
in
Qn, which equals one on Qn+l, vanishes
on
the lateral boundary of
Qn
and
such
that
ID(nl
$ 2
n
+
2
/(1
- u}p.
Then the function (u - kn+l)+ (n vanishes
on
the lateral boundary
ofQn
and
by
the
multiplicative inequality
of
Proposition
3.1
of
Chap.
I,
(7.7) /
/(u
-
kn+l)~
(!dxdT
$
'Y
(_sup
/ (u _
kn+l)!
dx)
i
-
-9,,<t<OK
~
~
x
(i/ID(U-kn+d+IPdXdT+
i/(U-kn+l)~ID(nIPdxdT).
Q"
Q"
Remark
7.1. The estimates
in
(7.2)-(7.5) and
the
inequalities (7.6), (7.7)
are
valid for any number
6
~
max{pj 2}.
The structural restriction 6 = q
does
not
play
any
role
in
the derivation of (7.6)
and
(7.7).
134
V.
Boundedness
of
weak
solutions
8.
Local iterative inequalities
(P>
max
{
1;
&~2
} )
Introduce
the
dimensionless quantities
(8.1)
Y
n
= H (u -
kn)~
dxdr,
n = 0,1,2,
....
Qn
We
will derive
an
iterative inequality for Y
n
by
estimating the right hand side of
(7.7)
by
(7.6).
We
assume first
{
2N}
N+2
(8.2)
p >
max
1 j N + 2 '
max{pj
2}
~
6 < q
==
P-r
and estimate
Yn+l
~
'Y
H (u -
kn+l)~
(!dxdT
Qn
We
estimate
the
last integral
by
(7.7)
and
in
turn
estimate
the
right hand
side
of
(7.7)
by
the inequalities (7.6)
and
(7.3).
We
arrive
at
the
recursive inequalities
(8.3)
Yn+l <
'Y
bn
~
.A!*
Y,!'+~*
-
k~(q-6)
(1
-
O')P~
b
n
(
N(J)~*
1...2.
I.
(1
)l+~"
+
'Y
P
y'l+,N
+"Vbn
(pN(J)'"
-y.
k~(9-6)
n,
k
6
n ,
where
and
(8.4)
.A..
..
(
(;)
kqz(P-'l +
(~)
f kqz(2-'l).
The last
two
tenns
in
(8.3) can
be
eliminated
for
solutions of equations
with
ho-
mogeneous structure.
9. Global iterative inequalities 135
9.
Global iterative inequalities
We
let u
be
any
non-negative
weak
subsohition of
the
Dirichlet
problem
(2.5)
and
assume
that
(6.2)
holds
so
that
u satisfies
the
energy
estimates
(6.3).
Fix
0 < t
~
T
and introduce
the
sequence of increasing
time
levels
tn
=
ut
(1
-
2:
),
u E (0,1), n = 0,1,2,
...
,
and
the
cutoff
functions
iftn+l~T~t
if
tn
< T < tn+l
Introduce also
the
sequence of increasing
levels
k
k
n
= sup 9 + k -
-2'
n =
0,
1,2,
...
, k > 0 to
be
chosen
ST
n
and
write
(6.3)
for
the
functions
(u - kn+d +
and
the
cutoff
functions
(n
to
obtain
t
(9.1)
sup
/(u
-
kn+l)!
dx + /
"n
(u - kn+l)+
IPdxdT
t,,+1 <T;St J "
II
t,,+lll
t t
~
'Y::
/
/(U
-
kn+d!
dxdr +
'Y
/
/u6x
[u
> kn+lJ
dxdT
t"ll t"ll
where
we
have
set
The
last
two
terms
of
(9.1)
can
be
eliminated
for
equations
with
homogeneous
structure. Moreover
the
last
term
can
be
eliminated
if
in
the
structure conditions
(B
1
)-(B3),
!Pi
::0,
i=O,I,2.
If
!Pi
E
LOO(nT),
i=O,l,
2,
then
It=
N'
Proceeding
as
in
(7.2)-(7.5),
we
estimate
