DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


146
V.
Boundedness
of weak
solutions
This inequality holds for all
fJ,p,u
for which (15.1) is verified. It also holds for
any pair
of
boxes
[(x
o
,
to)
+ Q
(fJ,
p»)
and
[(x
o
,
to)
+ Q
(ufJ,
up)]
,
with arbitrary 'vertices' provided they are contained in E
T
•
Fix any
te
(0, T) and
introduce the boxes
and
Kp/2
x
Ut,
t}.
We
rewrite (15.3) and (15.1) in terms
of
these cylinders, for which
u=
t.
LEMMA 15.1. Forallte(O,T)andp>Ojorwhich
(15.4)
( )
-(,,-2)
t
~
21'-1", sup u(x, t) ,
K,,/3
tMreholds
(15.5)
~~~
u(x, t)
~
'Y
(~)
N/IA
(j
f
UpdxdT)
p/IA
t/'lK"
For r > 0 introduce the quantity
(15.6)
f(t)=
sup {TN/Asupllu(.,T)lIoo,K,,},
~=N(P-2)+p.
O<.,.<t
p~.,.
p'tbs
By possibly working within the time. interval (e,
T)
and then letting e
'\,
0, we may
assume that f(t) is finite. This follows from Theorem 4.4. Let
t*
e (0,
T)
be
the
largest time level for which
(15.7) t
p
/
A
~
2" [f(t)]-(p-2) ,
VO
< t
~
t*.
The knowledge
of
t*
is only qualiwive. Shortly we will find a quantitative upper
bound for
t*.
Here we remark that owing
to
the definition
of
f (t) the condition
(15.4) holds for all p > r and all t e (0,
t*).
Consequendy (15.5) holds for all
t e (0, t*].
We
estimate the integral on the right hand side
of
(15.5) as follows
t t
1'-1
ff
UPdxdT
~
p~
f
(lI
u
(.,T)lI
oo
,K,,)
f
U(X,T)
dxdT
p'tbs pN+'tbs
t/'lK,.
t/2
K,.
<
(
2)~
£:, {
N/A
lIu(.,Tlloo,K,.
},,-1
_ - PP- sup T sup
.....IL
t
O<.,.<t
p~r
pP-'2
X { sup sup f
~:'1
dxdT}
o<.,.<t
p~r
K p
P-
"
~
=
(~).
p~
fp-l(t)
Ilull{r,t}

16.
Proof of Theorems
5.1
and
5.2
147
where the nonn
11·II{r,t}
is defined in (4.4). Putting this estimate in (15.5) gives
.
sup
u(x
t) <
"Y
p-t!:rJ
!(t)P(P-l)/"
IlluII
P
/"
.
K
,-
t
N
/>..
{r,t}
,,/2
We divide by (p/2)p/(p-2) and multiply by t
N
/>...
Then take the supremum for
p>
r and use the fact that t E (0,
t·)
is arbitrary to deduce
'VO
< t:S
t*,
i.e.,
(lS.S)
'VO
< t
:S
t·.
Thus it follows from (15.7) that (15.S) continues
to
hold for all 0 < t
:S
t., where
II
11
-(p-2)
t.
=
"Y.
u
{r,t"}
.
16.
Proof of Theorems
5.1
and
5.2
We
first prove Theorem
5.1
for the case when the assumptions
(5.1
)-(5.2) hold for
some
1:S r:S 2.
In
such a case we have
p>
max
{
1;
J~2}'
and we may use the
iterative estimates (S.3).
In
these we discard the last two tenns and take 6 =
2.
We
also stipulate to take
1
k>
-
sup
u
- 2
Q(ulJ,up)
and arrive at
y.
<
"Y
bn
A~Ny'l+~N
6 =
2,
n+l
- ! JII±,
!(
6)
-"'tT
n ,
(1-
u)P,-W-k,
q-
where
{
[
]
(p-6)~
Ii.}
.Au
=
(~)
sup
u p +
(~)
p ,
p'P
Q(ulJ,up)
6=2,
and Y
n
are defined in (S.l).
By
Lemma 4.1
of
Chap. I, Y
n
-+
0 as n
-+
00,
provided
we choose
k from
Yo
==
if u
2
d.xdr = C
(1-
u)N+p
A;lk~(q-6),
Q(IJ,p)
for a constant C depending only upon the data. This implies

148
V.
Boundedness
of
weak solutions
(16.1)
"YA,~
sup u:5
~
Q(fTlJ,fTp)
(1
-
u)"N"('9-Tf
6=2.
We
conclude the proof for the case r E
[1,
2)
by means
of
an
interpolation process
similar to that
of
Lemma 4.3
of
Chap. I; namely, consider the sequences
Pn,
9
n
and the corresponding cylinders
Q(n)
==
Q
(9
n
,
Pn), introduced in (12.4)-(12.5).
Define also the numbers
Mn
as in (12.6), and write (16.1) for the pair
of
boxes
Q(n)
and
Q(n+l).
This gives
"Y
2n
"
Nft-.
p
,)
A~
If 2
(
)
~
(16.2) Mn:5
~
U
dxdT
(1
- u)"
q-
Q(
..
+1)
where
Consider the two terms making up
An.
If
for some n = 0,
1,2,
...
the first term
dominates the second, we have
(16.3)
(
9)
1/(2-,,)
Mn<
-
-
pP
and there is nothing
to
prove. Otherwise, (16.3) fails for all
n=O,
1,2,
...
and
n=0,1,2,
....
We
deduce from (16.2)
"Y2n,,~
~
(PP)~
If r
(
)
~
Mn
:5
~
Mn+l
7i U
dxdT
(1
-
u)"
q-
Q(
..
+l)
The proof is now concluded as in Lemma 4.3
of
Chap. I.
The proof
of
Theorem
5.1
for the case r > 2 is
based
on
the recursive inequal-
ities
(10.4). As before, we stipulate to take
and majorise
Ble
by
where
1
k>
- sup
u.
- 2 Q(fTlJ,fTp)
B <
k(2-r)~B
Ie
_
fT'

17. Natural growth conditions 149
B.
~
{
(;)
[Q(:~pA'-2)~
+
(~)
~}
With these choices, we obtain from (10.4) the recursive inequalities
y;
<
'"'(bnB!
II II
r
-
q
y;l+i
n+l
-
(1
_
u)i(N+p)k(r-2)!!p
u oo,Q(8,p) n .
By Lemma 4.1
of
Chap. I, Y
n
-+
0 as n
-+
00,
provided
y; =
jfurdXdT
=
C(I-
u)N+PB-lk(r-2)~llull(q-r)~
o - u oo,Q(8,p) '
Q(8,p)
for a constant C depending only upon the data. Thus
(16.4)
sup
u
Q(u8,up)
(
)
(r
2jfR+pj
<
'"'(
B(r
2jfN+pj
lIull~~
jfurdXdT
-
(1
_ u);:!, u oo,Q(8,p)
Q(8,p)
Let
Q(n)
=Q(On,
Pn)
and Mn be defined as in (12.4)-(12.6). Then from (16.4)
where
B.~
{(;)M~-2)~
+
(~)~}
The proof is now concluded as in the case r E
[1,
2).
The proof
of
Theorem 5.2 is essentially the same.
IfrE
[1,2), it follows from
the recursive inequalities (9.4).
If
r > 2, we start from the global inequalities (10.6).
17.
Natural growth conditions
Consider the Dirichlet problem
(17.1)
{
Ut
-
divlDul
p
-
2
Du
= IDuI
P
,
in
nT,
p>
I,
ul
r
= I E
LOO(r),
where r denotes the parabolic boundary
of
nT.
The lower order term has the
'natural'
or
Hadamard growth condition with respect to IDul (see [48]). The notion

150
V.
Boundedness
of
weak solutions
of
weak
solution
is
that of
§2
of Chap.
II. Here
we
stress that if
we
merely require
that
IDul
E VenT), the testing functions must
be
bounded
to
account
for
the
growth of
the
right hand side.
The problem
we
address here
is
that of finding a sup-bound for a solution u.
It
is
known that weak solutions of (17.1)
in
general
are
not bounded, not even
in
the
elliptic case (see
[15]).
This
is
due
to
the fast growth of the right hand side
with
respect
to
IDul.
On
the other hand the existence theory is
based
on
constructing
solutions
as
limits,
in
some appropriate topology, of bounded solutions of
some
sequence of approximating problems. The limiting process is possible if
one
can
find
a uniform upper bound on the approximating solutions. Therefore the main
problem regarding sup-estimates for solutions of (17.1) can
be
formulated
as
fol-
lows.
Assuming that a
weak
solution u of (17.1)
is
qualitatively bounded,
find
a quantitative
VlO
(n
T
)
estimate, depending only
upon
the data. In such a
form,
the problem
was
fust formulated
by
Stampacchia
[93]
in
the context of elliptic
equations.
THEOREM
17.1. Let u
be
a
bounded
weak
solution
of
(17.1
).
Then
07.2)
lIulloo,aT
:S
F =
IIflloo,r·
PROOF:
By
working with u+ and
u_
separately,
we
may
assume that u
is
non-
negative. Set
M
= esssupu.
aT
If
M > F,
in
the
weak
formulation
of
(17.1)
we
take the testing functions
(u -
k)+,
where k = M - E
~
F,
for
some
E>O,
modulo a Steklov averaging process. These
are
admissible since
they
vanish on
the parabolic boundary
of
n
T
and are bounded.
We
obtain
esssup
! (u -
k)!
dx + f f ID (u - k)+ I"dxdr
O<T<T
11
nx{T}
aT
:s
! J ID (u - k)+
I"
(u - k)+ dxdr
aT
:S
E !! ID (u - k)+ I"dxdr.
aT
Thus if
EE
(0,1),
we
have (u - k)+
=0
in
nT
and
esssupu:S
M - E.
aT
This contradicts
the
definition of M and proves the theorem.
COROLLARY
17.1.
Assume
f =
O.
Then
(17.1)
does
not
have
any non-trivial
bounded
weak
solution.

17.
Natural
growth
conditions
151
17-(i). General structures
More generally
we
may
consider the Dirichlet problem
{
u
E C (0,T;L2(n»)nLP
(0,
T;
Wl,p(n))
,
(17.3)
Ut
- div a(x,
t,
u,
Du) =
b(x,
t,
u,
Du)
in
nT,
ul
r
= I E
LOO(r),
where the p.d.e. satisfies
the
sbUcture
conditions
(Bi)
(B;)
a(x, t,
u,
Du) . Du
~
ColDul
P
-
<Po
(x, t),
Ib(x,
t,
u,
Du)1
5 C
2
1Dui
P
+
<P2(X,
t).
The lower order
tenDs
have the Hadamard 'natural' growth condition.
Here
C
i
,
i =
0,2,
are
given positive constants and the non-negative functions
<Pi,
i = 0,
2,
sat-
isfy
(Bs)
where
(B
6
)
1 P
-:
=
(I-lI:o)-N
..
q
+p
11:0
E (0,1).
THEOREM
17.2.
Let u
be
a qualitatively bounded weak solution
of
(17.3)
in
nT.
There
exists a constant C that
can
be
determined quantitatively a priori only
in
terms
of
the
data.
such
that
PROOF:
As
before
we
may
assume that u
is
non-negative.
If
M
is
the
essential
supremum of u
in
nT,
we
may assume that M >
211/I1oo,r;
otherwise there
is
nothing to prove. In the weak formulation
of
(17.3),
we
take the testing function
(u -
k)+, where
Il/lIoo,r
5 k <
M.
This is admissible, modulo a Steklov averaging process, since it
is
bounded and it
vanishes in
the
sense of
the
traces on the parabolic boundary of n
T
•
Calculations
in all analogous to those in §4-(ii) of Chap.
II
give
(17.4)
sup
I (u -
k)!
dx
+
Co
Jr
[ ID (u - k)+
IPdxdT
O<t<T 2 J
l1x{t}
aT
5
C2
II
ID(u
- k)+ IP(u - k)+dxdT
aT
+
'Y
II
{<Pox
[u
>
k)
+
IP2
(u
-
k)+}
dxdT.
aT
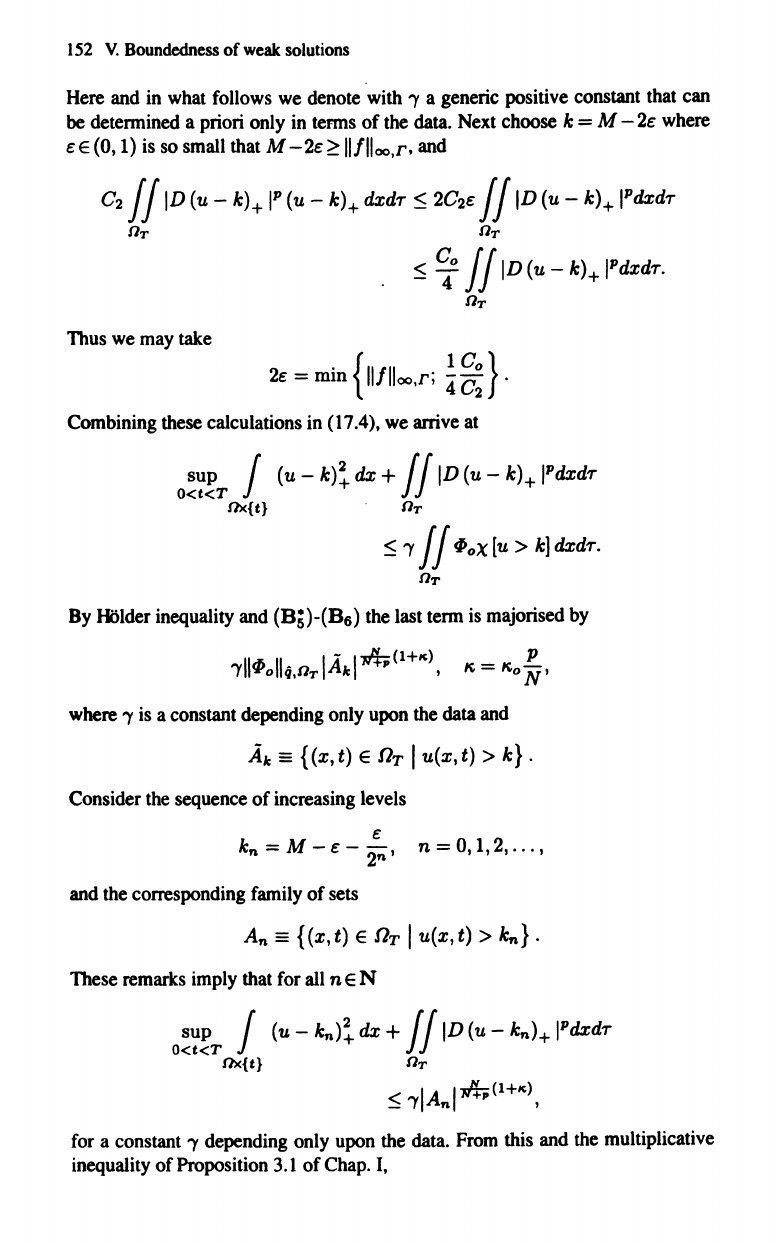
152
v.
Boundedness of
weak
solutions
Here and in what follows
we
denote with
'Y
a generic positive constant that can
be
detennined a priori only in tenns
of
the data. Next choose k = M -
2E
where
EE
(0,1)
is so small that M
-2E
~
IIflloo,r,
and
C
2
II ID (u - k)+
IP
(u - k)+
dxdT
~
2C2E
II ID (u - k)+
IPdxdT
aT aT
~
~o
II ID (u - k)+
IPdxdT.
aT
Thus we may take
2E
=
min
{lIflloo,ri
~
g:
} .
Combining these calculations in (17.4), we arrive at
sup
I (u -
k)!
dx
+ f f ID (u - k)+
IPdxdT
O<t<T
11
ax{t}
aT
~
'Y
I I "oX
[u
>
k]
dxdT.
aT
By HOlder inequality and
(B
5
)-(B
6
)
the last
tenn
is majorised by
where
'Y
is a constant depending only upon the data and
Ale
==
{(x,t)
E n
T
1
u(x,t)
> k}.
Consider the sequence
of
increasing levels
E
k
n
= M - E - 2
n
'
n = 0, 1,2,
...
,
and the corresponding family
of
sets
An
==
{(x,t)
E n
T
1
u(x,t)
>
len}.
These remarlcs imply that for all n E N
sup
I (u - k
n
)!
dx
+ f f ID (u - k
n
)+
IPdxdT
O<t<T
11
ax{t}
aT
<
IA
1
4
(1+1()
_
'Y
n ,
for a constant
'Y
depending only upon the data. From this and the multiplicative
inequality
of
Proposition 3.1
of
Chap. I,
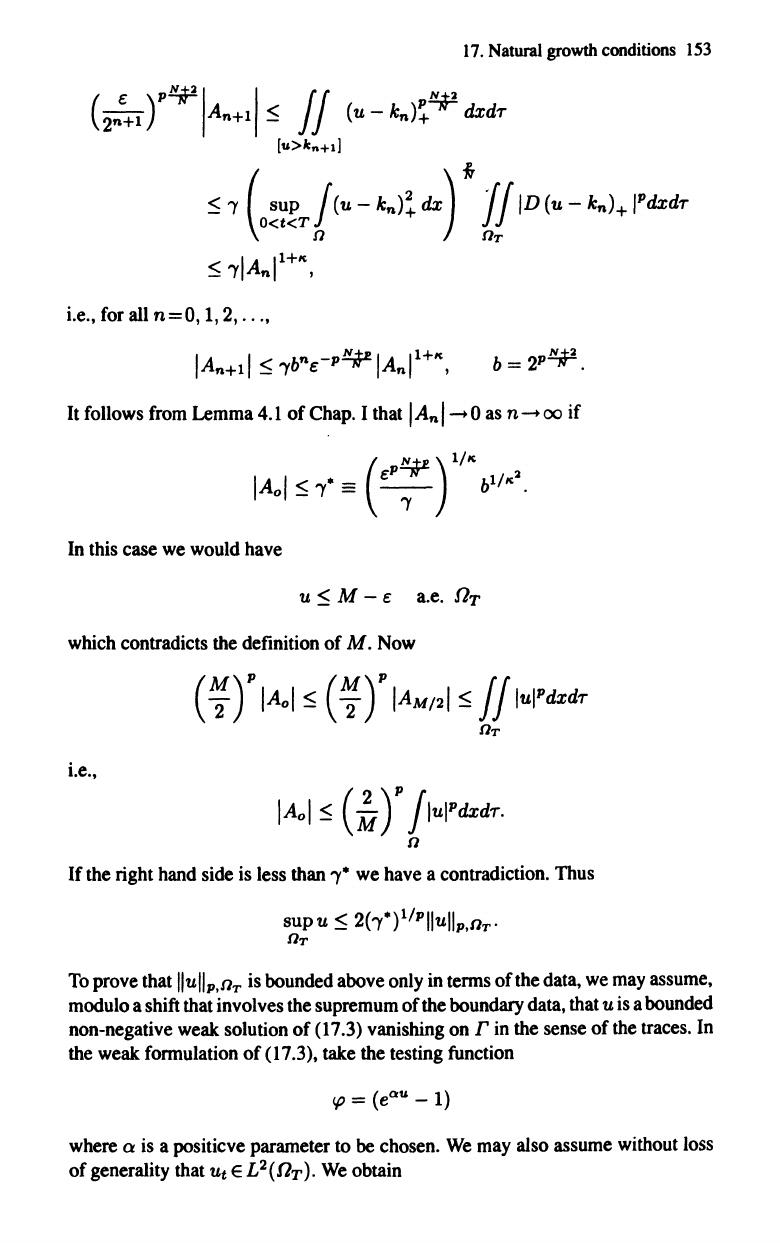
17.
Natural
growth
conditions
153
i.e.,
for
all
n=O,
1,
2,
...
,
IA
I
< b
n
-p!:!..p.IA
1
1
+1<
n+1
_
"1
en,
b=2p~.
It follows
from
Lemma 4.1 of
Chap.
I that I
An
1-0
as
n -
00
if
In this case
we
would
have
u~M-e
a.e.
aT
which
contradicts the definition of
M.
Now
i.e.,
IAol
~
(!) p
j1ulPdxdr.
n
If the right
hand
side is less than
"1.
we
have a contradiction.
Thus
To
prove that
lIullp,nT
is bounded above only
in
terms of the data,
we
may
assume,
modulo a shift that involves the supremum of the boundary
data, that u
is
a bounded
non-negative
weak
solution
of
(17.3) vanishing on r
in
the sense of
the
traces. In
the
weak formulation
of
(17.3), take the testing function
cp
= (e
QU
-1)
where Q
is
a positicve parameter
to
be
chosen.
We
may
also assume without
loss
of generality that
Ut
E
L2
(aT).
We
obtain

154
V.
Boundedness
of
weak
solutions
j !
I(j
(e
OS
-1)ds)
dxdr
+ Q
III
DulPeoudxdr
o a 0
at
:S
O
2
IltDulPeOUdxdr
+
'Y
11(1
+
CPo)
eoudxdr,
at at
for
a constant
'Y
=
'Y
(data)
and
for
all
t E
(0,
T).
We
choose Q = 202
and
set
to
obtain
IIwllt-p(aT)
:S
'Yo
+
'Yl
II
(1
+
CPo)
wPdxdr,
aT
for
two
constants
'Yi
=
'Yi
(data) , i=O,
1.
Next
by
(Bs) -
(B
6
),
11(1
+
CPo)
wP-dxdr
aT
Moreover
since
w(·, t)
vanishes
om
on
for
a.e.
t E
(0,
T),
by
the embedding of
Proposition
3.1
Chap.
I,
IIwll:~.aT
:S
'Yllwllt-p(a
T
)'
'Y
=
'Y
(data) .
Combining
these
remarks
in
(17.5)
we
conclude
that
there exist
two
constants
C
o
,C
1
,
depending
only
upon
the
data
such
that
IIwll:~.aT
:S
Co
+Clln,.I~lIwll:~.aT·
If T
is
so
small
that,
say
then
IIwll:~.aT
:S
2C
o
•
For arbitrary
T>
0,
the
argument
can
be
repeated
up
to covering
the
whole
flT
in
a
finite
number
of
steps.

18. Bibliographical notes
155
18. Bibliographical notes
The
sup-bounds of
§3
are essentially due
to
Porzio
[87].
They
follow
a parabolic
version of
DeGiorgi
iteration technique (see
[67])
and
remain valid
even
in the
'linear' case p =
2.
An
effort
has
been
made
to
trace
the
dependence of
the var-
ious constants
upon
the
size
of
the
domains
where
the
estimates are derived.
We
have also computed
how
the
various estimates deteriorate
when
t
-+
O.
In
the
case of homogeneous
sbUctures
for
degenerate equations (see
§4),
the
interpo-
lation estimate (4.1)
is
of particular interest. It reveals a behaviour dramatically
different
from
the
linear case
p=
2.
An
estimate of
this
kind
(i.e.,
for
small
e)
had
been proved
by
Moser
[83]
for
solutions of linear parabolic equations
with
mea-
surable coefficients. Generalizations
to
quasilinear equations with 'linear'
growth
p = 2
are
in
[7,97].
The
global estimates
in
ET
of
§4-(IV)
are
taken
from
[41].
We
have given a different
and
simpler proof. For
the
porous
medium
equation
with
power-type non-linearities, estimates of
the
same
nature have
been
proved
by
BtSnilan-Crandall-Pierre
[10].
Analogous estimates
for
general non-linearities
appear
in
[4].
Still in
the
context
of
the
porous
medium
equation, rather precise
local sup-estimates have
been
recently obtained
by
Andreucci
[3].
For equation
with
singular structure (1 < p <
2),
the theory of
local
and
global
boundedness
has
started
only
recently
in
[42]
and
[43].
Improvements
to
equations
with
general
structures
are
in
[87].
The
results of Theorems 5.1-5.3
are
sharp.
They
will
play
a central role
in
the
Harnack estimates of
Chap.
VII.
The integrability condition
(5.2)
is
sharp
as
shown
by
the
counterexample
in
§
13
of
Chap.
XII.
The
arguments
of
§17
appear
in
[101].
