DiBenedetto E. Degenerate Parabolic Equations

166

VI.

Harnack

estimates:

the

case

p>

2

LEMMA

4.1.

There

exist a

number

u E (0,1)

depending

only

upon

N,p

and P

such

that

(4.2)

Remark

4.1.

The

location of

(x,

t)

and

the

number

'To (and

hence

R)

are

deter-

mined

only qualitatively.

However

in

view

of (4.1)

the

number u

is

quantitatively

determined

as

soon

as

P>

1

is

quantitatively

chosen.

4-(i). Expanding the positivity set

We

will

choose

the

constants

P>

1

and

C>

1

so

that

the

qualitative

largeness

of v(·, t)

in the

small

ball

BcrR(X)

turns

into

a quantitative

bound

below

over

the

full

sphere

Bl

at

some

further

time

level

C.

This

is

achieved

by

means

of

the

comparison functions of§3.

Assume

first thatpE

[2,

p(II)].

where

II

is

the

number

determined

in

Lemma

3.2,

and

consider the

function

glc,p

introduced

in

(3.3),

with

the

choices

(4.3)

1 _

k =

-(I-or)

~

2

0

'

p=uR.

At

the time level

t=C

the

support of

x-glc,p

(x,CjX,t)

is

the

ball

where

)

I(U)"¢l

'Y

=

'Y(U,II

= 2

'2

.

Choose

II

P =

A(II)

and

Since

Ixl

< 1

and

t E (-1,0]. these choices

imply

that

the

support of x -

glc,p

(x, Cj

x,

t) contains B2,

and

by

the

comparison principle

inf

v(x, C)

~

inf

glc,p

(x, Cj

x,

t)

ZeBI

{

(

·)6}~

~

2-(1+2&1) (i)

"¢l

1 -

~

p-

==

'Yo·

The

various

constants

depend

only

upon

N

and

p

and

are

'stable'

as

p'\.

2.

5. Proof of Theorem 2.2

167

Turning to the case p

~

p( 1/

),

we consider the comparison function

Bk,p

(x,

t;

x,

l)

introduced in (3.1)-(3.2), with the choice

of

the parameters k and p as in (4.3). At

t

=C

the support

of

Bk,p

(.,

C;

x,

l)

is the ball

I_

-

;;1'<

{b[~(I-

TO)--r-'

(aR)N(P-')

(C

-

i)

+

(aR)'}

= {b-yP-2

(1

- T

o

)(N-.BHp-2)

(C

-l)

+

(O'R)>-},

where

1

(0')

N

(

)P-l

-y(N,

(3)

="2

2

and

b=~

-p-

o

p-2

Choosing

(4.4)

{3=N

and

3>-

C = b-yp-2'

we see that the support

of

Bk,p

(-,

C;

x,

l)

contains

B2,

and by the comparison

principle,

(4.5)

inf

v(x,C)

~'

inf

Bk,p(X,C;x,l)

ZeBI

~

(2)-(1+'i')

Gt

{1-

Gtt'

==

-Yo·

Remark

4.2. These estimates involving the comparison function

Bk,p

hold for

all p > 2. However as

p'\.

2, the constant

-Yo

in (4.5) tends to zero. The purpose

of

introducing an auxiliary comparison function

gk,p

for p near 2 is to have the

constants under control as

p approaches the non-degenerate case p = 2.

We

also

remark that

gk,p

is a subsolution

of

(1.1) only for p close enough to 2.

5.

Proof of Theorem

2.2

Let (x

o

,

to)

E nT,

p>

0 and

(J>

0

be

fixed so that the box

Q4p((J)

is contained in

nT.

We

may assume that (x

o

,

to)

coincides with the origin and set

u.

==

u(O,O).

If

C and

-y

are the constants detennined in Theorem 2.1, we may assume that

(5.1)

Indeed otherwise

B

==

(2C);f-J ,

168

VI. Harnack estimates: the case

p>

2

and

there

is

nothing to prove.

By

Theorem

2.1

and

(5.1)

u*

~

'Yu(x,

t*),

Consider

the

'fundamental solution'

Bk,p

with pole at (0,

t*)

and

with k='Y-1U*.

By

the comparison principle, at

the

level t=(J,

we

have

~

u«,6);'

;t.;

{1-

(Sl~~I(t)t

r

(5.2)

"Ixl < p,

where

Here .\ and

b are defined

in

(2.5) and (3.2) respectively. It follows

from

(5.1) that

('Y~~2

+

1)

p>'

~

S(t)

~

('Y:-

2

+

2~

)

u~-2

(;

)

p>'.

Therefore (5.2) gives

(

pp)N!>.

u(x,(J)~u~!>'"9

'Y1,

'Y1

==

'Y1(N,p),

and

the

theorem follows with

B = max {

'Y-;>'!p;

(20)

~

} .

We

have shown that Theorem

2.1

implies the estimate of Theorem 2.2.

To

prove

the

equivalence of Proposition 2.1, assume that (2.4) holds true for all (J> 0 such

that

Q4p((J)

c n

T

.

Choose

Then if

Q4p((J)

c nT, (2.4) gives

u(xo, to)

~

2B

N

(p-2)!

>.

in(

f ) u(·,

to

+

(J).

Bp

Zo

5-(i). About the generalisations

The only tools

we

have

used

in the

proof are the

HOlder

continuity of the

so-

lutions of (1.1)

and

the

comparison principle. The integrability indicated

in

(2.7)

6.

Global

versus

local

estimates

169

guarantees the local

HOlder

continuity.(l) Moreover the comparison principle re-

mains applicable since

f

~

o.

6. Global versus local estimates

The assumption that· the cylinder Q 4p( 8)

be

contained

in

the domain

of

definition

of

the solution is essential for the Harnack estimates

of

Theorems

2.1

and 2.2 to

hold. Indeed the function

(x,

t)

-

8(x,

t)

introduced in (4.11)

of

Chap. V does

not satisfy (2.4) for

Xo

= 0 and

to

arbitrarily close to zero. This is not due to the

pointwise nature

of

(2.1) and (2.4). A Harnack inequality, with

to

arbitrarily close

to zero, fails to hold even in the averaged form (2.6).

To

see this let

1£

be

the unique

weak solution

of

the boundary value problem

(P)

{

1£t

-

(I1£

z

IP-2

1£z

)z = 0

1£(0,

t)

=

1£(1,

t) = 0

1£(,,0)

=

1£0

E C:'(O,

1)

1£o(x)

E [0,1], "Ix E (0,1)

in

Q:= (O,l)x(O,oo),

for all t

~

0,

and

1£o(x)

= 1 for x E

U,

i)·

We

claim that

(6.1)

-1

1£

1£t

>

---

-

p-2

t

in V'(Q).

Let

us

assume (6.1) for the moment. Since 0

~

1£

~

1,

by the comparison principle

(6.1) implies that

_ 1

-

(11£.IP

21£_)

<

t>

O.

• • z -

(p

- 2)t'

At any fixed level

t,

the function

x-1£(x,

t)

is majorised by

"(x

6

v(x,t)

=

~,

ti=I

Indeed

(

P-l

)

6E

-p-,l

,

(-y6)P-l

(1-

6)(p -

1)

~

~2'

p-

1

-

(Iv

z

I

P

-

2

v

z

)z

~

(p

_ 2)t and

v(O,

t) =

0,

v(l,

t) >

O.

Therefore for every 6 E (

7'

1)

there exists a constant C = C (6), such that

C(6)

1£(!,t)

~

t

1

/(p-l)'

(1) See

the

structure

conditions in

§1

of

Chap~

II, Theorem 1.1

of

Chap.

III

and

Theorem

3.1 of

Chap.

V.

170

VI.

Harnack

estimates:

the

case

p>

2

Now

assume that (2.6) holds

for

to=O, x

o

=!,

9=t

and

p=

1.

Then

for

t>I

1

~

canst

(cp!-,

+

c*)

--

0

as

t

--

00.

The proof of (6.1)

is

a particular case

of

the following

6-(i).

Regularising effects

PROPOSITION 6.1. Let u E V (0,

Ti

WJ,P(I1» be

the

unique

non-negative

weak

solution

of

(6.2)

Then

ifp>2.

(6.3)

andifI<p<2.

(6.4)

{

Ut

- div IDul

p

-

2

Du

=

0,

u(·, 0) = U

o

E

L2(11),

in

I1T'

p>

I,

U

O

~O.

-1

u

Ut>

--

-

in

1)'(11)

a.e.

t > 0,

-

p-2

t

1 u

Ut

<

--

-

in

1)'(11)

a.e.

t >

O.

-

2-p

t

PROOF:

We

only prove (6.4).

By

the

homogeneity of the p.d.e., the

unique

solu-

tion

v of (6.2)

with

initial

datum

v(·,O) = kp!-,u

o

, k > 0,

is

given

by

(x,

t)

--

v(x,

t)

= kp!-, u(x, kt).

If k

~

1,

v(·,

0)

~

U

o

and v(·,

t)

~

u(·, t)

in

11,

Vt

E

(0,

T). Fix t E

(0,

T) and let

k =

(1

+

')

for

a small positive number

h.

Then

u(x, t + h) - u(x,

t)

= u(x,

kt)

- u(x,

t)

=

k~kp!-,u(x,kt)

-

u(x,t)

=

k~v(x,t)

-

u(x,t)

~

(k~

- I)u(x, t).

By

the

mean

value theorem applied

to

( k

~

-

1),

(6.5)

h

=.!

u(x, t)

u(x,t

+ h) -

u(x,t)

~

2 _ p

(1

+e)2-li-

t

-

for

some ( e (0,

~).If

h

<0,

and

Ihl

«

I,

we

have

k <

1,

v(·,O)

~uo

and

(6.S)

holds

with

the inequality sign reversed. Divide

by

h and

in

(6.5) take

the

limit

in

'D'(I1)

as

h-+O.

7.

Global

Harnack

estimates

171

Remark

6.1. In the proof

of

the proposition, the homogeneity

of

the operator and

the positivity

of

the initial datum, are essential.

7. Global Harnack estimates

The averaged Harnack estimate (2.6) holds with

to

arbitrarily close to zero for

non-negative local solutions

of

(1.1) in the strip

ET

==

RN

X (0,

TJ,

i.e.,

(7.1)

{u

E

CI~C

(0,

T;

L~oc(RN))

n

Lr

oc

(0,

T;

Wj!:(RN))

,

Ut

-

dlV

(IDuIP-

2

Du)

= °

10

E

T

•

THEOREM

7.1. Let u be a non-negative solution

of

(7.1)

in E

T

.

There exist a

constant

B>

1 depending only upon N and p. such that

(7.2)

'V

(xo, to) E E

T

,

'V

p,

(J

> ° such that

to

+

(J

<

T,

f

u(x,

to)dx$B{

(~)~

+

r;)NIP[B!fL)

u(·,

to

+

(J)]

AlP}.

Bp(XD)

Inequality (7.2) is more general than (2.6) in that the value u(Xo,

to

+

(J)

is

replaced by the infimum

of

u over the ball

Bp(x

o

)

at the time level

to

+

(J.

In (7.1) no conditions are imposed on

x-u(x,

t) as Ixl-oo and no reference

is made to possible

initial data. The only global information is that the p.d.e. is

solved in the whole strip

ET. Nevertheless (7.2) gives some control on the solution

u as

Ixl-

00,

namely,

COROLLARY

7.1. Every non-negative solution

of

(7.1) in

ET

satisfies

(7.3)

'VxoERN,

'Vr>O,

'VeE (O,T)

UXT

B T

~

[

---.L

1

Alp

sup sup

f

~dX$

---.L 1 +

(-)

u(xo,T-e)

O<'T~T-E

p?r

P P

eP-'

r

P

Bp(XD)

PROOF:

Apply (7.2) with

to=TE

(0,

T-e),

divide by

p~

and take the supre-

mum

of

both sides for p

~

rand

T E (0, T - e).

172

VI.

Harnack

estimates:

the

case

p>

2

8. Compactly supported initial data

The proof

of

(7.2) will be a consequence

of

the following:

PROPOSITION

8.1. Let v be a non-negative solution

0/

the Cauchy problem

(8.1)

{

V

E C

(R+j

L2(RN)) n V (R+'j Wl'P(RN)) ,

Vt

-divIDvlp-

2

Dv=0

inEoo ==RNxR+,

(

)

{

E C(Br)

/orsomer

>

0,

v',O

=

Vo

~

o and _ .

RN,-B

= 0

In

r'

There exists a constant

B=B(N,p)

> 1, such that/or all

9>0,

Inequality (8.2) can be regarded as a special case

of

(7.2) when additional

infonnation

are

available on the initial datum.

Basic facts on the unique solvability

of(8.1)

are collected in §12.

We

assume

the Proposition for the moment and proceed to gather a few facts about v.

LEMMA

8.1. For each

tE

R+. the function

x-vex,

t) is compactly supported

in

RN. i.e.,

(8.3)

'fiT E

R+,

3R

=

R(T)

> 0 such that

supp{v(·,t)}

C

BR(T),

'fit E (O,T].

Moreover the 'mass' is conserved. i.e

.•

(8.4)

! vex, t) dx =

!vo(x)

dx,

'fit

~

O.

aN

Br

PROOF:

Consider the function

8k,p

introduced in (3.1)-(3.2), with p =

2r

and

(x, t)

==

(0,0). For

t=O

and Ixl

<r,

8.~.(

••

O;O.O)

~

+ -Gt} l=l

~

supvo,

Br

provided k is chosen sufficiently large. By the comparison principle, v 5

8k,p'

The

second statement follows from the first by integrating the p.d.e. over

RN x

(0,

t).

Remark

8.1

(Existence

of

solutions). In view

of

(8.3), a solution

of

the Cauchy

problem (8.1) can

be detennined by fixing any T > 0 and solving the p.d.e. in

8.

Compactly

supported

initial

data

173

the bounded domain n

T

==

B

R(T)

X (0,

T)

with homogeneous boundary data

on

Ixl = R(T) and the same initial conditions

as

in

(8.1). It follows from the

comparison principle

of

Lemma 3.1 that the solution

is

unique. This construction

and Proposition

6.1 also give the regularising inequality

(8.5)

-1

v

Vt

>

---

-p-~t'

in

V'

(Eoo)

,

and the estimate

(8.6)

supv(·,

t) $ SupVo'

RN

-

Br

COROLLARY

8.1. The quantities

(8.7)

- J

v(x,t)

IIvll

r

=

sup

p>'-!(

-2)

dx,

tER+

p?,r

P

Bp

A =

N(p

-

2)

+ p,

(8.8)

f(t)

=

sup

{7'N!~sup

IIv(.,r)lIoo,B

p

}

O<T<t

p?,r

pp!(p-2)

are finite. Moreover there exists constants

'Y.

and

'Y

depending only upon

N,p.

such that

(8.9) for all

0 < t <

'Y.

Ilv"I~-P,

andfor

all p

~

r,

pp!(p-2)

IIv(.,t)lIoo,B

p

$'Y

tN!~

Wv"I~!~,

A=N(p-2)+p.

PROOF:

The estimate (8.9)

is

the content

of

Theorem 4.5 of Chap.

V.

8-(i). Proof

of

Theorem

7.1

assuming

(8.2)

It suffices to prove (7.2) for (xo,

to)

==

(0,0) and

(J

E

(0,

T). Fix p = r > 0

and consider the Cauchy problem (8.1) with initial datum

if

x E Br,

N-

if x E R \B

r

•

By

the results

of

Chaps. III and

V,

the solution u

is

locally bounded and locally

HOlder

continuous

in

E

T

•

Therefore up to the translation that maps

(xo,

to)

into

the origin,

u(·, 0)

is

continuous

in

B

r

.

By (8.3) the comparison principle of Lemma

3.1

can be applied over the bounded domain B

R(T)

X (0,

T)

to yield v $

u.

Then

(7.2) follows from (8.2).

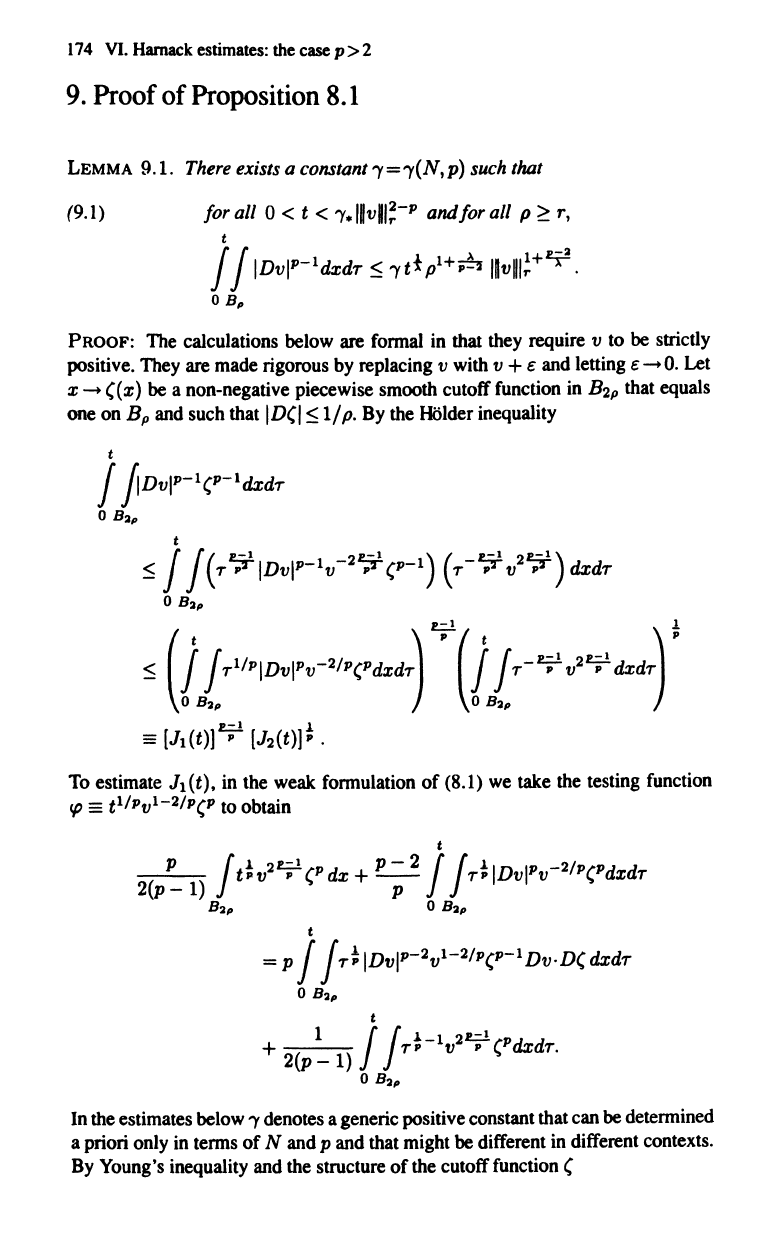
174 VI. Harnack estimates: the case

p>

2

9.

Proof of Proposition

8.1

LEMMA

9.1.

There

exists a constant 'Y='Y(N,p)

such

that

(9.1)

for all 0 < t <

'Y.llvll~-P

and for all p

~

T,

t

! ! IDvlp-1dxdT

~

'Yttp1+;!J

Ilvlll!+~.

o

B"

PROOF:

The

calculations below are fonnal

in

that they require v

to

be

strictly

positive. They

are

made rigorous

by

replacing v

with

v + e

and

lelling e

-+

O.

Let

x

-+

((x)

be

a non-negative piecewise smooth cutoff function

in

B2p

that equals

one

on

Bp

and

such that

ID(I

~

1/

p.

By

the

HOlder

inequality

t

! PDvIP-1(P-1dxdT

o Ba"

t

~!

!(T7IDvIP-IV-27(P-l)

(T-7

v2

7)dxdT

o Ba"

c!

1

~

(i

!Tl/PIDVIPV-2/P(PdXdT) P

(i

!T-Z=;V

2

Z=;dxdT)

P

o

Ba"

0

Ba"

==

[J

1

(t)]

z=;

[J2(t)]

t .

To

estimate J1(t), in the

weak

formulation of (8.1)

we

take

the

testing function

I{J

==

tl/pvl-2/p(p

to

obtain

t

p

It;

v

2

Z=;

(P

dx + P - 2 !

!Tt

IDvI

P

v-

2

/

P

(PdxdT

2(P-l)

p

Ba"

0

Ba"

t

=p!

!TtIDvIP-2vl-2/P(P-IDV.D(dxdT

o Ba"

t

+

TP-

V P (PdxdT

1

!!

1 1

2c!

2(P

-1)

.

o

Ba"

In the estimates

below

'Y

denotes a generic positive constant that

can

be

determined

a priori only

in

terms of N and p and that might

be

different

in

different contexts.

By

Young's inequality

and

the

structure of

the

cutoff function (

9.

Proof

of

Proposition

8.1

175

t

P I I

r~

IDvlp-2VI-2/p(P-l

Dv·D(dxdr

o Bap

We

conclude

that

there exists a constant

'Y='Y(P)

such that

Estimating

L

i

,

i =

1,

2,

separately

we

have

Ll

::;'Ypl+~/t

r'4!-1

(rN/>.lIv(.,

r)lIoo'Bap)(p_a~p+l)LI

v(x, r) dx) dr

\

(2p)~

p~

o h

t

::;

'Ypl+~

I

r£t!-1

[f(r)]

(p-a~Ptl)

Ilvll

r

dr

o

::;

l'

pl+~

tEf!

[f(t)]

(p-a~Ptl)

Ilvll

r

.

By

Corollary

8.1

f(t)

::;

l'

Ilvll~/'\

Therefore

for

all such

t,

Ll

::;

l'

pl+~

tf

(tlllvll~-2)

f

IIvll!+~

). 1. 1 +

E.::.!

::;

l'

pl+-;=f

tx

Ilvll

r

---x-.

::;

'Ypl+~

It

ri-1

(rN/>.IIV("

r)lIoo,Ba

p

)

~

LI

v(x, r) dx) dr

(2p)~

p~

o h

::;

l'

pl+~

t

i

Ilvlll!+~

.

On

the

other

hand

J

2

(t)

==

L2

and the

Lemma

follows.

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.