DiBenedetto E. Degenerate Parabolic Equations

106

IV.

mlder

continuity

of

solutions

of

singular parabolic equations

Ix

EKdoR

1 u(x, t) >

11-+

-

2s~+n

I

~

Ix

E

K(l-CT)doR

1 u(x, t) >

11-+

-

2s~+n

1+

I

K

doR\K(1-CT)doRI

~

Ix

E

K(l-CT)doR

1 u(x, t) >

11-+

-

2s~+n

1+

NuIKdoRI·

Therefore for all

t·

< t < 0,

Ix

EK(l-CT)doR

1 u(x,

t)

>

11-+

-

2s~+n

I

~

[(n:

lr

(/--V:/2)

+

n;p

+Nu]IKdORI.

To prove the lemma we choose U

so

small that

uN

$ i

I/~

and then n so large that

Remark

10.1. Since the number

110

is independent

of

wand

R also n is indepen-

dent

of

these parameters.

11.

The second alternative concluded

The information

of

Lemma 10.2 will be exploited to show that in a small cylinder

about

(0,0),

the solution u is strictly bounded above by

+ w

11-

- 2

m

'

for some m >

So

+

n.

In this process we also determine the number A introduced in §2 which defines the

size

of

Q

(RP,

coR). To make this quantitative let us consider the box

Q

«(3RP,

CoR)

,

(3

- I/o

-

2'

We

regard Q

«(3RP,

coR) as partitioned into sub-boxes

[(x,O)

+ Q

«(3RP,

d.R)]

where x takes finitely many points within the cube K'R.l(W) introduced at the be-

ginning

of

§ 10. For each

of

these subcylinders Lemma 10.2 holds.

LEMMA

11.1.

For every v E (0, 1) there exist a number m dependent only

upon

the data and independent

of

w and R such that for all cylinders

[(x,O)

+ Q

«(3RP,

d.R)] making

up

the partition

ofQ

«(3RP,

CoR),

meas { (x, t) E

[(x,O)

+ Q

«(3RP,

d.R)] 1 u(x, t) >

11-+

-

2:

}

< IIIQ«(3RP,d.R)

I·

11.

The

se<:ond

alternative concluded 107

PROOF:

After a translation

we

may

assume that

(x,

0)

==

(0,

0). Set

81

=

80

+ n,

and consider the energy inequality (3.8) of

Chap.

II written for (u - k)+,

where

8 =

81,81

+

1,81

+

2,

...

, m -

1,

over the cylinder Q

({J(2R)1',

2d.R). Over such a

box

(u(x, t) -

(JL+

-

;,))

+

:$;'

a.e.

(x, t) E Q

({J(2R)1',

2d.R) .

The cutoff function (x,

t)

-

(x,

t)

is

taken

to

satisfy

{

(

==

1, on Q

({JRP,

d.R),

( =

0,

on

the parabolic boundary of Q

({J(2R)1',

2d.

R) ,

ID(I

:$

d.kp,

0:$

Ct

:$

IIJ~P.

We

put these estimates

in

(3.8) of Chap. II and discard the first non-negative

term

on

the left

hand

side. This gives

(11.1)

!!ID·

(u

-

(JL+

-

;.))

+

11'

dxdr:$

(d.~)1'

(;.

)"IQ

({JR1',d.R)1

Q(fJRP

,d.

R)

+

.;

(;,y-1'

G:)"IQ

({JR1',

d.R)1

+ 'Y(d.R)N

P

(l:")

R1'

P

(l:")

•

We

estimate above the various terms on

the

right

hand

side

of

(11.1)

as

follows.

Since

8

~

81

==

80

+ n,

(

W

)2-1'

<

(~)2-1'

=

..!...

2

6

-

2

6o

+

n

d':

Therefore the

sum

of the first two terms

is

majorised

by

(d.~)1'

(;,r

IQ({JR1',d.R)

I,

for

a constant

'Y

dependent only

upon

the

data. The last

term

is majorised

by

making

use

of (3.6) of

Chap.

II and the definition (10.2)

of

d •. This gives

'Y

(d.R)N

P

(1:,,)

R1'

P

(1:,,)

:$

~pd~(~-1)

RNICIQ

({JR",

d.R) I

:$

(d.~)1'A3W-boRNICIQ({JR1',d.R)

I,

where

A3

=

2mb

o

and b

o

is

the number introduced

in

(3.6). Combining these

re-

marks

in

(11.1)

we

deduce that there exists a constant

'Y

depending only

upon

the

data and independent of w and

R,

such that

(11.2)

!!ID

(u

-

(JL+

-

;.))

+1"

dxdr:$

(d.~)1'

G:)"IQ

({JRP,d.R)I,

Q(fJRP,d.R)

lOS

IV.

Hi>lder

continuity of solutions of singular

parabolic

equations

for

all

8 = 81,81 + 1,

81

+ 2,

...

,m

-1.

apply

Lemma

2.2

of

Chap.

lover

the

cube

K

d

•

R

for

the

functions

v = u(·, t),

and

the

levels

l-

+ W

-

P.

-

2.+1'

By

virtue of

Lemma

10.2

j[U(.,

t) <

p.+

-

;.

]nKd.RI

~

(~YIKd.RI,

'tit E (-(JRP,O).

To

simplify

the

symbolism

we

set

o

A.(t)

==

{x

E

Kd.R

I u(x, t) >

p.+

-

;.}

,

A.s

= jIA.s(T)ldT.

-fjRP

Then, with

these

specifications, (2.7) of Chap. I

yields

(;')IA.s+1(t)1

~~

d.R

jIDu(x,t)ldx,

'tItE

(-(JRP,O).

A.(t)\A.+l(t)

First integrate

both

sides

in

dT

over (-{JJlP, 0),

then

take

the p-power

and

ma-

jorise

the

right

hand

side

by

making

use

of

the

IJl)lder

inequality

and

(11.2).

We

obtain

(;.

r I

A

.s+1I

P

~

'Y

(d.R)P

( i j

IDU1PdxdT)

IA.\A.+1I

P

-

1

-fjRPA.(T)

~

'Y

(;.

r

IQ

((JRP,d.R)

IIA

s

\A.+1I

P

-

1

.

From

this,

IA.+1I~

~

'YIQ({JRP,d.R) l;!t

IA.\A.+1I·

Adding

these

inequalities

for

8=81,

81

+1,81

+2,

...

, m -

I,

To

prove

the

lemma

we

have

only

to

choose m

so

large

that

(

_'Y

)~

<v.

m-

8

1 -

12. Proof of tile main proposition 109

Remark

11.1.

This estimate deteriorates

as

p

'\.

l i.e., m /

00

as p '\.1. However

the choice

of

m is 'stable'

as

p

/2.

To

proceed

we return to the box Q

(PR!',

CoR)

and recall that it is the finite

union, up

to

a set

of

measure zero,

of

mutually disjoint boxes

[(x,

0) + Q

(PR!',

d

..

R)].

Therefore Lemma 11.1 implies

COROLLARY 11.1. For every

vE

(0,

1)

there exist a number m dependent only

upon the data and independent

of

w and R such that

(11.3) meas

{(X,

t) E Q

(PR'P,

CoR)

I u(x, t) >

J.I.+

-

;.

}

<

vlQ

(PR'"

CoR)

I.

We

finally determine the size

of

the cylinder Q

(PR!',

CoR)

as

follows. First

in Corollary

11.1

select v =

Vo

and determine m accordingly. Then let

m2

be given

by

(11.4) P -

Vo

_ 2

m2

('P-

2

)

- 2 - ,

and assume,

by

taking m even larger if necessary, that m

~

m2. Then determine

A from

(11.5)

With these choices the box

Q

(PR!',

CoR)

coincides with the cylinder QR (ml,

m2)

introduced in §4. By Lemma 4.1, there exists a constant

Ao

dependent only upon

the data and independent

of

w and R such that either

or

w

bo

$

Ao

RNK.,

w

u(x t) < ,,+ -

--

, -

r-

2

m

+

1

where b

o

is the number introduced

in

(3.6).

We

summarise:

PROPOSITION

11.1. Suppose that (3.5) holdsforallcylinders

[(x,

0)

+Q

(R!',

doR)]

making

up

the

partition

ofQ

(R'P,

CoR).

There

exists a constant

Ao

dependent only

upon

the

data and indepetUknt

of

w and R such that either

(11.6)

orforaliO<p

$ R/2,

(11.7)

essosc u $

"'0

w,

where

~o

==

1 -

2-(m+l).

Q(fjpP

,cop)

12.

Proof of the main proposition

The main Proposition

2.1

now follows

by

combining the two alternatives. Set

A

==

max{Ao j AI},

."

==

min{."o

j "'l},

110

IV.

ftilder continuity

of

solutions

of

singular parabolic equations

and

let 0

be

dermed

by

.!.

=

(.!)

l/p

=

(~)

l/p

0-

4P

2

p+1'

Then

setting

Rl

==

RIO

both

alternatives

can

be

combined

into the

following

statement: either

w"o

<

ARNie

or

e880SC

u:5

'IW.

Q(pI',cop)

The

process

can

now

be

repeated

and

continued

as

indicated

in

Proposition

2.1.

Indeed,

by

Remark

2.1,

the

process

can

be

continued

as

long

as

(2.3)

holds.

12-(i). Stability for p near 2

The

proof of

the

first alternative

is

based on

the

integral inequalities (6.9)

and

(6.10). Because

of the right

hand

side of (6.9), Proposition

5.1

holds

with

constants

that deteriorate

as

p / 2.

We

briefly indicate

how

to

prove Proposition

5.1

with

constants

that

are

'stable'

as

p / 2. First,

using

the information

(5.11

)-(5.12)

we

can

show

that

there exists a positive

number

I.

such

that

meas

{(x,

t) E

Q2

I v(x, t) <

2-

1

.}

:5

lIo1Q21·

This

is

accomplished

by

the

same

technique

as

for

Lemma

12.1.

This

technique

involves constants of the

type 2

1

.(2-p).

We

may

select

p.

so close

to

2 that

2

1

.(2-p)

:5

2,

'tip.

:5

p:5

2.

With

such

a choice

the

method

can

be

carried out

as

if

the

p.d.e.

was

not

singular.

Next,

an

application of

Lemma

4.1

implies that

v(x, t)

~

2-(1.+1)

a.e.

(x, t) E

Ql.

The

application of

Lemma

4.1 over

the

box

Q2

involves

again

terms

of the

type

2

1

.(2-p).

As

remarked

before,

these

are

majorised

by

an

absolute constant

for

pE

IP.,2).

13.

Boundary regularity

The

proof of Theorems

1.2

and

1.3

regarding

the

regularity

up

to

the

lateral

bound-

ary

of

aT,

is

similar

to

the proof of

the

interior

regularity.

The

few

changes

needed

can

be

modelled

after similar modifications presented

in

§

11-13

of

Chap.

III

for

the

degenerate case p >

2.

However

the

proof of regularity

up

to

t = 0 exhibits

some

differences.

13.

Boundary regularity

III

13-(i).

Regularity

up

to

t=O

Assume that U

o

is

continuous

with

modulus of continuity

say

w

o

(·).

Fix

(x

o

,

0)

E

fl

x

{O}

and R > 0 so that

[xo

+ K

2R

] C

fl.

After a translation

we

may

assume

Xo

= 0 and construct the cylinder

Qo

(RP,

2R)

==

K2R

x

{O,

RP}.

Set

1'+

=

esssup

u,

1'-

=

essinf

u, w = essosc u.

Qo(RP,2R)

Qo(RP,2R) Qo(RP,2R)

Let

8

0

be

the smallest positive integer satisfying (3.1) and construct

the

box

Qo

(dRP,R)

==

KRX{O,dW},

(

W

)2-

P

d-

-

- 2

m

'

where the number m > 1

is

to

be

chosen. Notice that

for

all R>

0,

these

boxes

are

lying on

the

bottom

of

flT.

Also withous

loss

of generality

we

may

assume

that

2~

~

1 so that there holds

and

osc u <

w.

Qo(dRP,R) -

PROPOSITION 13.1.

There

exist constants

,."

eo

E (0,

1)

and

e,

m > 1 that

can

be

determined a priori

depending

only

upon

the

data

satisfying

the

following.

Con-

struct

the

sequences

Ro

= R,

Wo

=W

and

1

Rn

=

en

R,

wn+1

= max

{TJWni

e

R:t

} ,

n=I,2,

...

,

and

the

family

of

boxes

n=0,1,2,

....

Thenfor all

n=O,

1,2,

...

and·

essoscu~max{wni2essOSCUo}.

Q~n)

KRn

We

indicate

how

to

prove the

fIrst

iterative step of the Proposition and

show,

in the process,

how

to detennine the number

m.

Set

and consider the two inequalities

(13.1)

+ w +

I'

- 2

80

<

1'0

,

_ w _

I'

+ 2

80

>

1'0

,

So

~

2.

If

both

hold, subtracting the second

from

the

fIrst gives

112

IV.

HOlder

continuity

of

solutions

of

singular

parabolic

equations

and there is nothing to prove. Let

us

assume for example that the second of (13.1)

is

violated. Then for

alls

~

So,

the

levels

w

k

=,.,.-

+ 2

8

'

satisfy the second

of

(4.16)

of

Chap.

II.

Therefore

we

may

derive energy and log-

arithmic estimates for the truncated functions

(u - k)_. These take the

form

(13.2) sup

I(u

-

k}~(x,t)(Pdx

+ f

flD(u

- k}_(IPdxdT

O<t<dRp

J J

- -

KR

Qo(dRP,R)

~

:51'

lfiu-k}"-'D('PdxdT+'Y{jiBk,R(T}'~dT}

r ,

Qo(dRp,R)

0

(13.3) sup

IIli

2

(D;, (u -

k)_,

c)

(P(x) dx

O<t<dRP

- -

KR

:5

l'

II

Ilillliu

(D;;,

(u

-

k)_,

c) 1

2

-

P

ID(I

P

dxdT

Qo(dRP,R)

+

~

(1+In~')

{~B"R(T)lldTr(':"

,

where

Dt

and

Bt,R are defined

as

in

(4.2) and (4.4) of Chap.

II.

LEMMA

13.1. For every

vE

(0, 1), there exists a

numberm>so~

2 depending

only upon the data and independent

of

w and R such that either

(13.4)

or

where

R

p=-

2

(b

o

defined in

(3.6))

(

W

)2-

P

and

d=

2

m

•

PROOF:

Consider inequalities (13.3) written for k

=,.,.-

2":0.

As

a constant c

ap-

pearing

in the

definition of

Ili

(see (3.12) of Chap. II),

we

tak: c =

;...

Thus

we

take

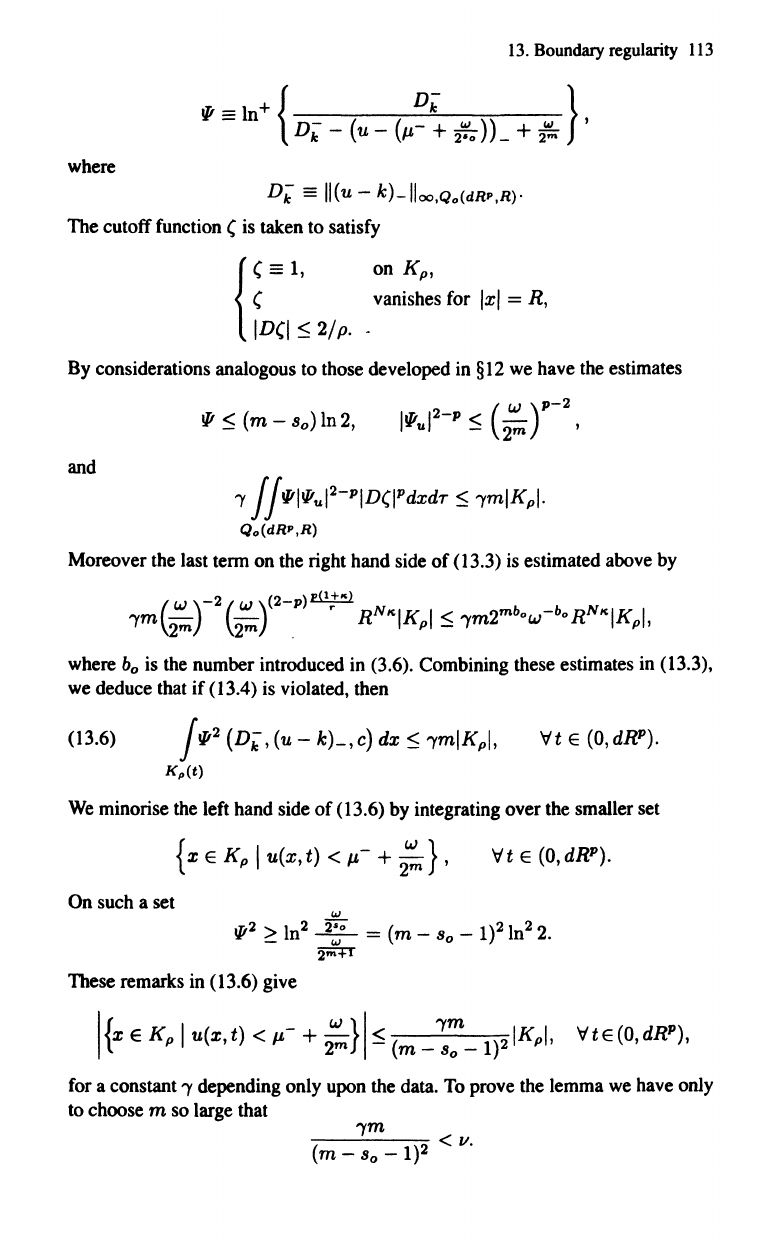
13.

Boundary

regularity

113

where

D;

==

lI(u -

k)-lIoo,Qo(dRP,R)·

The cutoff function ( is taken to satisfy

on

K

p

,

vanishes for

Ixl

=

R,

By considerations analogous to those developed in §

12

we have the estimates

and

tJi

5

(m-s

o

}ln2,

(

W

)1'-2

1

tJi.1

2

-

1'

< -

u - 2

m

'

'Y

f f

tJiltJi

uI

2

-

1'

ID(I

1'

dxdr

:5

'YmIKpl·

Qo(dRP,R)

Moreover the last

tenn

on

the right hand side

of

(13.3) is estimated above by

CW

)-2

CW

)(2-1')~

'Ym\2ffl

\2ffl

. r RNItIKpl:5

-ym2mbow-bo

RNItIKpl,

where b

o

is the number introduced in (3.6). Combining these estimates in (13.3),

we deduce that

if

(13.4) is violated, then

(13.6)

f

tJi2

(D;,

(u -

k)_,c)

dx 5 'YmIKpl,

Kp(t)

'<It

E

(0,

dRP).

We

minorise the left hand side

of

(13.6) by integrating over the smaller set

On

such a set

{ x E Kp I u(x, t) <

~-

+

2:

} ,

'<It

E

(0,

dJlP).

w

tJi2

~

In2

2:

0

= (m -

So

-

1)21n2

2.

2"'"fT

These remarks in (13.6) give

I{x

E Kp I u(x,

t)

<

~-

+

2:}1:5

(m

_:~

_I)2I

K

pl,

'<ItE(O,dR1'),

for a constant

'Y

depending only upon the data. To prove the lemma we have only

to

choose m so large that

(m -

So

-

1)2

< v.

114

IV.

HOlder

continuity of solutions of singular

parabolic

equations

Remark 13.1.

The

process described

has

a double meaning. It defines a level

IJ.

- +;:"

for

the

function u

and

the

size

of

the

box

d-

-

(

W

)2-"

- 2

m

'

within

which

the

set

where

u <

IJ.

- +;:" is small.

To

conclude

the

proof

of

Proposition 13.1, choose

II

=

11

0

,

where

110

is

the

number claimed

by

Lemma 4.1. Then

derme

m accordingly.

By

Lemma

4.1

and

inequalities (13.2)

u(x, t) > IJ.- +

2:+

1

'

V(x,t)

E

Kf

x (O,dR").

Notice that

no

shrinking occurs

in

the

t-direction. This

is

due

to

the

fact

that in

(13.1) the cutoff function, can

be

taken independent of t.

14.

Miscellaneous remarks

14-(i). Expansion

of

positivity

A crucial

fact

in

the

proof of Theorem

1.1

is

the

expansion

of

positivity of Propo-

sition

5.1.

To

focus

on this

phenomenon let

us

consider homogeneous equations

with

measurable coefficients

of

the

type

(14.1) {

V

E

L~

(0,

Tj

L~oc(!l»nLfoc

(0,

Tj

w,!;:(n»)

, 1

<p<2,

Vt - (IDvl,,-2/lij(X, t)

uZ;)Zj

= °

in

nT,

where

the

entries (x, t) -

tlij(x,

t) of

the

matrix

(aij)

are

only measurable

and

satisfy

the

ellipticity condition

for

some

A >

0.

In

such a case,

the

various costants

Ai

and

A appearing

in the

proof of Proposition 5.1

are

all zero

and

the function w introduced in (6.4)

c0-

incides

with

v.

The information (5.3)

has

been

translated into

the

dimensionless

estimate

(5.11 )-(5.12) (see

Fig.

5.2).

Let

us

think of (14.1)

as

defined

weakly

in the

cylindrical domain

K4

x

(-4",0).

The

information (5.11)-(5.12)

is

that at

the

'centre' of

K4

x (-4P,0)

there

is

a thin cylinder

KhD

x (-4P, 0)

where

v >

1.

The

conclusion of

the

argu-

ments

of

§5-9

is

that there exists a small positive

number

"Yo

that can

be

determined

a priori

only

in

terms of

N,p

and

A,

such

that

v(x,

t)

~

"Yo,

V(x,t)

E

KIX(-l,O).

14.

Miscellaneous remarks

115

Thus the 'positivity'

of

v over K ho spreads over a full cube K

1.

Actually the infor-

mation (5.11)-(5.12) is only used to apply the Poincare inequality

of

Proposition

2.1

of

Chap. I

to

derive the integral inequality (6.10). Precisely

j wf(v)(Pdx

:5

meas

{[Wk[V(X,

J]

=

O]n[(

=

I]}

jIDWk(V)IP(Pdx,

K4X{t} K4

X

{t}

for all t E (-4P, 0). Now to apply such

an

inequality it only suffices to have the

information

meas{[Wk[v(X,t)] =

0]nK2}~Qo

>

0,

for some Q

o

> 0,

Vt

E

(-4

P

,

0).

In particular it is not necessary to know that the set

[Wk(V)

=

0]

==

[v

~

1]

is con-

centrated

in

a cylinder about the origin. We summarise:

THEOREM

14.1. Let v

be

a non-negative

weak

solution

of(14.1)

in

the

cylin-

drical

domain

Q4(46)==K

4

x (O,46)for

some

6>0.

Assume

moreover

that

meas{x E

K21

v(x,t)

> k

o

}

~

Qo,

for

some

positive

numbers

ko and Q

o

and all t E (26,46).

Then

there

exists

a

number

'Yo

="10

(N,p, A,

6,

Qo,

k

o

)

that

can

be

determined a priori

only

in

terms

of

the

indicated quantities,

such

that

v(x,

t)

~

'Yo,

V (x, t) E

Kl

x (36,46).

14-(;;). Extinction in finite time

Weak solutions

of

(14.1) may become extinct in finite time. We refer to §2-3

of

Chap.

VII

for a precise description

of

this phenomenon. The extinction profile is

the set

a

[v

=

O)"'\aT.

Theorem 14.1 implies that the extinction profile is a portion

of

a hyperplane normal

to

the

t-axis.

Indeed

if

u(xo,

to)

>0

for some

(xo,

to)

E n

T

•

by continuity we may construct a box about

(xo,

to)

where the assumptions

of

Theorem 14.1

are

verified.

It

follows that the positivity

of

vat

(xo,

to)

expands at

the same time

to

to the whole domain

of

definition

of

v(·,

to).

14-(iii). Continuous dependence on the operator

We only remark that the comments

on

stability made

in

§14

of

Chap. III. in the

context

of

degenerate equations. carry

over

with

no

change

to

the case

of

singular

equations.

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.