DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.

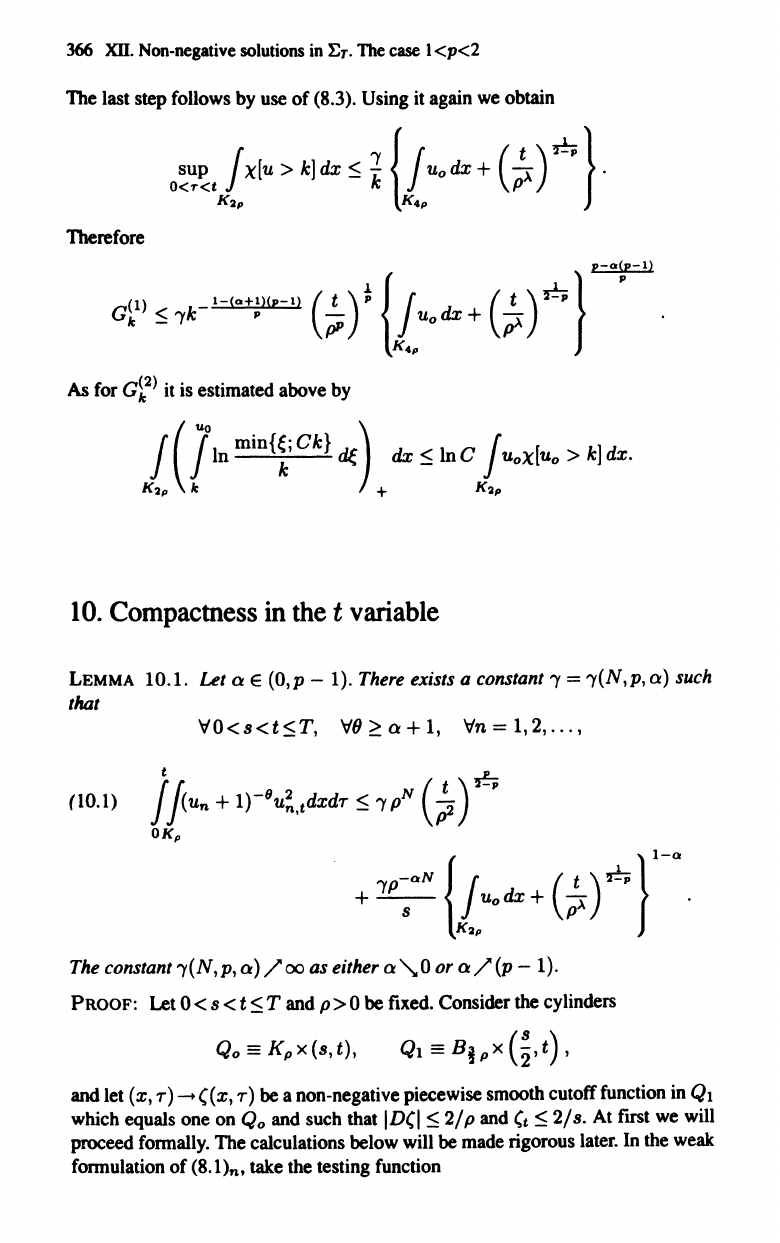
366
XII.
Non-negative
solutions
in
1::,.
The
case
1 <p<2
The last step follows by
use
of
(8.3). Using it again
we
obtain
1berefore
As for
G~2)
it
is estimated above by
10.
Compactness in the t variable
LEMMA
10.1. Let 0 E
(O,p
- 1).
There
exists a constant
'Y
= 'Y(N,p,o)
such
that
VO<s<t$T,
V8~o+1,
Vn=1,2,
...
,
'YP-aN
{f
( t
)~}l-Q
+--
uodx+-X
s P
K2p
The
constant 'Y(N,p,
0)
/00
as
either 0
'\.0
or
o/(p
-
1).
PROOF:
Let 0 < s < t $ T and
p>
0 be fixed. Consider the cylinders
QoEKpx(s,t),
QIEBtPx(i,t),
and
let (x,
T)
-+
( x,
T)
be
a non-negative piecewise smooth cutoff function in
Ql
which equals one on Qo and such that
ID(I
$
2/
p and
(t
$
2/
s.
At
first
we
will
proceed formally. The calculations below will
be
made rigorous later.
In
the weak
formulation of
(8.1
)n,
take the testing function
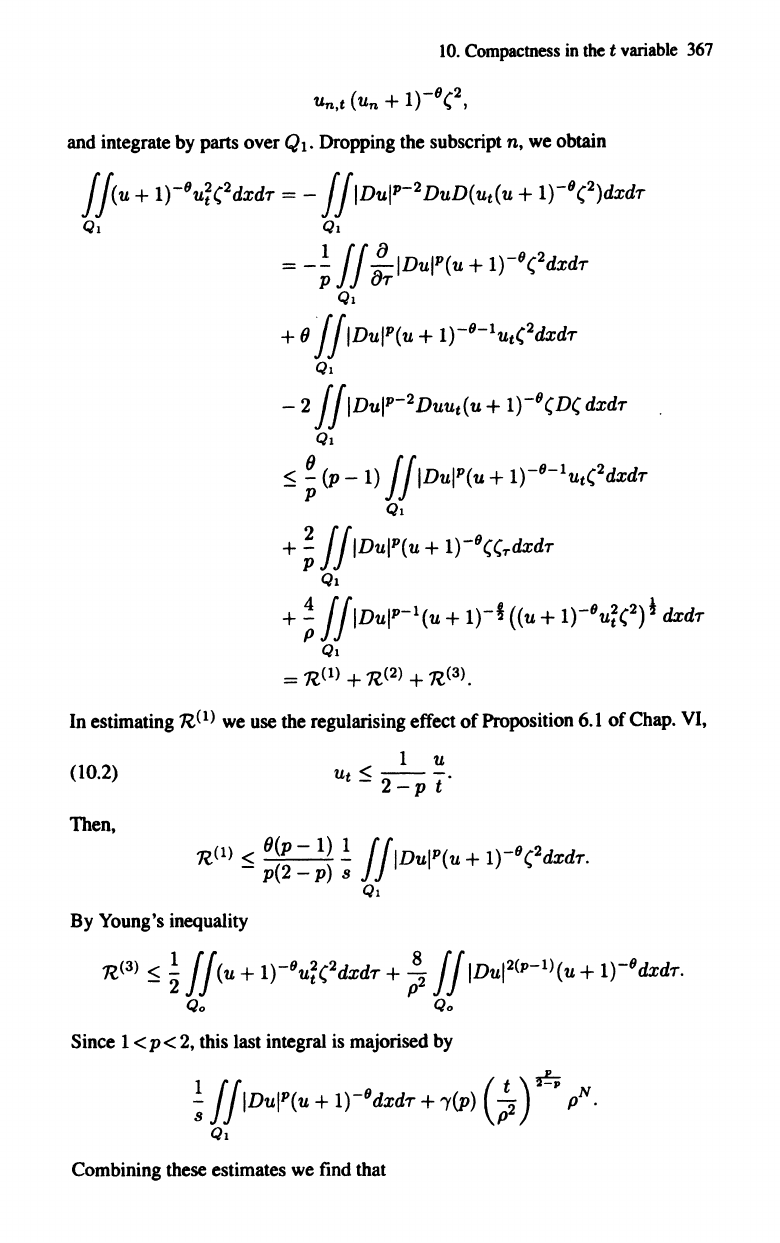
10.
Compactness
in
the
t variable
367
Un,t (un + 1)-8(2,
and integrate by parts over
Ql.
Dropping the subscript
n,
we obtain
II{u+
1)-8u~(2dxdr
= -
IIIDu
IP
-
2
DUD{U
t
(U+ 1)-8(2)dxdT
Ql Ql
=
-t
II
!IDuIP(u
+
1)-8(2dxdr
Ql
+
(J
f
IIDuIP(u
+ 1)-8-1
Ut
(2dxdT
Ql
- 2
IIIDu
IP
-
2
Duut{u
+
1)-8(D(
dxdr
Ql
~
~
(p-1)
IIIDuIP(u+
1)-8-1
Ut
(2dxdr
Ql
+
~
IIIDuIP(U
+
1)-8((Tdxdr
Ql
+
~
IIIDuIP-1{u
+
1)-1
({u +
1)-8u~(2)
1
dxdr
Ql
=
n(l)
+
nP)
+
n(3).
In
estimating n (
1
)
we use the regularising effect
of
Proposition 6.1
of
Chap. VI,
(10.2)
Then,
1 u
Ut
<
---.
-
2-p
t
By Young's inequality
n(3)
~
~
II{u
+
1)-8u~(2dxdT
+ ;
II
IDuI
2
(p-l){U
+ 1)-8dxdr.
Qo Qo
Since 1 < p < 2, this last integral is majorised by
Combining these estimates we find that

368 XII. Non-negative solutions in
I:T.
The case
1<p<2
By
(8.5),
if
aE
(O,p
-
I),
this is estimated by
; ffiDuIPu-(O+I)(U + 1)-[8-(o+l)ldxdr
Ql
~
"Y(a,~)pON
JJIDUp-~-a
IPdxdr
Ql
"Y(a,p)
{J
(~).,!p}
1-0
~
uodx+
~
,
s P
K2p
and the lemma follows by fonnal calculations. The calculations
are
fonnal since
'Un,t
(un
+
1)
-8
(2,
need not be an admissible testing functions in (8.1)n. The ar-
guments would be rigorous
if
(10.3)
Indeed,
if
so, we may take in the weak fonnulation (8.1)n the testing function
'Un(t
+
h)
- un(t) ( 1)-8/"2
h u
n
+
..
,
hE(O,T-ls),
ls~t<T-h.
The limit
as
h
-t
° is justified and we may proceed
as
before.
lO-(i). Approximating estimates
Therefore to prove the lemma it suffices
to
establish (10.1) for a sequence
of
approximating solutions satisfying (10.3). The unique solution
of
(8.l)n,
can be
approximated by the solutions
of
(10.4)
{
vn,;
E C
(0,
T;
L2
(B;»)nV
(0,
T; W!'p (B;)) ,
j = n +
1,
n + 2,
...
,
!rVn,j -
div
(I
DVn,j
IP-2
DVn,j) = ° in B
j
x
(0,
T),
Vn,j(·,t)
11%I=j=
0, Vn,j(·,O) =
Uo,n,j,
where B; is the ball
of
radius j about the origin
and
{uo,n,j }
;:n+l'
is a sequence
offunctions
in
C':'
(Bn+l), such that .
Uo,n,j
--+
uo,n in
L~oc
(Bn+t>
,
and

10.
Compactness
in
the
t
¥ariable
369
/Uo,n,jdX
~
2/u
o
dX
Vp
>
o.
Kp Kp
As indicated in § 12
of
Chap. VI.
8 8
Vn,j,
-8
Vn,j
--
Un,
-8
Un,
in
C1!c
(ET)
Xl Xl
Vl=
1,2,
...
,N,
for some Q E
(0,1).
The unique solvability
of
(10.4) can be established by a
Galerlcin procedure. Such a method also yields
To establish (10.1) for
Vn,j
is suffices
to
show that
(10.6)
ID!
Vn,jl
E
L?oc
(B
j
).
In
the remarks below we drop the subscript n, j and write v =
Vn,j.
We
write
(10.4) for the time levels t+h and t and set
w = vet +
h~
- vet) ,
hE
(0, T -
!s),
!s
~
t < T - h.
By difference
(10.7)
where
Jh
= IDv(t +
hW-
2
Dv(t + h)
-IDv(t)I
P
-
2
Dv(t).
In the weak formulation
of
(10.7) take the testing function w
(t-
V+
which van-
ishes on
Ixi
= j and for t
~
~.
This gives
T-h
T-h
t+h
(10.8) /
/(t
- i) + A
o
,jlDwl
2
dxdr
~
'Y
/
/1
:r
f vex,
r)drr
dxdr,
where
!
Bj
0 B
j
t
1
Ao,j =
/ID(svn,j(t
+
h)
+
(1
- s)v
n
,j(t))IP-
2
ds.
o
If
/C
is a compact subset
of
B
j
x
(s,
T).
we have
Ao,j
~
'YIIDvn,j
lI~i
.
It follows from (10.8) that
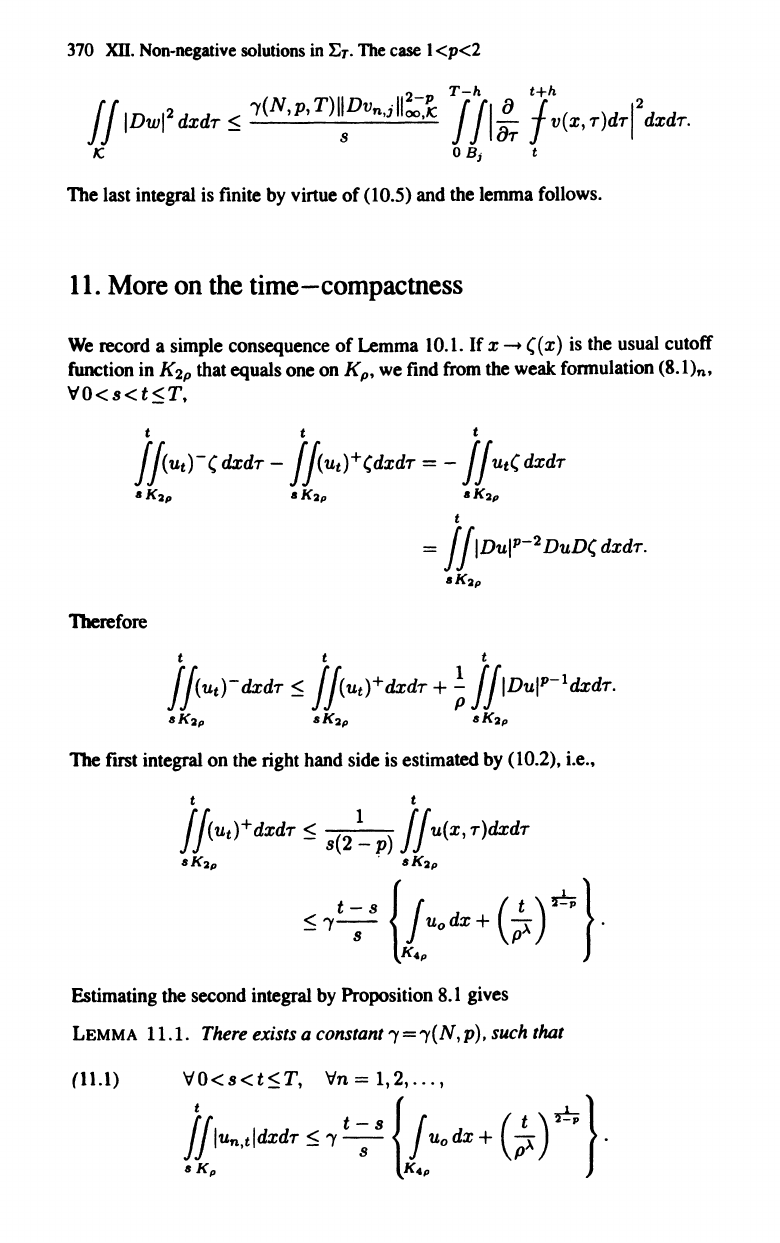
370
XU.
Non-negative
solutions
in
1::1.
The
case
I
<p<2
The last integral
is
finite
by
virtue of (10.5) and the lemma follows.
11.
More on the time-compactness
We
record a simple consequence
of
Lemma 10.1. If x -
((x)
is
the usual cutoff
function in
K
2p
that equals one on Kp.
we
find
from
the weak fonnulation (8.1)n.
VO<s<t$T.
t t t
ffiUt)-(dxdT
- ffiUt)+(dXdT = -
ffUt(dxdT
aK2p
aK2p aK2p
t
= f
f1Du1JI-2
DuD(
dxdT.
aK2p
1berefore
The fust integral on the right hand side
is
estimated
by
(10.2). i.e
.•
t-s{f
(t),!p}
$
'Y-
s
-
uodx
+
p>'
•
K4p
Estimating the second integral
by
Proposition
8.1
gives
LEMMA
11.1.
There
exists a constant
'Y
=
'Y(
N, p),
such
that
(l1.1)
VO<s<t$T,
Vn
=
1,2,
...
,
if
t-s{f
(t)¢P}
!{~un.tldXdT
$
'Y
-s-
K4puodx
+
p>'
•

12.
The limiting
process
371
12.
The
limiting process
By construction
Un
/,1.£
a.e. in
ET
and by (S.3)
for all
0<
t
~
T. Moreover by (11.1)
(12.2)
p-l-
..
By Lemma
S.l
the sequence
{'Un
J>
} is equibounded in
LP
(0, Ti W1,P(K
p
»)
,
Vp
> 0, provided 0 E
(O,p
-1).
Since the whole sequence
{unhJEN
-1.£
in Lloc(RN),
p-l-..
p-l-
..
Un
J>
--+
1.£
J>
weakly in
LP(O,
Ti W1,P(K
p
»,
Vp
> 0.
This implies that the sequences
Un,A:
=
Un
1\
k = min{un,k}
are equibounded in
LP
(0,
Ti W1,P(K
p
»)
, Vp>O, and
(12.3)
Un,k
--+
1.£
1\
k weakly in
LP
(0, Ti W1,P(K
p
»)
,
Vp>
0,
Vk
>
0.
LEMMA
12.1.
DUn,A:
-
DUA:
strongly
in
Lfoc(ET).
PROOF:
In the weak fonnulation
of
(S.1)n, take the testing function
to obtain
(12.4) jjIDUn,A:IPcpdxdT = jjIDUnIP-2DUn.DUkCPdxdT
ET ET
+
jjlDunlP-2
D(u +
v)(UA:
- Un,k)DcpdxdT
ET
+ j j
Un,t
(Uk
-
Un,k)cpd.xdr
==
10
+
It
+ 12.
ET
We first estimate the integrals Ii, i = 1, 2. Let 0 E (0, p - 1) be so small that
(0 +
1)(P
-
1)
~
1.
Then by Lemma
S.l
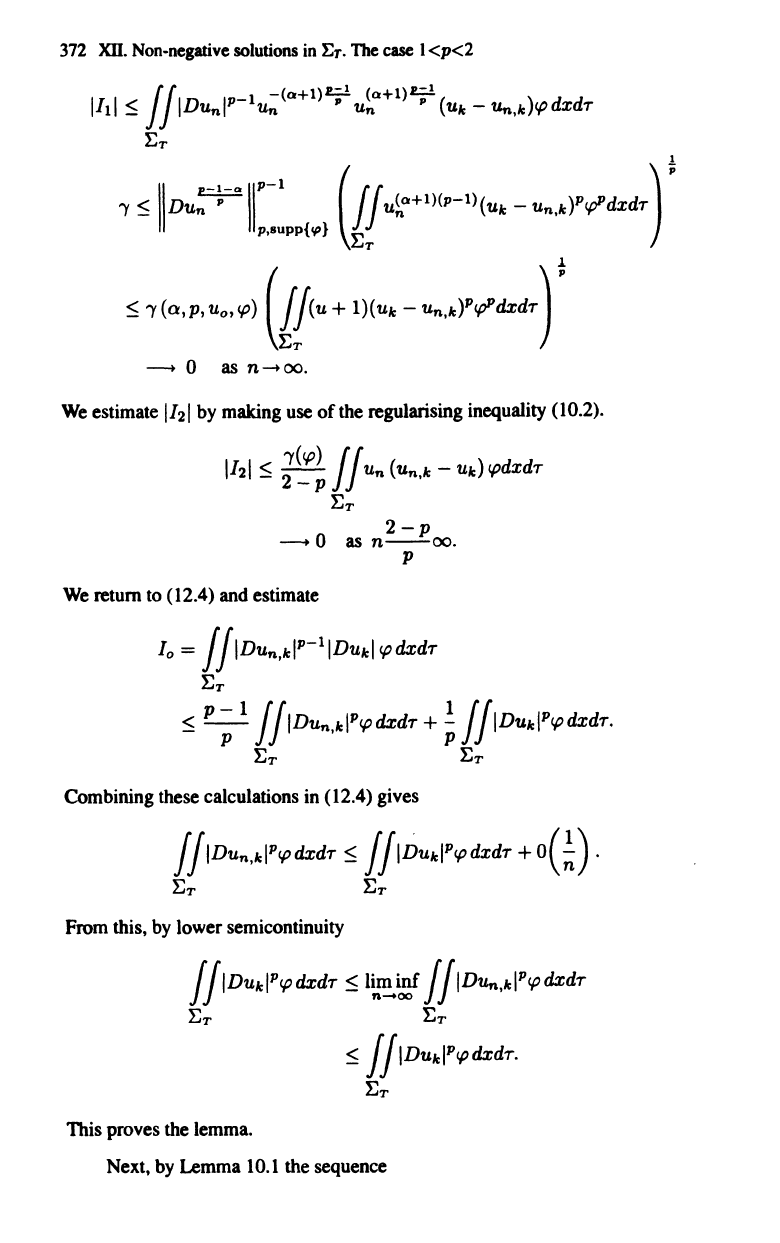
372
XU.
Non-negative solutions in
l:r.
The case I
<p<2
I
I
I
<
j
r
riD
11'-1
-(01+1)7
(01+1)7 ( )
dxd
1 _ J
Un Un
Un
Uk
-
Un.k
I{)
T
ET
1
I'
~
IIDu:-~-"IIP-1
(I
I
u~+1)(P-1)(Uk
-
un.k)Pl{J"dXdT)
P
P.8Upp{.,}
ET
.1
,;;
~(Q,P'U.,<p)
(j[<u+
l)(u.
-Un,,)P<p"dxdT) ,
--+
0
as
n
.....
oo.
We
estimate
1/21
by
making
use
of
the
regularising inequality (10.2).
1/21
~
;~~
If
Un
(Un.k
-
Uk)
I{)dXdT
ET
2-p
--+
0
as
n--oo.
p
We
return
to
(12.4)
and
estimate
10
=
IIIDun.klp-1IDUkll{)
dxdT
ET
~
p;
1
IIIDUn.kIPl{)dxdT
+
~
IfIDUkIPl{)dxdT.
ET ET
Combining these calculations
in
(12.4) gives
From
this.
by
lower semicontinuity
IIIDUklPl{)dxdT
~
l~~~
IIIDUn.kIPl{)dxdT
ET
ET
~
IIIDUkIPl{)dxdT.
ET
This proves the
lemma.
Next,
by
Lemma
10.1
the sequence

12.
The
limiting
process
373
{
a
2-.}
at
(Un
+
1)2"
nEN
is equibounded in
L~oAET)
for all
(J~
0:
+ 1 and for all o:E
(O,p
- 1). Therefore
a 2-' a 2-'
2{
2 )
at
(Un
+
1)2"
-+
at
(u +
1)"'-
weakly
in
L s,
t;
L (Kp) ,
for all 0 < s < t
:5
T and all
p>
O.
This implies that
{
:t
Uk,n}
E
L~ocET
unifonnly in n and
(12.5)
o
Choose
1/J
EXloc
(ET) and in (S.I)n consider the testing function
r.p=
(1/J
- u)+.
Fix O<s<t:5T and let
Then
o
(1/J
- u)+ =
(1/J
-
U"
k)+
EXloc
(ET),
so
that
r.p
is an admissible testing function. It gives
t
(12.6)
!!{
!U
n
(1/J
- u)+ + IDu
n
I
P
-
2
Du
n
·D(1/J
-
U)+}
dxdr =
O.
SRN
Since
Un
:5
u,
Vn
EN,
we have
Therefore in view
of
(12.5)
t t
n~!!
:r
u
n
(1/J
- u)+dxdr = !
j<u"
kh(1/J
-
u"
k)+dxdr
SRN
sRN
t
==
!
!u
t
(1/J
- u)+dxdr.
SRN
Analogously,

374
XII.
Non-negative
solutions
in
l::r.
The
case
1 <p<2
IDu
n
l
p
-
2
Du
n
D('I/1
-
u)+
= ID(Un "
k)IP-2
D(u
n
"k)D('I/1 -
U"
k)+
=
(IDu
n
.kI
P
-
2
DUn.k
-IDuklp-2
DUk)
.D('I/1
-
Uk)
+ IDuI
P
-
2
Du·D('I/1 - u)+.
By
a calculation similar
to
that in Lemma 5.2 and leading to (5.6) we have
Therefore taking into account Lemma
12.1 and letting
n-+oo
in (12.6) gives
t
j j
{Ut('I/1
-
u)+
+ IDulp-2
Du·D
('1/1
- u)+} dxdr =
0,
·a
N
o
for all
'1/1
EX
loc
(ET)' It remains
to
prove that U takes the initial datum U
o
in the
sense
of
Lloc(RN) and that
ueS·.
12-(i). Continuity
in
Lloc(RN) at t=O
Fix p > 0 and let u
o
•
e
be
a net
of
functions satisfying
{
uo.e
==
0,
u
o
•
e
--+
u
o
,
for Ixl > 4p
in
L1
(K
2p
)'
Such a family
can
be
constructed
by
fllSt defining a function that coincides with
U
o
in K
3p
and zero otherwise and then
by
mollifying the function so obtained.
Let also
U
e
be
the unique solution
of
(1.1) with initial datum u
o
•
e
•
We take the
difference
of
(8.I)n
and the equation satisfied by
Ue.
In the p.d.e.
so
obtained take
the testing function
tp =
[(un
- u
e
)+
+
6l
a
(
where
(1,6
e (0,1) and
x-«x)
is the usual cutoff function in K
2p
that equals one
on
Kp.
We perfonn an integration by parts and let
6-+0,
8-0,
(1-0.
to
obtain
j(Un(t) - ue(t»+dx
~
j(Uo.n - uo.e)+dx
Kp
K2p
t
+
2;
j j (IDunIP-1 + IDueIP-1) dxdr.
OK2p
We use (8.4), interchange the role
of
Un
and
Ue
and, for t > 0 fixed, let n -+
00.
This gives

12.
The
limiting
process
375
jIU(t)
- ult(t)ldx $ j
Iu
o
-
uo,ltl
dx
Kp
K2p
From this
jlu(t) -
uoldx
$ 2 j
Iu
o
-
uo,ltldx
+
jlult(t)
-
uo,ltldx
+ O(t;) .
Kp
K2p
Kp
Letting t
'\.
0
lim-suPt'\.o jlu(t) -
uo)ldx
$ 2 j
Iu
o
-
Uo,ltldx,
'VeE(O,
1).
Kp
K2p
12-(ii).
UES·
By
(10.2).
'Vn
E N
and
for
all k > 0
o(
) 1
Un
- U
I\k
<
---.
at
n -
2-p
t
As
n-+oo
1 U
(u 1\
k}t
$
--
-
a.e.
in
ET.
2-pt
(12.7)
The
limit
is
flISt
taken
in
1)'(0,
T)
and
then
(12.7)
holds
almost
everywhere
in
ET
in
view
of
(12.5).
Next
from
Lemma
9.1
it
follows
that
'VC> 1
t
jjlDUnlP
~
X[k
<
unlx[u
<
CkldxdT
=
O(~).
sKp
Here
we
have
used
the
fact
that
Un
/ U implies
[un
<
Ckl
~
Iu
<
Ckl.
Letting
n
-+
00
for
k > 0
and
C>
1
fixed
yields
by
lower semicontinuity
t
jjIDuIP~X[k<U<CkldxdT
= 0
(~).
sKp
We
conclude
by
remarking that
the
requirement u E
S·
is
necessary
and
sufficient
for
uniqueness.
Indeed. if solutions
in
S
are
unique.
they
can
be constructed start-
ing
from their traces on t = T E (0, T)
to
yield u E
S·.
Vice
versa solutions
in
S·
are
unique.
