DiBenedetto E. Degenerate Parabolic Equations

346

XII.

Non-negative solutions

in

ET.

The

case 1

<p<2

Suppose now that there exist another subnet, indexed with {r"} and a Radon mea-

sure

jJ.,

such that

We

will prove that

J.I.

==

jJ..

Let u E

(0,1)

and write (2.8) with

1/J

==

1 and ( the

standard cutoff function in

K(l+u)p.

Letting k

-+

00,

standard calculations give

VO<s<tST

t

(4.4)

jU(S)dXS

j

u(t)dx+

:pjjIDuIP-1dxdr.

Kp

K(1+")p

BK2p

We

estimate the last

tenn

by using (4.2) and let s

'\.

0 along

r'

while

t>

0 remains

fixed. Then we let

t

'\.

0 along the net

r"

to

get

Since

uE

(0;1)

is arbitrary, interchanging the role

of

J.I.

and

jJ.

proves the theorem.

5.

The

uniqueness theorem

Let

S·

denote the subclass

of

S

of

those non-negative local weak solutions

of

(1.1)

in

ET, satisfying

(5.1)

for some

"'(

= ",((N,p, t),

Vk

E

R+,

(5.2)

lim

fr

f

IDuI

P

.!.

dxdr = 0,

k-oo

J u

K:n[k<u<Ck]

for every compact subset

K:.

C

ET

and for all

C>

1.

In section §§8-12 we will

construct solutions

of

the Cauchy problem (1.1)-(1.2) that satisfy both (5.1) and

(5.2); therefore

S·

is not empty. Corollary 3.2 suggests that (5.2) is almost satisfied

s.

The

uniqueness

theorem

347

by all solutions in

S.

It would

be

of

interest to know whether the inclusion

S*

c S

is

strict. .

THEOREM

5.1. Let

Ul.

U2 E S* satisfy

5-(i). Preliminaries

LEMMA

5.1.

LetuEs*.

Then/oraIlO<s<t'5,T,

Vp>O,

VC>

1,

t

lim

ff1ut/x[k<u<CkJ

dxdr

=

O.

1c-oojj

BKp

PROOF:

Consider (2.8) written for

Uk

replaced by

UCk.

against testing functions

7J

= ( In

(k/

2w

k,C)

where

x-(x)

is

the standard cutoff function in

K2p.

and

{

!k,

Wk,C

==

u,

Ck,

o

'5,

u

'5,

!k

< u <

Ck

u~Ck.

It follows from these definitions that

7J

'5,

0 a.e. in ET and

7J

= 0 a.e.

on

the set

[O<u'5, !kJ.

By

calculation from (2.8) we obtain

t t

(5.3)

II!

uC1c7Jdxdr

'5,

IIIDU1P;X(k/2<u<CkJdxdr

SK2p

t

+In2C

IIIDUCkIJl-IX(U > k/211D(ldxdr.

BK2p

The

fll'St

integral on the right hand side

of

(5.3) tends to zero

as

k -

00

by

virtue

of

(5.2).

We

estimate the second integral. formally.

by

348

XII.

Non-negative solutions in

~T.

The

case I

<p<2

t

In2C

ff

-p-}}

IDuCkI

P

-

1

x[u

>

k/2]

dxdr

sK

lp

t

In

2C

ljlD

IP-l

-

(<>+I)(p-l)

[ k/2]dxd

=--

UCk

1.£

pUP

Xu>

r

p ,

SK2p

cl

~

In

;c

(p

_

~

_

0)

p-l

(if

,DUcr

1PdXdr)

P

SK2p

1

X

(if

u(O+1)(P-l)X[U

> k/2]dxdr) P

SK2p

If

we

choose 0 E (O,p - 1) so small that (0 +

l)(p

- 1)

~

1, the estimate is

rigorous and the last

tenn

in the right hand side

of

(5.3) tends to

zero

as k

-+

00,

since

1.£

E

LJoc(ET)'

These remarks in (5.3) give

t

ffUt

ln

(2~,c)

(X[Ut

< O]X[(k/2)<u<Ck] dxdr

SK2p

t

~

ff

Uti

In

2W:,c

I

(X[Ut

~

O)X[u

>

k/2]

dxdr + 0

(~)

.

SK2p

In

view

of

the definition

of

Wk,C

this gives in turn

t t

ff1ut\X[k

<1.£<

Ck]dxdr

~

'YffUtX[Ut >

O]X[u

> k/2]dxdr+O

(~).

SKl

p

SK2p

1be last integral is estimated by means

of

(5.1) and the lemma follows.

Remark

5.1.

The

assertion

of

the lemma is trivial

if

Ut

E

LJoc(ET)'

We

give next a weak fonnulation for the difference

of

two solutions

1.£1,1.£2.

First we recall that, by Lemma 2.3, the truncated function

ifO<U2<k

if

u2~k

is

a distributional supersolution

of

(1.1),

'Vk

>

O.

We

write (2.8) for

U2,k

against

the testing functions

S.

The

uniqueness

rheorem

349

where (

is

a non-negative piecewise smooth cutoff function in K( 1+(7)p,

0'

E

(0,

1),

such that

(5.4)

(

==

1 on

Kp

and ID(I:5

1/O'p.

In

view

of the definition of X

10c

(ET) and

the

regularity properties (2.1) of

Ui,

i =

1,

2,

such a choice

of

testing function

is

admissible, modulo a density argument.

On

the other hand the weak formulation (2.7) of

Ul

holds against

the

same

testing

functions. Therefore setting

kER+,

we

obtain

by

difference the

weak

formulation

t

(5.5) / /

{!

W(k)(1/J

-

ulh(P

+ J

k

D(1/J

-

Uil+("}

dxdr

SK(l+a)p

t

:5

-p

/ /Jk(1/J -

ud+(,,-l

D(dxdr

\:/1/J

E Xloc(E

T

),

sK(l+a)p

where

Jk

==

IDull,,-2Dul -IDu2,klp-2Du2,k

Set also

1 .

= /

~

{ID

(~Ul

+

(1

-

~)U2,k)IP-2

D

(~Ul

+

(1

-

~)U2,k)

} d{

o

~

(iID({Ul

+

(1

-O

....

)IP-'d{)

Ow(')

1

+

(p

-

2)

(

/ID(~Ul

+

(1

-

~)U2,k)IP-4

o

XD(~Ul

+

(1

-

~)U2,k)(~Ul

+

(1-

~)U2,k)z;d{

)W(k),Zj'

1

Ao

==

/ID(f.Ul +

(1

- f.)U2,k)I,,-2d{.

o

LEMMA

5.2.

Ao:5"~1IDw(k)IP-2.

PROOF:

If

IDu2,kl

~

IDw(k)l,

we

have

350

xu.

Non-negative

solutions

in Er. The

case

I <p<2

1berefore

ID(eUI +

(1

-

e)u2,A:)1

= IDu2,k +

eDW(k)

I

~

IID

u

2,kl-

eIDW(k)11

~

(1

- e)IDw(k)

I.

A. $

(/<1

-

(~'d{)

IDw(.r'

=

~IIDW(k)IP-2.

p-

where

eo

E (0,1)

is

defmed

by

_ I

Du

2,kl

( )

eo

=

ID

leo,

1 .

W(k)

From

the definitions set

forth

and

Lemma

5.2

we

have

(5.6)

{

JkDw(k)

~

(p - I)AoIDw(k)

12

,

IJkl S

AoIDW(k)1

S

p~IIDW(k)IP-I.

In

what

follows

we

will

use

these inequalities without specific

mention.

6.

An auxiliary proposition

PROPOSITION

6.1.

Let

Ui

E

S·

, i =

1,

2, satisfy

wet)

==

(UI -

U2)(t)

- 0

in

Lloc(RN)

as

t -

O.

6.

An auxiliary proposition

3S

I

Then W E

Loo

(0, Tj Lfoc(R

N

»)

,

Vq

E [1,00). Moreover

Vq

~

1 there exists a

constant ",(=",(N,p, q), such that

t

(6.1)

jlw(tWdX

~

(0';)"

j jlwl9+(,,-2)dxdT,

Kp

OK(1+O')p

for

all

p>Oandforall

O'E

(0,1).

The proof

is

based on

an

iteration procedure and uses recursive inequalities

obtained

from (5.5) with suitable choices

of

testing functions

1/1.

6-(;). Testingfunctions in (5.5)

For h>O, set

(6.2)

W/i).h"

(UI -

",

••

)t

-

{:/i)

and

in

(5.5) consider the testing function

ifW(k)

~O

ifw(k) < h

ifw(k)

~

h

(6.3)

1/1

==

Ul,l/r: +

~

(w(t),n

+

e)

a

(w(t),m

+

e)

b E X'oc(E

T

),

where

eE(O,I),

a,b>O,

n,mENj

n>m+1.

We

obtain

(6.4) j

W(k)

(1/1

-

ul)+("dx

- j

W(k)(1/1

-

ud+("dx

RNX{t}

RNX{B}

t t

-

jjW(k)!(1/1-ud+("dxdT+

jjJ

k

D(1/1-

u

d+("dXdT

BRN

t

::;

-p

j

jJ

k

(1/1

-

Ud+(,,-l

D(dxdT.

BRN

In

using

1/1

as

a testing function in (6.4)

we

keep in

mind

that the truncated functions

Ui,h,

i = 1,2,

Vh

>

0,

are regular in the sense of (2.1).

In

particular the first

two

integrals

on

the left hand side

of

(6:4) are well defined V 0 < 8 < t

~

T.

We

will

eliminate the parameters

e,k,8,n,m

by

letting

e-O,

k-oo,

8-0,

n,m-oo

in

the indicated order.

352 XII. Non-negative solutions in

I:r.

The case I <p<2

6-(U). The limit

as

E-+O

We

multiply both sides

of

(6.4) by E and let E

-+

0, while k,

8,

n,

m remain

fixed. From the definition

(6.3)

of

t/J

it follows that

\;IrE

(0,

T]

the net

[W(k)(Et/J-

Eud+]("

r), is equiboundt:d in Lloc(RN). Moreover it converges to

[W(k)

(w~).nf

(w~).m)

b]

(.,

r)

a.e. K

2p

,

and it is majorised a.e. in RN by

W(k)

(w~).n

+

If

(w~).m

+

I)b

(·,r) E Ltoc(RN).

1berefore for all 0 < r

~

T, as E

-+

0

(6.5) f

W(k)(t/J

-

ud+(?dx

-+

f

W(k)

(w~).nf

(w~).m)b

(Pdx.

RNx{r} RNx{r}

This determines the limit for the first two terms

on

the left hand side

of

(6.4). To

examine the remaining terms we let

'iii, i = 1, 2,

be

arbitrarily selected but fixed

representatives

out

of

the equivalence classes

Ui,

define

iii,

iii(k)

accordingly, and

let

LE

==

-E

f f

W(k)

:r

(t/J

- ud+(Pdxdr

sRN

t

=

-a

f f

w~).n

(w~).n

+Er-

1

(W~).m

+E)b!

w~).n(PX(gE)dxdr

SRN

t

-b

f f

w~).m(w~).n

+Er(W~).m

+E)b-l

!

w~).m(PX(gE)dxdr

sRN

t

-f f

w(k)(1

- EUlhx(FE)(Pdxdr

BRN

==

L~l)

+

L~2)

+

L~3)

.

We claim that

L~3)

- 0 as E

-+

O.

Indeed

6.

An auxiliary

proposition

353

t

IL~3)1::;

JJeIW(k)II!UIIX(Fe)dxdr.

aK2p

On the set

Fe

we

have

1 1 1

a+b

'Y

- ::;

Ul

::; - +

-(n

+

1)

==

-,

e e e e

eIW(k)/

::;

'Y

a.e.

Fe·

Therefore

(6.6)

and the assertion follows from Lemma 5.1.

Since

k, n, m

are

fixed, the integrands in

L~i)

• i =

1,

2,

are

in Lloc(ET) uni-

fonnly in

e.

Moreover they have a.e. limits that

are

in Lloc(ET) and their abso-

lute value

is

majorised almost everywhere in ET, unifonnly in

e,

by functions

in

Ltoc(ET). Therefore

as

e-+O

(6.7)

::

-

a:

1

jJ!

(W~),n)a+1

(W~),m)b

(,Pdxdr

aRN

t

-

b!

1 J J (

w~),n)

a !

(wtk),m)

b+l

(?dxdr.

aRN

Since

n>m

+

1,

.

(

+

)a

{)

(+

)b+l

(

)a

{)

(

)b+l

w(k),n

Or

w(k),m

=

wtk),m

Or

wtk),m

-

w+

b+

1

{)

(

)a+b+l

- a + b + 1

Or

(k),m

'

a.e.ET.

We

obtain from (6.7)

(6.7')

c::

-

a:

1 J

(wtk),n)

a+l

(wtk),m)

b

(Pdx

RNX{t}

b

J(

)a+b+

1

-

(a

+

l)(a

+ b +

1)

w~),m

(Pdx

RNX{t}

.

+

a:

1 J

(wtk),n)

a+1

(w~),m)

b

(Pdx

RNx{a}

+

(a

+

1)(:

+ b +

1)

J

(wtk),mf+b+

1

(Pdx.

RNx{a}

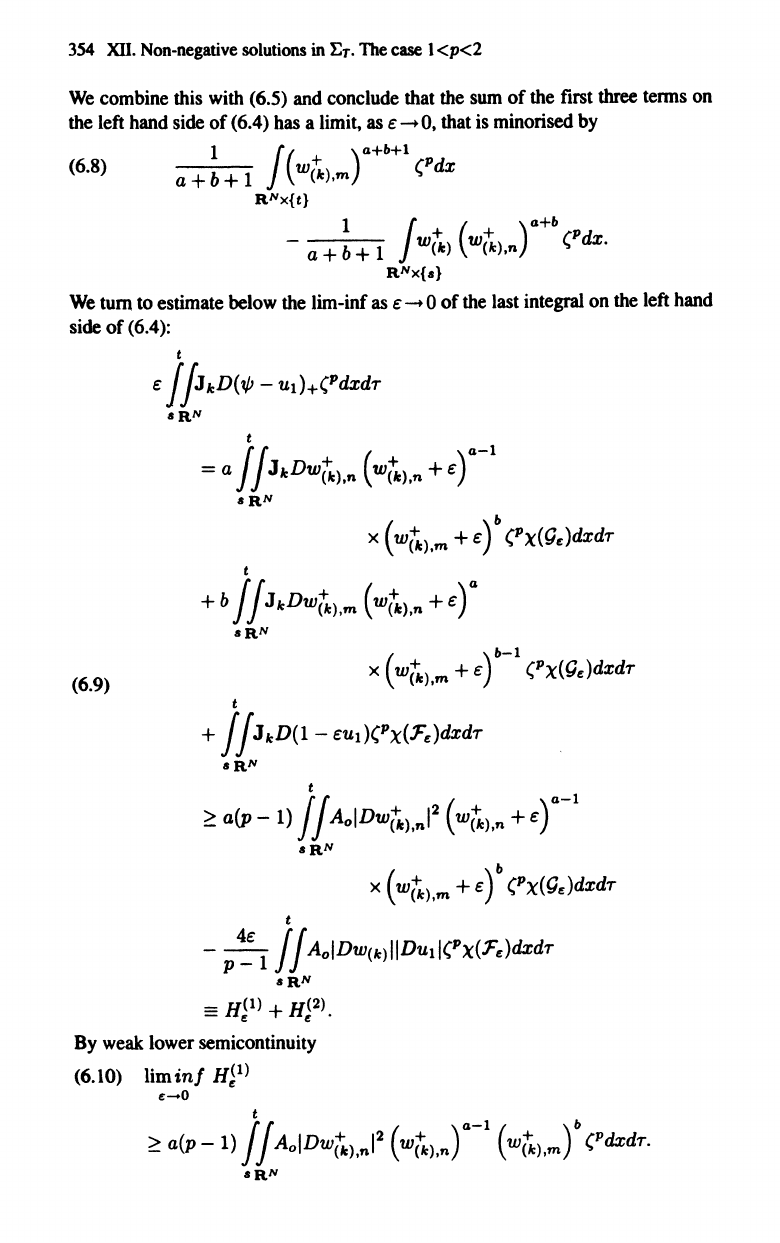
354

XII.

Non-negative

solutions

in

I:T.

The

case

I <p<2

We

combine this

with

(6.5) and conclude that the

sum

of

the first three tenns on

the left hand side of (6.4)

has

a limit,

as

€ _

0,

that

is

minorised

by

(6.8)

1

I(

)4+11+1

a + b + 1

w~),m

("dx

aNx{t}

1 f (

)4+11

- a + b + 1

w~)

w(k),n

("dx.

aNx{s}

We

tum to estimate below the lim-inf

as

€ - 0

of

the

last integral on the left hand

side

of

(6.4):

t

€

IIJIcD(1/J

-

ut}+("dxdT

saN

t

= a

II

JIcDw(k),n

(W~),n

+

€)

4-1

saN

t

+b

IIJIcDW~),m

(w~),n

+€)4

saN

(6.9)

t

+

IIJkD(I-€Ul)("x(.r~)dxdT

saN

t

~

a(p -

1)

II

AoIDw(k),nI2

(W(k),n

+

€)

4-1

saN

t

- p

~

1 I I

AoIDW(k)IIDull("x(.r~)dxdT

saN

==

H~I)

+

H~2)

.

By

weak

lower semicontinuity

(6.10) lim

in!

H~I)

~-o

t

~

a(p-l)

II

AoIDw(k),nI2

(W(k),nr-

1

(W(k),mt

("dxdT.

saN

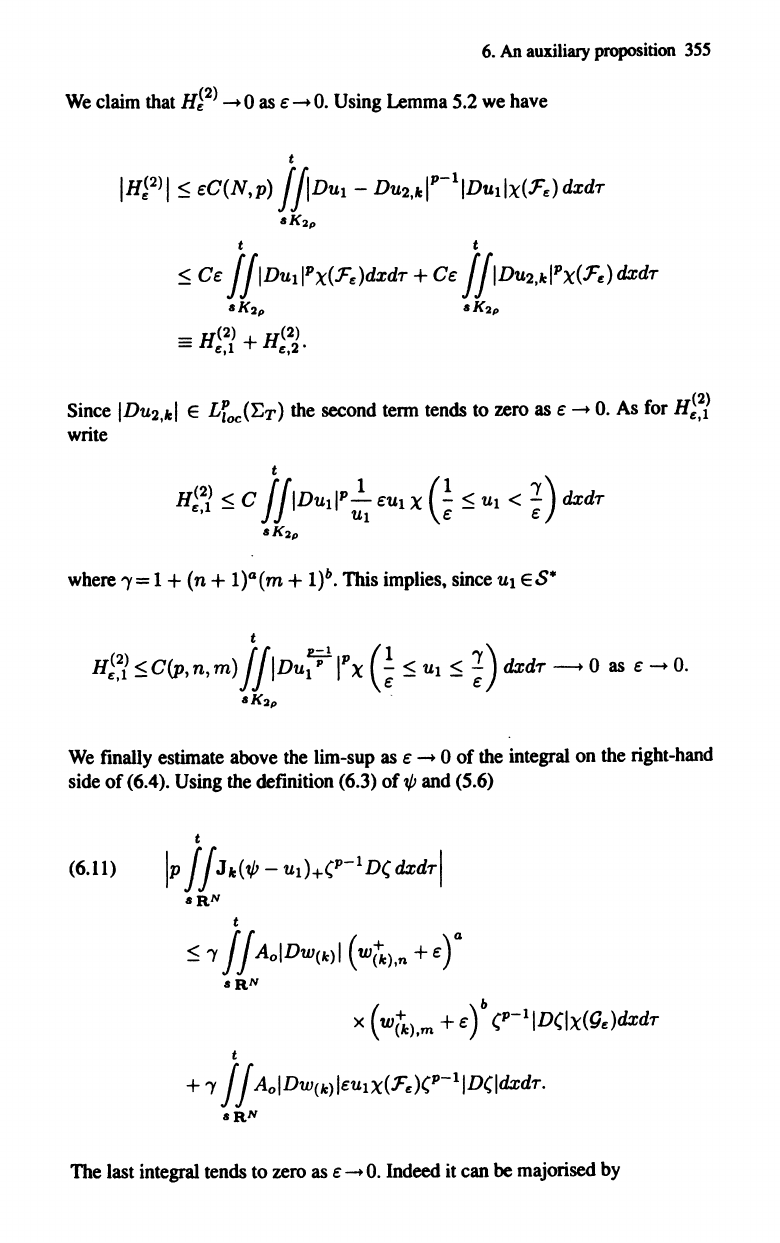
6. An auxiliary proposition 355

We claim that

H~2)

- 0 as € -

O.

Using Lemma

5.2

we have

t

IH~2)1

:5

€C(N,p)

jfiDUl

- DU2,IcIP-1IDullx(.rE)dxdr

aK

2p

t t

:5

C€ j jIDUIIPx(.rE)dXdr +

C€

j jIDu2,

Ic

I

P

x(.r

E) dxdr

SK2p SK2p

=

H(2)

+H(2)

-

E,l

E,2·

Since

IDu2,1c1

E LfoAET) the second tenD tends to zero as € -

o.

As for

H~~{

write

where

"1=

1 +

(n

+ l)G(m + l)b. This implies. since

Ul

ES·

t

H~~{

:5C(p,n,m)

jjlDu~IPx

(~

:5

Ul

:5

~)

dxdr

-+

0 as € -

o.

aK2p

.

We fmally estimate above the lim-sup as € - 0

of

the integral

on

the right-hand

side

of

(6.4). Using the definition (6.3)

of

t/J

and (5.6)

t

(6.11)

Ip

jjJIc(t/J-Ut}+(P-1D(dxdrl

saN

t

:5

"1

j j

AoIDw(lc)

I (

w~),n

+ € ) G

saN

t

+

"1

j j

AoIDw(lc)

IWIX(.rE)(P-l ID(ldxdr.

saN

The last integral tends

to

zero as € -

O.

Indeed it can

be

majorised by

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.