DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


356 XII. Non-negative solutions in
Er.
The case 1 <p<2
t
(6.12)
"(
!
jlDW(k)IP-1X(FE)
dxdr
BK~p
t
::;
"(
!!IDUlIP-1Xlul
~
~ldxdr
t
+"(
!!IDU2,kIP-1Xlul
~
~ldxdr,
BK~p
for a constant
"(
=
"((P,
n, m,
a,
b).
The second integral
on
the right hand side
of
(6.12) tends to zero as e
.....
O.
since
Ul
E Lloc(ET). As for the first integral,let
oE
(O,p
- 1) be so small that (0 +
l)(p
- 1) <
1.
Then
t
'Y
!!IDUt!P-1X[Ul
>
:ldxdr
BK~p
t
{f
-
(o+1)(p-l)
(o+l)(p-l)
=
'Y
11
IDullp-lul
p U
l
P
X[Ul
> : ldxdr
BK~p
t
-
{{
p-I-o
1
(o+l)(p-l)
=;:y
11
IDu
l
P I
P
- U
l
P
X[Ul
>
:ldxdr
BK~p
.1
<~IIDu
P-~-oIIP_l
(;
(u(a+l)(p-l)x[Ul >
lldxdr)P
- 1
P,KlpX(B,t)
11
1 •
BK~p
---+
0 as e
.....
o.
We
examine the lim-sup as e
.....
0
of
the first integral on the right-hand side
of
(6.11). The numbers k E R
+,
n E N being fixed,
if
e is small enough. we have the
inclusion
Moreover since
w~),n
E
Lfoc
(0,
T;
WI!;.;(R
N
))
We
write

(6.13)
6.
An
auxiliary
proposition
357
t
ffAoIDW(k)1
(w~),n
+ef
(w~),m
+e)b
(P-1ID(IX(Qe)dxdT
BRN
t
=
ffAoIDW~),nl
(w~),n
+ef
(w~),m
+e)b
(P-1ID(ldxdT
aRN
t
+ f f
AoIDw~)I(n
+ e)a(m +
e)b(P-IID(lx[w~)
> nlx(Qe)dxdT
BRN
t
+ f f
AOIDw~)lea+b(p-IID(IX(Qe)dxdT
=
K~l)
+
K~2)
+
K~3).
BRN
As
for
K~l)
the
integrand tends to
AoIDw~),nl(w~),n)a(
w~),m)b(P-IID(1
a.e.
K
2p
x (s, t),
in
a decreasing
way.
Therefore
t
K~l)
-+
f f
AoIDw~),nl(w~),nt(w~),m)b(P-lID(ldxdT.
BRN
The last integral tends
to
zero
as
e
-+
O.
Indeed
The operation
Dw~)
coincides with the
weak
derivative of
w~)
only
on
those
sets
Ai
where
w~)
is
bounded
by
a positive constant
i,
i.e.,
Dw~)x
(At)
==
Dw~),t.
Since
Dw~)
is
not well defined
a.e.
in
the
whole strip ET
we
estimate
K~2)
as
follows:
t
K~2)
-:;
'Y
(m
~
l)b
ffiDUl
-
DU2,kIP-lu~X[Ul
> n +
U2,k]X(Qe)
dxdT
aK2p
t
-:;
'Y
(m
~
l)b
ffIDUIIP-IU~X[Ul
>
n]x(Qe)
dxdT
aK2p
b t
(m+l)
ff
1 a
+
'Y
Up J J I
DU
2,kI
P
-
UIX[UI
> n +
U2,k]X(Qe)
dxdT.
aK2p
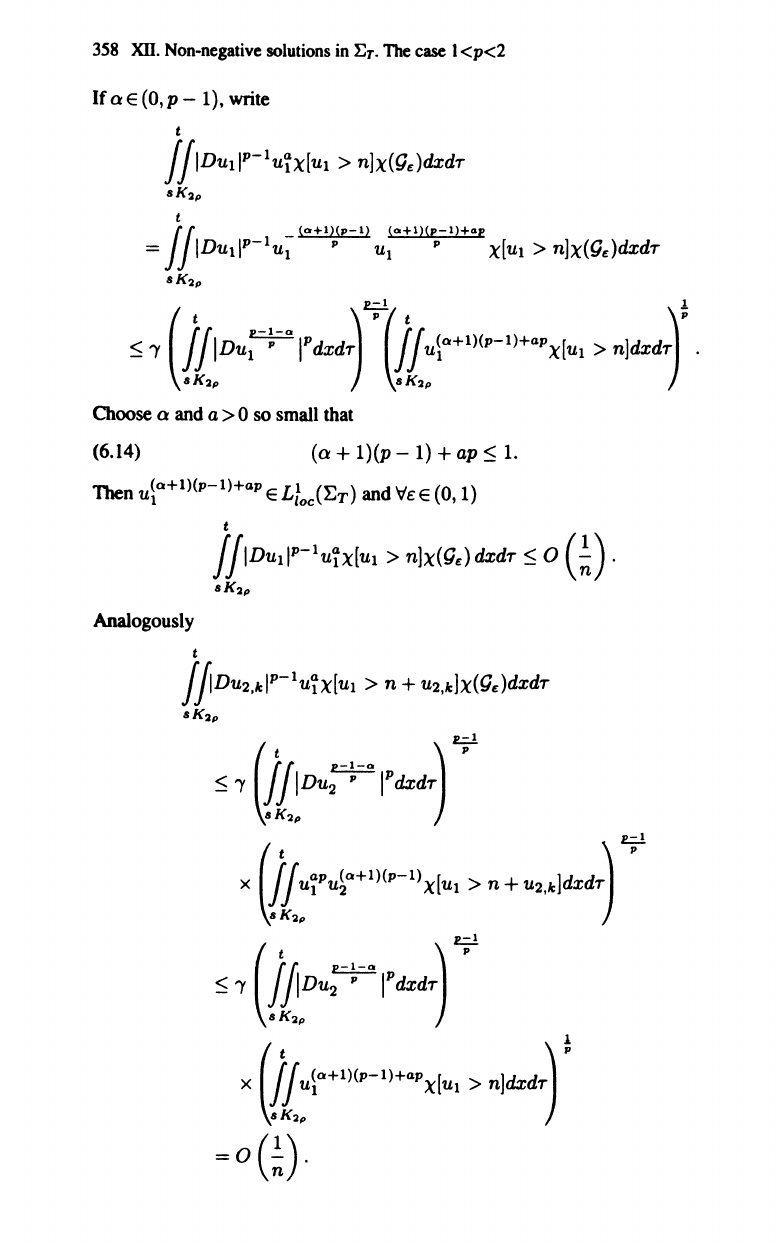
358
XII.
Non-negative
solutions
in
Er.
The
case
I
<p<2
If 0 E (O,p - 1).
write
t
JJIDUIIP-IU~X[UI
> n]x(ge)dxdr
aK2p
t
=
JJIDUIIP-IU~(O+l~P-l)
ut+1)(~-ll+GP
X[UI
>
n]x(ge)dxdr
aK2p
c.!
!
~
"(
(j
jIDu:-
:-°
1
,
/hd)
• r j j
.\0+1
)(,-1
)+«,
xl' 1 > n]dzdT Y
BK2p
')
~BK2P
')
Choose
0
and
a>
0
so
small
that
(6.14)
(0 +
1)(P
-
1)
+ ap
~
1.
Then
u~Q+l)(p-l)+ap
E
Ltoc(ET)
and
VEE
(0,1)
t
JJIDUIIP-IU~X[UI
> n]x(ge)dxdr
~
0
(;).
BK2p
Analogously
t
JfiDU2'kIP-IU~X[Ul
> n +
U2,k]X(ge)dxdr
aK2p
c.!
x
(jj
,:'u!,°+')('-')xl"
> n + ....
]dzdT
I ·
BK2p
)
~
"(
(jfiD'~
I'dzd)
....
BK
2p
)

6. An
auxiliary
proposition
359
We conclude that
provided
0:
and a> 0 are chosen
so
that (6.14) holds. Combining these estimates
and limiting processes as parts
of
(6.4) we obtain
1
J(
+ )a+b+l
a + b + 1
w(k),m
(P
dx
RNx{t}
t
+
a(p
-
1)
J J
AoIDw~),~J
(w~),n)
a-I
(w~),m)"
(Pdxdr
BRN
(6.16) $ a +
~
+ 1 J
wt
(w~),nr+"
(Pdx
RNx{a}
t
+
~JJAoIDW~),nl
(w~),nr
(w~),m)"
(P-1dxdr
BRN
+-y(m+ 1)"0
(~).
6-(iii).
The
limits
as
k--+oo and
8--+0
If
n E N and k > 0 are fixed, we let
iii{k),n
and
Dw~),n
be arbitrarily selected
but fixed representatives out
of
the equivalence classes
w~),n
and
Dw~),n
and
introduce the sets
where
C is the constant appearing in the last integral
on
the right hand side
of
(6.16). This integral is estimated as follows:

360
xn.
Non-negative
solutions in
~T.
The
case I <p<2
t
~
I I
AoIDw~),n
I (
w~),n
r (
w~),m)
b (P-
1
dxdT
BRN
t
$
~IIAoIDw~),nl
(w~),nr
(w~),m)b
(P-l
x
(tddxdT
BRN
t
+ (p
~~)qp
I
jlDw~),nIP-l
(w~),nr
(w~),m)
b
(p-1
X
(t
2
)dxdT
BRN
a(p-l)
jt!
2 (
)CI-l
(
)b
$ 2
AoIDw~),nl
w~),n
w~),m
(PdxdT
BRN
t
+
w+
w+
dxdT
4PCP
j!(
)P-l+CI
(
)b
aP-1(p _ l)p(qp)p
(k),n
(k),m
•
BRN
We carry this estimate in (6.16). move the integral involving
IDw~),nI2
on
the
left hand side and discard the resulting non-negative tenn to obtain
(6.17)
-y(P)
It
I(
)P-l+CI
(+
)b
+
(qp)P
w~),n
w(k),m
dxdT
B
K(1+")p
+
-y(m
+ l)bO
(~)
.
We let now k -
00
while B > 0, n,
mEN
remain fixed. Since
w~)
-
w+
in a
decreasing way we may pass
to
the limit under the integrals
in
(6.17) and obtain
the same integral inequality written for
w+.
In particular the first integral on the
right hand side takes the fonn
(6.18)
1 jw+(w+)CI+b(Pdx.
a+b+l
n
RNx{B}
Now letting s - 0. the integral in (6.18) tends
to
zero since it can be majorised
by
as
B -
O.

6.
An auxiliary proposition
361
These limiting processes yield
t
(6.19)
j(W:at+b+l
(Pdx
~
'Y(P)(~;)!
+
I)!
j(W:;y-1+
a
(W:a)b
dxdr
RNX{t}
OK(1+")p
+
'Y(a
+
b+
l)(m
+
l)bO(~).
6-(ivJ.
Proof
of
Proposition
6.1
We
let n
-+
00
in (6.19), while
mEN
remains fixed. The integrand in the
last integral tends to
(w+)p-1+a(w~)b
a.e. in
K(1+CT)p
x (0, t) in an increasing
fashion. Moreover
if
a is so small that
(6.20)
p - 1 + a E (0,1),
it is dominated, uniformly in n, by the function
The limit process gives
t
(6.21)
j(W~t+b+1
(Pdx
~
'Y(P)(~;)!
+
1)
j
J(w+)p-1+a(w~)bdXdT.
RNX{t}
OK(l+ ..
)p
This inequality holds true
"1m
E
N,
Vb
~
0,
"10-
E (0,1),
Vp
>
O.
The positive
number a is fixed, satisfying the restrictions
(6.14) and (6.20). The sequence
{w~}
increases to
w+
a.e. in E
T
.
Therefore as m
-+
00,
we may pass to the limit under
the integrals in
(6.21) for those b
~
0 for which
(w+)p-1+
a
+b
E Ltoc('ET).
If
b
i
~
0 is one such
b,
letting m
-+
00
we
find that
which implies that
(w+)p-1+a+bi+l
E Lloc(E
T
),
b
i
+l=b
i
+2-p>b
i
.
Let b
o
~
0 be defined by p - 1 + a + b
o
= 1. Then the previous remarks show that
(w+)p-1+
a
+b
o
+i(2-
p
)
==
(W+)1+i(2-
p
) E Ltoc(ET), i = 0,1,2,
....
Interchanging the role
of
UI
and U2 proves the Proposition.

362
XII.
Non-negative
solutions
in Er.
The
case I
<p<2
7. Proof
of
the uniqueness theorem
From
(6.1)
by
HOlder's
inequality, since
pE
(1,
2)
(7.1)
Let p > 0
be
fixed and for n = 1,2,
...
defme
Pn
= (t
2
-
i
)
p,
Kn = K
p
..
,
(1
-
2-(n+1)
n-
,
,=0
Rewrite (7.1) over Kn and
Kn+1
to
obtain
(7.2)
By
the interpolation
Lemma
4.3
of
Chap.
I
we
conclude that
for
every q E [1,00)
there
exists a constant -y=-y(N,p, q), independent of
p,
such that for all
tE
(0,
T)
(7.3)
To
prove
the
theorem
we
choose q so large that
N(p
- 2) +
pq
> 0
q
and
then,
such
a q being
fixed.
we
let
p-oo
in
(7.3).
8. Solving the Cauchy problem
We
will
establish
the
existence of a unique non-negative solution
to
the Cauchy
problem
(1.1)-(1.2) where
"0
is non-negative and merely in L}oc(RN). For n =
1,
2,
...
consider the sequence
of
approximating problems

9.
Compacbless
in
the
space
variables
363
(8.1)n
/:rUn
- div
IDu
n
l
p
-
2
DUn =
0,
in
ET
I
Un
E C (O,Tj L10c(RN»)nV
(0,
Tj
W,!;:(RN»)
( )
_ _
{min{uojn}
for
Ixl
< n
Un
x,O - U
on
= I I
'0
for
x
~n.
The
initial data are bounded
and
compactly supported
in
RN. Therefore
the
unique
solvability of (8.1)n can be established
as
indicated
in
§
12
of
Chap.
VI.
Since
the
initial data
{u
o
,n}f1S\l
form
an
increasing sequence of functions
in
Lloc<RN)
we
have
(8.2)
't/p>O.
The
solution of (1.1 )-(
1.2)
will
be constructed
as
the limit of
the
sequence
{u
n
}f1S\l
in a suitable
topology.
For this
we
establish
flJ'St
some
basic compactness of
{u
n
}f1S\l.
LEMMA
8.1.
There
exists a constant
"'(
=
"'(
N,
p)
independent
of
n
such
that
for
all
t,p>O
MoreoverforallaE(O,p-l),
PROOF:
The
Lloc-estimate follows from (4.1) with s = 0,
and
the
gradient
es-
timate (8.4)
is
a consequence of (4.2)
with
s =
O.
Finally (8.5)
is
the
content of
Lemma
3.2.
9. Compactness in the space variables
LEMMA
9.1. Let a E
(0,
p -
1)
be
so
small
that
(a
+
1)(P
-
1)
<
1.
There
exists
a constant ",(='Y(N,p,
a)
such
that
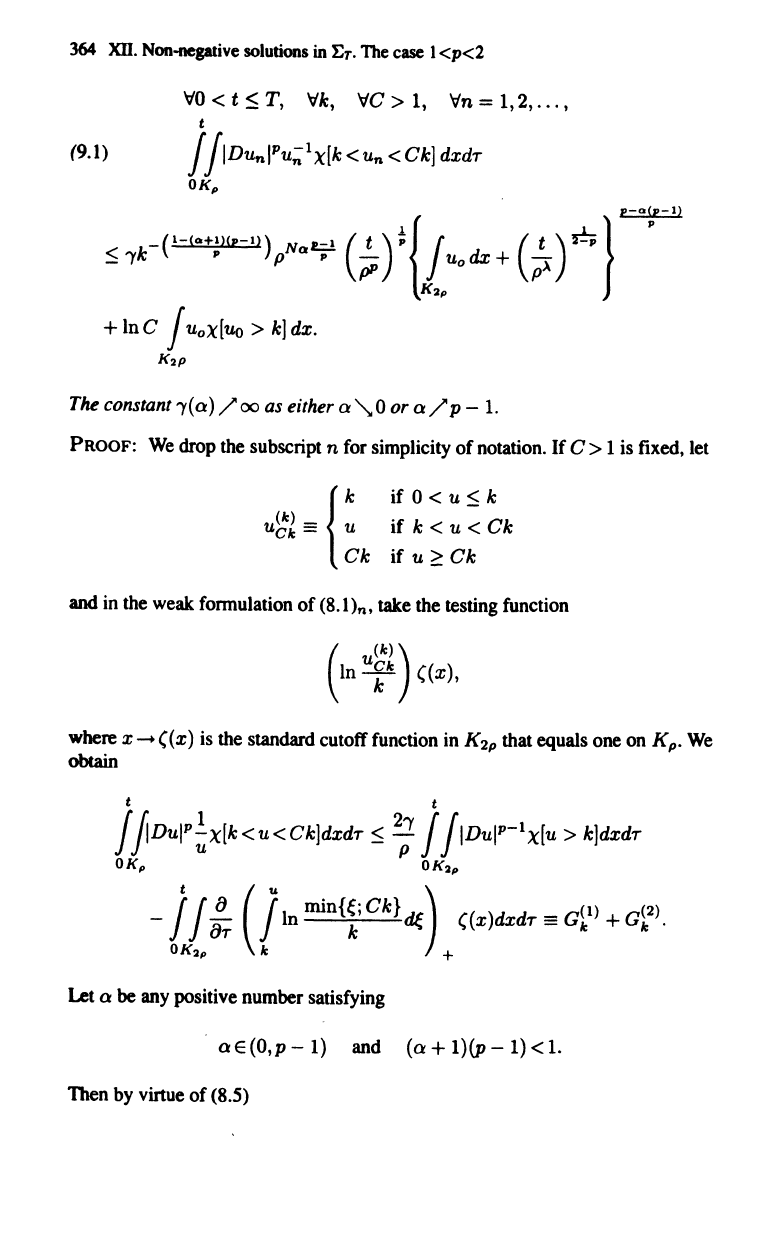
364 XII. Non-negative solutions in
I:T.
The case 1
<p<2
'VO
< t
~
T,
'Vk,
'VC
> 1,
'Vn
= 1,2,
...
,
t
(9.1) j jIDunIPu;;Ix[k<Un<Ck]dxdT
OKp
_(I-(QHHP-I»)
N
a
2=.l
(t
)~{j
( t
)~}P_Q~P_l)
<
'Vk
p P p - U dx + -
_ I
pP
0
p~
K3p
+
In
C j
uoX[Uo
>
k]
dx.
K3P
The constant
'Y(
0)
/00
as either
a'\.
0
or
0/
p -
1.
PROOF:
We
drop the subscript n for simplicity
of
notation.
If
C > 1 is fixed, let
U~~
==
{:
Ck
ifO<u~k
if
k < u <
Ck
if
u
2:
Ck
and in the weak formulation
of
(8.l)n,
take the testing function
(
(k))
In
U~k
((x),
where x
-+((x)
is the standard cutoff function in K
2p
that equals one on Kp.
We
obtain
t t
j
fiDUIP~X[k<U<Ck]dXdT:5
2;
j jIDuIP-1X[U > k]dxdT
OK
p
OK3p
-j j
:T
(i
In
min{~j
Ck}
de)
((x)dxdT
==
G~l)
+
G~2).
OK
b
k +
Let a be any positive number satisfying
.
OE(O,p-1)
and
(o+1)(p-1)<1.
Then by virtue
of
(8.5)
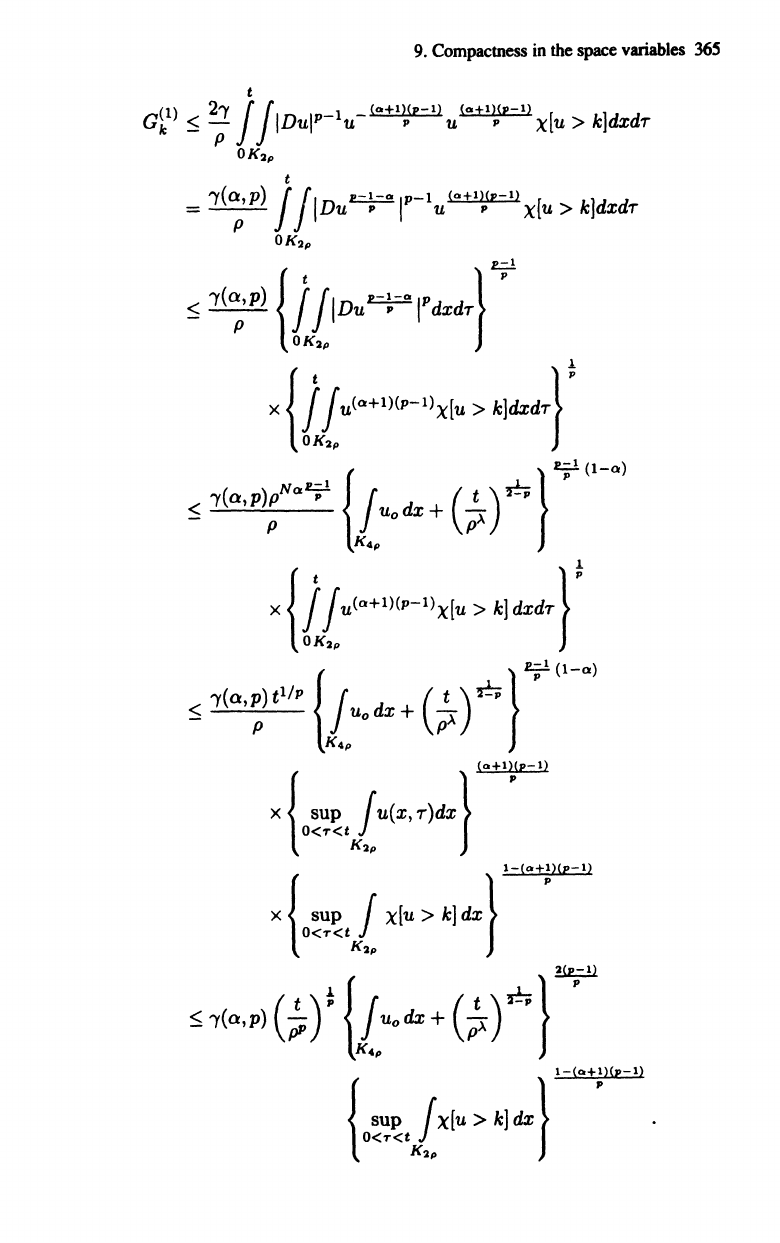
9.
Compactness
in
the
space
variables
36S
t
G
{l)
2')'
jjlD
IP-l -
(o+l)(p-l)
(o+l)(p-l)
[ j
k
~-
U U
pup
xu>kdxdT
p
OK2p
t
')'(a,p)
jilD
.-1-0
I
P
-
1
(0+1)(,-1)
[
kjdxd
=--
u
PUP
XU> T
p
OK2p
(0+1)(,-1)
X { sup
jU(X,
T)dx}
P
O<T'<t
K2p
1-(0+1)(,-1)
X { sup J
X[U
>
kj
dx}
P
O<T'<t
K2p
~
~')'(a,p)(~);{Juodx+(:~)~}
P
K4p
1-(o+l)(p-l)
{
SUP
jX[U>
kj
dx}
P
O<T'<t
K2p
