DiBenedetto E. Degenerate Parabolic Equations

XI

Non-negative solutions in

ET-

The case

p>2

1.

Introduction

Non-negative solutions of the heat equation

in

a strip ET

==

RN

X

(0,

T)

are

some-

what special

in

the sense that they grow

no

faster than

(1.1)

a < 1/4T,

as

Ixl-oo.

Let

I'

be

a

0'

- finite Borel measure in R N

with

no

sign restriction.

We

say

that

p.

bas the growth (1.1) if

(1.2)

/e-~ldlJl

<

00,

.

RN

where

IdILI

is the variation of 1'. Then

the

Cauchy problem

(1.3)

{

Ut

-

Llu

=

0,

in

E

T

,

u(·,O) = 1',

is

uniquely solvable within the class of functions satisfying (1.1).

The

• initial

mea-

slUe'

is

taken

in the

sense

(1.4)

/U(x,t)CPd/-L~

/cpd/-L,

as

t'\.O,

'v'cpEC~(RN).

RN RN

2.

Behaviour of

non-negative

solutions

as

lxi-

00

and

as

t

'\.

0

317

Conversely every non-negative solution

of

the heat equation

in

ET

verifies (1.4)

for some

u-fmite

non-negative Borel measure

Jl

satisfying the growth condition

(1.2). The measure

Jl

is unique and it

is

called the initial trace of u.

In

tum the

initial

trace

of

u determines u uniquely. These are the basic elements of a classical

theory developed by Tychonov

[98], Tacklind [94] and Widder [105]. A perhaps

rough summary of the theory

is

that the structure of

all

non-negative solutions of

the heat equation

is

determined

by

the heat kernel

1

_~

r(x,

t) =

(411't)N12

e

t,

t >

O.

Consider now non-negative local weak solutions

in

ET

of

{

u

E C

loc

(O,T;

L~oc(RN»)nLroc

(0,

T;

WI!;:(R

N

)) ,

p>2,

(1.5)

Ut

- div (lDulp-2 Du) = 0

in

ET.

The analog of

r(x,

t) for the degenerate p.d.e. (1.5)

is

the Barenblatt explicit so-

lution

~

(

)

_

-NI>.{

(IXI)P!Y}"-

B

x,

t = t 1 -

'Yp

til>'

+'

t >

0,

(1.6)

_....l...p-2

'Yp

==

A

,,-1

--,

A =

N(p

-

2)

+ p.

P

We

call this a 1undamental solution' only

in

the sense that

B(x,t)

--+

(411')

NI2

r(x,t)

pointwisein ET,

asp'\.2.

Solutions of (1.5) cannot

be

represented as convolutions of initial data

with

B( x, t).

Nevertheless the sup-estimates of Chap. V and the global Harnack estimates of

§7

of Chap.

VI

permit a precise characterisation

of

the

class of non-negative solutions

of

(1.5)

in

the whole E

T

•

with no reference to possible initial data. Such a charac-

terisation essentially says that all non-negative solutions of

(1.5) behave

as

t

'\.

0

like

the

'fundamental' solution B(x, t). and

as

lxi-

00

they grow

no

faster than

Ixl

p/

(p-2).

For these solutions

we

will establish the existence of initial traces and

prove their uniqueness

when

the

initial datum

is

taken

in

the sense of

Lloc<RN).

2.

Behaviour of non-negative solutions

as

Ixl-+

00

and

as

t'\.O

Let u

be

a non-negative local

weak

solution of (1.5)

in

E

T

•

For e E (0,

T)

and

r > 0

set

- J

u(x,r)

IIlulllr.T-~

= sup sup >'I(

-2)

dx,

O<T:$;T-e

p>r

P p

Kp

A=N(p

-

2)

+ p.

318

XI.

Non-negative

solutions

in

~T.

The

case

p>2

THEOREM

2.1.

There

exists a constant 'Y='Y(N,p)

such

that/or all

eE

(0, T),

{

;!,

}>./P

(2.1)

IIlullr,T-~

$ 'Ye-p!-, 1 +

(~)

p-

u(O,T-e)

Moreoverforall

tE

(0,

T-e),

and all

p~r,

(2.2)

pp/(p-2)

pI>'

lIu(·,

t)lIoo,Kp $

'Y

tNt>.

IIlullr,T-~'

t

(2.3)

j

jlDulP-IdxdT

$

'Y

tl/>'pl+~

Ilull!~~,

OKp

(2.4)

p2/(p-2)

2/

>.

IIDu(',

t)lIoo,K

p

~

'Y

t(N+l)/>'

Ilullr,T_~'

Moreover

(x, t)

-+

Du(x,

t)

is

Holder

continuous

in

Kp x

(e,

T

-e)

with

HOlder

constants and exponent

depending

only

upon

N, p,

'Y,

p, e and

IIlullr,~.

Remark

1.1. The functional dependence

of

these estimates is optimal as it can be

verified for the explicit solution 8(x, t).

Remark

1.1. The estimates (2.2)-(2.4) hold for solutions

of

variable sign. pro-

vided

we

assume (2.1).

PROOF

OF

THEOREM

1.1:

The estimate (2.1) is the content

of

Corollary 7.1 of

Chap. VI. whereas (2.2) follows from Theorem 4.5 of Chap.

V.

The

gradient bound

(2.3) is Lemma 9.1

of

Chap. V and

Remade

9.2. Inequalities (2.2)-(2.3) hold for a

time interval

(2.5)

for a constant

'Y.

='Y.(N,p). In view

of

(2.1) they

can

be considered valid for all

tE

(0,

T-e).

Indeed working within E

T

•

we

may state them for every substrip

RN x

[tl'

t2j,

O$t!

<t2

~T-e,

t2

-

tl

~

'Y

..

llullr,T-~'

In the proof

of

(2.4)

we

will work in the time interval (2.5).

We

begin with a

qual-

itative information.

LEMMA

2.1.

For

every

e E (0,

T)

and for

every

r > 0

the

quantities

IIDu(·, t)lIoo,K

p

sup

2/(

-2)

p>r

P P

arefinitefor all

0<

t~

T-e.

PROOF:

By the interpolation Theorem

5.1'

of

Chap. VIII with e=

1,

q =

1/2

and

9=!t

we deduce

3.

Proof of (2.4)

319

j

tj (

2)~

IIDu(·,r)lIoo,K

p

::;

'YP-(N+2) I

Du

l

P

-

1

dxdr +

~

,

OK

2p

for all r E

(it,

t). Estimating

the

right hand side

by

(2.3)

we

obtain

IIDu(·,r)lIoo,K

p

<

(ti

U

"l

p

-

2

)1/>'111

UI

+r~

p

2

/(p-2)

-

'Y

nUn

r,T-E

Un

r,T-1!

.

will

turn

such infonnation into

the

quantitative estimate (2.4).

3. Proof

of

(2.4)

Let

t>O

and

p>r

be

fixed and consider

the

box

Qo==K2pX

[it,

tleET.

Let

the

radii

{Pn}

and time levels {t

n

}

be

defined

by

n = 0,1,2,

...

and introduce the corresponding family of nested shrinking cylinders

Qn

==

K

pft

x{tn,t},

with vertex at

(0,

t).

We

will

estimate the quantity

IIDu(·,

t)lIoo,K

p

'

by

using

the

techniques developed

in

Chap.

VIII.

The starting point

is

the

the iterative inequality

(5.4)

in

that chapter, which

we

rewrite here

in the

context of the cubes

Qn

as

y.

<

bnk-~'LIy'l+~

n+1

_

'Y

+

"n

,

~2

==

N(p

-

2)

+

2p,

where

Y

n

==

j

jODu

l

-

kn)~

dxdr,

12ft

(3.1)

'It

==

{sg~

IDul

p

-

2

p-2

+

t-

1

},

and k is a positive number

to

be

chosen.

By

Lemma

4.1

of

Chap.

I,

the

sequence

{Y

n

}

tends

to

zero

as

n-+oo

if k is chosen

to

satisfy

We

conclude that there exists a constant

'Y

=

'Y(

N, p) such that

for

all

it::;

r::;

t,

(3.2) IIDu(., r)lIoo,K

p

::;

'Y'It~

(j

jlDulPdXdr)

2/>'2

t/2

K2p

320 XI. Non-negative solutions in E

T

•

The case

p>2

To

proceed

we

introduce the non-decreasing function of t

(3.3)

A>(

) _

¥-

IIDu(·,

T)lIoo,K

p

.....

t = sup T sup

2/(

-2)

,

O<r$!

p>r

p P

By

Lemma

2.1

and

(2.2) this quantity

is

well

dermed.

In

the estimates below

we

write

~

==

~(t)

if

the

dependence

upon

t

is

unambiguous.

We

estimate the quantity

1t introduced

in

(3.1)

by

and

deduce

from

(3.2) that

for

alllt

~

T

~

t

and

(3,4)

Estimating G1(t)

we

have

3.

Proof

of

(2.4)

321

t

G1(t)

~

'YiP

12 T

-:r

(N+2)(p-2)

{!

(N+l~P-2)

T1'[±l

P

t/2

(

IIDu(.,T)/lOO.Kp)P

d

}2/>'2

X

!~e

p2/(p-2)

T

To estimate G

2

(t) we refer back to the p.d.e. in (1.5). Let ( be a non-negative

piecewise smooth cutoff function in

K4pX{

it,

t} that equals one

on

K2pX{ !t,

t}

and such that

ID(I

~

2/

p and

(t

~

4/t. Taking u(P in the weak formulation

of

(1.5) we obtain

In

estimating G

2

(t) we use the estimation (2.2) and the range (2.5)

of

t.

Combining these estimates in (3.4) gives for all 0 < t

~

'Y.lllu~I;,7-E'

322 XI. Non-negative solutions in

Er.

The case

p>2

t

!

(N+1~(p-2)

1

2/>-

~(t)

~

l'

T

¥-

(T)dT+1'I~ullr,T_€'

o

for a constant 1'=1'(N,p). It follows that

~(.)

is majorised by the solution

of

{

V'(t)

~

l'

t-

(N+l¥P-2)

Vp-l(t),

V(O)

=

1'III1£II~:;_€,

0 < t

~

1'.m1£II~:;_€.

Solving this explicitly gives

1berefore choosing

t so small that

{

2/>-}-1/(P-2)

1 -

l'

(t

1~1£II~,T2_€)

~

2,

we will have

t¥

IID1£(·,

t)lioo,K

p

< 2

1111£11

2

/>-

p2/(p-2)

-

l'

r,T-€

for all such t and all

p>

r.

4. Initial traces

THEOREM

4.1.

Letubea

non-negative local weak solution 0/(1.5) in

:E

T

.

There

exists a unique Radon measure

p.

such that

(4.1)

lJ$

J

1£(x,

t)cpdx = J

cpdp.,

VcpEC~(RN).

RN

Moreover.

as

lxi-

00.

p.

'grows'

at

most

as

IxI

P

/(p-2).

Precisely.

(4.2)

f

dp.

sup

/(

-2)

<

00,

p>r

pP

P

Vr

>0.

Kp

PROOF:

The existence

of

a Radon measure

p.

satisfying (4.1 )-(4.2) follows from

the global Harnack estimates

of

§7

of

Chap. VI. Indeed by Corollary 7.1

of

that

Chapter, for every cube

[x

o

+ K

pj

C RN and all

cp

E Cr;'

(K

p),

1/

1£(X,t)cp(X)dXI

~

1'(N,p,p,T,u(x

o

,T-e))

Iicplioo,K

p

'

_ Kp

5.

Estimating

lDur-

1

in

Er

323

for

all

0 < t $

T-e

and

all e E

(0,

T). Therefore {u(·,

t)}O<t<T-€

is

a

net

of

equibounded linear operators

in

C~(RN),

and

for a subnet, indexed

with

t',

for

a

Radon

measure

IJ.

The

uniqueness of

such

a

measure

is

a consequence of

the

following:

LEMMA

4.1. Let u

be

a non-negative local

weak

solution

of

(1.5)

in

ET.

Then

Vp>O,

VUE(O,I),

VO<r<t

<T/2,

(4.3) f u(x, t)dx

~

f u(x,

r)dx-

;,(t -

r)l/'\p~

Ilull~;'~.

K(1+")p

Kp

PROOF:

Fix

0 < r < t

and

u E

(0,

1),

and

let

x _

'(x)

be anon-negative

piecewise

smooth cutoff

function

in

K(1+cr)p

that equals

one

on

Kp

and

such

that

ID'I

~

2p/u.

In

the

weak

formulation of (I.S)

take

,

as

a testing

function.

Integrating

over

(r,

t)

gives

t

f u(x, t) dx

~

f u(x,

r)

dx - u

2

p f

PDuI

P

-

1

dxds.

K(1+")p

Kp

T

K(1+")p

To

prove (4.3)

we

estimate the

right

hand

side

of this inequality

by

(2.3).

We

now

prove

the

uniqueness part of

Theorem

4.1.

Suppose

that

out

of

the

net

{u(x,

t)}O<t<T-€

we

may

select two subnets indexed

with

r'

and

t'

such

that

for

all

'P

E

C~(RN)

and

IJ

:/=

II.

Then

we

let r - 0

along

r'

in

(4.2)

and

then

let

t - 0 along t'.

This

gives

Interchanging

the

role

of

IJ

and

II

proves

the

Theorem

since

u E (0,1)

is

arbitrary.

5. Estimating

IDul

p

-

1

in

ET

Local integral estimates of I Dul

p

-

1

are

crucial

both

in

the global

Harnack

estimate

of

§7

Chap.

VI

and

in

the

theory of initial traces.

The

inequality (2.3) of

Theorem

324 XI. Non-negative solutions in

ET.

The case

p>2

2.1 is local but holds for all p >

r.

Therefore it implies some control

on

the be-

haviour

of

IDul as

lxi-

00.

This behaviour can be given

an

integral form,

by

means

of

the weights

(5.1)

where a is a positive number satisfying

.x

ap=

--2

+u,

p-

(5.2)

for some u >

O.

THEOREM

5.1.

Letu

bea

non-negative local weak solution of(1.5) in ET. Then

for

every u >

0,

there exists a constant

'Y

= 'Y(N,

p,

u) such that

for

all r > 0 and

all

EE

(O,

T),

(5.3)

sup

ju{x,

t)Aa(x)

dx

~

'Ylllullr,T-E'

O<t<T_

- aN

t

(5.4) j j1Du1P-1

Aa(x)

dxd-r

~

'Ytl/>'llull~;'~.

oa

N

Remark

5.1. The constant 'Y{N,p, u)

/00

as

u

'\,0.

PROOF

OF

(5.3):

Without loss

of

generality we may assume that r =

1.

Then

forallO<t~T-E,

ju(x,t)Aa(X)dx

~

j

u(x,t)Aa(x)dx+

f:

j

u(x,t)Aa(x)dx

aN {lzl<l}

n=O

{2n<lzl<2n+l}

00

~

mU~lr.T-E

+

2~

L

2-

an

mullr,T-E.

n=O

PROOF

OF

(5.4):

It will suffice to establish the estimate for t in the interval (2.5).

We will use this fact with

no

further mention. First we observe that the inequality

(5.5)

holds for all x E

RN

and all 0 < t

~

T-E.

This is obvious

if

Ixi

~

r with the

constant

'Y

depending also upon

r.

If

Ixi

>

r,

we apply (2.2) to the cube K

21zl.

Let

1/

E

(O,

T

~

) and in the weak formulation

of

(1.5), take the testing function

(t

)

l/p

i_a

(A

1

/P

r)P

-

11

+ U p

a+

1

'>

,

p

where x -

«x)

is the usual cutoff function in

Kp.

After a Steklov averaging

process and standard calculations,

we

obtain

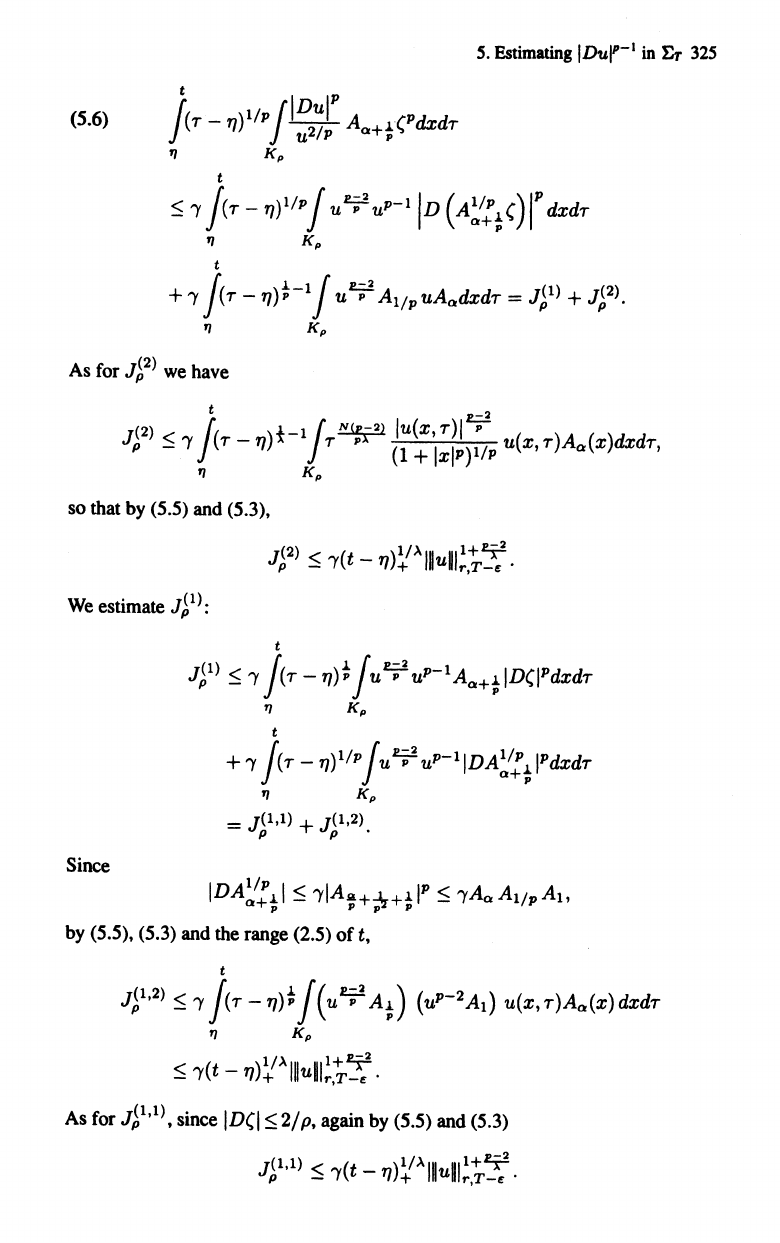
5.

Estimating

IDul

p

-

t

in

Er

325

(5.6)

t

}

(r

-

"l)I/p/IDU

IP

A 1.(Pdxdr

u

2

/

p

"'+,.

"

Kp

t

$

'Y

/(r

- "l)1/

P

/

u~up-1ID

(A~:i()IP

dxdr

"

Kp

t

+

'Y

pr

-

"l);-1/

u~

AI/puA",dxdr

=

J~1)

+

J~2).

"

Kp

As for

J~2)

we have

t

£=l

J(2)

<

"'}(r

_ .,,)t-

1

/

r

N(:X

2

)

lu(x,r)I"

u(x

r)A

(x)dxdr

p -

/./

(1

+ Ixl

p

)1/p

''''

,

"

Kp

so that by (5.5) and (5.3),

J~2)

$

'Y(t

-

"l)VAI~ull!;'~.

t

J~1)

$

'Y

/(

r -

"l);

/ u

~

u

p

-

l

A",+; ID(IPdxdr

"

Kp

t

+'Y

pr-"l)I/p/u~up-IIDA~:iIPdxdr

"

Kp

=

J~l,l)

+

J~I,2).

Since

IDA

1

/+

P

1.1

$

'YIA~+:\+1.IP

$

'YA",

A

1

/

p

At.

'"

,. ,.

,.

by (5.5), (5.3) and the range (2.5)

of

t,

t

J~I,2)

$

'Y

/(r

-

"l);

/

(u~

Ai)

(u

P

-

2

AI)

u(x, r)A", (x) dxdr

"

Kp

$

'Y(t

-

"l)VAlilull!;'~

.

As for

J~l,l)

, since ID(I $

2/

p,

again by (5.5) and (5.3)

J~l,l)

$

'Y(t

-

"l)VAlilull!;'~.

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.