DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


296
X.
Parabolic
,rsystems:
boundary
regularity
(2.11)
(2.12)
IBi
(x, t,
Dw)
I
:5
'Y
(1
+
IDwl,,-l)
,
Ihi (x, t, w,
Dw)
I
:5
'YIDul,,-2.
From
(2.1) and the definitions (2.3)-(2.4) and (2.6), it follows that
. I
1,,-2
N
(2.13)
Ai,l
(0,
O,~)
=
~
+ b
~i,1c
61c,i,
V
~
E R xm,
(2.14) b
==
(Di)
(0,0).
2 -(i).
Comparison
functions
Consider cylindrical domains of the type
where
'1
E (
-1,
1)
is
to
be
chosen,
Xo
E
K'R.
n { x N =
O}
and
the
faces
of the cubes
(xo
+
KR]
are
parallel
to
the coordinate'axes. These boxes
are
contained
in
Q'R.
if
(2.15)
which
from
now
on
we
assume. The proof of Theorem
1.1
is
based
on
comparing
w
in
a neighborhood of each point
(xo,
to)
E
Q'R./2
n { x N
~
O},
with
the solution
of
{
V
==
(Vl.V2,
...
,v
m
),
mEN,
(2.16)
vi,t-div
IDvl,,-2
DVi
=0,
in
[(x
o
,
to)
+ Q
(R2+'I,
R)]
nQ~,
Vi
=
Wi
on 8" [(x
o
,
to)
+ Q
(R2+'I,
R)]nQ~,
where 8"Q denotes the parabolic boundary of a cylindrical domain Q. The exis-
tence of a unique weak solution of
(2.16)
can
be
established
by
a Galerkin
proce-
dure.
(
1
)
Denote
by
(X,XN) , x
==
(Xl,X2,'.'
,XN-l),
the coordinates
in
K'R..
Then since w vanishes for x N = 0,
we
also have v(x, 0, t) =
O.
We
let v and W denote the odd extensions
of
v and w in the cylinder
[(x
o
,
to)+Q(R2+'I,R)ln{zN~o},
i.e.,
in
[(x
o
,
to)
+ Q
(R2+'I,
R)] n{XN
~
O}
in [(x
o
,
to)
+ Q (R
2
+'I, R)] n{XN
:5
a},
w
==
{ W(:,XN' t), in
[(xo,
to)
+ Q
(R2+'I,
R)] n{XN
~
O}
-W(X,-xN,t),
in
[(x
o
,t
o
)+Q(R2+'I,R)]n{xN
:50}.
Then,
by
the
reflexion principle v
is
the unique solution of
(1) See, for example, [73],

3. An iteration lemma 297
(2.17)
vi.t-div
IDvl
p
-
2
DVi
=0,
in [(x
o
,
to)
+ Q
(R2+'1,
R)]
,
{
V
==
(iit,V2,
...
, Vm),
mEN,
Vi
=
Wi
on 8
p
[(x
o
,
to)
+ Q
(R2+'1,
R)]
.
It follows from the interior estimates
of
Theorems 5.1 and 5.2'
of
Chap. VIII that
IDvl
is bounded in the interior
of
[(x
o
,
to)
+ Q
(R2+'1,
R)]
and it satisfies the
sup-bounds (5.1) and (5.3).
We
restate these bounds for the special geometry
of
[(x
o
,
to)
+ Q
(R2+'1,
R)].
THEOREM
2.1
(THE
DEGENERATE CASE
p>
2). Let v
be
the
weak
solution
of(2.17).
There
exists a constant 'Y='Y(N,p)
such
that for all
O<p'5.!R
(2.18) sup
IDvl
'5.
'Y
(R'1
ff
IDvIP
dxdr)
1/2
+
R-~.
[(zo.to)+Q(r+".p»)
)
[(zo.t
o
)+Q(R2+".R)
THEOREM
2.2
(THE
SINGULAR CASE max { Ii
A~2}
< p < 2). Let v
be
a weak solution of(2.17).
There
exists a constant'Y = 'Y(N,p)
such
that for all
O<p'5.!R
(2.19) sup
IDvl
'5.'Y
(R-
N
'1
ff
IDvl
P
dxdr)l/VP + Rr-.,
[(zo.t
o
)+Q(p2+".p»)
[(zo.to)+Q(W+"
.R)
where
IIp=N(P -
2)
+
2p.
Remark
2.1. Theorem 2.2 is a restatement
of
Theorem 5.2'
of
Chap. VIII with
q = p.
By
Remark 5.4
of
the
same Chapter, such a choice is admissible.
3.
An
iteration lemma
LEMMA 3.1. Let
8""!p(
8)
be
a non-negative non-decreasing function defined
in
[0,
I]
and satisfying
(3.1)
!P(p)'5.A(!JJ
!peR)
+
~A(R~-V"+"R-"),
VO<p
'5.
R'5.
1,
for
given
positive constants A,
{3,II,1\:
satisfying
in
addition
{3
> I\: and
II
E
(0,
1).
Then
for every
(3.2)
0'5. 6 < I\:
(1
~
~):):
{3)
,
there
exists a constant
'Y
depending
only
upon
A,
{3,11
and
6,
such
that

298
X.
Parabolic p-systems:
boundary
regularity
(3.3)
(
P )(j-tf,+6
cp(p)
~
'Y
R'
(cp(R)
+
1)
(1
-
v)1\:
VO<p~R~
1,
where
q = 1 +
f3
.
PROOF:
Choose
Ro
< 1 and define the sequence Rn+l =
~,
n =
0,
1,2,
....
Then
cp(Rn+1)
~
A~l-II)tf,cp(Rn)
+
~A
(
n!;'~"
+
~+~/,)
=
A~l-II)"cp(Rn)
+
A~+~/'.
Iteration of these inequalities gives
Now
and
Therefore if A
~
2
cp(Rn+1)
~
A
n
+1
(
~1
)
(j
cp(Ro)
+
2An+1l(+~/'.
Fix
6
in the
range (3.2) and set
E = I\:
(1
~
~):):
f3)
-
6;
f3
-
~
=
f3
- I\: + 6 + E.
Then
n+1
The first coefficient
in
(3.3)
is
independent of n if n
is
so
large that
AR~m
~
1.
Let
no
be
the smallest integer satisfying

4.
Comparing
w
and
v (the case p >
2)
299
qno+l
InA
-->--.
no
+ 1 -
I1nR~1
It follows from (3.3) that if n
~
no,
If
Ra
< 1 is fixed, for every p E (0,
Raj
there exist some n E N such that
Rf+l
~p~
Rtf.
Therefore the equation p =
R!,q"
has a root
(J
E
[I,
q]. Starting
the process with
Ra
replaced
by
R!,
gives
Remark
3.1.
The lemma continues to hold for 11=0. The constant
'Y
on the right
hand side
of
(3.3)
is
'stable'
as
11'\.0.
4.
Comparing w
and
v
(the
case
p>
2)
We
start
by
comparing w solution
of
(2.S) with the solution v
of
(2.16). Having
fixed
(xo,
to)
E Ql'R n {XN =
O},
we
may
assume, after a translation, that
it
coincides with the origin. Setting
the vectors
w and v satisfy
(4.1)
!
(Vi
-
Wi)
- div (IDvIP-2Dvi
-IDwIP-2Dwi)
= -
div(Ai(x,t,Dw)
- Ai(O,O,Dw»
- div (Ai(O,O,Dw)
-IDwIP-2Dwi)
- Bi(x, t,
Dw)
-
1:>8
Ii
leX,
t, w,
Dw),
in
+Q1t,
uXl
'
(4.2) Vi -
Wi
= 0
on
the parabolic boundary
of
+Q1t.
From (2.10) it follows that
IAi,l(X, t,
Dw)
-
Ai,t(O,
0,
Dw)1
~
'Y
R)..
(1
+ IDwIP-l),
for
i=I,2,
...
, m and 1.=1,2,
...
,
N.
Moreover from (2.13)
and
(2.14)
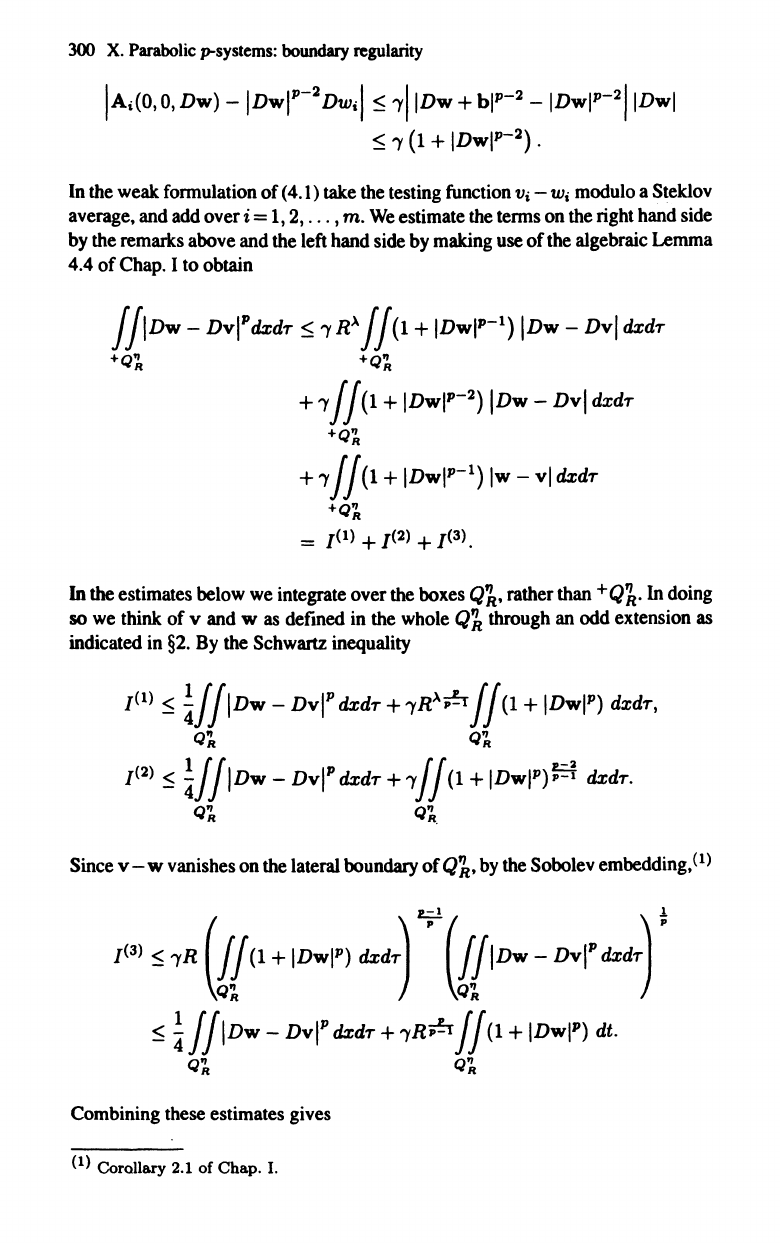
300
X.
Parabolic
p-systems:
boundary
regularity
IAi(O,
0,
Dw)
-IDwIP-2
DWil
~
'YIIDw
+
bl
p
-
2
-IDwIP-21IDwl
~
l'
(1
+ I
Dw
I
P
-
2
) .
In the weak fonnulation of (4.1) take the testing function
Vi
-
Wi
modulo a Steklov
average, and add over
i =
I,
2,
...
, m.
We
estimate the tenns on the right hand side
by
the remarks above and the left hand side by making use
of
the algebraic Lemma
4.4
of
Chap. I to obtain
//IDW
- DvlPdxdr
~
'YR).
//(1
+
IDwIP-1)
IDw
-
Dvl
dxdr
+Qlc +Qlc
+1'//(1
+
IDwIP-2)
IDw
-
Dvl
dxdr
+Qlc
+1'//(1
+
IDwIP-1)
Iw
- vldxdr
+Qlc
=
[(I)
+
[(2)
+
[(3)
.
In the estimates below
we
integrate over the boxes
Q'k,
rather
than
+Q'k.
In doing
50
we
think
of
v and w
as
defined in the whole
Q'k
through an odd extension
as
indicated in
§2.
By
the Schwartz inequality
[(I)
~
~//IDW
-
Dvl
P
dxdr+'YR).P!Y
//(1
+
IDwI
P
)
dxdr,
Q~
Qlc
[(2)
~
~//IDW-DvIPdxdr+'Y//(I+IDwIP)~
dxdr.
Q~
Q~.
Since v - w vanishes on the lateral boundary
of
Q'k,
by
the Sobolev embedding, (1)
z.::.!
.1
1(') S
~R
(If
(1+
JDwJP)
kdT)
,
(I/,Dw
-
DvI
P
dzdT
r
~
~//IDW-DvIPdxdr+'YRP!Y
//(1
+
IDwI
P
)
dt.
Qlc
Q~
Combining these estimates gives
(1) Corollary 2.1
of
Chap.
I.
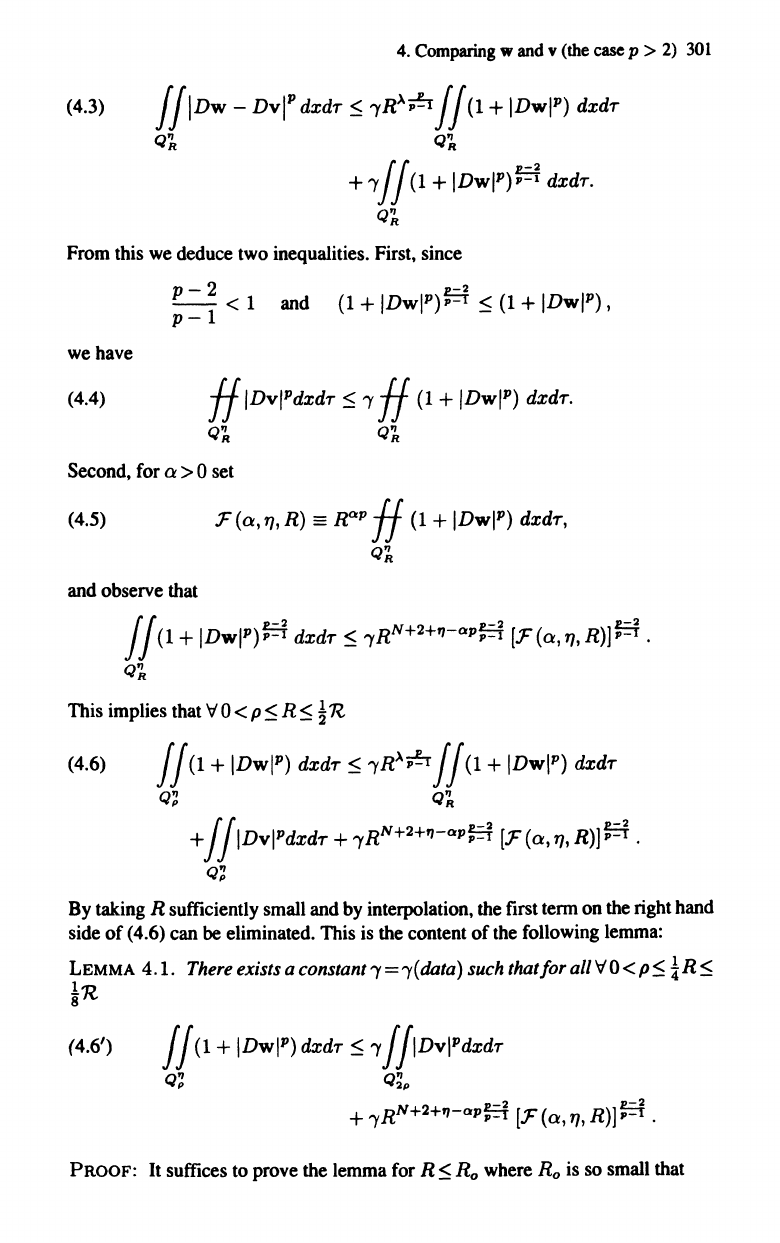
4.
Comparing
w
and
v (the case p >
2)
301
(4.3) //IDW -
DvlP
dxdr
~
"YR~t=r.
//(1
+
IDwI
P
)
dxdr
Q~ Q~
+
"Y//(1
+
IDwIP)~
dxdr.
Q~
From this
we
deduce two inequalities. First, since
p - 2 < 1 and
(1
+
IDwIP)~
~
(1
+
IDwIP),
p-l
we
have
(4.4)
If IDvlPdxdr
:5
"Y
If
(1
+
IDwI
P
)
dxdr.
Q~ Q~
Second, for
0:
> 0 set
(4.5)
:F
(0:,
"I,
R)
==
Rap
If
(1
+
IDwI
P
)
dxdr,
Q~
and observe that
//(1
+
IDwIP)~
dxdr
~
"YRN+2+,,-ap~
[:F(O:'''I,R)l~.
Q~
This implies that
VO<p~R~!n
(4.6)
//(1
+
IDwI
P
)
dxdr
~
"YR~t=r.
//(1
+
IDwI
P
)
dxdr
Q:
Q~
+ /
/IDvlPdxdr
+
"YRN+2+,,-ap~
[:F(o:,
"I,
R)l~
.
Q:
By
taking R sufficiently small and
by
interpolation, the first term on the right hand
side
of
(4.6) can
be
eliminated. This
is
the content
of
the following lemma:
LEMMA
4.1.
There
exists a constant
"Y
=
"Y(
data)
such
that
for all V 0 < p
~
1 R
~
In
(4.6')
//(1
+
IDwlP)dxdr
~
"Y!!IDvIPdxdr
Q:
Q;p
+"YRN+2+,,-ap~
[:F(O:'''I,R)l~.
PROOF:
It
suffices to prove the lemma for R
~
R"
where
Ro
is
so small that
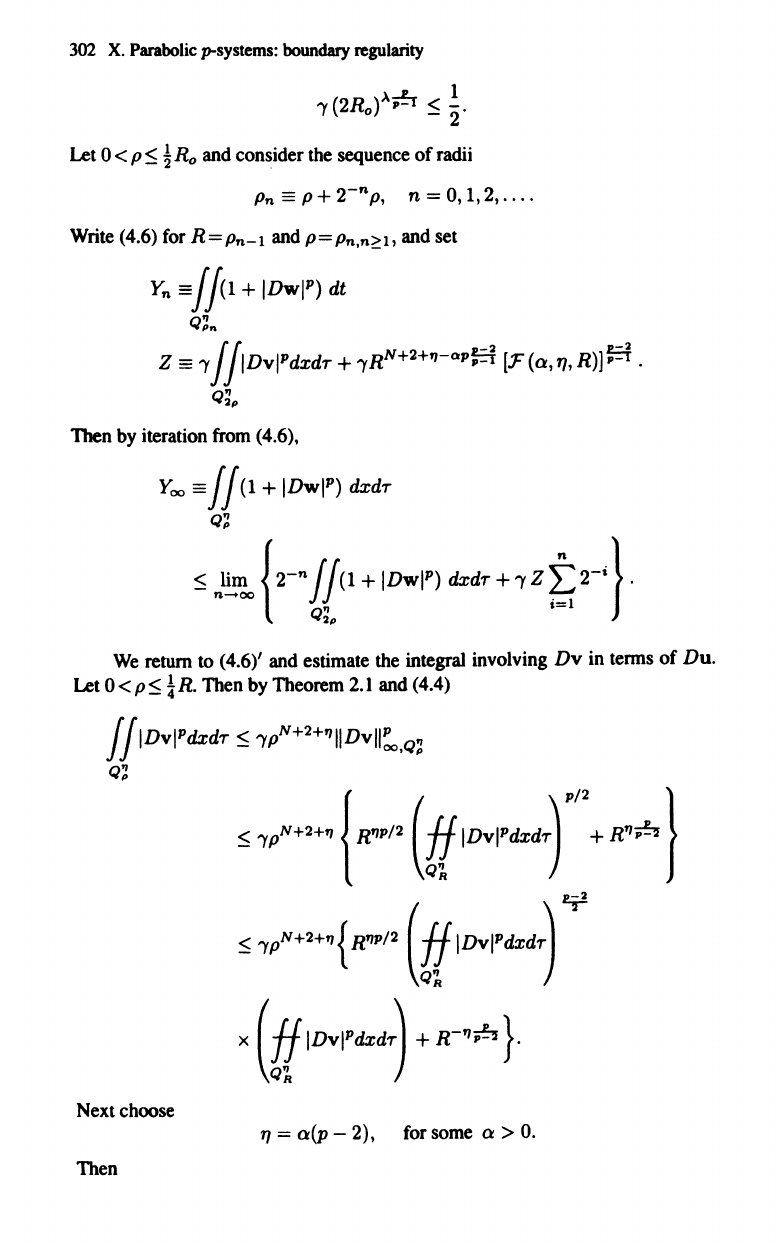
302
X.
Parabolic
p-systems:
boundary
regularity
'Y
(2Ro).\p!-r
~
~.
Let 0 < p
~
~
Ro
and consider the sequence
of
radii
Pn
==p+2-"p,
n=O,I,2,
....
Write (4.6) for
R=P,,-l
and
P=P",n~h
and set
Y"
==!
PI
+
IDwIP)
dt
Q:n
Z
==
'Y!!IDvIPdxdT
+
'YRN+2+71-ap~
[.r(a''1,R)l~
.
Q~"
Then by iteration from (4.6),
Y
oo
==//(1
+
IDwIP)
dxdT
Q:
We
return
to
(4.6)' and estimate the integral involving
Dv
in terms
of
Du.
Let 0 < P
~
!
R.
Then by Theorem 2.1 and (4.4)
/
/IDVIPdxdT
~
'YpN+2+71I1Dvll:a,Q:
Q:
Next choose
Then
,;
~pN+2+'
{
Jl!lPI'
(U
IDvIPdzdT)
pl'
+ R"-,!. }
~
,;
~pN+""'{
Jl!lPI'
(U
IDvIPdzdT)
x
(UIDvIPdzdT)
+
R-'-,!.}'
'1
= a(p - 2), for
some
a>
O.

4. Comparing w and v (the case p > 2) 303
~
Ir',/2
(u
IDvl'
do:dr
) "
~
[.1"
(Q,
.,
RlI'"
,
and
by
suitably modifying
the
constant
'Y
we
deduce
from
(4.6)' that
for
all
0 <
p~R~!,R.,
(4.7)
//(1
+
IDwI
P
)
dxdr
Q:
~
(p)N+2+'I
f f
~
'Y
[.1'
(a,
71,
R)l R
)}
(1
+
IDwlP)dxdr
Q1r
+'Y[F(a'71,R)l~
RN+2+'I-a~
+'YpN+2+'I R-ap,
for
a constant
'Y
=
'Y
(data). Set
(4.8)
F(a)
==
sup
{pap
H
(1
+
IDwI
P
)
dt}
(:Co,t
o
)EQR/2
O<pSRSR/2
[(zo,t
o
)+Q:l
and
(4.9)
We
summarise:
PROPOSITION
4.1. Let a > 0 and
71
=
a(p
- 2). There exists a constant'Y =
'Y
(data), independent 0/
a,
71,
p,
R,
such that
/orall
(xo,to)EQ:k/2
and/orall
O<p~R~'R./2,
(4.10)
//(1
+ IDwlP)dxdr
[(zo ,to)+Q;J
~
'Yg(a)(~)N+2+'I
/f
(1
+ IDwlP)dxdr
[(
Zo
,to
)+Q7tJ
+
'Yg(a)RN+2+'I-ap~
+
'YpN+2+'I
R-aP.
PROOF:
The previous arguments prove
the
proposition
for
those
points
(x
o
,
to)
EQ!Rn{XN
=O}.
The
estimate
is
obvious
for
boxes
[(x
o
,
to)
+
Q7tl
c
Q~,
by
interior estimates.
If
[(
x
o
,
to)
+ Qkl intersects
{x
N =
O},
then
either
(4.11) [(Xo,to)+Q1R]CQR or [(Xo,t
o
) +
Q1R]n{x
N
=O}#0.

304
X.
Parabolic p-systems: boundary
regularity
In
the first case
we
may establish (4.10) with R replaced by
~
R. The general case
follows
by
suitably modifying the constant "f.
If
the second
of
(4.11) holds,
we
let
(4.12)
X.
==
(Xo,l' X
o
,2,
.
..
,Xo,(N-l),
0)
and observe that
[(x.,
to)
+
Q1R]
C
[(xo,
to)
+
Qkl·
We
carry
on
the process leading to (4.10) for such a
new
box, for all
2X
o
,N
:5
p <
!
R.
This implies that (4.10) holds for all
Xo,N
<
p:5
!
R.
If
p:5
Xo,N,
we
consider
the cylinder
[(X
O
,
to)
+
Qt.N]'
which satisfies the inclusion
[(X
o,
to)
+
Ql
z
o,N]
c
Q:k.
Then
by
interior estimates, (4.10) holds with R replaced
by
Xo,N.
Combining the
two cases and suitably modifying the constant
"f
we
conclude that (4.10) holds for
-+
1
all (xo,to)e
QI'R.
and all O<p:5R:5
2'R.
5. Estimating the local average
of
IDwl
(the case
p>
2)
LEMMA
5.1.
For every 0: e (0,1) there exists a constant "f = "f
(0:,
data), such
thot
jorall
(Xo,
to)
e
Q:k/2
and/orall
0<p:5R:5'R/2,
(5.1)
H (I, +
IDwI
P
)
dxdr:5
"f(o:,data)
p-
QP
,
'1
=
o:(p-
2).
[(zo,to)+Q:l
PROOF:
Define the sequences 0:
0
=
(N
+ 2)/2 and for
n=
1,
2,
...
,
We
will prove inductively that
(5.2)
Since
IDwleLP(nT),
H
(1
+
IDwI
P
)
dxdr
:5
"fP-¥
P
(1
+
IIDwll:,nT)
.
[(zo,to)+Q:ol
Therefore

6.
Estimating
the
local
averages
of w
(the
case p >
2)
305
Suppose the lemma holds for Q
n
and let us show that it continues to hold for Q
n
+ 1.
If
F(Qn):'5
1'(Qn),
the quantity
Q(Q
n
)
introduced in (4.9) is bounded and we may
use
(4.10) with Q = Q
n
and
TI
=
TIn.
We
apply the iterative Lemma
3.1
to the
function
tp(p)
= J J
(1
+
IDwI
P
)
dxdr,
[(zo,to)+Q~l
with the choice
of
parameters
(5.3)
p-2
-
v =
--,
6 = 6
n
Q
np.
p-l
We
obtain
If
(1
+
IDwI
P
)
dxdr
:'5
1'(Qn+d
p-On+lP
(tp(R) + 1).
[(zo,to)+Q~n
1
Let 0 <
P:'5
'R/2 be fixed and consider the point
(xo,
to)
==
(0, 0). Without loss
of
generality assume that
p'r/n+l / p'r/
n
is an integer,
and partition the cylinder
[(x
o
,
to)
+
Q~n+l]
into s = p'r/n+l-'r/n adjacent boxes
with
'vertices', say (0, td, (0,
t2),
...
, (0, t
s
).
Then
If
(1
+
IDwI
P
)
dxdr:'5 p'r/
n
~
If
(1
+
IDwI
P
)
dxdr
p'r/n+l
~
Q:n+l
3=1
[(o,tj)+Q~nl
:'5
1'(Qn+l)
p-On+lP.
We
may treat analogously the other points
of
Q'R./2
and the inductive inequality
(5.2) follows. To prove the lemma it suffices to prove that
{Q
n
}
-.
0
as
n
-.
00.
The sequence
{Q
n
}
is deacreasing.
We
claim that { Qn}
-.
O.
Indeed
if
not,
lim Q
n
= Q
o
> 0,
n--+oo
and the definitions
of
{Q
n
}
and {6
n
}
would imply
Therefore
Qn+l
:'5
Qn(I-6
o
).
This in tum implies
{Q
n
}
-.0.
Remark
5.1. The constant
l'
on the right hand side
of
(5.1) is 'stable'
as
p
~
2.
This follows from the choice (5.3)
of
the parameter v and Remark 3.1.
6. Estimating the local averages
of
w (the case p > 2)
We
return to cylinders bearing the natural parabolic geometry, i.e., Q p
==
Q
(p2,
p)
and will work within the boxes
