DiBenedetto E. Degenerate Parabolic Equations

266

IX.

Parabolic

p-systems:

H61der

continuity

of Du

LEMMA

6.2.

There

exists

a constant'Y='Y(N,p)

such

thatforall

O<p~R

(6.8)

PROOF:

It

suffices to prove the lemma for 0 < p

~

R/2

N

+2.

Let

{

be

the standard

cutoff function

in

Q

R/2N

+ 1 that equals one on Q

R/2N

+2

and such that

ID{,

~

2N+2/R and 0 < (e

~

(2N+2/R)2.

IfO<p<R/2

N

+2,

we

have

(6.9)

!!lv

I2

dxdT

~

'YpN+2"v"~,Qp

~

'YpN+2"v{"~,QIl/2N+1.

Qp

On

the

other hand for all (x,

t)

eQR/2N+1,

t

Iv{l(x, t) = I !

De

(v()

(x,

T)dTI

~

'Y

!ID:

Dt(v{)1 dxdT

_R2/2

N

+1

Q

Il

/

2

N+1

Combining this

with

Lemma

6.1

we

obtain

the

estimate

"V{"~,QIl/2N+1

~

'YR-CN+2>!!lvI2dxdT.

QIl

This

in

(6.9) proves the

lemma.

PROOF

OF

THEOREM

6.1: Since the vectors vz",z. solve (6.3) for

h,s

=

1,2,

...

,

N,

we

have

from

Lemma 6.2

(6.10)

!!ID

2

v

I2

dxdT

~

'Y

(~)N+2!!ID2vldxdT'

Qp

QIl/2

for a constant 'Y='Y(N,p) and

for

all

0<p~R/2.

To

estimate the right hand side

of (6.10) observe that

the

vectors v z. solve the system

(6.11)

Let

W be

any

constant vector

in

R

Nxm

and

multiply

(6.11)

by

the

testing function

(Wi,z. - Wi,.)

(2.

where

( is

the

standard cutoff function

i.O

Q R that equals one

in

QR/2. This gives

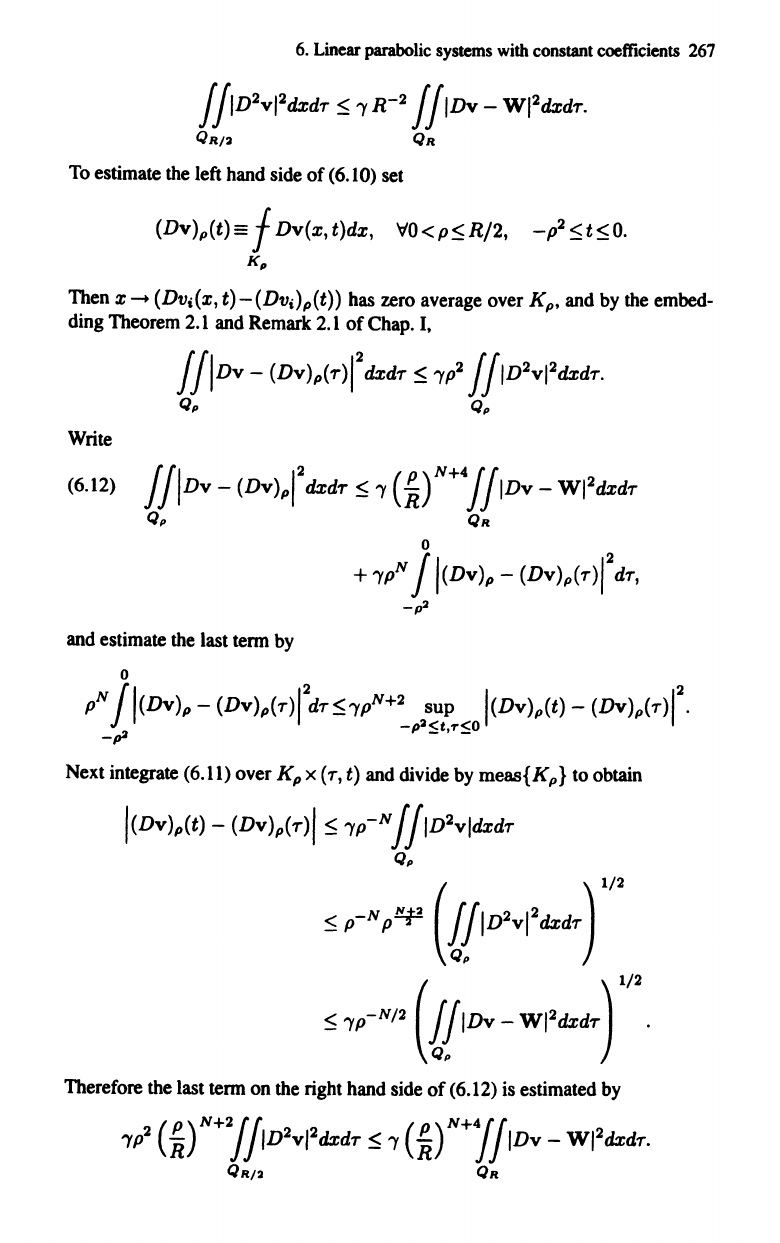
6.

Linear parabolic

systems

with

constant coefficients

267

/

/ID

2

v

I2

d3:dT

::s;

'Y

R-

2

//IDv

-

WI

2

d3:dT.

QIl/2

QIl

To estimate the left hand side

of

(6.10) set

(Dv)p(t)= f Dv(x,t)dx,

\:IO<p::S;R/2,

_p2::s;t::s;O.

K,.

Then

x-

(Dvi(x, t)-(DVi)P(t» has

zero

average over Kp. and by the embed-

ding Theorem 2.1 and Remark 2.1

of

Chap.

I.

/

/IDV

-

(DV)p(T)1

2

d3:dT

::s;

'Yp2//ID

2

v

I2

d3:dT.

Qp Qp

Write

(6.12)

//IDV

-

(DV)pI2

d3:dT

::s;

'Y

(~)N+4/fIDV

-

WI

2

d3:dT

Qp

QIl

and estimate the last

tenn

by

o

+

'YpN

/ I (Dv)p -

(DV)p(T)1

2

dT,

-p2

pN/I(Dv)p

-

(DV)p(T)1

2

dT::S;'YpN+2

sup I(Dv)p(t) - (Dv)p(T)r·

__

2<t,.,.<O

-p2

~-

-

Next integrate (6.11) over K p x (

T,

t)

and divide by meas{ K

p}

to obtain

I(Dv)p(t) - (Dv)p(T)/

::s;

'YP-N

/

/ID

2

vld3:dT

Qp

yN/'"

(£!ID'VI'dzdT)

1/'

$

~p-N/'

(£!IDv

_

WI'dzdT)

1/'

Therefore the last

tenn

on

the right hand side

of

(6.12) is estimated by

'Yp2

(~)N+2//ID2vI2d3:dT::S;

'Y

(~)N+'l/IDV

-

WI

2

d3:dT.

QIl/2

QIl

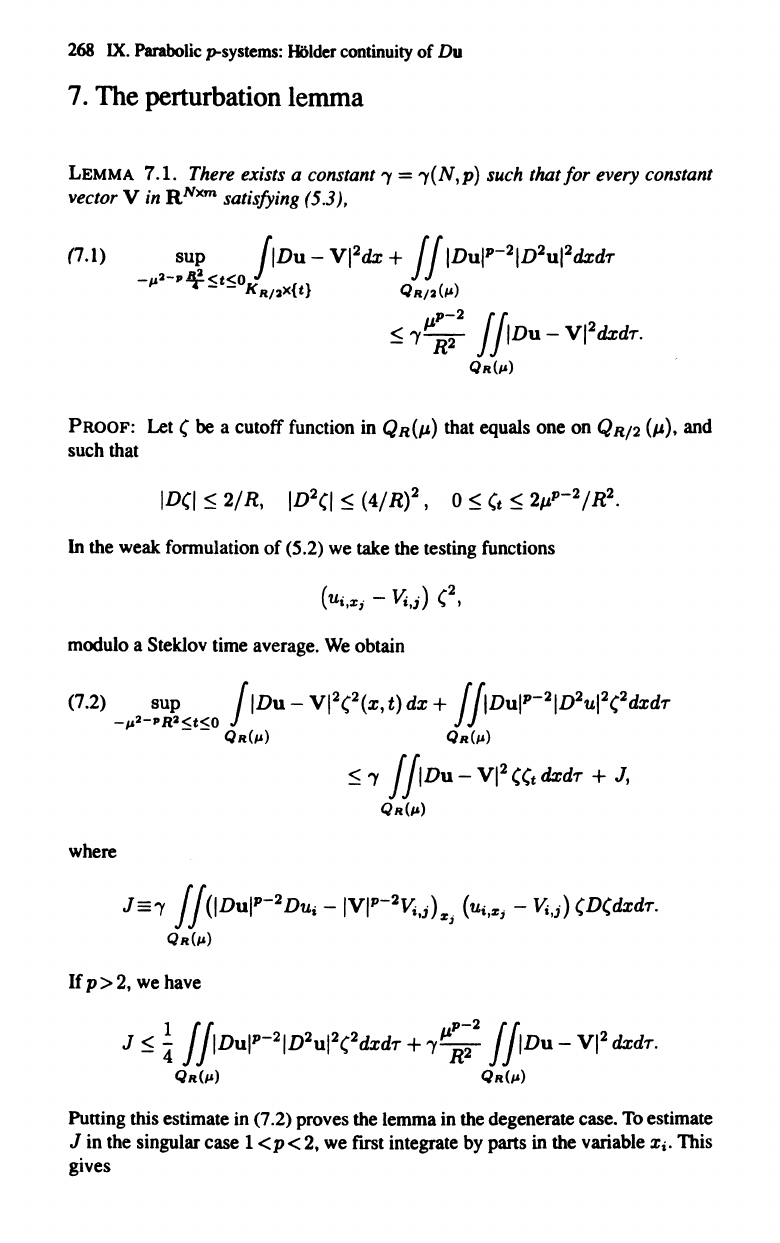
268

IX.

Parabolic:

p-systems:

mlder continuity of Du

7.

The perturbation lemma

LEMMA 7.1. There exists a constant

'Y

= 'Y(N,p) such

that/or

every constant

vector

V in RNxm satisfying (5.3),

PROOF: Let ( be a cutoff function in

QR(P.)

that equals

one

on

QR/2

(p.).

and

such that

In

the weak formulation

of

(5.2) we take the testing functions

modulo a Steldov time average. We obtain

(7.2)

sup

flDU

- VI2(2(X, t)

dx

+ f

fIDul,,-2ID2uI2(2dxdT

-,.2-PR2<t<O

J J I

where

- -

QR(,.)

QR(")

$;'Y ffIDU-VI

2

((t

dxdT

+

J,

QR("')

J='Y

f

fODUI,,-2DUi

-IVI,,-2Vi,;)z;

(Ui,z;

-

Vi,;)

(D(dxdT.

QR("')

If

p >

2.

we have

J

$;

~

ffIDUI,,-2ID2UI2(2dxdT

+

'Yp.;~2

fflDU - VI

2

dxdT.

QR(,.) QR(,.)

Putting this estimate in (7.2) proves the lemma in the degenerate case. To estimate

J

in

the singular case 1

<p<

2. we

fU'St

integrate

by

parts

in

the variable

Xi.

This

gives

7.

The perturbation lemma 269

(7.3) J

~

'Y

ffIIDUIP-2DU

-IVIP-2VIID2UI(ID(ldxdT

QIl(,.)

+ f f

II

Du

I

P

-

2

Du

- IVIP-

2

VIIDu

-

VI(ID

2

(ldxdr

QIl(,.)

==Il+h

By

(5.7)

of

Lemma 5.2 and Schwartz inequality

II

~

f

fIDUIP-2ID2UI2(2dxdr

+

i£;~2

f

flDU

-

Vl

2

dxdr,

~W·

~w

and by (5.6)

12

~

'Yp;~2

fflDU -

Vl

2

dxdr.

QIl(")

Combining these estimates in (7.2) proves the Lemma.

Let

8

p

QR/2

(p)

denote the parabolic boundary

of

QR/2

(p).

Consider the

boundary value problem

(7.4)

{

Vi,t

- (IVIP-2

vi

,x;

+

~

-

2)

IVlp-

4

Vt,k

v

i,xlo Vj,i)

Xj

, in Q

R/2

(JL)

Vi

L')pQIl/2(,.)=Ui,

&=

1,2,

...

,m.

The existence

of

a unique solution to (7.4) can be established for example by a

Galerkin

procedureP)

The solution v

==

(vt,

V2,

•••

,

11m)

of

(7.4) is 'regular' in

the interior

of

Q

R/2

(p), in the sense

of

Theorem 6.1. The next lemma compares

U and

v.

LEMMA 7.2.

There

exists a constant

'Y='Y(N,p),

such

thatfor all

0<

p<

R/2

and for every vector V satisfying (5.3),

(7.5) fpDU - Dvl2dxdr

~

'Y

(p_2f!

IDu

-

Vl2dxdr)1I

Qp(")

QIl(")

where

a=mint!;

i}.

f

flDU

-

Vl

2

dxdr,

QIl(")

PROOF:

Write the system (5.1) in the form

!

Ui

- (IVI

P

-

2U

i,Xj +

(p

- 2)IVl

p

-

4

Vt,k

U

i,:t:1o

VjJ)

Xj

=

div

Hi,

i = 1,2,

...

,m,

(1) See Lions

(73).

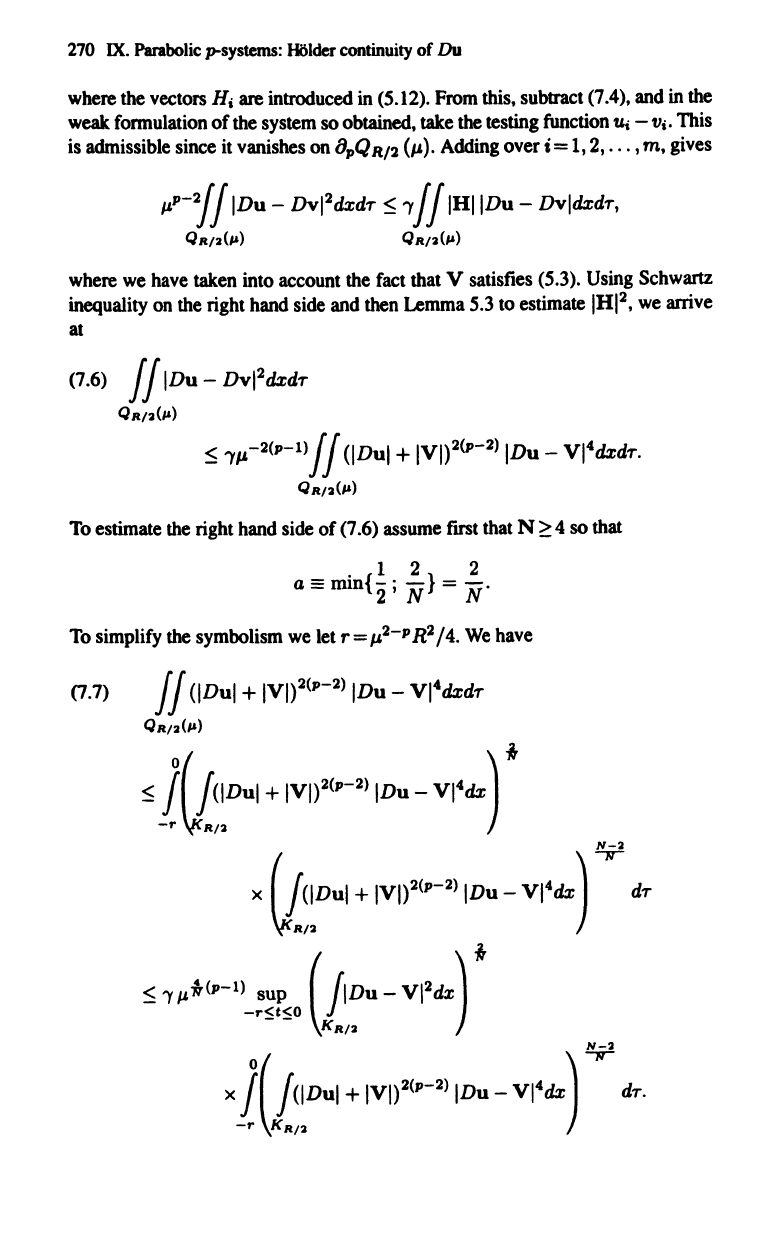
270

IX.

Parabolic

posysterns:

IIUder continuity of

Du

where

the vectors Hi are introduced

in

(S.12).

From

this. subtract

(7.4).

and

in

the

weak

fonnulation of

the

system

so

obtained, take

the

testing

function

Ui

-

Vi.

This

is

admissible since

it

vanishes on

lJ

p

QR/2 ("').

Adding

over

i=

1,

2,

...

, m.

gives

,",p-1/

IDu -

Dvl

2

dxdT

~

..,

//

IHIIDu

- DvldxdT,

QR/2(p)

QR/2(P)

where

we

have

taken

into account

the

fact

that V satisfies

(S.3).

Using

Schwartz

inequality

on

the

right hand

side

and

then

Lemma

S.3

to estimate

IHI2.

we

arrive

at

(7.6) / / IDu -

Dvl

2

dxdT

QR/2(")

~

..,,,,-2(P-l)/ f (IDul +

IVI)2(P-2)

IDu -

V1

4

dxdT.

QR/2(P)

To

estimate the right

hand

side

of (7.6)

assume

first that N

~

4 so that

a =

min{!·

~}

=

~

-

2'

N

N·

To

simplify

the

symbolism

we

let r =

",2-

p

R2

/4.

We

have

(7.7) f f (lDul + IVI)2(p-2) IDu -

VI

4

dxdT

QR/2(P)

"

l(;.~~Du'

+

IVI)'(,,-'l

IDu

_

VI'..,)

i

7.

The

perturbation

lemma

271

By

Lemma

7.1

(7.8)

~*(P-l)

sup

(fIDU

_ V

12

dt)

i

-r<t<O J I

- -

KR/2

To

estimate

the

last factor

in

(7.7)

we

majorise

the

integrand

by

means

of

Lemma

5.1.

It gives

(lDul

+

IVI)2(p-2)

IDu

-

VI

4

= {

(IDuI

+

IVI)

zy!

IDu

_ VI}

4

~

'YIIDulZY!

Du

_IVIZY!vI

4

~

~P~IIDulZY!DU-IVIZY!vl~·

Let x

-+

{(x)

be

a non-negative piecewise smooth cutoff function

in

KR

that

equals

one

on

K

3R

/

4

and

such that

ID{I

~

4/

R.

Then for

a.e.

tE

{-r,

O},

by

the

embedding Corollary

2.1

of

Chap.

I,

we

have

N-2

~

'Y~P¥

(![lIDUIZY!

Du

-IVIZY!VI{]

~

dx)-,;r

K3R/4

~

'Y

~p¥

! ID

[IDulZY!

Du

-IVIZY!V]

{1

2

dx

K3R/4

Here

in

estimating

the

last

term

we

have

used

the

algebraic inequality

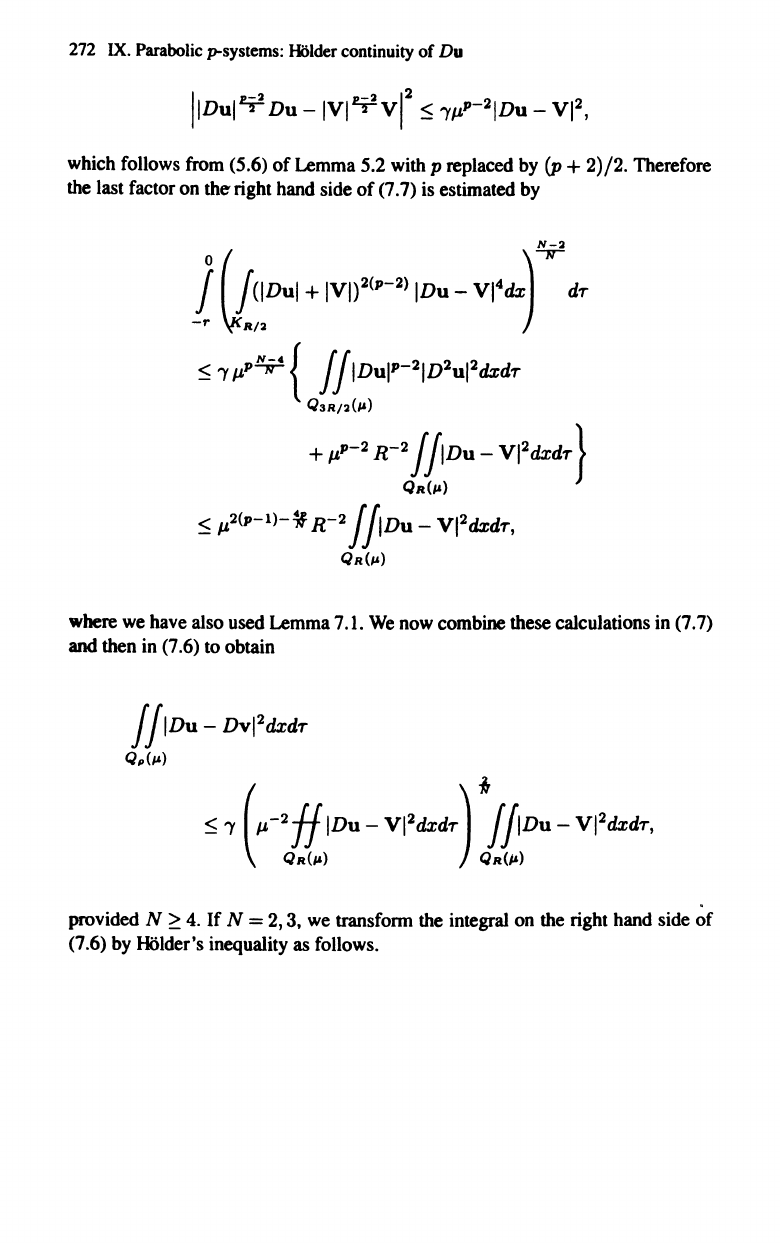
272 IX. Parabolic p-systcms: H5lder continuity

of

Du

which follows from (5.6)

of

Lemma 5.2 with p replaced by (p + 2)/2. Therefore

the last factor

on

the

right hand side

of

(7.7) is estimated

by

N-2

1

V.~~DoI

+

IVI)2lP-2)

IDo

-

VI'.J"

)

-,,-

dT

:5

'Y

I'p~

{

IIIDUIP-2ID2uI2dxdT

Q3R/2("')

+

1'1'-2

R-

2

IIIDU

-

V12dxdT}

QR("')

:5

1'2(1'-1)-11

R-

2

IIIDU

-

V1

2

dxdT,

QR("')

where we have also used Lemma 7.1. We now combine these calculations in (7.7)

and then in (7.6)

to

obtain

IIIDU

-

Dvl2dxdT

QpC",)

provided N

~

4.

If

N = 2, 3, we transform the integral on the right hand side

of

(7.6) by HOlder's inequality as follows.

7.

The perturbation

lemma

273

(7.9) II ODul +

IVn

2

(p-2)

IDu

-

Vl

4

dxd'T

QR/2(")

o

= I

IIDU

-

VI

(IDul +

IVn

2

(p-2)

IDu

-

Vl

3

dxd'T

-rK

R

/

2

1

~

1(l~-V'2dzr

x

(/ODU

'

+ IVI)4(P-2)

IDu

- V

16

dx)

!

d'T

KR/2

~

p.2j! sup

(fIDU

- V

12

dx)

!

-r<t<O

J I

- -

KR/2

1

xl

(J.!;IDuI

+

IVI)'"

IDu

-

vi]'

dz)

·

d.

By Lemma 7.1

We estimate the last

tenn

on the right hand side

of

(7.9) separately for N = 3 and

N=2.

The

case

N=3

Let,

be defined as before. Then for a.e. t E (

-r,

0).

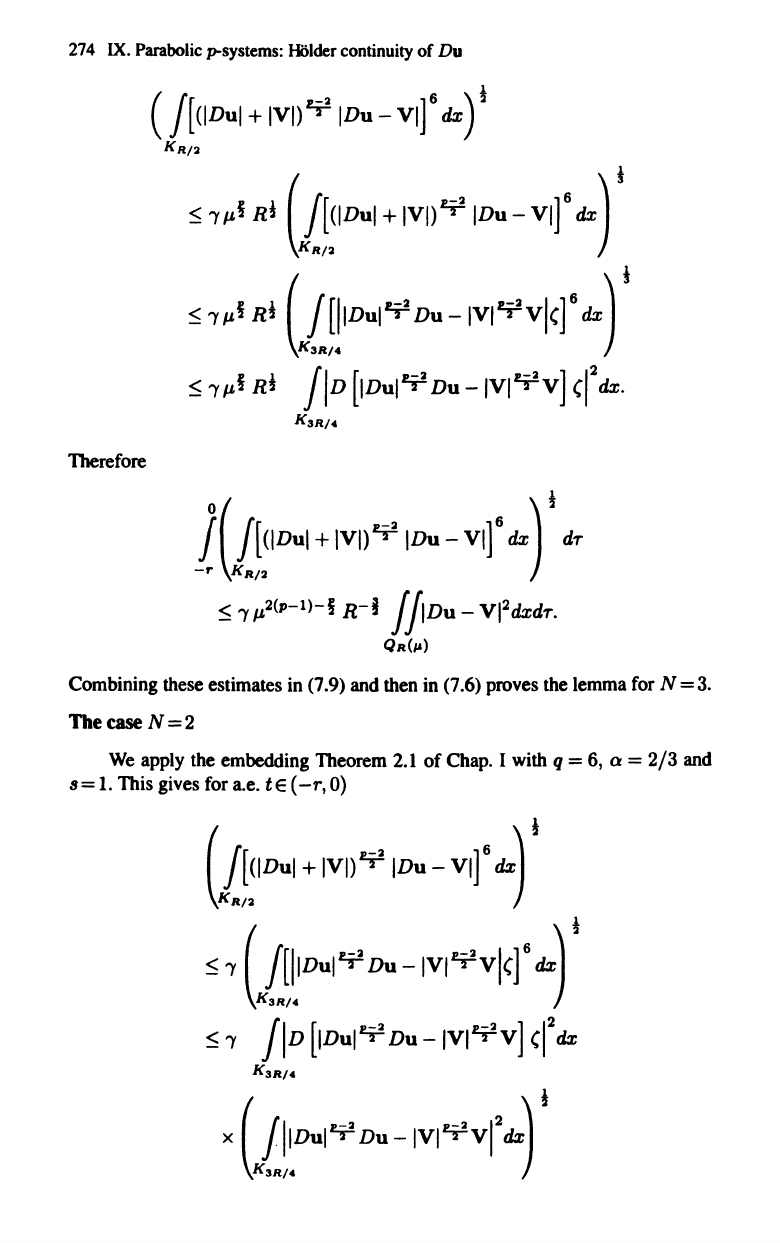
274 IX. Parabolic p-systems: II)lder continuity

of

Du

1berefore

(

J[

(IDul

+

IVI)

E?

IDu

-

Vr

dx ) 1

KR./2

~

'Y

JL

f Rl

(J[

(lDul

+

IVI)

E?

IDu

_

Vf

dx)

1

KR./2

,; 7,,1 RI

(L!!IDuI'i'Du-IVI'i'VI,r

<Ix)

I

~

'Y

JLf

Rl

JID

[IDulE?

Du

-IVIE?V]

'1

2

dx.

K

S

R./4

l(J.!~,Du'

+

IVI)

'i'

IDu

-

Vi]"

<Ix)

I

dT

~

'Y

JL

2

(P-l)-f

R-i

JJIDU

-

V1

2

dxdT.

QR.(")

Combining these estimates in (7.9) and then in (7.6) proves the lemma for N

=3.

TbecaseN=2

We

apply the embedding Theorem 2.1

of

Chap. I with q = 6, Q =

2/3

and

B =

1.

This gives for a.e. t E

(-r,

0)

(

J[(IDuI

+

IVI)'i'IDu

-

Vi]"

J I

KR./2

)

,;

7

(f.~~DuI'T'

Du

-IVI'T'VI'j'

<Ix)

!

~

'Y

JID

[IDulE?

Du

-IVIE?V]

,r

dx

KSR./4

8.

Proof

of

Proposition 1.l-(i)

275

1berefore

l(J.!~IDuI

+

IVI)

"'IDu

-

VI]'

dz

) !

dT

~

'YJLfR

fflD

[IDul~

Du-IVIZY!V]

(r

dxdT

.

QR(")

We

estimate these integrals

by

means

of Lemma

7.1

and

combine the calculations

in

(7.9) and

in

(7.6) to conclude that (7.5) holds

with

a=~.

8.

Proof of Proposition 1.1-(i)

LEMMA

8.1.

There

exist constants

~,

6,

E E (0, 1) that

can

be

determined a priori

only

in

terms

of

N and p.

such

that

ijVo

is

a constant vector

in

R

Nxm

satisfying

(8.1)

(8.2)

HIDU - V

o

l

2

dxdT

~

Ell?,

QR(")

then

there

exists a constant vector V t E R

Nxm

such

that

(8.4)

ffiDU

-V

t

l

2

dxdT

~

~6N+2ffIDU

-V

o

l

2

dt,

Q.R(")

QR(")

(8.5)

HIDU-V

t

I

2

~EIl?

Q.R(")

PROOF:

Let

v be the unique solution

of

(7.4) and set

V t

==

HDvdt,

Q.R(")

where 6 E (0,1) is

to

be chosen. The perturbation

Lemma

7.2 with V = V

o

•

the

triangle inequality and (8.2) give

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.