DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


246
IX.
Parabolic
p-systems:
ltilder
continuity
of Du
lim
inf
'Y
(N, p,
II
Dull
00
K)
,
a-I
(N,p)
-+
00.
p'\,l
'
Remark
1.2. The functional dependence of'Y
upon
IIDulloo,K
will
be
given
in
§§3
and
4.
l-(i).
Some
notation
and
the
two
basic propositions
The proof of Theorem
1.1
is
based
on estimating
the
essential oscillation of
Ui,%j
in
cylindrical domains of the type
[(x
o
,
to)
+ Q
(6,
p)]
c
{IT.
After a trans-
lation
we
may
assume that (x
o
,
to)
coincides with origin. Let
IJ
and
R be positive
numbers
and
consider the cylinders
{
Qn(lJ}
==
Knx
{-1J
2
-
P
R
2
,0}, satisfying
(1.2) sup IDul:5
IJ.
QR(")
The geometry of Qn(lJ)
is
intrinsic
in
that
the
t-dimension
is
'stretched'
by
a
factor, loosely speaking, of
the
order of
IDuI
2
-
p
•
Let
us
assume for
the
moment
that such boxes can
be
constructed. Then Theorem
1.1
is
a consequence of the
following
two
propositions.
PROPOSITION
1.1.
There
exist
numbers
II,
It,
6
in
(0,
1)
that
can
be
determined
a priori only
in
terms
of
N and p.
such
that if
there
holds
(1.4)
//IDU
- (Du)"+l12
dxdr
:5
1t6
N
+
2
/
/IDU
- (Du},,1
2
dxdr,
Q,,,+lR
(,,) Q,,,
R(")
for all
n=
1,2,
...
,
where
(Du)"
= ff
Dudxdr.
Q'''R('')
PROPOSITION
1.2.
There
exists
numbers
j
<u<t']<
1 and
such
that if
there
holds
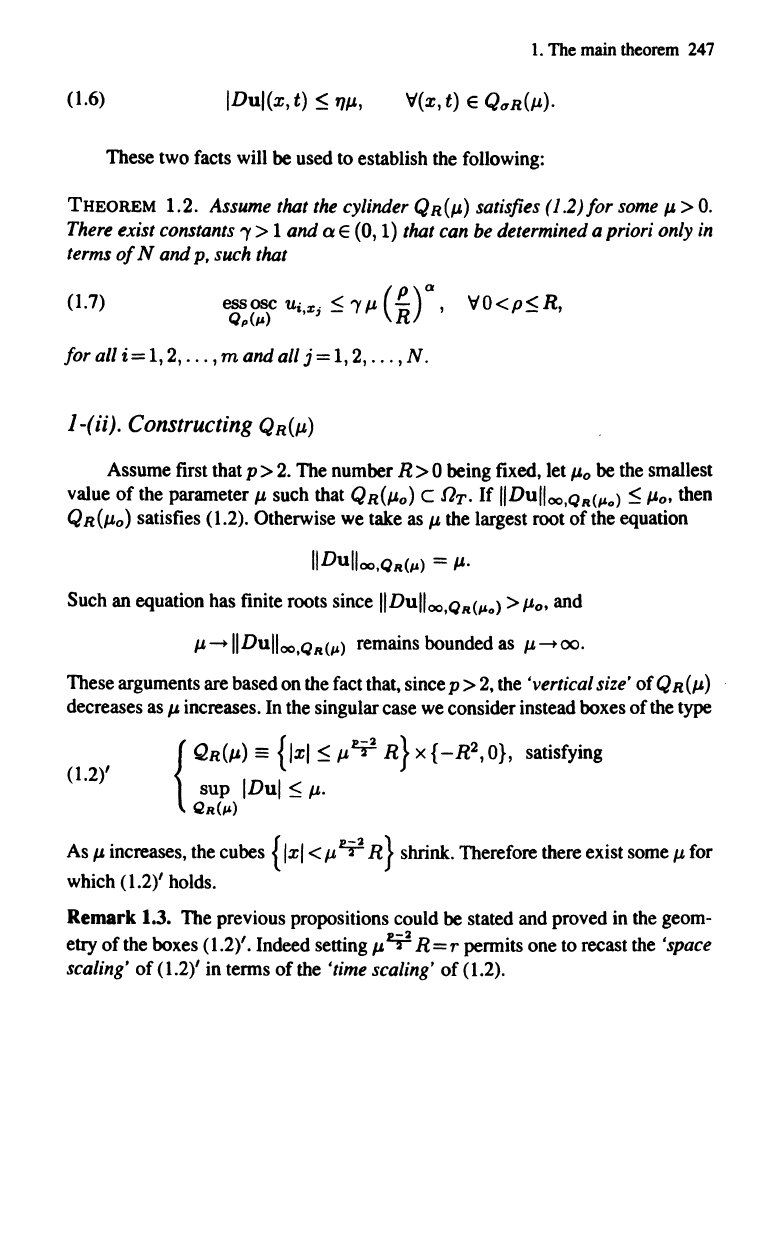
1.
The
main
theorem 247
(1.6)
IDul(x, t)
~
rn~,
These
two
facts will
be
used
to
establish the following:
THEOREM
1.2. Assume that the cylinder Q R
(/J)
satisfies (1.2)
for
some
/J
>
O.
There exist constants "Y> 1
and
a E
(0,
1)
that can be determined a priori only
in
terms
of
N and p, such that
(1.7)
~~
Ui,z;
~
"Y/J
(~r,
VO<p~R,
foralli=1,2,
...
,mandall
j=l,
2,
...
,N.
1-(;;).
Constructing QR(/J)
Assume first that p>
2.
The number
R>
0 being fixed. let
/Jo
be
the
smallest
value of the parameter
/J
such that QR(/Jo) C f1T.
If
IIDulloo,QIlC",o)
~
/Jo.
then
QR(/Jo) satisfies (1.2). Otherwise
we
take
as
/J
the largest root of
the
equation
IIDulloo,QIlC"')
=
/J.
Such
an
equation
has
finite roots since
IIDulloo,QIl("'o)
>
/Jo.
and
/J-IIDulloo,QIlC",)
remains bounded
as
/J-OO.
These arguments
are
based
on
the
fact
that. since p >
2,
the
'vertical size' of Q
R(/J)
decreases
as
/J
increases. In
the
singular case
we
consider instead boxes of
the
type
(1.2)'
{
QR(/J)
==
{Ixl
~
/JP.?
R}
X {_R2,0}, satisfying
sup
IDul
~
/J.
QIl("')
As
/J
increases, the cubes {Ixl <
/J
P.?
R}
shrink. Therefore there exist
some
/J
for
which (1.2)' holds.
Remark 1.3.
The
previous propositions could
be
stated and proved
in the
geom-
etry of the boxes (1.2)'. Indeed setting /JP.?
R=r
permits one
to
recast
the
'space
scaling'
of (1.2)' in terms of
the
'time scaling' of (1.2).

248
IX.
Parabolic
p-systems:
HOlder
continuity of Du
1-(;;i}.
More
about
the
intrinsic geometry
Take formally the
xj-derivative
of
(1.1)
of
Chap. VIII and multiply the
ith
equation
of
the system so obtained. by
'Ui.z
j
'
Adding over i = 1,2,
...
, m and j =
1,2,
...
,N.
and setting w = IDul
2
we arrive at the formal differential inequality
(1.8)
! w - (al,lcw2j!wZk)
Zl
:::; 0 in
nT,
where
(1.9)
at,1c
==
{ 6
t
,1c
+
(p
- 2)
U'j;;:j;Zk
} .
The
matrix
(at,lc)
is positive definite and w is a non-negative weak solution
of
an
equation
of
the porous medium type. This is a parabolic version
of
the
quasi-
subharmonicity.
The degeneracy
of
(1.8) is
of
the order
of
w
2j!
and it is overcome
by
the choice
ofthe
parabolic geometry
of
QR(I-').
2. Estimating the oscillation
of
Du
We
assume Propositions
1.1
and
1.2 for the moment
and
proceed
to prove Theorem
1.1. Let
QR(I-')
be a cylinder satisfying (1.2)
and
define the two sequences
(2.1)
{
1-'0
=
1-',
Ro
= R and for n = 1,2,
...
,
I'n+l
=
TJl'n,
Rn+l
=
CoRn,
where
TJ
and u are the numbers claimed by Proposition 1.2 and
(2.2)
Since
TJ
E (!, 1). we have
Co
E
(0,1)
for all p >
1.
Suppose the assumption (1.5)
holds with
R=Ro and
1'=1'0'
Then
sup
IDul
:::;
TJ
1-'0
==
1-'1'
Q
..
Ro("'o)
From the definitions (2.1) and (2.2) it follows that Rl <
Ro
and
1
'r
0 _ 0
R2 u
2
...J>-2
R2
(U)2
R2
I-'f-
2
=
-4-
TJP-21-'~-2
=
'2
1JP-
2
•
This implies that the cylinder QRl
(I-'d
is contained in
QtTR
o
(1-'0)
and
sup
IDul:::;
1-'1.
QR1(",d
Therefore QRl
(I'd
satisfies (1.2) an4
if
the assumption (1.5)
of
Proposition 1.2 is
verified again for such a box we have

2.
Estimating the oscillation of
Du
249
sup
IDul
~
1-'2.
QR2("1)
Proceeding in this fashion, suppose the assumption
of
Proposition 1.2 is verified
for the cylinders
QR,.
(I-'n),
n =
0,
1,2,
...
,
no
- 1 for some positive integer no·
Then
(2.3)
sup
IDul
~
I-'n
==
'1
n
l-'o,
n =
0,1,2,
...
, no.
QRn
("n)
From the definitions (2.1) and (2.2)
it
follows that
One verifies that
Co
<
'1
for all p >
1,
and consequently
al
E (0,1).
We
rewrite
(2.3) as
(
Rn)Ql
(2.4)
sup
IDul
~
1-'0
D ' for n =
0,
1,2,
...
, no·
QRn("n)
no
Suppose now that the assumption (1.5)
of
Proposition 1.2 fails for no.
We
call
Rno
the
switching
radius.
Then for the box
QRno
(I-'nJ the assumption (1.3)
of
Proposition
1.1
holds and we conclude that
(2.5) H IDu - (DU)i
12
dxdr
~
KiH
IDu - (Du)o
12
dxdr
Q ,iRno
("no
) Q Rno
("no)
<
i 2 . 1 2
_KI-'n
o
'
t=,
, ...
Writing
(2.6) I(Du)i+
1
-
(DU)iI
2
~
21Du -
(DU)i+lr
+ 21Du - (DU)iI
2
and taking the integral average over
Q6i+1Rno(l-'no)
gives
'Y
= 2
(K
+
cS-(N+2»)
.
Therefore {(DU)iheN is a Cauchy sequence whose limit we denote with
Du(
x
o
, to).
To motivate this terminology we recall that our arguments are carried over an ar-
bitrary cylinder
[(x
o
, to)
+
QR(I-')]
with vertex at
(x
o
, to).
Therefore
if
no
is the
switching
radius
of
the box
[(
x
o
, to) + Q R
(1-')],
the limit
ofthe
averages,
HDUdxdr,
[(zo,tO)+Q'iRno
("n
o
)]

250 IX. Parabolic p-systems: flijlder continuity
of
Du
is
Du(x
o
•
to)
for almost all (x
o
•
to)
E n
T
•
It follows from (2.6) that
1 1
2.
2
Du(x
o
•
to)
- (Du),
~
'Y
1t'lJ
no
'
i = 1.2
•....
Fix 0 <
p<
Rn
o
and denote with (Du)p the integral average
of
Du
over Qp(lJnJ.
Let i be a positive integer such that
(2.7)
and estimate
(2.8)
I(DU)p
-
(DU),r
~
ff
IDu -
(DU),r
dxd-r
Qp(""o)
~
'Y6-(N+2)
It'
1J~0'
Therefore
(2.9) IDU(x
o
•
to)
- (DU)pr
~
2IDu(Xo.
to)
-
(DU),r
+
21
(Du)p - (DU),r
~
'Y(
6)
It'
1J~0
.
It follows from (2.7) and (2.9) that
Let
2Q
o
=min{Ql;
Q2}. Then combining (2.9) and (2.4) we conclude
LEMMA
2.1. There exist constants
'Y
> 1 and Q
o
E (0.1) that can be determined
a priori only in terms
0/
Nand
p. such that/or almost all (x
o
•
to)
E
nT
such that
[(xo.
to)
+
QR(IJ)]
c
nT.
and/orallO<p~R.
there holds
(2.10)
Moreover
(2.11)
ff
IDu - (Du)pI2
dxd-r
~
'Y
IJ~
(~)
2
Q
o •
Qp(""o)
Remark
2.1.
The
lemma holds also in the geometry
of
the boxes
[(xo.
to)
+
QR(IJ)]
introduced in (1.2)'. Indeed we may set
1J2j!
R=r
and
work within the cylinder
[(xo.
to)
+
Qr(IJ)].
We arrive at a version
of
(2.10) that reads
(2.10)'

3.
RUder
continuity
of Du (thecasep>2)
251
Returning
to
the
geometry of
[(%0.
to) +
QR(P)]
proves
the
assertion.
Analogous
considerations bold for
(2.11).
3.
HOlder
continuity of
Du
(the case p >
2)
We
assume
that IDul ELOO(n
T
)
and
set
P =
II
Dull
OO,DT
•
This
is
no
loss
of generality.
by
possibly
working
with
another
compact
set
K:,'
satisfying
K:,
C
K:,'
c
nT.
and
dist
(K:,j
K:,')
~
Id.
We
will
prove
the
mlder
continuity of
Du
in
the
time
and
space variables sepa-
rately.
3-(i).
HOlder
continuity
in
t
Fix
two
points
(%0.
t.) E
K:,.
i = 0.1.
with
the
same
'abscissa'
Xo'
We
let
tl
>
to
and
construct
the
cylinders
[(xo.t.) +
QR(P)]
=
{IX
-
xol
<
pEj!
R}
x {t. - R2. t.}.
The
box
[(xo.
h)
+
QR(P)]
intersects
[(xo.
to)
+
QR(P)]
at
the
point
(xo,
to). if
(tl -
to)
<
R2.
Moreover
they
are
contained
in
nT
if
(3.1)
LEMMA
3.1. Let (3.1)
hold.
There
exist constants
'Y
> 1 and Q E (0.1) that
can
be
determined a priori
only
in
terms
0/
Nand
p
such
that/or all pairs (x
o
•
t.) E
K:"
i=O.l.
PROOF:
Let
Rn,
be
the switching radii of the cylinders
[(xo.
ti) +
QR(P)]
and
introduce
the
two boxes
Qi =
[(xo.
t.) + QR", (Pn,)]
=
{Ix
-
x.1
<
PRy
Rn,
} x
{t.
-
R~,.
ttl
.
Assume
first that
(3.3)

252 IX. Parabolic
p-systems:
fm(der
continuity
of
Du
and for i = 0, 1 construct the two cylinders
C
i
==
[(x
o
,
ti) + Q"'2('I-'O) (I'n;)]
=
{IX
-
xol
<
I'!T
J2(tl
-
to)
} X {ti - 2(tl - to),
ti}.
By
virtue of (3.3)
we
have
the
inclusions C
i
C Qi, i = 0,
1.
Moreover
Co
and
C
l
intersect
in
a box satisfying
(3.4)
meas
[Co
n C
l
]
~
min {I'n
o
; Jl.nl}
(tr
- t
o
)(N+2)/2.
Set
(Du)c;
==
H
Dudxdr,
i =
0,
1,
c,
and estimate
IDu(x
o
,
t.)
- Du(xo,
to)1
~
IDu(xo,
tl)
-
(DU)Cl
1
+ IDu(x
o
,
to)
- (Du)C
o
1
+ 1
(DU)Cl
-
(Du)c
o
I·
By (2.10)
and
Remark.
2.1
we
have, for
i=O,
1,
To
estimate the last term
we
add and subtract Du(x, t) where (x, t) E
Co
n C
l
,
and
then take
the
integral average over such intersection, i.e.,
I
(Du)c
o
-
(Du)c
o
1
~
HI
(Du)C
1
-
Du(x, t)ldxdr
C
o
nel
+ H IDu(x, t)
-.
(Du)c.l
dt
.
C
o
nel
Without loss of generality
we
may assume that min {I'noj I'nl } =
I'nl.
Then
we
estimate
the
first integral
by
extending
the
integration over the larger set Cl. Taking
into account
the
definition of C
l
,
(3.4) and (2.11),
we
obtain
HI
(DU)Cl
- Du(x,
t)1
dxdr
~
'Y
HI
(DU)Cl
- Du(x,
t)1
dxdr
C
o
nel
Cl
(
~)QO
~'YI'
R
To
estimate the second integral, let
fJ
be
a small positive number
to
be
chosen
and
assume that

3 .
.Hl)lder
continuity
of
Du
(the
case
p>
2)
253
(3.5)
Then using again (2.11) and (3.4),
H IDu(x, t) - (Du)c
o
Idt
Conel
(
)
N(P-2)/2H
:5
"I
~::
IDu(x, t) - (Du)C
o
Idt
Co
< (I-'n
o
)N(P-2)/2
(~)QO
- "I
#Jnl
I-'
R
<
V(tt
-
to)
( )
Qo-{JN(p-2)/2
-"II-'
R
Therefore if (3.3) and (3.5) hold,
the
assertion (3.2) follows by taking
{3
=
Q
o
/ N (p - 2)
and
then choosing Q = Qo/2.
If
(3.5)
is
violated,
(
~)
Q
o
/N(p-2)
IDu(x
o
,
to)
- DU(Xl, tdl
:5
21-'
R 0 ,
and
the
assertion follows
by
suitably modifying the defmition of
Q.
We
consider next the case
when
(3.3)
is
violated, i.e.,
2(tl -
to)
> min {R!o j
R!l}'
If
R!,
:5
2(tl -
to)
for
i=O,
1, then by (2.4)
I
I
(
v'fl=t;;)
Q
Du(x
o
,
tt)
-
Du(x
o
,
to)
:5
I-'no
+
I-'nl
:5
"II-'
R
Therefore
we
may
assume that,
say,
R!l
:5
2(tt
-
to)
<
R!o'
We
conclude the proof by reducing this case to the situation (3.3). Let
n.
:5
nl
be
a positive integer satisfying
R!.
~
2(tl -
to)
~
R!.+l'
and introduce the cylinders
Qo
and (2., where
Q.
==
(xo, ttl +
QR".
(I-'n.)
==
{Ix
-
xol
<
I-':f
Rn.
} x {tl -
R!.,tl}'
Since
we
have
2(h -
to)
:5
min {R!o j
R!J,
the box Q
..
will now play the same role
as
the cylinder
Ql
in the
case (3.3). The
proof
is
now
concluded
as
before, observing that for Q
..
the
two inequalities (2.10)
and (2.11) hold true.

2S4
IX.
Parabolic
p-systems:
H6lder
continuity
of
Du
LEMMA
3.1'.
There
exist
constants
1>
1 and Q e (0, 1) that
can
be
determined a
priori
only
in
terms
of
N andpsuch thatforevery pair
of
points
(Xi,
to)
elC,
i=
0,1,
PROOF:
If
JI.'~
1
we
take
R=dist
(lC;r)
in
(3.1).
Otherwise
we
take
IJ¥
R=
dist
(IC;
r).
3-(U).
Holder continuity
in
x
Fix
two
points
(xo,
to)
and
(Xl,
to)
in
K..
at
the
same
time
level
to.
and
let
[(Xi,
to)
+
QR{IJ)]
==
{Ix
- xii <
R}
x
{to
-1J
2
-
P
Jtl,
to},
i =
0,1,
be
two
boxes
satisfying (1.2).
The
box
[(xo,
to) +
QR(P)]
will
intersect
Xl
iflxo-
xII < R. Moreover
they
are
contained
in
n
T
if
(3.6)
LEMMA
3.2. Let (3.6)
hold.
Thereexistconstants1> 1
andQE
(0,
1)
that
can
be
determined a priori only
in
terms
of
Nand
p,
such
thatfor all
(Xi,
to)
E
K.,
i = 0, 1,
(3.7)
IDU(XI,
to) - Du(x
o
,
to)
I $
11J
(Ixo
~
XII) Q •
PROOF:
Let
R.n..
be
the
switching
radii
corresponding
to
the
two
boxes
[(Xi,
to) +
QR(IJ)]
,
and
construct the
two
cylinders
. Qi
==
[(Xi,
to) + QR.., (IJ",)]
==
{Ix
- xii <
R.n.,}
x {to -IJ!;-P
R!"
to} .
Consider separately
the
following
two
cases:
(3.8)
(3.8)'
If
(3.8)
holds,
construct
the
two
boxes
C
i
==
[(Xi,
to) +
Q21Zo-Z11
(J.'n.)]
==
{Ix
- xii <
21xo
-
XII}
x
{to
-1J!;-P4Ixo - xll2, to}.
By
construction these
are
contained
in
Qi
and
they
overlap
in
a
box
satisfying

Set
and estimate
3.
ltilder continuity
of
Du
(the case
p>
2)
255
(Du)c,
==
if Dudt,
c,
IDu(Xt.
to)
- Du(x
o
,
to)1
:5;
IDu(xI,
to)
-
(DU)Cl
I
+ I Du(xo,
to)
- (Du)c
o
I
+ I
(DU)Cl
- (Du)c
o
I·
The proof now proceeds as for the HOlder continuity in t with minor cbanges.
LEMMA 3.2'. Thereexistconstants'Y> 1 andQE (0, 1) that
can
be
determined a
priori only
in
terms
of
N and p
such
that for every pair
of
points
(Xi,
to)
E
/C,
i =
0,1.
PROOF:
If
JJ
~
1. in (3.6) we take R =
dist
(/C;
r).
If
JJ
<
I,
we take R =
JJ2.f!
dist
(/C;
r).
Then (3.7) reads
(3.7)'
If
2.f!
Xl
-
Xo
(
I I
)
0/2
JJ
:5;
dist
(/C;
r)
,
there is nothing
to
prove. Otherwise (3,7)' gives
Thus (3.10) follows by suitably redefining the number
Q.
3-(iii). A version
of
Theorem
1.1
Combining Lemmas
3.1'
and 3.2' gives the following form
of
Theorem 1.1:
