DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


226
vm.
Degenerate
and
singular
parabolic
systems
The discrete derivative
of
(2.6)', with respect
to
Xj,
takes the fonn
(3.9)
~6
·U·
h - div
[6
·IDuI
P
-
2
Du·] = 0
at
'
I,
, I h '
i =
1,2,
...
,m,
a.e. 0
1
'71
x
(O,T
- h).
In
transforming the term
[6
j
IDulp-
2Du
i],
we only specify the Xj variable for
simplicity
of
symbolism. We have
(3.10) 6
j
lDulp-2
DUi
1
=
~!
d~
{luDu(Xj +,,) +
(1
- U)DU(Xj)r-
2
o
x
(UDUi(Xj
+
71)
+
(1-
U)DUi(Xj»)}du
1
=
D6jUi
! luDu(Xj +
71)
+
(1
- u)DU(Xj)I
P
-
2
du
o
1
+(p - 2)6jUl,Z.!luDu(Xj +
71)
+
(1-
u)DU(Xj)I
P
-
4
o
x
(UUl,Z/c(Xj
+
71)
+
(1-
U)UI,z/c(Xj»)
x
(UDUi(Xj
+,,) +
(1-
u)DUi(Xj»)du.
To simplify the symbolism we let
~P)
(u) denote the
N-dimensional
vector
~P)(u)
=
UDUi(Xj
+
71)
+
(1-
U)DUi(Xj)
and let
~
(j)
(u) be the N x m matrix
~(j)(u)
=
uDu(xj
+,,) +
(1
-
u)Du(xj).
Having fixed the point (xo,
to)
E OT, if!(xo,
to)
+ Q (9,
p)]
c OT we may assume,
up to a translation, that
(xo,
to)
coincides with the origin, and then by choosing
1711
and h sufficiently small we may assume that Q (9,
p)
c 0
1
'71
x
(0,
T - h). We
multiply (3.9) by the testing function
where,
is a standard non-negative cutoff function that vanishes on the boundary
of
K
p'
We integrate over (
-9,
t) for arbitrary
-9
< t
~
0, and add over i = 1, 2,
...
, m
and j
= 1, 2,
...
,
N.
This gives

3.
Weak
differentiability of
IDul~
Du
and
energy
estimates for
IDul
227
/.(t
..
;/(S)u)
,'(.,t)dz
~.
t
+ I I
[CjI
Du
l,,-2
DUi]
h . DCjUi,hl
(l
c5u
hl)
(2dxdr
-9K
p
t
+ I I
[c5
j
I
Du
l,,-2
DUi]h
·c5
j
U
i,h
D
I
(l
c5u
hl)
(2dxdr
-9K
p
t
=
-2
I I
[c5
j
I
Du
l,,-2
DUi]
h
·c5jUi,hl
(lc5
u
hl)
(D(
dxdr
-9K
p
In
this equality
we
first let
h'--+
0,
while
I'll
> 0 remains
fixed.
The various
limits
are
justified since IDul eLfoc(nT)
and
ueC,
oc
(0, T;Lfoc(n»).
Making
use
also
of
(3.10)
we
obtain
(
16
1 ) t
(3.11) sup I r U
sl(s)
ds
(2(x,
t) dx
-9<t<O
Jo
9
Kp -
+
II
(foia(j)
(u)I,,-2dtr )
ID6
j
U
l
2/
(16ul)(2dxdr
Q(9,p)
+(p
-
2)
II
(folla(j)(U)I,,-4Ia(j)(U).Dc5jUI2dtr ) I
(16ul)
(2dxdr
Q(9,p)
+
II
(foia(j)
(u)I,,-2du )
IDI6ufl
6u
Il'
(l6ul) (2dxdr
Q(9.p)
+(p
-
2)
II
(foia(j)(u)I"-4a(j)(U).D6jUa~j)(U)6jUidU)
Q(9,p)
x D16ulf' (l6ul) (2dxdr
~
2(P - 1)
II
(foia(j)
(u)I,,-2dtr )
IDc5
j
U
II
c5u
l I
(16ul)
(ID(ldxdr
Q(9.p)
+2
II(foI6~1/(S)dS)
"tdxdr.
Q(9.p)

228
VID.
Degenerate
and
singular parabolic systems
First we observe that the sum
of
the
fmt
two integrals over Q
«(J,
p)
on the left
hand side, is bounded below by
min{Ij
(P
-I)}
ff
(foi
J1
(;)
(U)I
P
-
2
d,q)
ID6;u1
2
f
(16ul)
(2dxdr.
Q(9,p)
If
p > 2, this is obtained by discarding the coefficient (p - 2).
If
1<
P < 2, we
estimate below
(p
-
2)
ff
(111J1(;)(U)IP-41J1(;)(U).D6;uI2
d,q
) f
(16ul)
(2dxdr
Q(9,p)
2!
(p - 2)
ff
(Li
J1
(j)
(u)IP-2d,q )
ID6;ur
f (l6ul) (2dxdr.
Q(8,p)
Next by Young's inequality, for all e > 0,
ff
(l
iJ1
(j)
(u)IP-2d,q )
ID6;u11
6u
l
f (l6ul)
(ID(I
dxdr
Q(8,p)
$ e
ff
(liJ1(;)
(u)
IP-2d,q
)
ID6;u1
2
f (l6ul) (2dxdr
Q(9,p)
+
'YE
ff
(l
iJ1
(;)
(u)I
P
-
2
d,q
)
16ul
2
f (l6ul)
ID(1
2
dxdr.
Q(9,p)
These remarks in
(3.11)
give the integral inequality involving discrete derivatives

3.
Weak
differentiability
of
IDul1j!
Du
and
energy estimates
for
IDul
229
(3.12) sup
I(
fI6~f(s)
dS)
(2(x,
t) dx t
-9<t<0
10
9
Kp -
+ [min{I;
(p
-I)}
-
e)
II
(l
iil
(j)
(a)IP-2d,q
)
Q(9,p)
x
ID6jUl2
f
(16ul)
(2dxd-r
+
II
(l
iil
(i)
(a)IP-2d,q
)
IDl6ufl6ulf'
(l6ul) (2dxd-r
Q(9,p)
+(p -
2)
II
(l
iil
(j)
(a)IP-4
(il(i)(a).D6
j
u)
.1~j)(a)6jUid,q)
Q(9,p)
x DI6ull'
(16ul)
(2dxd-r
5')'
II
(l
i
.1(i)
(a)IP-2d,q
)
16ul
2
f
(16ul)
ID(1
2
dxd-r
Q(9,p)
+7
JJ
(l"'1
f
(8)d}C,
dxd7,
Q(9,p)
for a constant ,),=,),(p, e).
3-(ii).
Weak
differentiability
oflDullj!ui,zi
In (3.12) take f
==
1 and select a cutoff function that vanishes
on
the parabolic
boundary
of
Q
(0,
pl.
In particular,
(.,
-0)
=
O.
We discard the first
tenn
and
observe that the integrand in the remaining integral on the right hand side is non-
negative. Therefore
letting"
- 0 with the aid
of
Patou's Lemma gives
(3.13) II vP-2ID2UI2,2dxd-r 5
')'
II (vPID(/2 + v
2
((t)
dxd-r
Q~~ ~~~
for a constant')' =
')'(P).
If
p > 2, the inequality (3.1) follows from (3.13) by
choosing
(,
a cutoff function that equals one
on
Q (
aO,
a
p)
and such that
1
ID(/5
(1
- alp'
1
05
(t
5
(1-
a)O·
To prove (3.3) for the singular case, we transfonn the last integral in (3.13) by
means
of
an integration
by
parts as follows.
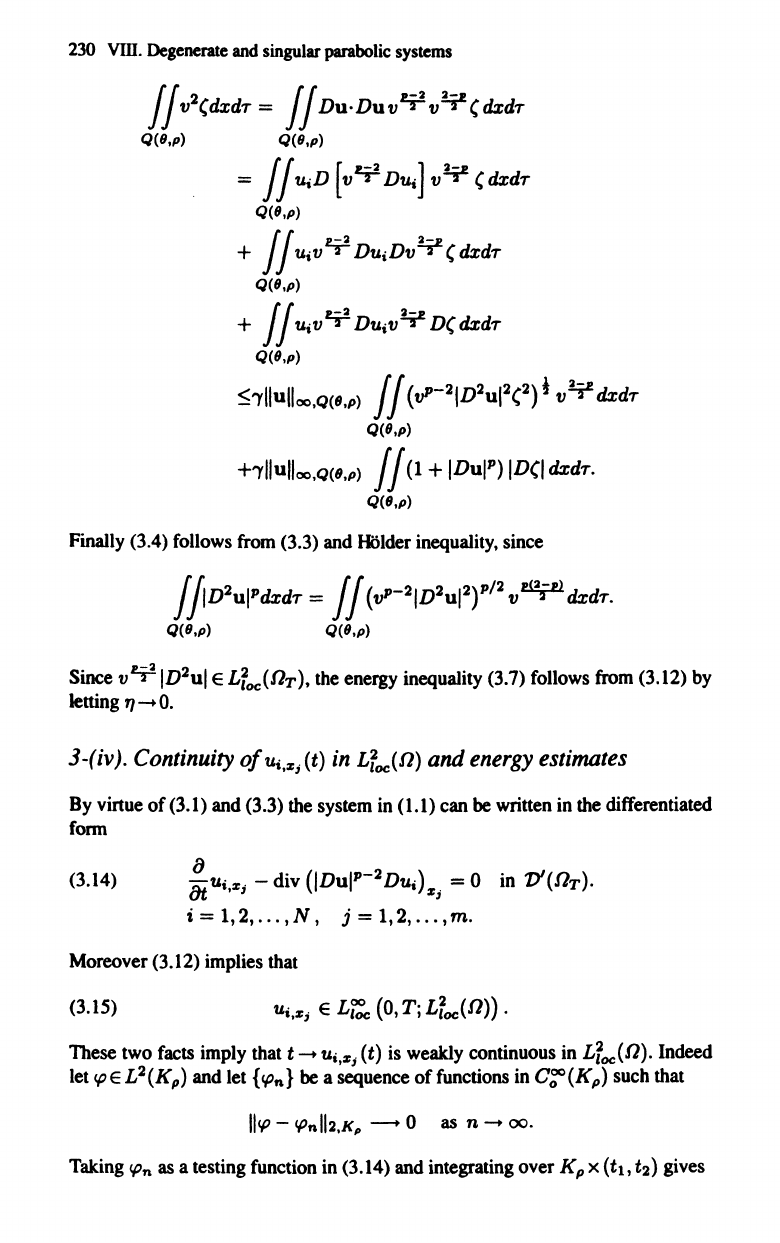
230
vm.
Degenerate
and singular parabolic
systems
IIv
2C
dxdT
=
II
Du.Duv1!j!
v
!TCdxdT
Q(9,p) Q(9,p)
=
II
UiD
[v2:f1
DUi]
v!T
CdxdT
Q(9,p)
+
II
UiVEj!
DUiDv!jR
C
dxdT
Q(9,p)
+
II
UiVEj!
DUiv!jR
DC
dxdT
Q(9,p)
~'Yllulloo,Q(9,p)
II
(vP-2ID2uI2C2)
t v!jR
dxdT
Q(9,p)
+'Yll
u
ll
oo
,Q(9,p)
I I (I + IDuI
P
)
IDCI
dxdT.
Q(9,p)
Finally (3.4) follows from (3.3) and RUder inequality, since
lfiD2ulPdxdT
=
II(vP-2ID2uI2)P/2v~dxdT.
Q(9,p) Q(9,p)
Since v1!j!
ID
2
uI
E
L~oc(nT).
the energy inequality (3.7) follows from (3.12)
by
letting
'1--+0.
3-(iv).
Continuity
of
Ui,:I:;(t)
in
L~oc(n)
and
energy
estimates
By
virtue
of
(3.1) and (3.3) the system
in
(1.1) can
be
written in the differentiated
fonn
(3.14)
!!.U· - div (IDuIP-2
Duo)
= 0 in 1J'(flT)'
&t
1,:1:;
1
:t&;
i = 1,2,
...
,N,
j = 1,2,
...
,m.
Moreover (3.12) implies that
(3.15)
These two facts imply that
t
--+
Ui,:t&;
(t)
is
weakly continuous in
L~oc(n).
Indeed
let
cP
E
L2
(K
p)
and let
{'Pn}
be
a sequence
of
functions
in
C~
(K
p)
such that
IIcp
-
'Pnll2,K
p
--+
0
as
n --+
00.
Taking
CPn
as
a testing function in (3.14)
and
integrating over
Kp
x
(tl,
t2)
gives

4. Boundedness
of
IDul.
Qualitative estimates
231
t3
j
[Ui,z;(t2)
- ui,z;(td]
cp,.dx
= j j (IDul,,-2Dui) Dcp,.,z;dxdr
Kp
tlKp
for almost all
-0
<
tt
<
t2
$
O.
Therefore
lim
sup
j[Ui,Zj
(t2)
-
Ui,zj
(tt)]
cp,.
dx =
O.
I
t
3-
t
d-..o
Kp
From this and (3.15)
lim
sup
I j[Ui,Zj(t2) - Ui,Zj(tt)]
CPdxl
I
t
3-
t
d-..o
Kp
$
limsup
j
[Ui,Zj(t2)
- Ui,zj(td]
cp,.dx
I
t
3-
t
lf-<O
Kp
+ 2
sup
lIui,z;
112,K
p
(t)IIcp
-
cp,.II2,K
p
.
-8~t~O
To prove that
Ui,z;
is strongly continuous in
L~oc({J)
it suffices to prove that
(3.16)
limsup
(IIUi,z;(1I2,Kp(t2)
-IIUi,z;(1I2,Kp(td)
-.0,
I
t
2-
t
lf-<O
where
(is
a piecewise smooth cutofffunctions in Kp vanishing on
oK
p
.
In (3.14)
take the testing function
and integrate over
Kp x
(tl'
t2). By calculations similar to those leading to (3.12)
we obtain
I f
[.'(")
-
.'('1)
I
"<hI
Kp
4. Boundedness
of
I Dul. Qualitative estimates
Using the weak differentiability
of
IDul¥Ui,z;
we first prove that
IDul
is in
Lroc
(fh)
for all q
~
1.
If
K.o
C
K.I
are compact subsets
of
fh,
we will show that
the norm
IIDullq,K:
o
is bounded only in terms
of
q,dist{K.o;K.tl
and the norm

232
vm.
Degenerate
and singular parabolic
systems
IIDullp,K:l.
We
will do this in a qualitative way and with no precise specification
of
the functional dependence.
We
will use such qualitative infonnation to prove
still
qualitatively that
/Du/
E
Ll:
c
{!1
T
),
with bounds only dependent on local
V-nonns
of
/Du/.
Finally, in
the
next section, we will tum such qualitative in-
fonnation into precise
quantitative estimates
of
IIDulloo,K:
o
over compact subsets
lCoc{h.
LEMMA
4.1. Let u be a local weak solution of(1.1). Moreover in the singular
case
1 < p < 2 let the approximation assumption (1.9) be in force. Then
/Du/
E Lloc{{h),
forevery
q E [1,00).
PROOF:
Consider first the degenerate case p >
2.
Let Q
(6,
p)
c
{h
and let (
be a standard non-negative cutoff function vanishing
on
the parabolic boundary
of
Q
(6,
p). Thus, in particular,
(.,
-6)
=0.
In (3.7), take J(v)
=v
P
,
where
P?O
is
to
be chosen. Proceeding fonnally we obtain
(4.1)
sup
Iv
2
+
pe
(x,
t)dx
$
'Y
jr
f
(1
+
vP+
lt
)
dxdr
-9<t<O
J
- -
Kp
. Q(9,p)
o
(4.2)
IIIDv£¥r
dxdr
$
'Y
II
(1
+
vP+
P
) dxdT,
-9K
p
Q(9,p)
where
'Y
=
'Y
(N,p,
p,
(t,
D().
These are rigorous
if
the right hand side is finite.
We
apply the embedding Theorem 2.1
of
Chap. I to the functions
x
-+
(v£¥()
(x, t), a.e. t E
(-6,0),
over the cubes Kp. It suffices to consider the case N >
2.
Indeed
if
N = 1,
2,
we
may consider
u as a vector field defmed in
RN
N ? 3, up to a localisation, and
deduce inequalities
(4.1 )-(4.2) for it. Let 6 be a positive number to
be
chosen. Then
by Corollary
2.1
of
Chap. I and HOlder's inequality
We integrate over
(-6,0),
to obtain

4. Boundedness
of
IDuI.
Qualitative estimates 233
J J
....
•
..
"dzdT
$
JJIv.'¥
'I'
dzdT
C:~r<o
J
.'If
,'(x,
t)J
1N
Q(8.p) Q(8.p)
~
- -
Kp
J
Choosing 6 =
2¥1
and combining this with (4.1)-(4.2) gives the recursive in-
equalities
(4.3) I I
tr.8~+i
(2dxdr
:5
'Y
11(1
+
vJ'+.8)
dxdr,
Q(8.p) Q(8.p)
for a constant
'Y
=
'Y(N,p,/3,(t,D().
The right hand side is finite for
/3
=
o.
Therefore
IDul
E
Lr;4/N
({IT). We may now again apply (4.3) with
/3
=
4/N
and
proceed in this fashion to prove the lemma.
We now
tum
to the singular case 1 < p < 2. In (3.7) assume that
(x
o
,
to)
==
(0,0) and choose a cutoff function ( that vanishes
on
the parabolic boundary
of
Q
«(J,
p).
Take also f (
v)
=
v.8,
where
/3
~
0 is
to
be chosen.
By
working with
the approximations claimed
by
(1.9) we will use the qualitative infonnation that
IDul
E
L~oc(nT).
Our
estimates however will
be
only in tenns
of
IIDull".Q(8.p).
Proceeding fonnally we obtain from (3.7)
(4.4)
Illvl!.±f=.!
D
2
U(r
dxdr
:5
-y
{
II
tr.8dxdr +
II
V
2
+.8(dxdr}
,
Q(8.p) Q(8.p) Q(8.p)
where
-y=-y
(N,p,
{3,
(t,
D().
Also by a fonnal integration
by
parts
/lv.8+
2
(dxdr
=
//V~+f-2
Du.DuvP+~-P(dxdr
Q(8.p) Q(8.p)
=
IluD(V~DU)
v~(dxdr
Q(8.p)
+ / / u
vP.±f=!
Du
Dv~
(
dxdr
Q(8.p)
+
II
u
vP.±f=!
Du
v~
D(
dxdr
Q(8.p)
:5
'Yllulloo.Q(8.p)
/
/l
v
l!.±f=3
D2ul(
v~
dxdr
Q(8.p)
+
'Yll
u
ll
oo
.Q(8.p)
II
v.8+1
dxdr.
Q(8.p)
We combine this with (4.4) and make use
of
the Schwartz inequality to arrive at

234
vm.
Degenerate
and singular
parabolic
systems
(4.5) J J v
P
+
2
(dxdT
~
'Y
J /
(1
+
vf3+(2-p)
+ vf3+l) dxdT,
Q(6,p) Q(6,p)
for a constant
'Y='Y (N,p,
{j,
(t,
D(,
lIulloo,Q(6,p»)
.
This inequality
is
indeed rigorous as long
as
the
right hand side
is
fmite.
We
apply it
fIrSt
with
(j
=
p-l
to deduce that IDul E
L~l
(n
T
).
with bounds only dependent on
II
Dullp,Q(fI,p)
. Then we apply it again with
{j
= p
to
deduce that IDul E
L~2
(nT
).
Proceeding this way proves the lemma.
,
LEMMA
4.2.
Let u be a local weak solution of(1.1). Moreover in the singular
case
1 < p < 2 let the approximation assumption (1.9) be in force. Then
PROOF:
Consider first the degenerate case
p>
2.
Let Q (6,
p)
c n
T
and let
Qn
and
Qn
be
the family
of
cylinders introduced in (2.9)-(2.12). Let also k
n
and
(n
be
respectively the increasing levels defined
in
(2.13) and the cutoff functions
in
Qn
introduced
in
(2.14).
We
put these choices in the energy estimates (3.7) and
as
a function f ( v) take
f(v)
::
(v -
kn+l)r
2
•
By
virtue
of
Lemma
4.1
and Corollary 3.1. such a choice
is
admissible. The tenn
involving D
2
u
is
estimated below
by
II
v"-
2
ID
2
uI
2
f(v)(2dxdT
~
(~)P-'l/ID
(v -
kn+l)!
12
(!dxdT.
Qn
On
1bese choices yield the inequalities
(4.6)
-fl:{:~O
/[(v-k
nH
)l(n]\x,t)dx
KPn
+ k
P
-
2
//ID
[(v - k
n
+1)l
(n]12
dxdT
Qn
~
(12!;2p2
J J
,,2(P-l)'X,[(V
- kn+l)+>0] dxdT
On
for a constant 'Y='Y(N,p).
To
simplify the symbolism let
us
set
(4.7)
Yn ::
/1("-kn)~dXdT.
Qn

4.
Bc..undedness
of
IDul.
Qualitative
estimates
235
Then
we
have(l)
(4.8) / /
X[(v
- kn+l)+>
0]
dxdr
~
'Y
2k7
/ /
(v
-
kn)~
dxdr
Qn
Qn
==
'Y2np
k
-p
Y
n
.
By
Proposition
3.1
of
Chap.
I
with
m=p
- 2
and
q=
2(N
+
2)/
N.
(4.9)
Y
n
+
1
~
/
/[(V
- kn+d,:/2
(nr
dxdr
Qn
$
(tfi
(-
-
k.
H
)'."
(.]'''#
dxdT)
w'h
x
(if
>IJ-
- "-+1)+>
oJ
dxdT)
.to
~
(1'Y~:)2
k-~Yn~
{p-2
//
V
2
(P-I)x[(V
-
kn+l)+>O]
dxdr
Qn
+
(J-I
//vPX[(v - kn+l)+>
0]
dxdr}
I
Qn
where.\2
==
N(P -
2)
+
2p.
These
are
the
key
recursive inequalities
needed
to
derive a quantitative sup-bound
for
IDul.
We
will
use
them
first
in
a qualitative
way
as
follows.
First let A denote a
lump
constant depending
upon
(J
I
(I,
P
and
the
quantities
IIDuIl2,Q(B,p)
II
Dullq,Q(B,p)
q =
(N
+
2)(P
-
2)
+ p.
Then
we
estimate
/ / v
2
(p-I)X[(v - kn+l)+>O]
dxdr
Qn
= / /
vwhvP~x[(v
- kn+d+>
0]
dxdr
Qn
(I)
See §7-(i) of Chap. V
and,
in particular, estimate (7.2).
