DiBenedetto E. Degenerate Parabolic Equations

256 IX. Parabolic p-systerns: Holder continuity

of

Du

THEOREM

1.1'

(THE

DEGENERATE

CASE

p>

2). Let u be a weak solu-

tion in

n

T

of

the degenerate system (1.1)

of

Chap. VIII, and assume that

I-'

=

IIDulloo.o

T

<

00.

There exist constants

'Y

> 1 and Q E (0,1) that can

be

deter-

mined a priori only in terms

of

Nand

p such that, for every compact subset

fC

of

n

T

•

(1.1')

IDu(x

o

,

to)

-

Du(xl.

t

1

)1

<

(Ixo

-

Xli

+ max{I;I-'2j!}v'lt

o

-

t11)0<

-

'YI-'

dist

(fC;

r)

,

for every pair

of

points

(Xi,

til E

fc,

i=O,

1.

Remark

3.1. The constants

'Y

and Q are independent

of

dist

(fc;

r)

and

1-'.

The fonn

of

(1.1)' suggest we reduce the system (1.1)

of

Chap. VIII to another

for which

I-'

=

1.

Introduce the change

of

variables

Ui

. 2

Vi

==

-,

t = 1, ,

...

,m,

IJ.

and T = tl-'p-2.

Vt

- div IDvl

p

-

2

Dv

=

0,

in

nT

==

nx

(0,

T I-'p-2) ,

and

IIDvll

~

=

1.

We

write (1.1)' for v in the variables (x,

T)

and return to the

oo,~6T

original coordinates. This gives

for all pairs

(Xi,

til E

fC,

i

=0,

I,

where

IJ.

-

dist

(fc;

r)

==

inf

(Ix

-

yl

+

1J.2j!~)

(

..

,tIEIC

(v,-IET

is the intrinsic parabolic distance from

fc

to

r.

4.

HOlder

continuity of

Du

(the case 1

<p<

2)

In the singular case 1 < p < 2, the role

of

the parabolic geometry is reversed. As

before, we investigate separately the HOlder continuity in

the space and in the t,

variables. The arguments are similar to those in the degenerate case and we only

indicate the main differences.

4.

Hl)lder

continuity

of

Du

(the case I < p <

2)

257

4-0). Holder continuity in t

Fix two points

(xo,

til E

J("

i = 0,

I,

with the same 'abscissa'

Xo.

We let

tl

>

to

and construct the cylinders

[(Xo,

ti) +

QR(I-')]

==

{Ix -

xol

< I-'Ej!

R}

X {ti - R

2

,ti}'

i = 0,1.

The box

[(xo,

t

l

)

+

QR(I-')]

intersects

[(xo,

to)

+

QR(I-')]

if

(h

-to)

<

R2.

More-

over they are contained in

flT

if

(4.1)

max {1-'2jl R;

R}

:$:

dist (J(,j

r)

.

Proceeding as in the case

p>

2 we have

LEMMA

4.1. Let (4.1)

hold. There

exist constants

'Y

> 1 and a E (0,1) that

can

be

determined a priori only

in

terms

of

N and p

such

that

1-'?I, we take

R=d

in (4.1), and

if

1-'<

I,

we rewrite (4.2) as

(4.2)'

Arguing as in the proof

of

lemma 3.2' and bY.possibly redefining the constants

'Y

and

a,

we obtain

LEMMA

4.1'.

There

exist constants

'Y

> 1 and a E (0,1) that

can

be

determined

a

priori only

in

terms

of

Nand

p

such

that for every pair

of

points

(xo,

ti) E

J("

i =

0,

I,

4-0i).

HOlder

continuity

in

x

Fix two points

(xo,

to)

and

(Xl,

to)

in

J("

at the same time level

to,

and let

[(Xi,

to)

+

QR(I-')]

==

{Ix

-

Xii

< R} x

{to

-1-'2-

p

R2,

to},

i =

0,

1,

be two boxes satisfying (1.2). The box

[(xo,

to)

+

QR(I-')]

intersects

Xl

if

Ixo

-

XII

< R. Moreover they are contained in

flT

if

(4.4)

We

proceed as in the case

p>

2 and establish

258

IX.

Parabolic p-systems:

Holder

continuity of Du

LEMMA 4.2. Let (4.4)

hold.

Thereexistconstants'Y> I

andaE

(0,

I)

that

can

be

determined a priori only

in

terms

of

Nand

p,

such

thatfor all

(Xi,

to)

E

X:,

i = 0,

I,

4-(iii). A

version

of

Theorem

1.1

Combining Lemmas

4.1

and 4.2 gives the following fonn

of

Theorem

1.1

THEOREM

1.1"

(THE

SINGULAR CASE I < p < 2) .. Let u be a

weak

solution

in

fh

of

the

degenerate

system

(1.1)

of

Chap.

Vl/I, and

assume

that

,.,.

=

IIDulloo,DT

<

00.

There

exist constants

'Y

> I and a E

(0,

I) that

can

be

determined a priori only

in

terms

of

N and p

such

that,

for every compact subset

X,",

ofnT.

(1.1") IDu(Xo,t

o

} -

DU(XlItl}1

(

max{lj,.,.Y}lX

o

-

xII

+

vito

-

tll)Q

~

'Y""

dist

(X,",j

r)

,

for every pair

of

points

(Xi,

ti)

Ex'"',

i=O,

1.

Remark

4.1. The constants

'Y

and a

are

independent

of

dist.

(X,",j

r)

and,.,..

Arguing

as

in

§3-(III),

the

HOlder

continuity of Ui,:J:j can be expressed in

tenns

of

the intrinsic parabolic distance ,.,.-dist

(X,",j

r).

5.

Some algebraic

lemmas

We

let

QR(,.,.)

c

nT

be

a cylinder satisfying (1.2) and consider the system

(5.1) !

Ui

- div

IDul

p

-

2

DUi

=

0,

in

QR(""),

p >

I,

and the one obtained by taking the derivative with respect to

Xj'

i.e.,

(5.2) ! Ui,:J:; - div

(IDU

IP

-

2

DUi,:J:;

+

a:;

IDuI

P

-

2

DUi) =

0,

in

QR(""),

i=I,2,

...

,m,

i=I,2,

...

,N.

We

let V denote a vector in R

Nxm

satisfying

(5.3)

We

also let 'Y='Y(N, p) denote a generic positive constant that can be detennined

a priori only

in

tenns

of

the indicated quantities.

5.

Some

algebraic lemmas 259

LEMMA 5.1.

There

exists

a constant

'Y

= 'Y(N,p).

such

that

lor

every

vector

V E RNxm. and

lor

all p >

1.

(5.4) {lDul +

IVI)Y

IDu - VI:5 'YIIDuIY

Du

-IVIYVI·

LEMMA 5.2. Let 1 < p <

2.

There

exists a constant'Y = 'Y(N,p)

such

that lor

every

vector

V E R

Nxm.

(5.S)

IIDuIP-2

Du

- IVlp-

2

VI:5

'YIDu

- ViP-I.

Moreover

if

the

vector

V satisfies (5.3).

then

(5.6)

IIDuIP-2

Du

-IVlp-

2

VI:5

'Y,",p-

2

IDu - VI,

(S.7)

IIDuIP-2

Du

_IVIP-2vI2IDuI2-p

:5

'Y,",p-

2

IDu -

V12.

Remark

5.1.

These

lemmas

are

algebraic

in

nature

and

could

be

stated

for

any

pair of

vectors

U

and

V,

provided

(S.3)

is

replaced

by

(S.3)'

Also

in (S.4)

the

number

(1'-2)/2

could

be

replaced

by

any

number

and

in

(5.5)-

(S.7)

the

number

(1'-2)

could

be

replaced

by

any

negative

number.

PROOF

OF LEMMA 5.1:

By

calculation.

IIDulY

Du

-lvIYVIIDu

-

VI

2:

1(IDuI'i'Du-IVI'i'V,

DU-V)

I

/

f1d

Y )

=

\10

ds ISDu +

(1

- s)VI (sDu +

(1

-

slY)

ds,

Du

- V

f~

Y

=

10

IsDu +

(1

- s)VI IDu -

VI

2

ds

21~

y 2

+

p;

0 I

sDu

+

(1-

s)VI I {sDu +

(1-

s)V,

Du

- V)I

ds

f~

~

min{l;

(p

- l)}IDu -

VI

2

10

IsDu +

(1

- s)VI ds.

Ifl<p<2.

1

~

Y

o I

sDu

+

(1

- s)VI

ds

~

(IDul +

IVI)

Y ,

and

the

lemma

follows

in

this

case.

If

p > 2,

assume

for

example

that

IDul

>

IVI.

Then

260

IX.

Parabolic

p-systems:

Hi)lder

continuity

of

Du

1

~

11

IsDu +

{I

-

s)V/

ds

~

{sIDul-

(I -

s)IVI)

~

ds

o

1/2

1 1!=.!

~

-

IDul--'--

.

p

PROOF

OF

LEMMA

5.2: For

1<p<2.

write

/IDul,,-2

Du

-

IVI,,-2V/

~

IVI,,-2IDu

-

VI

+

/IDul,,-2

-IVI,,-2/I

Du

l

~

IVI,,-2IDu

-

VI

(

IDu~-1

)

+

{2

-

p)IVI,,-2IDu

-

VI

eIVI,,-1

+ {I _

e)IDul,,-l

'

for some e E [0,1]. Interchanging the role

of

Du

and

V gives

(5.8)

/IDul,,-2

Du

-

IVI,,-2vl

~

IVI,,-2IDu

-

VI

{ 1 + (2 - p)

eIVI,,-1

~~71~-;)IDUI"-1

} •

for

some e E

[0,

1].

and

(5.8')

IIDul,,-2

Du

-

IVI,,-2vl

{

IVI,,-I}

~

IDul,,-2IDu

-

VI

1 +

(2

-

p)

'1I

V

I,,-1

+

(1

_ '1)IDul,,-1 '

for some 'IE [0,1].

To

prove (5.5) assume rust that

(5.9)

1

IVI>

"2

IDu

-

VI·

This implies

These inequalities

in (5.8) prove (5.5). If (5.9) is false.

its

converse gives

the

two

inequalities

These

in

(5.8)'

imply

that the

term

in braces

on

the

right hand

side

is bounded

above

by

an

absolute constant. Moreover

IVI,,-2IDu

-

VI

~

IDul,,-2IDu

-

VI,,-IIDu

-

VI

2

-".

The

two inequalities (5.6) and (5.7)

are

an

immediate consequence of (5.8) and

the

assumption (5.3).

5.

Some

algebraic

lemmas

261

Let

H be

the

vector

in

R

Nxm

defmed

by

(5.12)

Hi

==

IDul

p

-

2

DUi

-IVlp-

2

Vi

-IVl

p

-

2

(DtI.i

-

Vi)

- (p - 2)IVlp-

4

Vt,k

(Ul,z. -

Vt,k)

Vi,

i=

1,

2,

...

,

m.

We

will

estimate

IHI

for

all

p>

1.

For

this

we

first

set

(5.13)

W(t)

==

tDu

+

(1

- t)V,

for

t E

[0,1],

and

rewrite

(5.12)

in

the

form

1

Hi

= j

~

{ltDu +

(1

- t)VIP-2 (tDui +

(1

- t)Vi)}

dt

o

-IVl

p

-

2

(DUi

-

Vi)

- (p - 2)IVlp-

4

Vt,k

(Ul,z. -

Vt,k)

Vi

1

=

(DUi

-

Vi)

j{IWIP-2

-IVI

P

-

2

}

dt

o

1

+ (p -

2)

(DUl

-

Vt)

!{IWIP-4WlWi

-IVI

P

-

4

VtVi

}dt

o

where

we

have

dropped

the

t-dependence

from

W.

From

(5.13)

(5.14)

W - V = t (Du -

V)

,

and

for

every

sE

[0,1].

(5.15)

sW

+

(1-

s)V

= V +

st(Du

-

V).

LEMMA

5.3. There exists a constant

"'(

=

"'(N,p)

such

that/or

every constant

vector V ERNxm satisfying

(5.3),

and/or

all p>

1,

(5.16)

Remark

S.2.

The

lemma

holds

for

every

pair of

vectors

U

and

V

satisfying

(5.3)'.

PROOF

OF

LEMMA

5.3 (p>2):

Assume

first

thatlVI

~

21Du

-

VI.

Then

1

IHI

~

",(p)IDu -

VI

j(IW(t)I

P

-

2

+ IVIP-2)

dt

o

~

"'(IDu

- VIP-l

~

I~I

(lDul + IVj)p-2IDu -

V12.

Therefore

(5.16)

follows

in

this

case

since

V satisfies (5.3). If

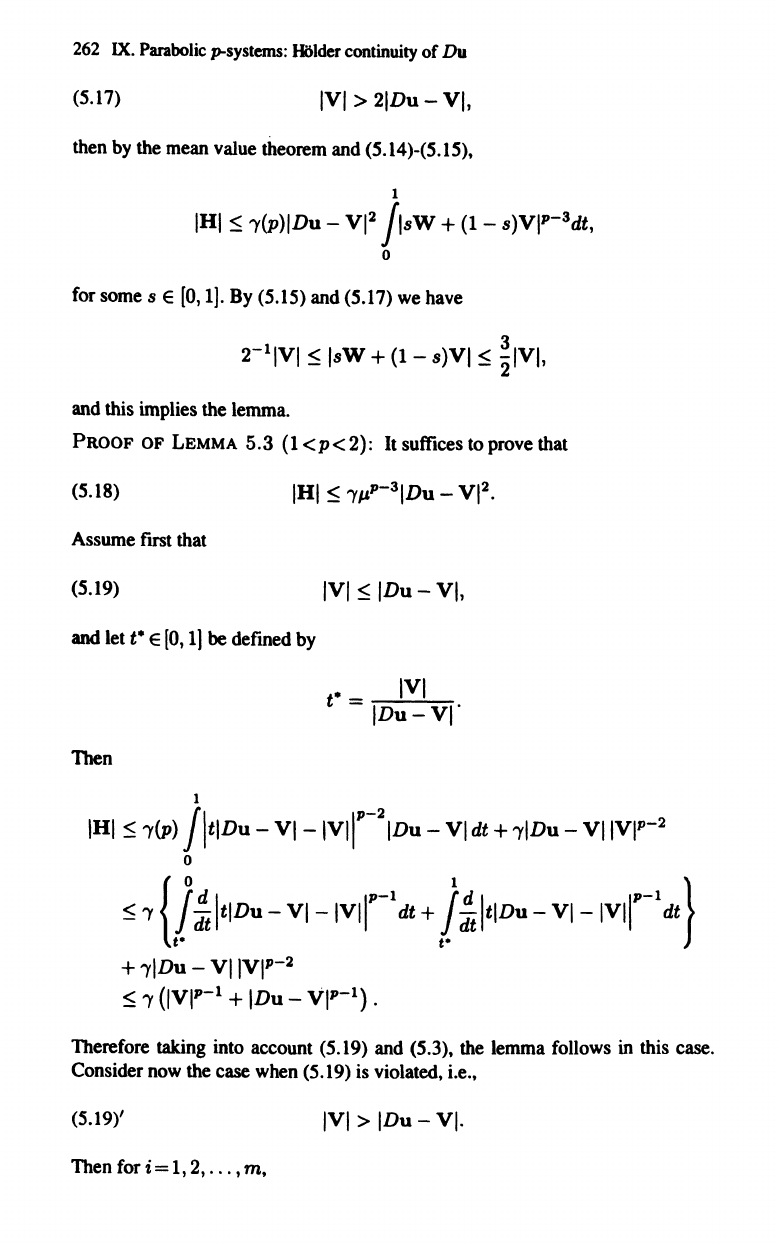
262

IX.

Parabolic

p-systems:

mlder

continuity

of

Do

(5.17)

IVI

>

21Du

-

VI,

then

by

the

mean value theorem and (5.14)-(5.15),

1

IHI

~

'Y(P)IDu

-

VI

2

flsW

+

(1

-

s)VIP-

3

dt,

o

for some s E [0,1]. By (5.15) and (5.17)

we

have

and this implies the lemma.

PROOF

OF

LEMMA

5.3

(1<p<2):

Itsufticestoprovethat

(5.18)

Assume first that

(5.19)

and

let

t·

E

[0,

1]

be

defined by

Then

1

IVI

~

IDu

-

VI,

t.

=

IVI

IDu-VI

IHI

~

'Y(P)

fltlDu

-VI_IVIIP-2IDu -

VI

dt +

'YIDu

- VIIVl

p

-

2

o

,;;

~

{l

~

l'IDu

-

VI

-IVlr'

<It

+

i!

l'IDu

-

VI-IVf'

tit }

+

'YIDu

- VIIVI

P

-

2

~

'Y

(lVIP-l +

IDu

- VIP-l) .

Therefore taking into account (5.19) and (5.3), the lemma follows

in

this case.

Consider

now

the

case when (5.19)

is

violated, i.e.,

(5.19)'

IVI

>

IDu

-

VI·

Then for i =

I,

2,

...

,m,

6. Linear parabolic systems with constant coefficients 263

1 1

Hi =

(DUi

-

Vi)

I I

:al

sW

+

(1-

s)VIP-

2

dsdt

o 0

1 1

+

(DUl

- Vi) I

l:a

{lsW

+

(1-

S)VIP-4

(SWl +

(1-

s)Vl)

o

0

X

(sW

i

+

(1

- s)Vi)

}ds

dt.

Therefore

1 1

(5.20) IHI

~

'Y(p)IDu

- VI

2

I

It

IsW +

(1-

s)VIP-

3

dsdt.

o 0

Next, by (5.15) and (5.19)'

IsW +

(1

- s)VI =

Iv

+

st(Du

- V)I

~

IIVI-

stlDu

- VII

~

IVI(1 - st).

This in (5.20) gives

1 1

IHI

~

'YIDu

-

V1

2

1

V

l

p

-

3

Ilt(1

- st)P-

3

ds

dt.

o

0

Since 1 <p <

2.

the last integral is finite and the Lemma follows.

6. Linear parabolic systems with constant coefficients

Let V

be

any vector in RNxm satisfying (5.3). To the system (5.1) we associate

its linearised version

(6.1)

a

at

Vi

- (IVIP-2

Vi

,Xt

+ (p -

2)IVIP-4Yj,kVj,x~

Vi,l)

Xt

'

in

QR(J.£),

i =

1,2,

...

, m.

Let

v

==

(Vl,V2,

...

,v

m

)

and for 0 < p

~

R we let (Dv) p denote the integral average

of

Dv

over Q p

(1-£).

264

IX.

Parabolic p-systems:

mlder

continuity

of

Do

THEOREM

6.1.

There

exists

a constant'Y='Y(N,p).

such

thatforall O<p:SR.

and for

every

constant

vector

WE

R

Nxm.

(6.2) H

IDv

-

(Dv)p

1

2

dxdT

:S

'Y

(~)

2 H

IDv

-

W1

2

dxdT.

~w

To

prove

the

theorem

we

introduce

the

change of variables

v(x, t) - V

(x,

tp.2-,,) .

This transfonns Qp(p.) into Qp(l)

==

Qp

for all 0 < p:S R. and tranfonns (6.1)

into a system

for

which

In

a precise

way,

the

transfonned vector v

is

a solution of

(6.3)

8 ( . . )

at

Vi

-

a~:~

Vi,z.

Zt

= 0,

where the coefficients

a

i,j

=

IVI,,-2

{flij

+ (p _

2)

\-j,ll:

Vi,t

}

t,ll: - t,lI:

IVI2

satisfy

the

ellipticity condition

(6.4) C

o

(N,p)leI

2

:S

a~~lI:eiltej,ll:

:S

C

1

(N,p)lel

2

,

Ve

E

RNxm,

for

two given constants

Co

< C

1

depending only

upon

N and p. Therefore it

will

suffice

to prove

Theorem

6.1

for

p.

=

1.

In

the remainder of the section

we

let v be

a solution of (6.3)

in

QR and let (6.4) hold.

Let

a denote a multiindex of size lal.

i.e.,

N

a==(al,a2,

...

,aN),

ajENU{0},j=l,2,

...

,Nj

lal=Laj,

j=1

and for f E

Coo

(Q

R)

let

For non-negative integers m

and

n

we

also set

ID;'fl

==

L ID:II,

lal=m

D~f==

~f,

ID:fl =

ID~II

= III·

LEMMA

6.1.

There

exists

a

constant

'Y

= 'Y(N,p)

such

that for all

non-negative

integers

m, n and all 0 <

p:S

R,

6.

Linear

parabolic

systems

with

constant

coefficients

265

(6.5)

ffID,:+lD~VI2

dxdT

~

'YP-2

ffID':D~VI2

dxdT,

Qp/2

Qp

(6.6)

f!IDf+lD':VI

2

dxdT

~

'Yp-

4

!!ID':D~VI2dxdT.

Qp/2

Qp

PROOF:

The system (6.3)

is

also solved

by

the

vectors W

==

D';Div.

Let

(be

a non-negative smooth cutoff function

in

Q p vanishing on the parabolic boundary

of

Q p and such that

Multiply

the

system (6.3), written for w,

by

the testing function

W(2

and

integrate

over

Qp.

to

arrive

at

(6.5).

To

prove (6.6).

mUltiply

the

same

system

by

Wt(2

and

integrate over Qp. This gives

(6.7)

!!lwtI2(2dXdT+

!!

(a~,,{Wj,z,,!

Wi,Zt)

(2dxdT

Qp Qp

=

-2

f!a~:{Wj'Z"Wi,t«ZtdxdT

Qp

+~

!

!IWtl2(2dXdT

+

;!

!IDwI

2

dxdT.

Qp

The integral involving

a~:{

on the left

hand

side of (6.7) equals

These remarks

in

(6.7)

give

!!IWtI2dxdT

~

'Yp-

2

!!IDw

I2

dXdT.

Qp/2

Qp

The

lemma

now

follows

by

applying (6.5) and suitably modifying the scale of

the

radii P

and

p/2.

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.