DiBenedetto E. Degenerate Parabolic Equations

276

IX.

Parabolic

p-systems:

Jl)lder

continuity

of

Du

I

PDU

- V

l

2

dxdT

:5

"Yeo

IIIDU

- V

o

l

2

dxdT

Qu(,,)

QIl(")

+ I

fiDV

- Vl l

2

dxdT.

Qu(,,)

By

Theorem

6.1

lfiDV

- Vl l

2

dxdT:5

"Y6

N

+4IIIDv

- V ol

2

dxdT,

Q,Il(")

QIl/2(")

and

again

by

Lemma

7.2

with

V = V 0 and (8.2)

II

IDv

- V

o

l

2

dxdT

:5

"Y

(1

+

EO)

I

IIDU

- V ol

2

dxdT,

QR/2(")

QR(")

for a constant

"Y="Y(N,p).

Combining these inequalities

we

obtain

I

fiDU

- Vll2dxdT:5

"Y

(6

NH

+eO)

IIIDU

- V

o

l

2

dxdT,

6:5 1/2.

Q,Il(")

QIl(")

To

prove (8.4) choose

EO

=6

NH

, and then 6 so small that

2"Y6

2

:5

".

Inequality

(8.5)

follows from (8.4) and the

s1I1Illiness

assumption (8.2).

To

prove

(8.3) write

and

V

l

-

Vo

= H

(Dv

- Vo)dxdT

Q,R(")

= H

{(Dv

- Du) +

(Du

-

Vo)}dxdT

Q,R(")

IV

l

-

V

o

l

2

:5

2 H

IDu

- Dvl2dxdT + 2 H

IDu

- V

o

l

2

dxdT.

QIIl(")

Q,R(")

By

Lemma

7.2

and

the

indicated choices of E

and

6

H IDu - Dvl2dxdT

:5

" H IDu - V ol

2

dxdT.

~RW

Therefore using again (8.2)

8.

Proof

of

Proposition 1.l-(i)

277

(8.6)

IV

1 - V

o

l

2

~

2

(K,

+ 6-(N+2») H

IDu

- V

o

l

2

dxdT

Qa(,,)

~

2 (

K,

+

6-(N

+2)

) dl

2

(NH)

p.2

~

2K,p.2.

By

choosing

K,

sufficiently small we may insure that

and

LEMMA

8.2.

There

exist constants

K"

6,

EE (0,1) that

can

be determined a priori

only

in

terms

of

N and p.

such

that

if

V 0

is

a constant

vector

in

R

Nxm

satisfying

(8.1)

and (8.2).

then

there

exists a

sequence

of

constant

vectors

{Vi}

el

in

RNxm.

satisfying

(8.8) H

IDu

- Vil2dxdT

~

E

p.2,

Q6

I

a(")

(8.9)

!

!IDU

- Vi+!1

2

dxdT

~

K,6

N

+

2

!/IDU

- V

i

l

2

dxdT,

Q6l+

1

a(")

Q6

I

a(")

for i = 1, 2,

..

"

PROOF:

The sequence is constructed inductively

by

using the procedure

of

the

previous lemma. To prove that

IVil

are in the range (8.7), we refer back to (8.6),

i.e.

IV

i

+!

- V

i

l

2

~

2

(K,

+ 6-(N+2») H

IDu

- V

i

l

2

dxdT.

Q6

I

a(")

We iterate over i and use again the

smallness

assumption (8.2) to obtain

IVi+l

- V

i

l

2

~

2

(K,

+ 6-(N+2»)

K,i

H

IDu

- V

o

l

2

dxdT

Qa(,,)

~

2p.

2

6

2

(NH)

(K,

+ 6-(N+2»)

K,i.

From this by taking roots and adding over i

00.

,fK.

I

V

i+l

- Vol

~

P.6L.,fit

~

p.

1-

,fK.'

i=l

278

IX.

Parabolic

p-systems:

Ifi)lder

continuity of Du

where

we

have

used

the

specific choice of 6

in

tenns of

It.

Choosing

now

It

suffi-

ciently

small

proves

the

Lemma.

9. Proof of Proposition 1.1-(ii)

The

number

11

in

the

assumption

(1.3)

can

be

chosen

to

insure

the

existence of a

constant vector

Vo E

RNxm

satisfying

(8.1)

and

(8.2).

This

is

the

content of

this

section. Set

IDul

= v

and,

for

all

0 < p

~

R,

(9.1)

A;

==

((x,t)

E

Qp(l-')

Iv(x,t)

> (1-1I)1-'},

(9.2)

B;

==

{(x, t) E

Qp(l-')

Iv(x,

t) <

(1

- II)I-'} .

We

will

choose

11

E (0,

l)

and

rewrite

(1.3)

as

(9.3) IBill

~

IIIQR(I-')I,

11

E (0,1)·

LEMMA

9.1.

There

exists

a constant.'Y='Y(N,p)

such

that/or all

uE

(0,1)

(9.4)

jr

fIDul,,-2ID2uI2

dxdT

<

'Y

1-'211

RN.

P -

(1-

u)2

A:

1t

PROOF:

Consider

the

differentiated equation (S.2)

and

in

its

weak

fonnulation

take

the

testing

function

Ui,z;

(v

2

- k

2

)+

(2,

k =

(1-

211)1-',

modulo

a

Stelclov

averaging

process.

Here

(

is

a non-negative piecewise

smooth

cutoff

function

in

Q R

(I-')

that

equals one

on

Q

tT

R

(I-')

and

such

that

1

1-',,-2

ID(I

~

(1-

u)R'

0 $

(e

$

(1-

u)W'

After

we

add over i =

1,

2,

...

I m

and

j =

1,

2,

...

, N,

we

arrive at

(9.S)

SUP.

/(,:,2

- k2):

(2

(x,

t)

dx

-",3-PR2<e<o

- -

Kit

+ / /vP-2IDv212(2x.

[v>

k]

dxdT

QIt(,,)

m N

+

?:?:

/ /IDu

l

,,-2I

DUi

,z.:/

12

(v

2

-

k

2

)+

(2dxdT

1=1

.1=1

Q"It(")

$

'Y

/ /vP-2IDv21

(v

2

-

k

2

)+

(ID(I

dxdT

QIt(",)

+

'Y

//(v

2

- k2):

((t

dxdT

QltC,,)

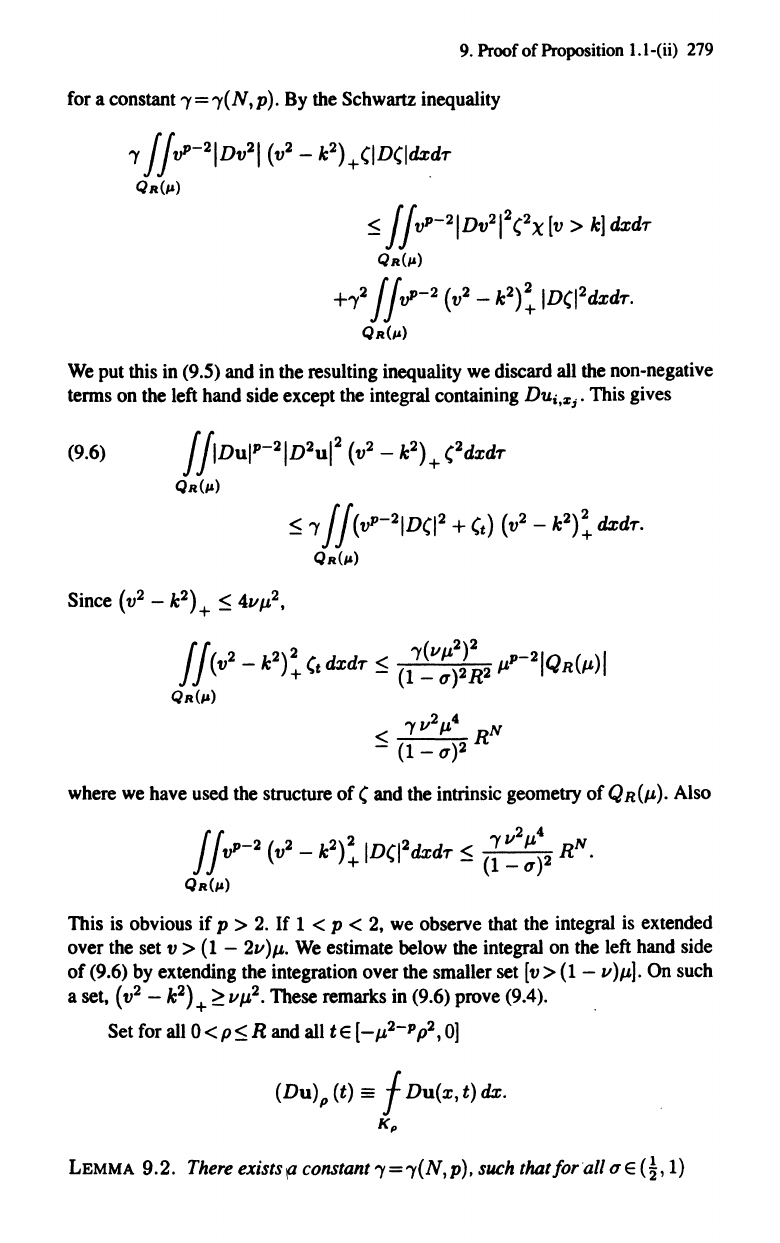
9. Proof of Proposition

l.l-(ii)

279

for a constant

"Y="Y(N,p).

By

the Schwartz inequality

"Y

jjvP-

2

I Dv

2

I

(v

2

- k

2

)+(ID(ldx.dT

QR(p)

~

jjvP-2IDV212(2X[V > k]dxdT

QR(p)

+"Y2

j j

vP-

2

(v

2

- k2):

ID(1

2

dxdT.

QR(P)

We

put this

in

(9.S) and

in

the resulting inequality

we

discard all the non-negative

terms

on

the left hand side except the integral containing

DUi,Zi'

This gives

(9.6)

fjlDulP-2lD2ul2

(v

2

- k

2

)+

(2clxdT

QR(P)

~

"Y

j

j(vP-2ID(12

+

(t)

(v

2

- k2):

dxdT.

QR(p)

Since

(v

2

- k

2

)

+

~

411J.1.2,

jj(v

2

- k2):

(t

clxdT

~

(1"Y~:;~~2

J.l.

P

-

2

IQR(J.I.)1

QR(P)

where

we

have used

the

structure of

(and

the

intrinsic geometry of

QR(J.I.).

Also

f

r

fvP-2

(v

2

_ k

2

)2

ID(1

2

dxdT

<

"Y

1I2

J.1.4.

RN.

j'

+ - (1-0')2

QR(P)

This

is

obvious

if

p >

2.

If

1 < p <

2,

we

observe that the integral

is

extended

over the set

v > (I -

211)J.I..

We

estimate below the integral on the left

hand

side

of

(9.6)

by

extending the integration over the smaller set [v> (I -

II

)J.I.].

On

such

a set,

(v

2

- k

2

)

+

~

IIJ.1.2.

These remarks

in

(9.6) prove (9.4).

Set

for

all

O<p~R

and

all

tE

[-J.l.

2

-

p

p2,O]

(Du)p

(t)

==

f

Du(x,

t)

dx.

Kp

LEMMA 9.2.

There

ex;sts'(l

constant

"Y="Y(N,p).

such

that/or

'all

O'E

(l,l)

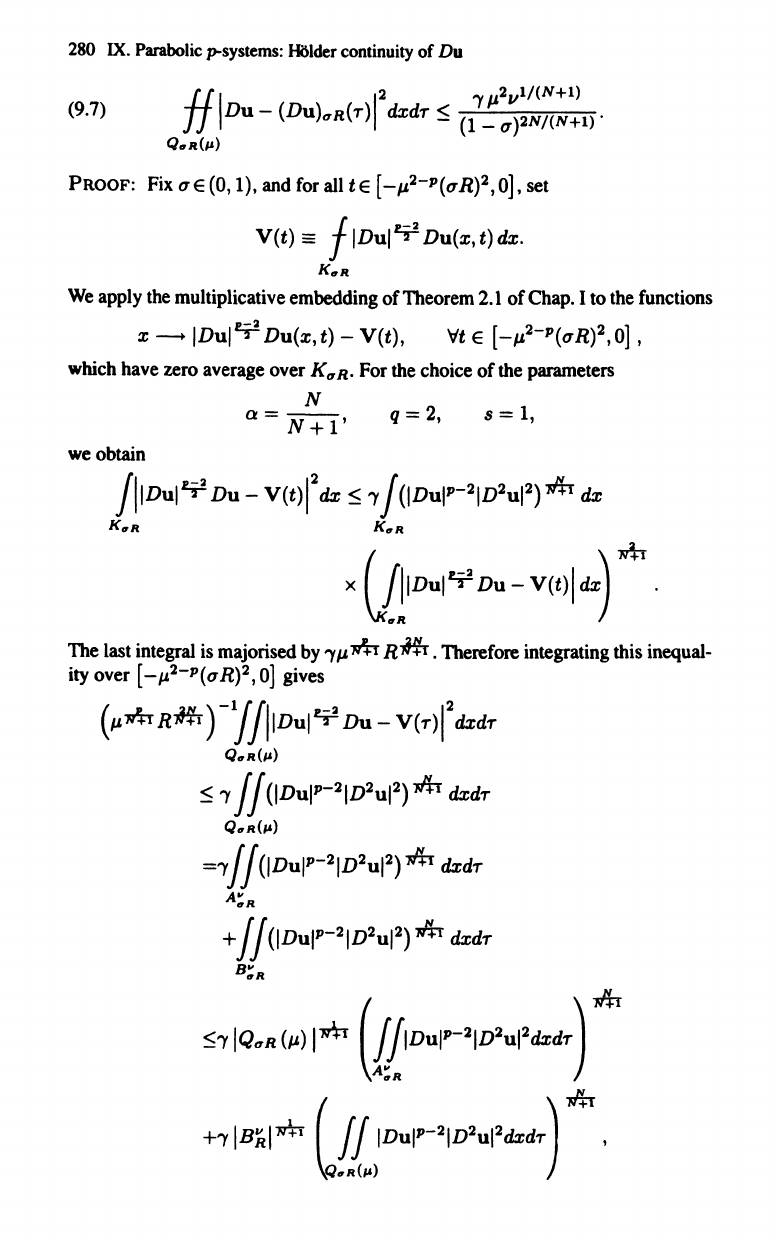
280

IX.

Parabolic

p-systems:

H5lder

continuity of

Du

PROOF:

Fix

UE(O,

1).

and

foraH

tE

[-1£2-

P

(uR)2,O]. set

Vet)

==

f

IDulEj!

Du(x, t)

dx.

K"R

We

apply

the

multiplicative embedding of

Theorem

2.1

of

Chap.

I

to

the

functions

x

-+

IDulEj!

Du(x,t)

- Vet),

'Vt

E [-1£2-p(uR)2,O],

which

have

zero

average

over

KtrR.

For

the

choice of

the

parameters

N

Q = N + 1 ' q =

2,

s =

1,

we

obtain

IIIDulEj!

Du

- V(t)1

2

dx::5

"Y

IODUIP-2ID2uI2)

JIh

dx

~R

x

V!IDuI'i'Du-V<tlldz)

~

The

last integral

is

majorised

by

''/#£

rn

R-Af:r

. Therefore integrating this inequal-

ityover

[-1l

2

-

P

(uR)2,O]

gives

(Il

rn

RHr)

-j

IIIDu1lj!

Du

-

V(r)r

dxdr

Q"R(/J)

::5

"Y

II

ODuIP-2ID2uI2)

Jfh

dxdr

Q..RC/.')

="YI

!(IDUIP-2ID2uI2)

JIh

dxdr

A:

R

+ IloDUIP-2ID2uI2)

JIh

dxdr

B:

R

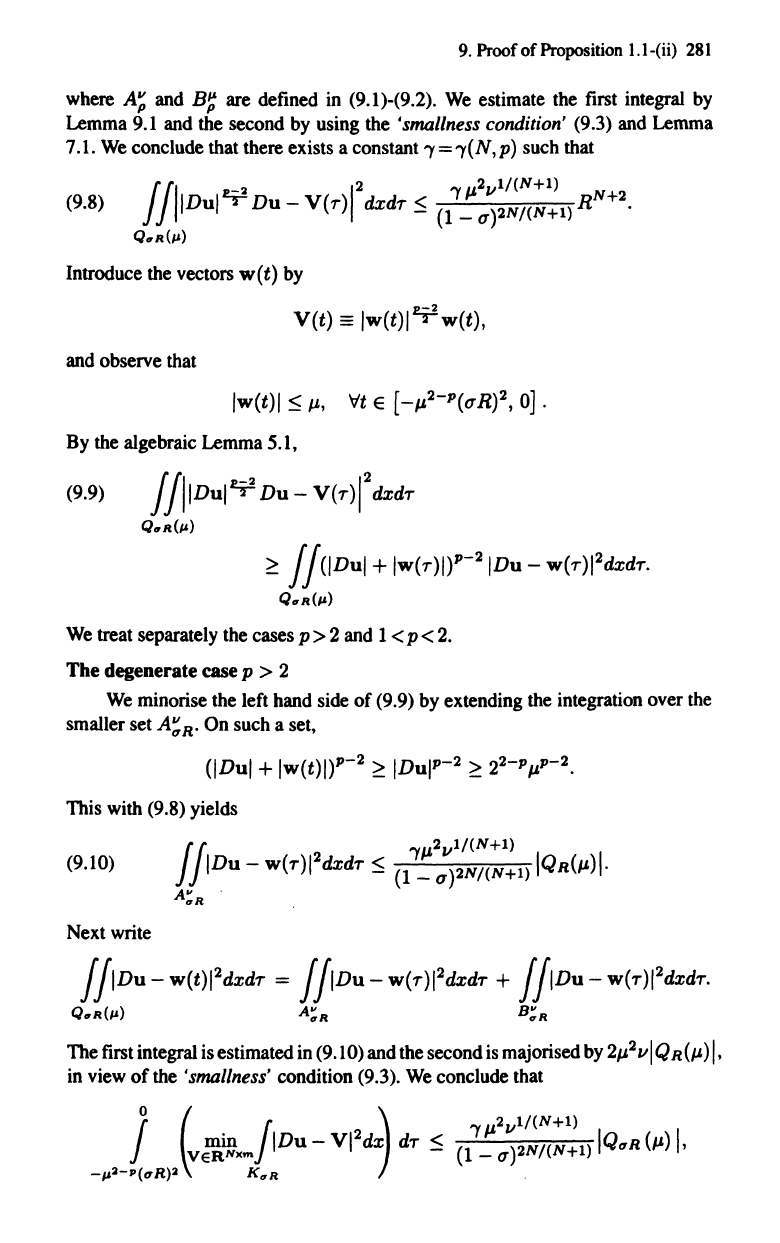
9.

Proof of

Proposition

l.l-(ii)

281

where

A~

and

B:

are defined in (9.1)-(9.2).

We

estimate the first integral by

Lemma 9.1 and the second by using the

'smallness condition' (9.3) and Lemma

7.1.

We

conclude that there exists a constant 'Y='Y(N,p) such that

f

r [I ¥

12

'Y

1J2

V

l/(N+l)

N+2

(9.8) 1

IDul

Du

-

VCr)

dxdr

~

(1

_

u)2N/(N+l)

R .

Q..R(p)

Introduce the vectors wet) by

Vet)

==

Iw(t)l¥w(t),

and observe that

Iw(t)1

~

IJ,

'<It

E

(-1J

2

-

P

(uR?,

0]

.

By

the algebraic Lemma 5.1.

(9.9)

IIIIDu

l

¥

Du

- v(r)1

2

dxd7'

Q"It(p)

~

II(lDu

l

+ Iw(r)I),,-2IDu -

w(7')1

2

dxd7'.

Q"It(p)

We treat separately the cases

p>

2 and 1 < p <

2.

The degenerate case p > 2

We minorise the left hand side

of

(9.9)

by

extending the integration over the

smaller set

A~R'

On

such a set.

(lDul + Iw(t)l)P-2

~

IDul,,-2

~

2

-"IJ

P

-

2

•

This with (9.8) yields

[ [ 2

'Y1J

2

v

1

/(N+l)

(9.10)

11

IDu -

W(7')1

dxd7'

~

(1-

u)2N/(N+l)

IQR(IJ)I·

A~1t

Next write

IIIDU

-

w(t)1

2

dxdr =

IIIDU

-

w(7')1

2

dxd7'

+

IIIDU

-

w(7')1

2

dxd7'.

Q"It(p)

A~1t

B~1t

The first integral is estimated in (9.10) and the second is majorised by

21J2

vi

Q R

(IJ)

I.

in view

of

the 'smallness' condition (9.3). We conclude that

282

IX.

Parabolic p-systems:

HOlder

continuity of

Du

for a constant

"(

=

"(N,p).

The minimum on the left hand side is achieved for

V

==

(Du)aR (t). This proves the lemma

if

p>

2.

The

singular

case 1 < p < 2

Since

!w(t)!

:5

,.,.,

we have (/Du! + !w(t)l)P-2

~

2

P

-

2

,.,.p-2.

Putting this in

(9.9) and combining it with (9.8) gives

j

r r 2 "(

,.,.2

v

l/(N+l)

J

!Du

- w(t)! dxdr:5

(1

_ u)2N/(N+l)

IQaR

(,.,.)

I·

Q"R(/J)

The proof is now concluded by a minimization procedure.

10. Proof

of

Proposition 1.1-(iii)

Let (Du)p denote the integral average

of

Du

over

Qp(""),

i.e.,

(Du)p

==

H

Dudxdr.

Qp(/J)

LEMMA

10.1. There exists positive constants

"(,

a, b that can be determined a

priori only in terms

of

N

and

P.

such that

for

all u E

(i,

1).

(10.1) H IDu - (Du)aR 1

2dxdr

:5

"(,.,.2

{(I

~au)b

+

(1-

u)}

.

Q"R(/J)

PROOF: By Lemma 9.2

and

H

2 "(

,.,.2

v

l/(N+l)

IDu

- (Du)aR I dxdr

:5

(1-

u)2N/(N+l)

Q"R(/J)

+

HI

(DU)aR

-

(DU)aR

(r)1

2

dxdr

Q"R(/J)

(10.2)

HI

(DU)aR

-

(DU)aR

(r)1

2

dxdr

Q"R(/J)

:5

sup I f

(Du(x,t)

- DU(X,8»)

dx12.

-"l-P(aR)l<t

s<O

r-

- , -

KtlR

Let u =

(1

+ u)

/2

and denote with x

--+

('

(x) a non-negative smooth cutoff function

in K a R that equals one on K a R and such that

10.

Proof of Proposition l.1-(iii)

283

- 2 4 I

2-1

16

ID{I

~

(1-

u)R

==

(1-

u)R'

D {

~

(1-

u)R'

Write

j (Du(x, t) - Du(x,s») dx = j

(Du(x,t)

- Du(X,7'»)(2dx

K"R

a-KR

-

j(Du(x,t)

- Du(x,s»)(2dx.

K.R\K"R

The last integral is estimated above

by

'Y(l - u) IJRN.

To

estimate the

fIrSt

integral

we

integrate

the

differentiated system (5.2) over

(7',

t). multiply

by

(and integrate

over

Ka-R.

This gives

(10.3) j (Ui'lI:i (t) -

Ui,lI:i

(s)

)(2

dx

K.R

=

Ii

f

('

div (

.,..-'

Du;

..

, +

0:;'

Do;)

""dBl·

aK.R

Thecasep>2

The right

hand

side of (10.3)

is

estimated

by

To

estimate

the

last integral write

jjlDull.jllD2Uldxd7'

= jjlDU

1

1.jllD

2

u

1

dxd7'

~RW

~R

+ j

jIDul2.j2ID2Uldxd7'

B;R

~

IQR(IJ)I!

(f!IDuIP-'ID'U1'''''tt.!

!

Au

)

+ IBill! (!!I

Du

Ip-2ID'U

1

'''''tt.!!

Qu(,,)

)

284

IX.

Parabolic

p-systems:

mlder

continuity

of Du

The

frrst

integral

is

estimated

by

Lemma

9.1

and

the

second tenn is estimated

by

the 'smallness' condition (9.3) and

Lemma

7.1. Combining these estimates

in

(10.2) proves

the

lemma.

The case

l<p<2

Estimate

the

right

hand

side of (10.3)

as

follows.

I

I(

Ui,:J:;

(t) -

Ui,:J:;

(8)

)(2

dx

~u

= V /

D(-'

{IDol"""

Du

-

I(Du)'R

(s)l.-2

(Du)'R

(sn.,

dzdTl

sK.R

t

~

I IID

2

(IIiDuI

P

-

2

Du

-I

(DU)uR

(8)11'-2

(DU)uR

(8)1

dxdr.

sK;;R

By

the

sttucture of

the

cutoff function (

and

(5.5) of

Lemma

5.2, this

is

majorised

by

t

(1

_

!)2

R2

IllDu

- (Du)uR (s)l"-1 dxds

SK.R

We

estimate the last integral

by

Lemma

9.2 and combine it

with

(10.3) to prove

the

lemma.

11.

Proof

of

Proposition

1.1

concluded

LEMMA 11.1. Let e E

(0,

1)

be

the

number

claimed

by

Lemma

B.l.

There

exists

a

number

v E

(0,

i)

such

that

if (9.3)

holds,

then

(11.1)

(11.2)

PROOF:

Write

H

IDU

-

(DU)RI

2

dxdr

~

ep.2,

QR(")

II.

Proof of Proposition

1.1

concluded

285

H IDu - (Du)RI

2

dxd".

= U

N

+

2

H IDu -

(DU)aRI

2

dxd".

Q

RC,,)

Q.RC,,)

+ IQR(P.)1-1jjIDU -

(Du)Rr

dxd".

QR(,,)\Q.RC,,)

+ u

N

+

2

H I(Du)R -

(DU)aRI

2

dxdT.

Q.R(")

The flrst integral is estimated by Lemma 10.1 and the second is bounded above by

"Y(1

- q)p.2. To estimate the last integral write

(DU)R-(Du)C7R

=

IQC7R

(p.)

1-

1

{U

N

+

2

jj

Dudxd". - j j DUdxd".}

QRC,,)

Q.RC,,)

=

IQC7R

(p.)

1-

1

{

{u

N

+

2

-

lif

j Dudxd". + j j DUdxdT} .

QR(,,) QRC,,)\Q.RC,,)

This implies that

and

H IDu -

(DU)RI

2

dxdT

:s

"Y

p.2 {

(1

:ou)b +

(1

- u) } .

QR(")

To prove (11.1) choose u so close to one that "Y(I- u)

:s

~e.

and then v so small

that

"YvO(1

-

u)-"

:s

~e.

To prove (11.2) we flrst observe that the deflnitions

(9.1)-(9.2)

imply

Then by the

'smallness' assumption (9.3)

jjlDu

I2

dxdT

~

jjlDU

I2

dXdT

~

p.2(1_

v)3IQR(P.)I.

QRC,,)

Ail

Using now (11.1)

H

IDul

2

dxd". - H

(Du)~dxd".

= H IDu - (DU)Rr

dxd".

QRC,,) QRC,,) QRC,,)

:s

ep.2.

From this

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.