DiBenedetto E. Degenerate Parabolic Equations

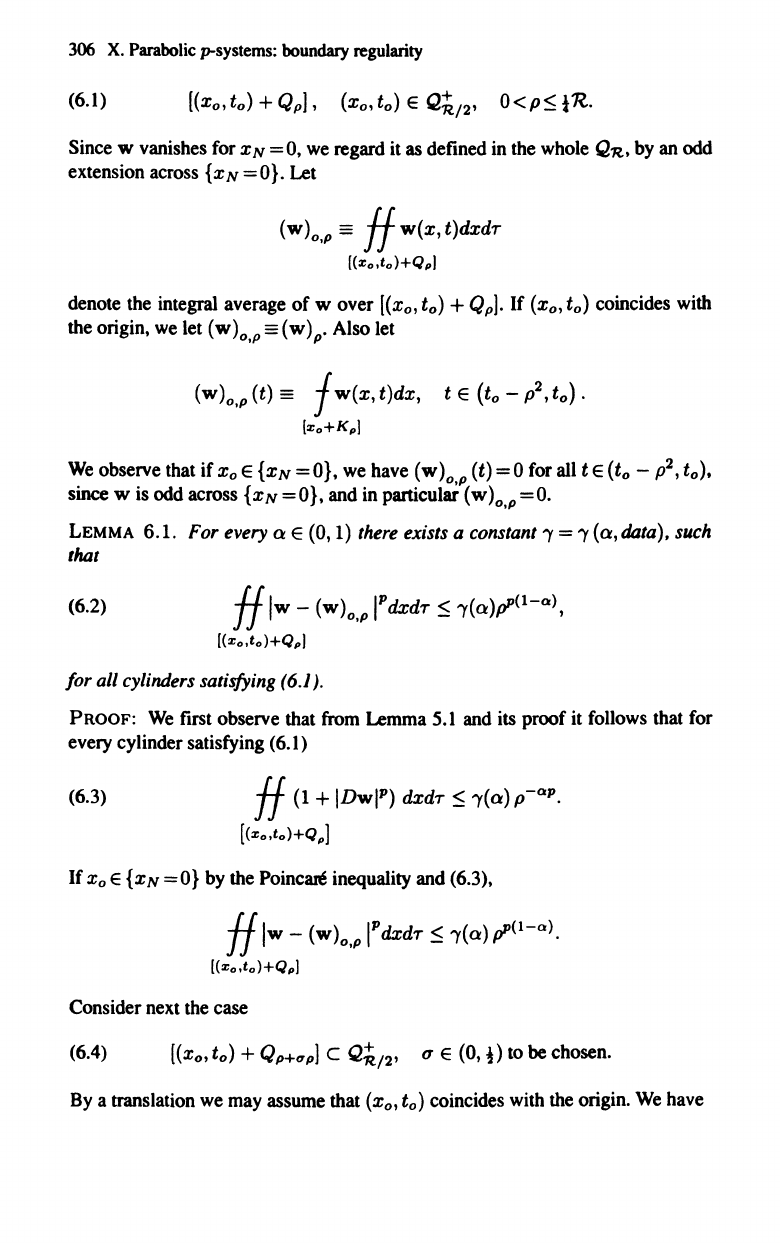
306

X.

Parabolic

p-systems:

boundary

regularity

Since

w vanishes for

XN

=0,

we regard it as defined in the whole QR, by an odd

extension across

{x N = o}. Let

(w)o,p

==

HW(X,t)dxdr

[(zo,to)+QpJ

denote the integral average

of

w

over

I(x

o

,

to)

+

Qp].

If

(x

o

, to) coincides with

the origin, we let

(w)o,p==(w)p' Also let

(w)o,p

(t)

==

f w(x, t)dx, t E

(to

-l,

to).

{zo+KpJ

We observe that

if

Xo

E

{XN

=O},

we have

(w)o,p

(t)

=0

for all t E

(to

- p2, to).

since w is odd across

{XN

=O},

and in particular

(w)o,p

=0.

LEMMA

6.1.

For

every a E (0,1)

there

exists a constant

"(

=

"(

(a, data),

such

lhat

(6.2)

H

Iw

-

(w)o,p

I

P

dxdr

:5

"((a)pp(l-OI),

[(zo,to)+QpJ

for all cylinders satisfying (6.1

).

PROOF:

We first observe that from Lemma 5.1 and its proof it follows that for

every cylinder satisfying (6.1)

(6.3)

H

(1

+ IDwIP) dxdr

:5

"((a)

p-OIP.

[(zo,to)+Qp]

If

Xo

E

{XN

=O}

by

the Poincare inequality and (6.3).

H

Iw

-

(w)o,p

I

P

dxdr

:5

"((a)

pp(l-OI).

{(zo,to)+QpJ

Consider next the case

(6.4)

[(xo,

to)

+

Qp+ap]

C

Q~/2'

U E (0,

l)

to

be

chosen.

By a translation we may assume that (xo,

to)

coincides with the origin. We have

6.

Estimating the

local

averages

of w (the case p >

2)

3C17

H

Iw

-

{w)pIP

dxdT

:5

H

Iw

-

{w)p

{T)I

P

dxdT

Qp Qp

+

HI

{W)p

(T)

- (w)p I

P

dxdr

Qp

==

](1)

+

](2).

By the Poincare inequality and (6.3)

](1)

:5

')'{a)

{I'(I-a).

](2)

= H / H

[w{x,

t) -

w{x,

r)]

dxdrr

dxdt.

Qp

We

estimate the integrand on the right hand side

of

(6.5) by making use

of

the

equation (2.5), over the cylinder Q

P+tT

p.

Let x

-+

({

x) be a non-negative piecewise

smooth cutoff function in K

p

+

tTP

that equals one on Kp and such that

ID(I

:51/

up.

In the weak formulation

of

(2.5), take ( as a testing function and integrate over

K

p

+

tTP

x

[T,

t]

to obtain

/ ! ([w{x,

t)

-

w{x,

r)]

dx/

Kp+"p

:5

t

!!IAi{X,w,

Dw).D(+At(xt+Bi(ldxdT

1=1

Qp+"p

:5

u'Yp!

/(1

+

IDwIP-1)

dxdT

Qp+"p

By

the properties

of

( and (6.3) with a suitable choice

of

a we conclude that

1/

[w{x,

t) -

w{x,

T)]

dxl

:5

~pN+(I-a)

l(p

+ /

/[w{x,t)

- w{x,T)]dxl.

Kp+"p\K

p

Let

{w)P+tTP

denote the integral average

ofw

over the

Qp+tTP,

i.e.,

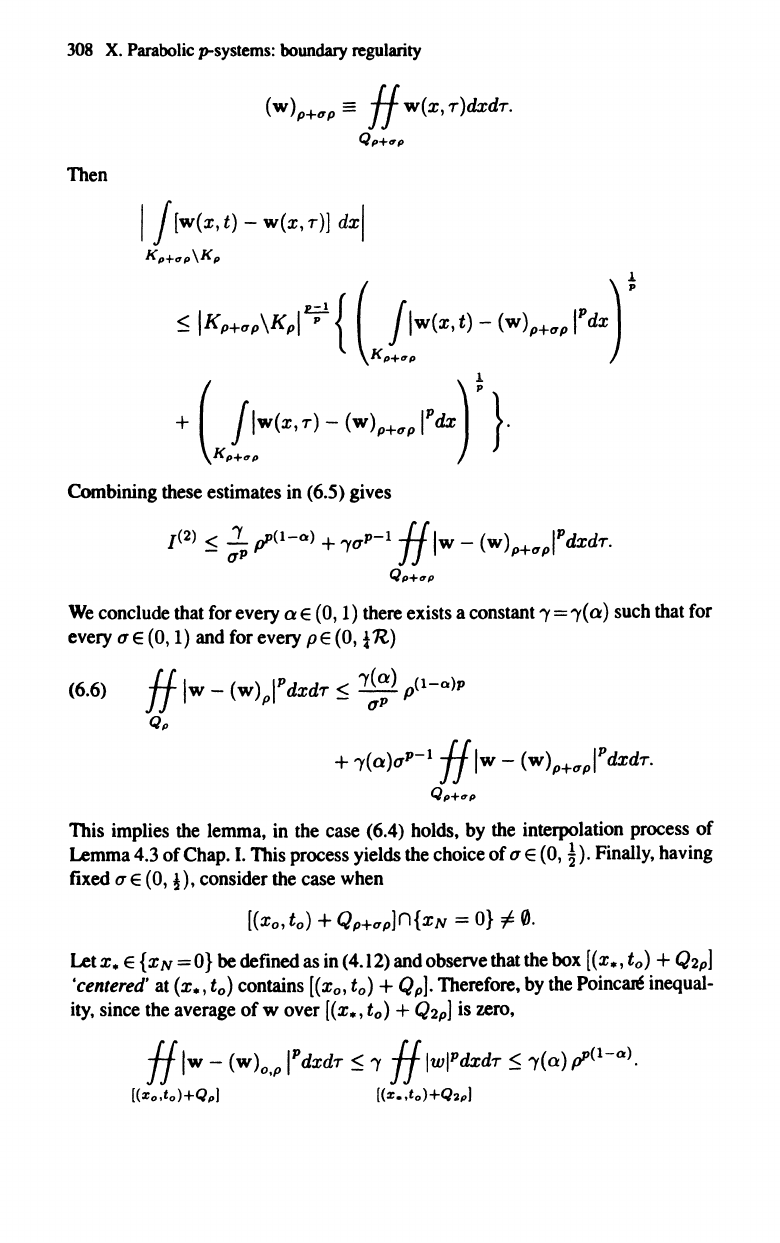
308

X.

Parabolic

p-systems:

boundary

regularity

(W)P+t7P

==

if w(x, r)dxdr.

Qp+"p

Then

I j [w(x, t) - w(x, r)]

dXI

.1

~

IKp+t7P\Kpl~

{(

jIW(X,t)

-

(w)P+t7P

1PdX)

p

Kp+"p

.1

+

L!.~w("

T)

-

(W)"..,

I'

<Ix

) ,

}.

Combining

these

estimates

in

(6.5) gives

[(2)

~

;P

,;'(1-0)

+

'Y

Up

-

1

if

IW

-

(W)p+t7pI

P

dxdr.

Qp+"p

We

conclude

that

for

every

aE

(0,1)

there

exists a constant 'Y='Y(a)

such

that

for

every

uE

(0,1)

and

for

every

pE

(0,

fR)

(6.6) if

Iw

-

(w)pI

P

dxdr

~

'Y~~)

p(l-o)P

Qp

+ 'Y(a)u

P

-

1

if

Iw

-

(w)p+t7

p

I

P

dxdr.

Qp+"p

This

implies

the

lemma,

in

the

case

(6.4)

holds.

by

the

interpolation

process

of

Lemma

4.3

of

Chap.

I.

This

process

yields

the

choice of u E

(0,

!).

Finally,

having

fixed

u E

(0,

!),

consider

the

case

when

[(X

o

,

to)

+

Qp+t7p]n{XN

=

O}

~

0.

Letx. E

{XN

=O}

be

defined

as

in

(4.12)

and

observe

that

the

box

[(x.,

to)

+

Q2p]

'centered'

at

(x.,

to)

contains

[(xo,

to)

+

Qp].

Therefore,

by

the

Poincare

inequal-

ity,

since

the

average

ofw

over [(x.,

to)

+

Q2p]

is

zero,

if

Iw

-

(w)o,p

IPdxdr

~

'Y

if IwlPdxdr

~

'Y(a),;'(l-o).

[(zo,to}+Qp)

[(z.,t

o

)+Q3p)

7. Comparing w and v 309

6-(i). Proof

of

Theorem

1.1

(the

case p>2)

The proof is a consequence

of

Lemma (6.1) and the averaging theory

of

Campanato-Morrey spaces [22,23,33,79]. It can also be proved directly, starting

from (6.2), by arguments similar to those in

§§2

and 3

of

Chap. IX.

7.

Comparing w and v (the case max

{I;

&~2}

<p<2)

Assuming that (x

o

, to)

==

(0, 0), the functions w and v satisfy

(7.1)

8

at

(Vi -

Wi)

- div

(I

Dv

I

P

-

2

DVi

-IDwl

p

-

2

DWi)

= -

!3

8

(al,k(x,

DU)Ui,Zk

-IDulp-2

Ui

,Zk

Ot,k)

uXl

- div

(lDulp-2

DUi

-

IDwl

p

-

2

DWi)

- Bi(x,

t,

w,

Dw),

in

+Q'k

Vi

-

Wi

=0,

on the parabolic boundary

of

+Q'k.

The boxes

Q'k

are formally identical to those introduced in the degenerate case

p > 2.

In

the singular case we will take

TJ

E (

-1,

0). In writing (7.1) we have used

the definitions (2.3) and (2.8). From

(2.3)-(2.4)

we derive the estimate

lal,k(x,

DU)Ui,ZI

-IDulp-2

Ui

,ZI!

$

-yR)..IDulp-l,

i=1,2,

...

,m,

l,k=1,2,

...

,N.

Moreover by Lemma 4.4

of

Chap. I,

IIDuIP-2Dui

-IDwlp-2Dwil

$

-ydD(u

-

w)I

P

-

1

$-y,

since the boundary data g are regular. In the weak formulation

of

(7.1) we take the

testing functions

Vi

-

Wi

modulo a Steklov averaging process, integrate over +

Q'k

and add over i = 1, 2,

...

,

m.

Using the remarks above to estimate the correspond-

ing terms

on

the right hand side gives

(7.2)

//(11ID

(sv +

(1-

s)w) I

P

-

2

dS)

IDw

-

Dvl2

dxdr

+Qk

$

-yR)..

/

/IDuIP-1IDW

- nvl dxdr

+Q~

+

-y

/

/IDW

- Dvl dxdr +

-y

//IBIIW -

vi

dxdr.

+Q~

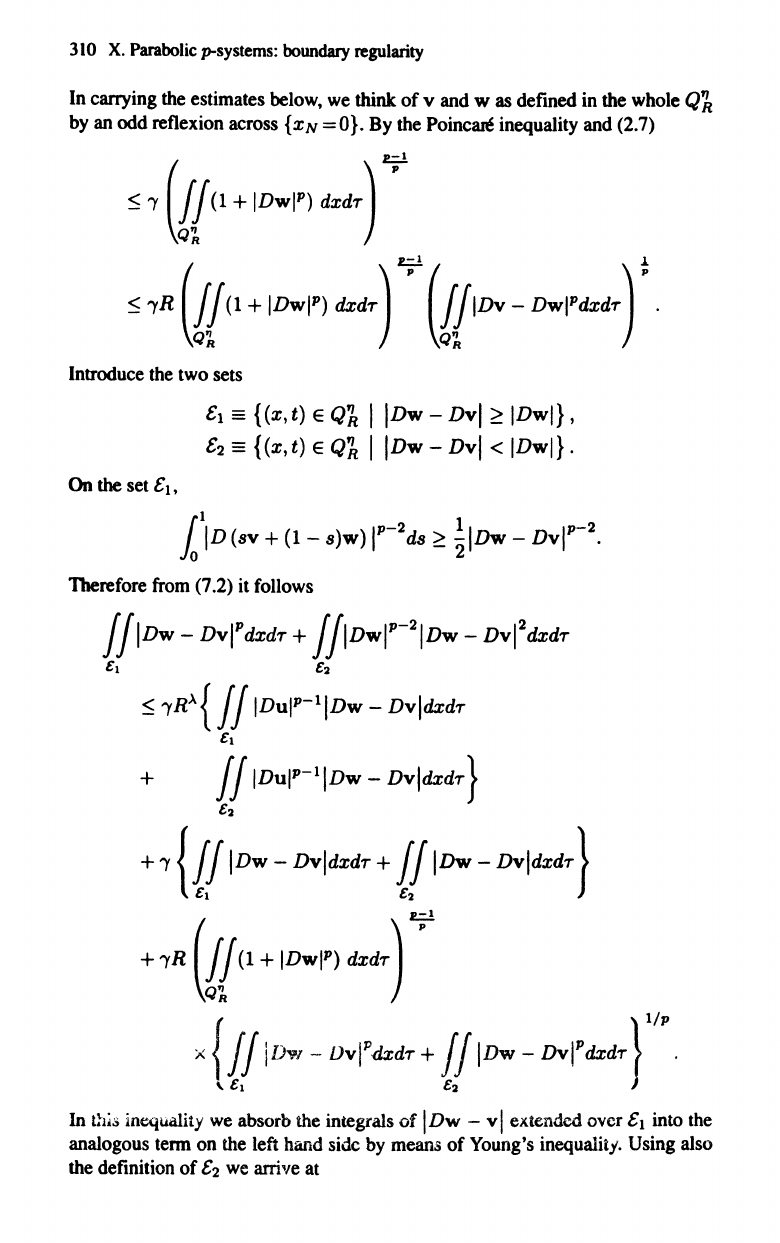
310

X.

Parabolic:

p-systems:

boundary

regularity

In

carrying

the

estimates below,

we

think

of

v and w as defined

in

the whole

Q'k

by

an

odd reflex

ion

across

{ZN

=O}. By

the

Poincare inequality and (2.7)

2::!

$

~

([[<1+

IDwIP)

dxdT)

·

2::!

.1

$

~R

([[<1+

IDwIP)

dxdT)

· ([[IDv -

DwIPdxdT

r

Introduce

the

two sets

£1

==

{(z,t) E

Q'k

IIDw

-

Dvl

~

IDwl}

,

£2

==

{(z,t) E

Q'k

IIDw

-

Dvl

<

IDwl}·

l11D

(sv

+

(1

-

s}w)

I

P

-

2

ds

~

~IDW

-

DvIP-2.

Therefore

from

(7.2) it follows

!!IDw

- DvlPdxdr+

!!IDWIP-2IDw

- Dvl2dxdr

£1 £2

:5

'YR'>'{!!

IDuIP-1IDw

- Dvldxdr

£1

+

!!

IDuIP-IIDw

-

Dvldxdr}

£2

+

~

{

[/

IDw

-

Dvld%dr+

[f

IDw

-

Dv1dxdT}

2::!

+

~R

([[<1+

IDwIP)

dxdT)

·

"

{J

J i

Dw

-

Dvl

P

dxdT+ //IDw -

DvI

P

dxdT}

IIp

\

£1

£2

In

t~l~"

inequality

we

absorb the integrals

of

IDw

-

vi

extended over

£1

into

the

analogous term on

the

left hand side

by

means of Young's inequalitj. Using also

the

definition of

£2

we

arrive at

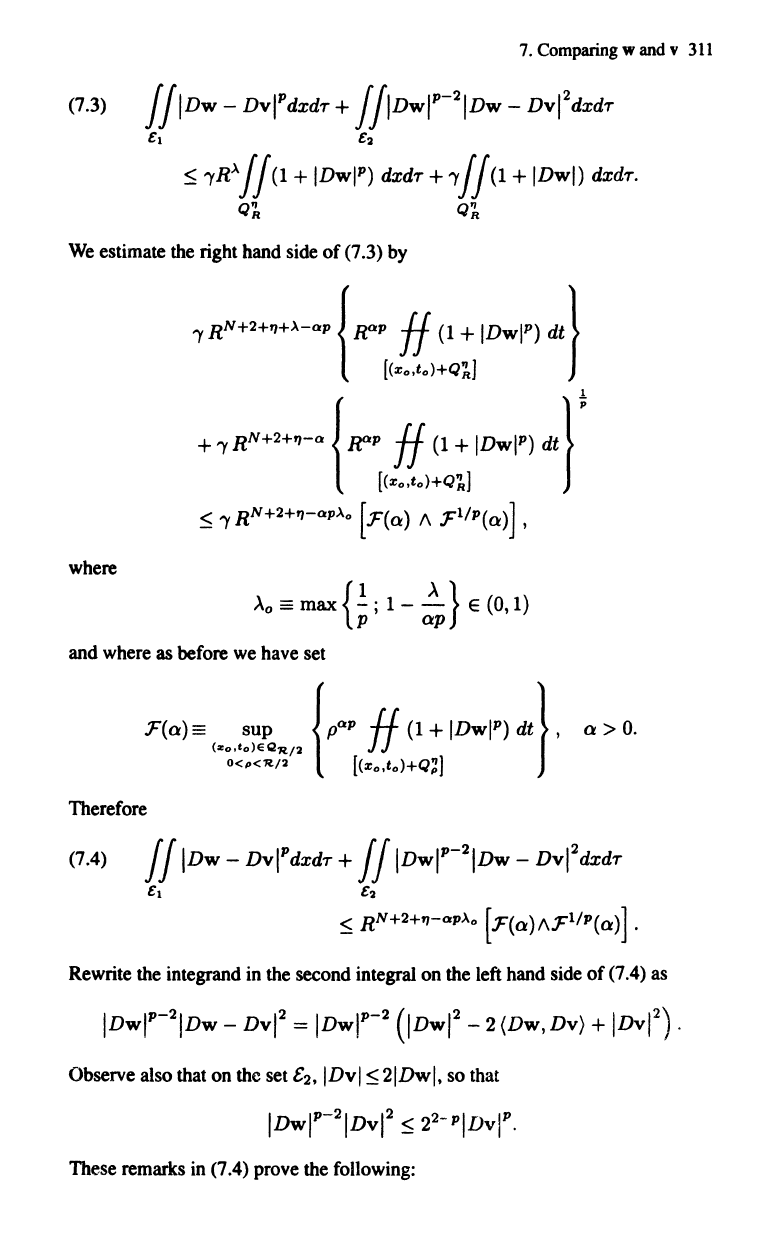
7. Comparing w and v

311

(7.3)

!!IDW

-

DvlPdxdr+

!!IDwIP-2IDW

- Dvl2dxdr

£1

£2

$

'Y

R

>..JJ(l

+

IDwI

P

)

dxdr +

'Y!J(l

+

IDwl)

dxdr.

Q~

We

estimate

the

right hand side of (7.3)

by

'Y

R

N

+

2

+'1+>"-OP

{nap

H

(1

+

IDwI

P

)

dt}

[(Zo.to)+Q~l

1

+

'Y

RN

+2+'1-

0

{nap

H

(1

+

IDwI

P

)

dt}

P

[(zo.to)+Q~l

$

'Y

R

N

+

2

+'1-

o

p>"o

[.r(a)

A

.r1/P(a)]

,

where

~o=max{!;

1-~}

E(O,l)

P

ap

and where

as

before

we

have set

Therefore

(7.4)

J J

IDw

-

Dvl

P

dxdr

+ J J

IDwIP-2IDw

-

Dvl2

dxdr

£1

£2

$ R

N

+

2

+'1-

o

p>"o

[.r(a)A.r1/P(a)]

.

Rewrite

the

integrand

in

the second integral

on

the left hand

side

of

(7.4)

as

Observe also that on the set E

2

•

IDvl

$

21Dw

I.

so that

IDwIP-2IDvI2

$

22-PIDvIP.

These remarks in (7.4) prove

the

following:

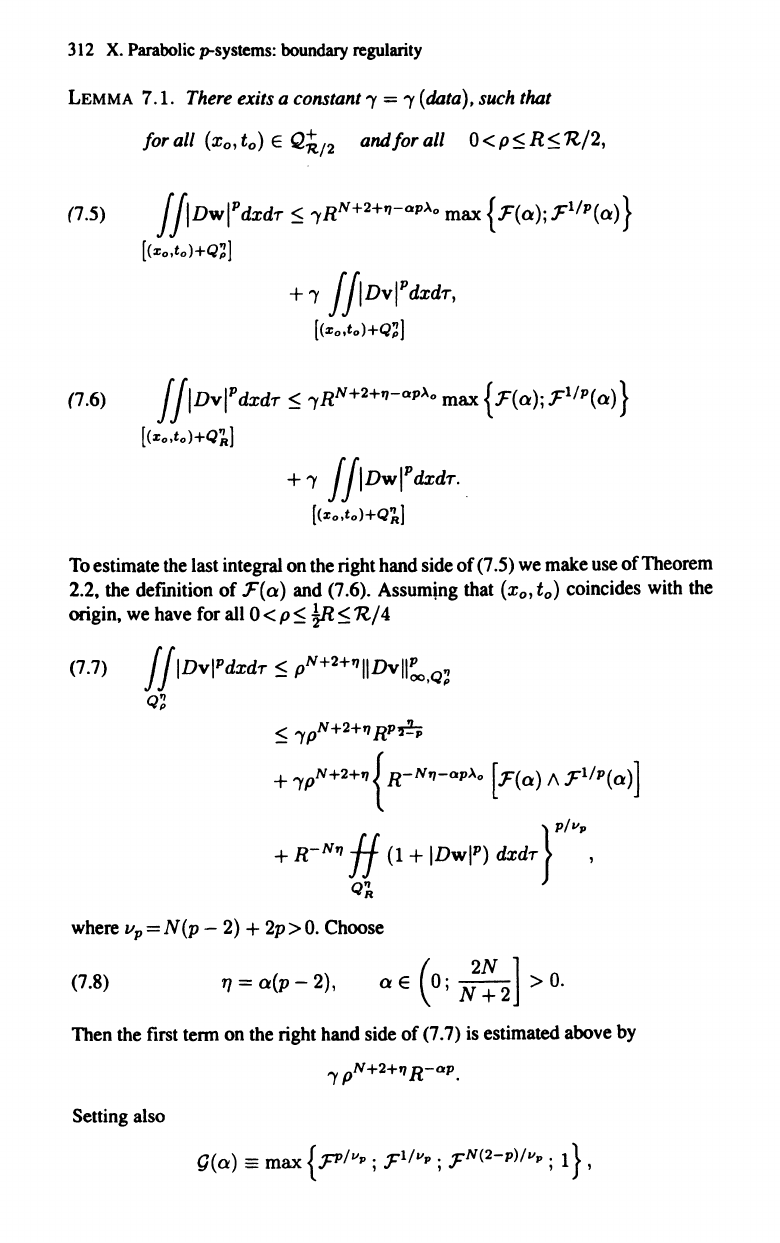
312

X.

Parabolic p-systems: boundary regularity

LEMMA 7.1. There exits a constant

'Y

=

'Y

(data), such that

forall

(xo,t

o

)

E Q:k/2

andforall

O<p5,R5,'R/2,

(7.5)

jjlDwlP

dxdT

5,

'YR

N

+

2

+'1-

o

p>,0

max

{F(Q)j

F1/P(Q)}

[(xo,to)+Q~1

+

'Y

j

jlDvlPdxdT,

[(xo,to)+Q~1

(7.6) j

jlDvlP

dxdT

5,

'YRN+2+'1-op>,o

max

{F(Q)j

Fl/p(Q) }

[(

Xo

,to)

+Q7t1

+

'Y

j

jlDwlP

dxdT

..

[(xo,to)+Q~1

To

estimate

the

last integral on the right hand side

of

(7

.5)

we

make

use

of

Theorem

2.2.

the defmition

of

F(Q) and (7.6). Assuming that (xo, to) coincides with the

origin, we have for all 0

< p

5,

!R

5,

'R/4

(7.7) j jlDvlPdxdT

5,

pN+2+'1I1DvIl:O,Q~

Q~

5,

'YpN+2+'1RP~

+

'YPN+2+'1{

R-N'I-op>'o

[F(Q) "

F1/P(Q)]

}

PIlip

+ R-N'I H

(1

+

IDwl

P

)

dxdT ,

Q7t

where

lip

=

N(p

- 2) + 2p >

O.

Choose

(7.8)

11

= Q(p -

2),

Q E

(0

j

;:2]

>

O.

Then the first term on the right hand side

of

(7.7)

is

estimated above by

'Y

pN

+2+'1

R-oP.

Setting also

9(Q)

==

max

{pilip

j

Fillip

j F

N

(2-p)/lI

p

j

I}

,

8.

Estimating

the

local

average

of

IDwl

313

the

second

term

on

the

right

hand

side of

(7.7)

is

estimated by

-yQ(a)

(~)N+2+'1//(1

+ IDwI

P

)

dxdr

Q1t

+

-yQ(a)

pN+2+'1

R-(N'1+

2a

p>.o)p/"p.

Using

the

dermition (7.8) of

1]

we

have

p

ap2

-(N1]

+ 2apA

o

)-

=

-a

+

-(1

-

Ao).

lip lip

Since

~oE

(0,1)

we

estimate R-(N'1+

a

p>.o)p/"p

~

R-ap,

and

summarise:

LEMMA 7.1. Let a and

1]

be

chosen

as

in

(7.8).

There

exists a

constant

-y

=

-y(data),

independent

of

a,

1],

p,

R,

such

that

forall (xo,to) E

Q:k/2

andforall

0<p~R~n/2,

(7.9)

//(1

+ IDwlP)dxdr

[(xo,to)+Q~J

~

-yQ(a)

(~)N+2+'1

//(1

+ IDwlP)dxdr

[(x

o

,t

o

)+Q1tJ

+ -yQ(a)

pN+2+'1R-

a

P.

8.

Estimating

the

local average of

IDwl

LEMMA 8.1.

For

every

a E (0,1)

there

exists a constant

-y

=

-y

(a,data),

such

that

forall (xo,to) E Q:k/2 andforall

0<p~R~n/2,

(8.1) H

(1

+ IDwI

P

)

dxdr

~

-y(a,data)p-a

p

.

[(xo,to)+Q~J

PROOF:

Derme

sequences

ao=(N

+

2)/2

and

forn=O,

1,2

...

,

1]n

=

an{p

-

2),

314 X. Parabolic p-systems: boundary regularity

It

is

apparent that {on},

{l1n},

{On}

-+

0

as

n

-+

00.

We

will

prove

by

induction

that

(S.2)

F(on)

:5

')'n

(on. data) , n =

0,

1,2,

....

Since

IDwleLP(lh),

H

(1

+ IDwI

P

)

dxdr:5

')'p_P(~+3)

(1

+ IIDwllp,SlTt.

[(:r:o,to)+Q~o

I

Therefore

F(oo)

:5

')'0

==

(1

+ IIDwllp,SlTt·

Assume

now

that (S.2)

holds

for

some

n and let

us

show

that it continues

to

hold

for

n +

1.

We

apply

the

iterative

Lemma

3.1

with

the

choice of

the

parameters

to

the

function

(3

==

N + 2 +

l1n,

" = onP, 0 =

on,

1/

=

0,

<p(p)

= II

(1

+ IDwI

P

)

dxdr,

1(:r:o,to)+Q~n

I

which

satisfies (7.9),

to

conclude that for

all

(xo,

to)

e Q:k/2

and

for

all

0 < p:5

R:5'R/2,

In

particular, p being

fixed,

(S.3)

must

hold for radii

p.

satisfying

Without

loss

of generality

we

may

assume

that

"',,-'Intl

2+'In+1

_ D

p.

= (;.

is

an

integer.

Then

we

may

regard

the

cube

Ixo

+ K

pI

as

the

disjoint

union,

up

to

a

set

of

measure

zero,

of

(f..)N cubes Ix; +

Kp.1

centered at points

x;

of

[xo

+

Kpl.

Similarly

we

regard

the

cylinders [(x

o

•

to)

+

Q~n+l]

as

the

disjoint

union,

up

to a set of

measure zero,of(i.)N cylinders

[(x;,

to)

+

Q::].

We

write (S.3)

for

each

of these

cylinders

and

add

up

for j =

1,

2,

...

,i.

to obtain

II

(1

+ IDwI

P

)

:5

')'

(i.)N

p~+2+"n-anp+6n

1(:r:o,to)+Q:n+l1

9.

Bibliographical

notes

315

Therefore

pQ

n

+1P

H

(1

+

IDwI

P

)

dxdr5,'Y

and

F(a

n

H,1Jn+t}

5,

'YnH'

[(:l:o,t

o

)+Q:n+1]

8-(1).

PROOF

OF THEOREM 1.1 (THE CASE max

{I;

~~2}

< p <

2)

By

a cube decomposition technique similar

to

the one outlined,

Lemma

8.1

can

be

rephrased

in

tenns of the parabolic cylinders Qp=Q(p2,

p).

LEMMA 8.1'. For every a E (0,

1)

there

exists a constant

'Y

=

'Y

(a, data),

such

that

(8.1)' H

(1

+

IDwI

P

)

dxdr

5,

'Y(a,data)p-QP.

[(:l:o,to)+Qp]

With

this lemma at hand the proof is

now

concluded

as

in the degenerate case.

First

we

may

establish a version of Lemma

6.1

and

then the

HOlder

continuity of u

follows

from

the

arguments

of

[22,23.32,79] or

by

those in

§§2

and 3 of

Chap.

IX.

9. Bibliographical notes

The proof of Theorem

1.1

is

in

[27].

The iteration Lemma

3.1

is

in

the

same

spirit of

DiBenedetto E. Degenerate Parabolic Equations

Подождите немного. Документ загружается.