DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


326
XI.
Non-negative
solutions
in
I:T.
The
case
p>2
Combining these estimates in (5.6),
(5.7)
where
we
have changed pinto
2p.
Next, for all
'1
~
t
~
T-e
6.
Uniqueness for data
in
Lloc(RN)
THEOREM
6.1.
Letu
and v be two non-negative local weak solutionsof(l.5) in
ET. satisfying
Then
u==v
in
ET.
PROOF:
Fix
r>O
and some
eE
(0.
T)
and set
Ilullr.T-~
+
Ilvllr.T~
==
A.
Then and u and v satisfy all the estimates
of
Theorem
2.1
with
the
quantities
llu.
vllr.T~
replaced by A within the strip
ETa'
where
0<
To
= min{T;"Y.A-(p-2)}.
and
"Y.
is
the constant appearing in (2.5). It will suffice to prove uniqueness within
the strip
ETa'
The difference
w=u-v
satisfies

(6.1)
where
6.
Uniqueness
for
data
in
LJ.,..(R
N
)
327
a'J(z,
t)
=
(iiD(B.
+
(1
-
B)_)iP-'ds)
6,;
1
+ (p - 2) j ID(su +
(1
- s)v)IP-4
o
X
(su
+
(1
- s)v)x.
(su
+
(1
-
s)v)xjds.
The
matrix (ai,i)
is
positive semi-definite
and
for
all
e E RN
and
(x, t) E
ETo
{
ao(x,
t)lel
2
l
S ai,i (x, t)eiei S (p -
l)a
o
(x,
t)leI
2
,
(6.2)
ao(x, t) =
flD(su
+
(1
- s)v)IP-
2
ds, (x,
t)
E
ETo'
o
Let
Ao(x)
be
the
weight introduced
in
(5.1)
with
a satisfying (5.2).
In
the
argu-
ments
below,
-y
denotes
a positive constant that
can
be
determined a priori
only
in
terms
of N,
p,
u
and
A.
6-0). Auxiliary
lemmas
LEMMA 6.1. There exists a constant-Y='Y(N,p,u,A) such that ifw(" t)-+O in
Lloc(RN) as
t'.,O.
then
j1w(x,
t)IAa(x)
dx
S
-yt
l
/",
0<
t <
To.
RN
PROOF:
The
functions w±
are
both
weak
subsolutions of (6.1), i.e.,
wr
-(ai'i(x,
t)w~)x.
SO
weakly
in
ETo'
,
By
working
separately
with
w+
and
w-
we
may
assume
that w
is
a
non-negative
subsolution of (6.1).
In
the
weak
formulation of (6.1)
take
the
test
function
x-+
Ao(x)«x),
where
(is
the
usual
cutoff
function
in
Kp.
Using
the
assumptions
of
the
lemma
we
deduce
t
j1w(x,
t)IAo(x)(
dx
S
'Y
j
j(/DV/
+
/Dv/y-I/DA
o
(/
dxdr
Kp OKp
t
S
'Y
j
j(lDV/
+
/DvD,,-1
AoID(1
dxdr
OKp
t
+-y j
j(lDvl
+
IDvD,,-IIDAoldxdr.
OK,.

328
XI.
Non-negative
solutions
in
ET.
The
case
p>2
In the last
integral.IDAal
$'YAa+l/p
and in the first integral. since
IDcl
=0
on
Kp/2
we have AalDCI
$'YAa+l/p
for p >
1.
Therefore letting p-+oo
t
jlw(x.t)IAa(X)dX
$
'Y
jjODvl
+
IDvI)P-l
Aa+l/pdxdr,
RN
ORN
and the conclusion follows from Theorem 5.1.
PROOF: Let
fiE
(0,
*,)
be fixed. Then
'v'tE
(0,
To)
j1w{X,
t)
I 1+'1 A
a
+
fJ
/(p-2)
{x)dx
RN
$
jIW{X,
t)l
fJ
A
fJ
/(p-2)
{x)lw(x,
t)IAa{x)dx.
RN
By
(5.5).lw(x,
t)lfJA
fJ
/(p_2)
(x) $
'Yt-If
'I.
so that by Lemma 6.1.
jIW(x,
t) I 1+'1 A
a
+
fJ
/(p-2)
{x)dx $
'Yc
IYf
j1w(X,
t)IAa{x)
dx
RN
RN
$ 'Yt!
(l-NfJ).
6-0;). Proof
of
Theorem
6.1
In (6.1) we may assume. by working separately with w+ and
W-.
that w
~
O.
In its
weak:
formulation we take the testing functions
Integrating over
K p x
(c,
t). 0 < C < t $
To.
we obtain
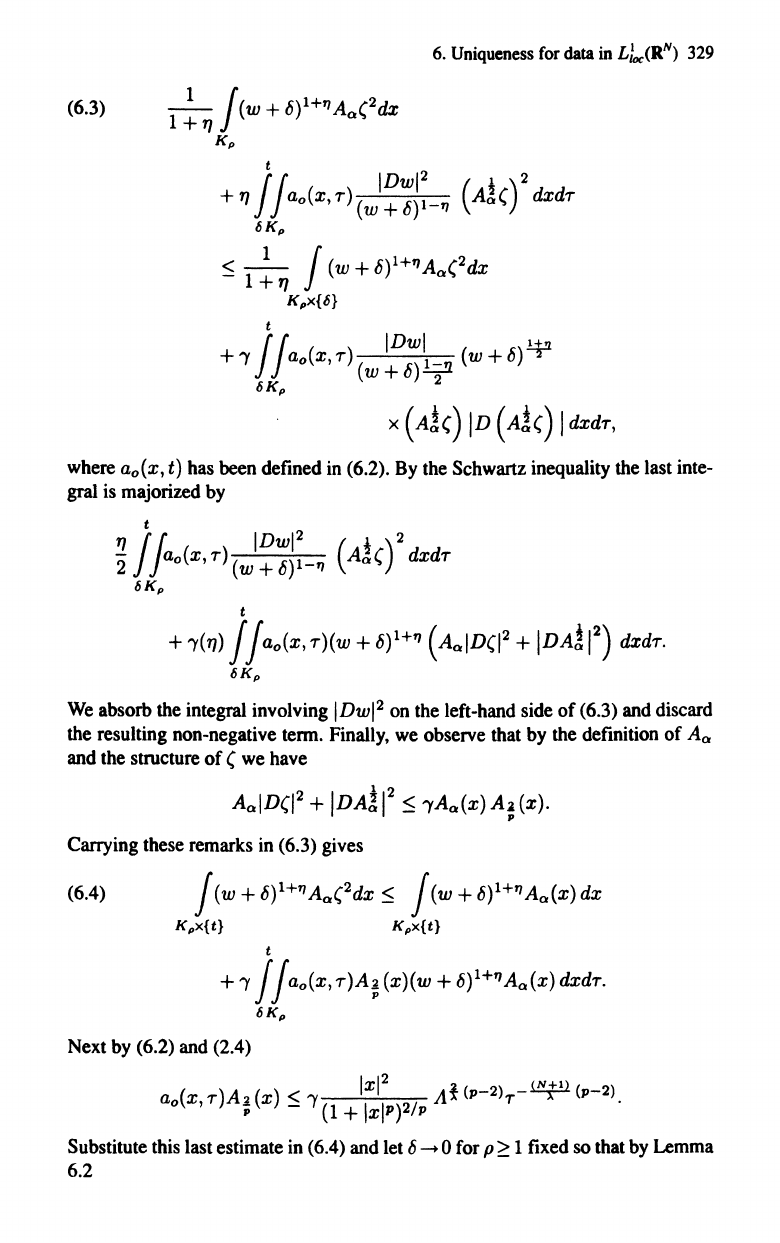
6.
Uniqueness
for
data in L:""(R
N
)
329
(6.3) 1
~
11
!(W
+
6)1+'7AQ(2dx
Kp
t
If
IDwI2
(1)2
+11
a
o
(x,r)(W+6)1-'7 A
Q
(
dxdr
6K
p
~
1
~
11
!
(w
+
6)1+'7AQ(2dx
Kpx{6}
t
+'1
!!ao(X,r)(W~~~
(w+6)l:f1
6K
p
X
(A!()
ID
(A!()
I dxdr,
where ao(x, t) has been defined in (6.2). By the Schwartz inequality the last inte-
gral is majorized by
t
+
'1(11)
!
!ao(x,
r)(w +
6)1+'7
(A
Q
ID(1
2
+ IDA!
12)
dxdr.
6K
p
We absorb the integral involving
IDwl2
on the left-hand side
of
(6.3) and discard
the resulting non-negative term. Finally, we observe that by the definition
of
AQ
and the structure
of
( we have
A
Q
ID(1
2
+ IDA!
12
~
'YAQ(X)
Al
(x).
p
Carrying these remarks in (6.3) gives
(6.4)
!(w
+
6)1+'7AQ(2dx
~
!(w
+
6)1+'7AQ(x)
dx
Kpx{t} Kpx{t}
t
+'Y!
!ao(X,r)A;(x)(w
+ 6)1+'7AQ(x)dxdr.
6K
p
Next by (6.2) and (2.4)
a (x r)A.a(x) <
'1
Ixl2
Ai
(p-2)r-(Nr>
(p-2).
0,
p -
(1
+
Ixl
p
)2/p
Substitute this last estimate in (6.4) and let 6 - 0 for p
2:
1 fixed so that by Lemma
6.2

330 XI. Non-negative solutions
in
ET.
The case
p>2
j (w + 6)1+f/Ao(x)dx
--+
°
as
6 - 0.
Kpx{6}
Then we let p -
00.
The net result is
j1w(x,
t)
1
1+'1
Ao(x)
dx
RN
t
:5
'Y
j.,.-
(Ntl)
(p-2)
j1w(x,
"')11+'1
Ao(x)
dxd.,..
o
RN
Since.,.-
(Nti)
(p-2)
E
L1
(0, t), this implies
t-
j1w(x,tW+f/Ao(X)dx
==
0,
RN
by Gronwall's lemma, provided
t-
/lw(x,tW+f/Ao(X)dX
E VlO(O,T
o
)'
RN
Now the parameter Q in the calculations above is arbitrary and only restricted by
(5.2).
If
Q is replaced by
Q+,,/(p-2).
then Lemma 6.2 and its proof ensure the
Loo(O,
To)
requirement and the theorem follows.
Remark
6.1. For non-negative solutions u and v
of
(1.5) in ET. the quantities
(6.5)
Ilullr,T-E,
IIIvllr,T_
are fmite.
The proof
of
Theorem 6.1 uses only this information. Indeed by Remark 2.2 such
a growth condition implies all the estimates
of
Theorem 2.1. We conclude that
the uniqueness theorem for initial data taken in the sense
of
Lloc(RN) holds for
solutions
of
variable sign provided (6.5) holds.
7. Solving the Cauchy problem
Consider the Cauchy problem
{
u
E C
(0,
T;
Lloc(RN»nLfoc
(0,
T;
W,!;:(RN») ,
p>2,
(7.1)
Ut
-
div
(lDulp-2Du) = ° in ET, for some
T>O
u(·,O) = U
o
E Lloc(RN).
As indicated in the firstof(7.1) the initial datum is taken in the sense
of
Lloc(RN).
By Theorem 6.1 and Remark
6.1
there is at most one solution
to
(7.1) within the
class
of
functions u satisfying

7.
Solving
the
Cauchy
problem
331
(7.2)
Ilullr,T-£ <
00
for
some
E E (0, T).
Existence of a solution satisfying
(7.2)
can
be
established if
the
initial datum U
o
satisfies
the
growth
condition
- f
luo(x)1
(7.3)
Iluoli
r
=
:~~
P"/(p-2)
dx<oo,
for
some
r >
O.
Kp
Since U
o
ELloc(RN) if
Iluollir
is
finite
for
some
r
>0,
it
is
finite
for
all r>O.
THEOREM
7.1. Let U
o
satisfy (7.3) for
some
r >
O.
There
exists a
constant
'Y.
=
'Y.(N,p)
such
that
defining
(7.4)
there
exists a
unique
solution
u
to
(7.1)
in
ET.
Moreover
u satisfies (7.2) for all
eE(O,
T)
and
the
estimates (2.2)-(2.4)
of
Theorem
2.1.
Remark
7.1.
This
is
an
existence
theorem
local
in
time
and
the
largest existence
time
is
estimated
by
(7.4). The functional dependence
in
(7.4)
is
optimal
as
shown
by
the
following
explicit solution.
{
(
T
)~
(p
-
2)
_~
(
Ixl
P
)p!r}~
1'(x,t)=
A
--
+
--
..\
p=-r
--
,
T-t
P
T-t
where
A
and
T
are
two
positive parameters.
By
direct calculation
we
have
~
~111>(.,O)llr
=
~
(P;2)P-
("\T)-~,
where
W N
is
the
area of
the
unit sphere
in
R
N.
Therefore 1'( x, t) exists
up
to
the
blow-up
time
{
}
-<P-2)
T =
'Y.
~
1111>(·,OHlr
,
where
'Y.
=
..\-~
(~r-2
(p;
2)P-l
For
n=
I,
2,
...
,consider
the
sequence of truncated initial data
(
)
=
{max{-n;
min{uo(x);n}},
uo,n
x -
0,
It
is
apparent that
for
all
n=
1,
2,
...
,
(7.5)
Consider also
the
family
of approximating problems
for
Ixl
< n
for
Ixl
~
n.

332
XI.
Non-negative
solutions
in
Er.
The
case
p>2
{
Un,t
- div
IDUnl
p
-
2
Du
n
= 0,
in
RN
xR+
un(·,O) = uo,n·
Since
uo,n
are compactly supported in
RN,
(7.1)n can
be
uniquely solved
as
indi-
cated
in
§12
of Chap.
VI.
By
the maximum principle the solutions Un are bounded
by
n.
Therefore the quantities
III
III
-
!un(X,
'T)
unl
r,t
= sup sup
P>-/(
-2)
dx
O<.,.<tp>r P
- Kp
are finite for all
r,
t >
o.
It follows that the sequence
{Un}
satisfies (2.2)-(2.4)
of
1beorem 2.1.
We
will
tum
such n-dependent information into a quantitative sup-
estimate
of
{un}
independent
of
n. Let x --+
,(X)
be
the standard cutoff function
in K
2p
•
Then (7.1)n implies
We
divide
by
p>'/
(p-
2) and take the supremum over all
p>
r. Taking into account
(7.5) and (2.3) this gives
for two constants
'Yi
='Yi(N),
i=O,
1.
Let
tn
be
defined
by
(
P-2)
1/>.
1
'Yl
tn
Ilunllr,t
=
2·
Then from (7.6) for all t E (0, t
n
)
IIlunllr,t
~
2'Yo
Iluoli
r.
This implies that
tn
~
Tr for all n =
I,
2,
...
" where Tr
is
defined
by
We
summarise:
LEMMA
7.1.
Let
{Un}
be
the
sequence
of
the
approximating
solutions
(7.1)n.
There
exists
a
constants
'Y
= 'Y(N,p) and
'Y.
= 'Y.(N,p)
independent
ofn.
such
that
(7.7)
where
(7.8)

8.
Bibliographical
notes
333
Given such an estimate, the Cauchy problem (7.1) can be solved by a standard
limiting process. Indeed by Theorem 2.1 the sequences
{
f)
}
-Un
,
f)xi
nEN
i =
1,2,
...
,N,
are locally equibounded and equi-HOlder continuous in
RN
x (0, Tr). This gives
the existence
of
a unique solution in ET
r
•
The
largest time
of
existence can be
calculated from
(7.8) by letting r
-+
00.
In particular the solution to (7.1) is global
in time
if
. j uo(x)
lim
sup
>./(
-2)
dx =
O.
f'-OO()
p>r P P
Kp
8. Bibliographical notes
Theorem 2.1 is taken from [41]. A weaker version
of
(2.2) in
I-space
dimension
is due to Kalashnikov [58]. It is remarkable that in
(2.4) one can also control the
behaviour
of
the space-gradient IDul as Ixl-+
00.
Since IDul
2
is a non-negative
subsolution
of
a porous
medium-type
equation (see (1.8)
of
Chap. IX) the same
techniques yield a version
of
(2.2) for such degenerate p.d.e. The analog
of
(2.2)
for the porous medium equation is due to
Benilan-Crandall-Pierre
[10] in the
context
of
an existence theorem. A rather general version is in [4]. Perhaps the
most relevant estimate
of
Theorem 2.1 is the integral gradient bound (2.3) proved
in [41]. A version
of
such a local bound, for the porous medium equation is in [4]
and reads
jlDuml
dxdr
~
-yt
1
/"p1+w!=r
"lu"I!;.:~l,
K.
=
N(m
- 1) + 2,
Kp
where -y=-y(N, m) and
- j u(x,t)
IIIulllr,T-E =
sup
sup
,./(m-l)
dx.
O<tST~p>r
p
Kp
The estimate holds for
small
time intervals and for general non-linearities.
We
refer to [4] for details. There is no analog
of
(2.4) for the porous medium equation.
Theorems 4.1 is taken from [41]. The analog for the porous medium equations is
in [6] and for general non-linearities [4]. It would
be
desirable to have a version
of
the uniqueness Theorem 6.1 for initial data measures. This would parallel the
analogous theory for the heat equation.

XII
Non-negative solutions in E
T
.
The case 1
<p<2
1.
Introduction
We
will investigate the structure
of
non-negative solutions
in
the strip ET of the
singular p.d.e.
(1.1)
Ut
- div IDulp-2
Du
=
0,
I<p<2.
A striking feature of these singular equations
is
that, unlike the degenerate case
p>2,
non-negative solutions of (1.1)
are
not restricted
by
any
'growth
condition'
as
Ixl-
00.
Nevertheless they have initial traces that
are
Radon measures.
More-
over they
are
unique
whenever the initial traces
are
in
Lloc{R
N
).
Accordingly, the
Cauchy problem for
(1.1) associated
with
an
initial
datum-
(1.2)
U
o
~O,
is uniquely solvable, regardless of
the
behaviour of
x-uo(x)
as
Ixl-oo.
The
case 1 < p < 2
is
noticeably different
from
the
case p >
2,
both
in
terms
of results
and
techniques. The
main
difference stems
from
the fact that, unlike
the
degenerate case, solutions of (1.1)
are
not,
in
general, locally bounded. In a precise
way,
if
(1.3)
and
2N
P>-N
'
+r

1.
Inttoduction
335
then the solution
'1£
of (1.1)-(1.2) belongs
to
Lroc{ST)
,
"It>
O.
This
is
the
content
of
Theorem
5.1
of
Chap.
V.
In
§
13
we
will
give a counterexample that
shows
that
if
'1£0
violates (1.3),
then
'1£
¢
L~c{ET).
The
basic formal energy estimate
for
(1.1)
is
VO<8<t~T,
VKp
t
(1.4) sup
ju
2
{x,
r) dx + f flDulPdxdr
s<r<t
11
- -
Kp
sKp
Thus
ifu
e
L~oc{ET),
the
left
hand
side of (1.4)
is
finite
and
IDul
e
Lfoc{ET)'
However if
'1£0
e Ltoc{RN), there
is
no
a priori information
to
guarantee that
(1.5)
We
have
spoken
oholutions of (1.1); however if (1.5)
fails,
one
of
the
main
prob-
lems
is
to
make
precise
what
it
is
meant
by
solution.
Thus
the
starting point of
the
theory
is
to
give a precise
meaning
to
Du
to
make
sense
out of
(1.1). The
previous
remarks
suggest
that
IDul might fail
to
be
in
Lfoc{E
T
),
roughly speaking
at
those
points
where
'1£
is
unbounded.
Motivated
by
these
remarks,
we
have
given
a
novel
formulation of non-negative
weak
solutions.
Such
solutions
are
'regular'
in
the
sense that
the
truncations
(1.6)
Vk
>
0,
Uk
= min{u, k},
satisfy
(1.7)
Then
(1.1)
can
be
interpreted
weakly
against testing functions
that
vanish
'when-
ever
'1£
is
large'. A suitable choice of
such
testing
functions
is
(~-
'1£)+
==
max{(~
- u);O},
~
e
C~{ET);
ET'
The
notion
is
introduced
and
discussed
§§2
and
3.
We
prove
that
these
solutions
coincide
with
the
distributional
ones
if
(1.5)
holds
and
that
the
truncations
Uk
are
distributional
super-SOlutions
of (1.1)
Vk
>
O.
We
derive
a spectrum of properties
of
such
local
weak
solutions, regardless of their initial
datum.
In
particular
we
investigate
the
behaviour of
DUk
as
k
-+
00.
A relevant
fact
is
the estimate
(1.8) frlDulP-l dxdr
~
"Y
sup
fu{x,
r) dx +
"Y
(t
-"s)
~
,
11
s<r<t
P
BKp
- -
K2P
VO<8<t~T,
VK2p,
