DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


336
XII.
Non-negative solutions
in
E
r
. The case
l<p<2
where
A=N(p-
2) + P and 'Y='Y(N,p).
We
remark that in Chap. XI an estimate
of
the local integral
nonn
of
IDuI
P
-
1
was crucial to establish the existence
of
initial traces. In the singular case 1 < p < 2 it is precisely (1.8) that pennits one to
prove an integral Harnack-type inequality, which
in turns implies the existence
of
initial traces. The estimate (1.8) is essential also for the solvability
of
the Cauchy
problem.
A solution to (1.1)-(1.2) is constructed by using the increasing sequence
{ u
o
, n}
of
approximating initial data
(1.9)
Uo,n
=
min{u
o
;
n},
n = 1,2,
...
,
and solving the approximating problems
(1.10)
{
Un
E C
~O,
T;
L~o;~:N»nLP
(~,T;
WI~:(RN»)
,
Un,t
-
dlV
IDunl
DUn
= 0, lD ET,
un(·,O)
= u
o
.
n
, in the sense
of
Lloc(RN).
The comparison principle and (1.8) yield the Lloc(ET) convergence
of
the approx-
imating solutions
{un}. A one-sided bound
on
uo,n
and hence on
Un
is crucial to
this process in view
of
the regularising effect
of
Proposition 6.1
of
Chap. VI.
In
§5
we show uniqueness
of
weak solutions
if
they take their initial datum
in
the
sense
of
LloAR
N
).
Namely,
if
U and v solve
(l.l)
weakly and
if
t
-+
(u - v)(t)
-+
0, in Lloc(RN) as
t'\,O,
then the difference w = U - v satisfies
(1.11) j1w1q(t)dx
~
'Y(q)
(
N(P~2!+pq)
r-;;
,
Yq
~
1, "It > 0,
Yp
> 0
Kp
P q
for a constant
'Y
=
'Y(
N,
p,
q). The theorem follows by letting p
-+
00
after we
choose
q so large that
N(p
- 2) + pq>O.
If, in (1.3), T = 1 and
p>
~~
l'
the existence and uniqueness theory remains
valid
if
U
o
E
Ltoc
(RN)
with no sign restriction. Indeed in such a case the sequences
are locally equibounded and equi-HOlder continuous in
ET.
If
1 < p <
~~2'
the singular equation (1.1) is not fully understood. For ex-
ample it would
be
of
interest to investigate questions
of
existence and uniqueness
for the Cauchy problem
(1.1
)-( 1.2)
if
the initial datum is a measure
JL.
Finally, we
notice that all the results
of
this chapter hold true for equations
of
the type
N
Ut
-
L(lu
x
;IP-2
ux
;)x,
= 0
i=l

2.
Weak
solutions
337
2.
Weak
solutions
A measurable function U :
ET
-+
R + is a local weak solution
of
(1.1) in
ET
if
(2.1)
uEC(O,T:Lloc(R
N
)),
!DUk!ELfoc(ET), :tUkELloc(ET)
for all k>O
and'Vep
E Cgo(E
T
),
(2.2) !!{Ut(ep -
u)+
+
IDuIP-
2
DuD(ep
- u)+}dxdr =
o.
ET
Introduce the spaces
(2.3)
(2.4)
Xl
oC
(ET)
==
{ep E Xloc(ET) ! ep(x,t) = 0,
'Vlxl
>
p}.
'Vt
E (0, T), for some p > 0
o
By density, (2.2) holds for all
ep
E X
loc
(ET). We denote with S the set
of
all
non-negative local weak solutions
of
(1.1) in ET.
LEMMA 2.1. Let UES. Then 'V"pEXloc(ET) and
'V'TlE
Cgo(ET).
(2.5) ! !{Ut("p -
u)+'Tl
+
IDul
p
-
2
DuD[("p
-
u)+'Tl)}
dxdr =
o.
ET
PROOF:
Let
/C
c
/C'
be
compact subsets
of
ET
such that
dist
(8/C,
8/c') = d > 0
and let
(E
Cgo(/C')
be
such that 0
~
(~
1 and
(==
Ion
/C.
Choose
"p
E Xloc(ET)
and in (2.2) take
where
(2.6)
'Tl
E
C;:"(/C)
and k =
1I"plloo,K:/.
We
have a.e. in
/C'\/C
Moreover
(ep
-
u)+
=
(("p
-
u)+'Tl
+
Uk(
-
u)+
=
(Uk(-U)+
=0.
(ep
- u)+ =
(("p
-
u)+'Tl
+
Uk
- u)+, a.e. in
/C.
This vanishes unless U
<"p.
In such a case,
Uk
= U and
a.e. in
/C.

338
xn.
Non-negative
solutions
in
Er. The
case
I <p<2
We
conclude that this holds a.e. in
I:T
and (2.5) follows.
Let
(f
E (0, 1) and let x - «
x)
denote the standard cutoff function in K p that
equals one on
K
tTp
,
(f
E (0, 1).
By
density. (2.5) implies
(2.7)
Vt/J
E X'oc(I:
T
),
VO<s<t~T,
t
!!
{Ut(t/J
- u)+(" + IDul,,-2
DuD[(t/J
- u)+("J} dxdT =
O.
BRN
Conversely.
if
t/J
E
C~
(I:T
).
we may write (2.7) for s < t such that supp{
t/J}
C
RN
x
(s,t).
By taking
(so
that p>2diam(supp{t/J}). we obtain (2.2).
We
con-
clude that the fonnulations
(2.2), (2.5) and (2.7)
are
equivalent.
LEMMA
2.2. Let
UES
satisfy
Then
Ut
-
div
IDul,,-2Du = 0
in
1>'(I:T).
PROOF:
In (2.5) take
t/J=Un
+ 1 E
X,oc:(I:T).
nEN.
We
obtain
V'1EC~(I:T)
! !{Ut'1 +
IDul,,-2
DuD'1}(u
n
-
U + l)+dxdT =
!!
IDuIP'1dxdT.
I:T
I:
T
n[n<u<n+1!
Since
IDul
E
Lfoc(I:
T
),
the right-hand side tends
to
zero as
n-
00.
The left-hand
side converges to
!!
{Ut'1
+ IDul,,-2DuD'1}
dxdT
=
O.
I:T
LEMMA
2.3. Let U E
S.
Then/or all k >
O.
Uk
is a distributional
super-solution
0/{1.1)
in
I:
T
.
PROOF:
Fix k>O and
Q,eE(O,
I),
and in (2.5) take
t/J
=
Uk
+
[(k
-
u)+
+
eJo
E
X,oc:(I:
T
)
to obtain
V'1EC~(I:T).
'1~0
!!{Ut'1 + IDul,,-2
DuD'1}(t/J
- u)+dxdT = !!IDuIP'1dXdT
I:T
I:Tn(k<UO/IJ
+ Q ! !IDUkl"[(k -
u)+
+ e)o-l'1 dxdT
~
O.
I:T
First we let e - 0 as Q E (0, 1) remains fixed. Since

(1/J
-
1£)+
-
(k
-
1£)+
we
deduce
j j{u,.,., +
IDuIP-2
DuD.,.,}(k
- u)+dxdr
~
0,
I:T
2.
Weak
solutions
339
Voe(o,
1).
Now
letting 0 - 0 gives for every non-negative.,., e O:'(I:
T
)
(2.8)
jj
{!
Uk""
+
IDUkIP-2DUk.D.,.,}
dxdr
~
O.
I:T
The next proposition pennits a large class
of
testing functions
in
(2.5). H
ko
>
0,
let
F(k
o
)
denote the set
of
all
the
Lipschitz-continuous functions I :
R+
- R
such that
l(k)=O, Vk>ko, and set
PROPOSITION
2.1.
LetueS.
Then
V/eF
andV.,.,eO:'(I:
T
),
j j{Ut/(u).,., +
IDuIP-2
Du·D(J(u).,.,)}dxdr =
O.
I:T
PROOF:
Assume
first that I e 0
2
(0,00). Write (2.5) for
1/J
=
k,
multiply it
by
-
f"
(k) and integrate in
dk
over
(0,
00).
By
interchanging the order of integration
with
the
aid of Fubini's theorem
we
obtain
00
jj
{u,.,.,j!"(k)(k - u)dk
I:T
U
+
IDuIP-'D,..D
[q
P"(k)(k -
U)dk]
}dzdT
=
o.
Since
00
j!"(k)(k
- u)dk =
1(1£),
U
the
assertion follows for I e 0
2
(0,
00).
The general case is proved
by
approxima-
tion.

340
XII.
Non-negative
solutions
in
E1.
The
case
I <p<2
3. Estimating
IDul
LEMMA
3.1. There exists a constant
'Y
= 'Y(N, p) such that
\fk>
0, \fp > 0,
\fO<s<t::5T,
\fu
E S
t
IllDUkl
P
dxdT
::5
'Y
kPlKpl
(k2-P +
t;
s)
.
BRN
PROOF:
Let ( be
the
standard cutoff function
in
K
2p
. Then
from
(2.7) with
1/J
= k
t t
IIIDUk/P(PdxdT:5 p II/DUk/P-1(P-l(k - u)+ID(ldxdT
BRN
SRN
t
+
~
II
!(k
- u)!(PdxdT
BRN
t
::5
p;
1 IIIDUkIP(PdXdT
BRN
t
+
pp-l
!
fik
-
u)~ID(IPdxdT
BRN
+
~
fik
- u)!(Pdx.
RNX{t}
For all
0<
s <
t::5
T
and
all p>O set
(3.1) Ms,t(p) = sup
fu(X,
T)
dx.
'Te(s,t)
Kp
LEMMA
3.2. Let
uES.
Then
\foE
(O,p - 1)
IDuP-~-Q
I E
Lroc(I:
T
),
and there exists a constant 'Y='Y(N,p) such that\fO<
s<t::5T
and/or
all p>O
PROOF:
Fix k > 0 and e E (0,1).
and
in
(2.8) take
'1
=
(P1/J-Q.
where (
is
the
standard cutoff function
in
K
2p
and

We
obtain
(3.3)
t
u>e
u
~e.
o
/JIDuIPu-Q-l(Px[e<u<kj
dxdr
BRN
t
3.
Estimating
IDul
341
~
P
//IDuIP-lu-Q(P-IID(lx[e<u<kjdXdT
sRN
t
+ p /
/IDu~IP-le-Q(P-IID(1
dxdr
sRN
By Young's inequality, the first integral on the right-hand side is majorised by
t
i /
/IDuI
P
u-Q-1(Px[e < u < kjdxdr
sRN
By
virtue
of
Lemma 3.1 the second integral tends to zero as e
-+
0 at the rate
of
e
P
-
1
-
Q
•
Combining these calculations we deduce
(3.4)
t
o
j/IDuIPu-Q-lx[e<u<kl
dxdr
BKp
~
O(eP-1-Q) +
"(_1
{
(sup
ju(x,
T)dx) l-Q
(2p)QN
oP
'TE(s,t)
K2p
+
(~)
(sup
ju(x,r)dx)P-I-Q
(2P)N(2-P+Q)}
pi'
'TE(s,t)
K2p
~
0:-
1
{[M
s
,t(2
P
)j1-Q
+
(t
;
s)
[MB,t(2
P
)jP-I-Q}
pN
+ O(e
P
-
1
-
Q
).

342
XII.
Non-negative
solutions
in
1:r.
The
case I <p<2
If
(t
~
8
)
~
[M
s
,t(2p)]2-
P
,
the quantity
in
braces on
the
rightmost side of (3.4)
is
majorised by
[Ms,t
(2p
W
-0<.
Otherwise
it
is
majorised by
In either case
t
(3.5)
JJIDuIPu-(O<+l)x.[e<u<k]dxdT
sKp
,,;
0(..-<0+1» +
:.
pH
{ M
•.•
(2p)
+ e ;
.)
,!;
r
o
,
and
the
lemma follows by letting first e-+O and
then
k-+oo.
Estimate (3.2) deteriorates
as
Q -+
o.
TIle next lemma gives some information
for the case
Q =
O.
LEMMA 3.3. Let
uES.
There exists 'Y='Y(N,p) such that
'liO<8<t~T,
'lip>
0, 'lin
~
1
t
J f
IDu¥
IPx.[n
<
u<
n +
1]
dxdT
sKp
(
1)
[
(t
-
8)
~l
~
'Yin
1 + n M
s
,t(2p) + 7 .
PROOF:
In
(2.8)
we
take
11
= (
1/J.
where (
is
the
standard cutoff function
in
K 2p
and
1/J=ln+
(~).
Here
We
get
t
u(n)
=
{n,
if
0 < u
~
n
u,
ifu
> n.
(3.6) JJIDuIPu-1x.[n<u<n+
l]dxdT
8
Kp
~
jJ!
un+lln+
(:~)1)
(PdxdT
SK2p
t
+
~
JJIDuIP-1ln+
(:~)1)
dxdT
=
I~l)
+
~
I~2).
SK2p
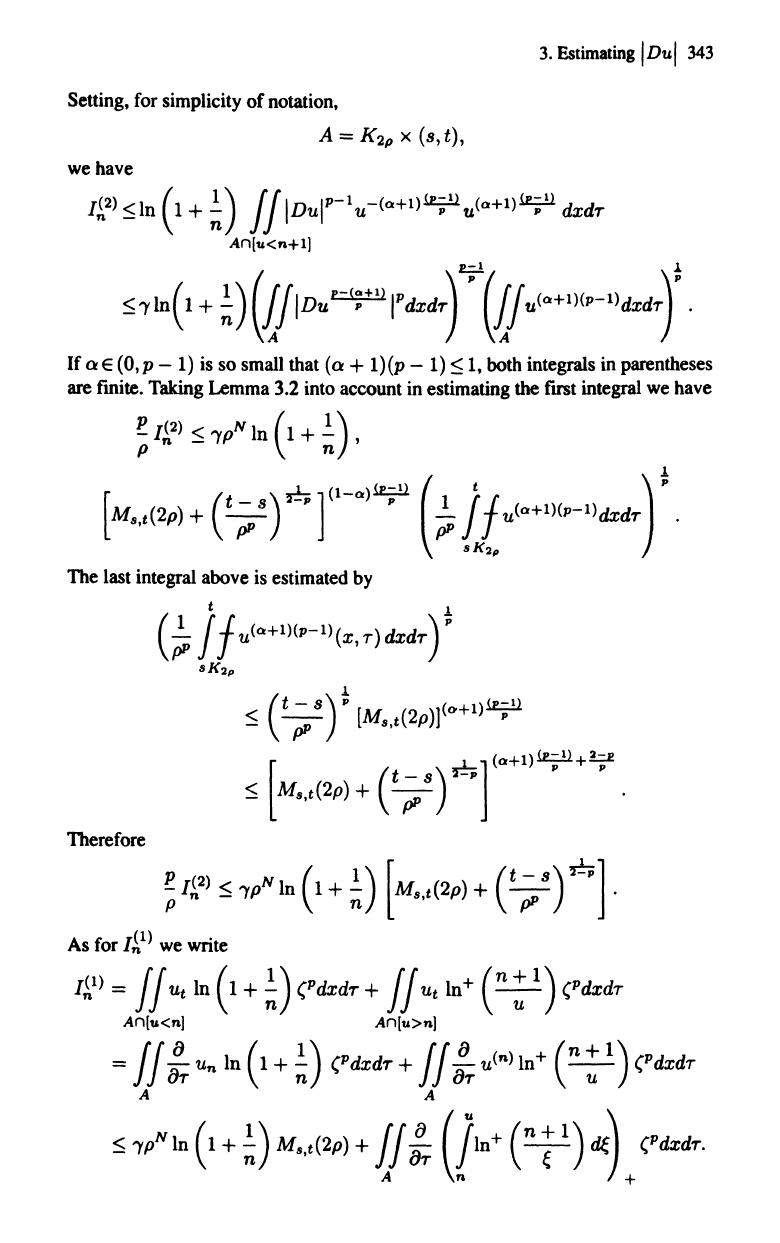
3.
Estimating
IDul 343
Setting, for simplicity
of
notation,
A = K
2p
x (s,t),
we
have
I~2)
~ln
(1
+~)
ff
IDuIP-1u-(Ot:+l)
(P;ll
u(Ot:+1)
(P;1)
dxdT
An[u<n+l]
.P=l
.1
$
~
In(
, +
;)
([.rID..
"¥'
I'
dxdT)
·
Vi
U<Q
+l)(p-l)
dxdT)'
If
Q E (0, P -
1)
is so small that (Q +
1)
(p -
1)
~
I, both integrals in parentheses
are
finite. Taking Lemma 3.2 into account in estimating
the
first integral
we
have
~
I~2)
~
1pN
In
(1
+
~)
,
.1
[Ms,t(2
P
)
+
(t
~
8
)
,.!;;
]
(l-Ot:)¥
(~
j /
U(Ot:+1HP_l)dxdT)
P
SK2p
The last integral above
is
estimated
by
t
.1
(~
f
/U(Ot:+lHP-l)
(x, T) dxdT ) P
SK2p
Therefore
~
t.')
$
~pNIn
(I+~)
[M
•••
(2
P) +
('
;;;:t].
As
for
I~l)
we
write
I~l)
=
ff
Ut
In
(1
+~)
(PdxdT +
ff
Ut
In+
(n:
1)
(PdxdT
An[u<n] An[u>n]
= ff!
Un
In
(1
+~)
(PdxdT +
ff
:T
u(n)
In+
(n:
1)
(Pdxdr
A A
~1pNln(1+~)Ms,t(2P)+
ff
:T
(jln+
(n;')d{\
("dxdT.
An)
+

344
XII.
Non-negative
solutions
in
~T'
The
case
1<p<2
COROLLARY
3.1. Let u E S and define
u{x,t)
(x,t)
->
z(x,t)
= /
(~lnl+E~)-;dx,
e
E E (O,p - 1).
Then
IDzl
E
Lfoc(ET)
and there exists "Y="Y(N,p) such that'v'O < s < t
~
T and
'v'p>O,
PROOF:
Divide both sides
of
the inequality
of
Lemma 3.3 by lnl+E n, and add
over all
n=2,3,
...
The estimate (3.7) deteriorates as
E-O.
The following corollary gives some
information in the case
E =
O.
COROLLARY
3.2. Let
uES.
Then
'v'O<s<t$T.
andforall
C>
1.
t
lim
ffIDuIP-I-l-
X[k<u<Ckjdxdr
=
O.
k
.....
oo}} U
nu
s Kp
PROOF:
Without loss
of
generality we may assume that k and
Ck
are
positive
integers. Divide both sides
of
the inequality
of
Lemma 3.3 by In n and add for
n=k,
k + 1,
...
,Ck.
This gives
t
//IDunUln
u)-lX[k<u<Ckj
dxdr
s Kp
[
(
t-
S)~l
~"Y{lnlnCk-Inlnk)
M
s
,t(2p)+
Ii'
(
InC)
[
(t
S)
~l
=
"YIn
1 +
Ink
M
s
•
t
(2p) +
Ii'
.
4. The weak Harnack inequality and initial traces
In the definition
of
local weak solutions
of
(2.1) in
ET,
no reference has been
made to initial data.
We
will show that each u E S has a unique non-negative
u-finite
Borel measure
J.I.
as the initial trace. The existence
of
such a trace will be
a consequence
of
the following weak Harnack-type estimate.

4. The weak Harnack inequality and initial traces 345
THEOREM
4.1.
Let
U E
S.
There exists
"I
= "I(N,p). such that
"10
< s < t
5,
T
andVp>O
!
j
(
t-S)~
(4.1) sup
u(x,
r)dx
5,
"I
u(x,
t)dx
+
"I
-.>.-
,
TE(s,t)
P
Kp
K2p
A =
N(p
-
2)
+
p.
The uniqueness
of
the initial trace
J.I.
relies on the next gradient estimates.
LEMMA
4.1.
Let
uES.
There exists a constant
"I="I(N,p)
such that
VO<s<t5,T,
"Ip>
0,
Vu
E (0,1),
"Iv>
0,
1 h
(t-S)~
(4.2)
p}}
IDulp-1dxdr
5,
"I
7-
B
Kp
:!iE..=..ll
+
"I
(t
-/)
* { sup
ju(x,
r)
dx}
P
P
S<T<t
K2p
Moreover
Ih'lt
j
(t-S)~
(4.3) -
IDulp-1dxdr
5,
"I
sup
u(x,
r)
dx
+
"I
-.>.-
.
p
S<T<t
P
S
Kp
K2p
PROOF:
The proof is the same as that
of
Propositions 4.1 and 4.2
of
Chap. VII.
The only difference is that instead
of
working with the solution u we work with
the truncations
Uk
and use the fact
that
these are supersolutions. In (2.8) we take
the testing functions
t/J
= (t
-r)*(uk
+
v)l-~
E X'oc(E
T
),
where
v>
0 is arbitrary.
We
proceed as in Chap. VII and then let k
~
00.
THEOREM
4.2. Every u E S has a unique Radon measure
J.I.
as
initial trace
at
t=O.
PROOF:
From Theorem 4.1 it follows that
V'1EC~(RN),
the net
{
jU(r)'1dx}
RN
TE(O.t)
is equibounded, with bound depending only upon
II
'1
II
oo,RN
• A subnet indexed
with {r'} converges to a Radon measure
1',
in the sense
of
the measures, i.e.,
