DiBenedetto E. Degenerate Parabolic Equations
Подождите немного. Документ загружается.


206
VB.
Harnack
estimates and extinction profile
for
singular equations
9.
Proof of the Harnack inequality
We
let u
be
a non-negative local weak solution
of
(1.1) in
nT
and let p be in the
range
(1.2).
Let
(xo,
to)
E
nT,
assume that
u(Xo,
to)
> 0 and consttuct the cylinder
Q4p(X
o
,
to)
==
{Ix -
xol
<
4p}
x {to -
[u(x
o
• t
o
)]2-" (4p)",
to
+
[u(xo,
t
o
)]2-" (4P)"}.
where
we
assume that p
is
so small that
Q4p(X
o
,
to)
c n
T
.
The change of variables
x-x
o
x~--,
p
Q+
==
B4
x [0,4"),
Denoting again with x and t the
new
variables, the rescaled function
is
a bounded non-negative weak solution
of
{
Vt
- div IDvl,,-2 Dv = 0
v(O,O)
=
1.
in
Q,
To
prove the theorem
it
suffices to determine constants c and
"Yo
in
(0, 1), depend-
ing only
upon
N and p such that
(9.1)
inf v(x,
c)
~
"Yo.
zEBl
9-(i).
Locating the sup
of
u in Q
For
TE
(0,1) consttuct the family
of
nested expanding cylinders
and
the numbers
M.,.
==
supv,
Q
..
Here 6 E (0,
1)
is
a small number to
be
chosen later and has the effect
of
rendering
'/lat' the boxes
Q.,..

9.
Proof of
the
Harnack
inequality
207
Remark
9.1. This construction
is
similar to that
in
the proof of Theorem
2.1
of
Chap.
VI. The cylinders
QT
however
are
'thin'
in the
t-dimension. Also the ex-
ponent of
(1
-
T)
in the definition of
NT
is
fixed and depends
on
the singularity
of the p.d.e.
For
T =
0,
we
have
Mo
=
No.
Moreover
as
T
/'
1
and
since
v E
L~(Q).
Therefore the equation
MT
=
NT
has
a largest root,
say
To,
which satisfies
Since
v
is
HOlder
continuous
in
Q,
it
achieves the value
MTo
at some point (x, f) E
QTo
and
(9.2)
sup
v(x,f)
$
2~(1-
To)-~.
Ix-zl< l-{A
LEMMA
9.1.
There
exist a positive number e that
can
be
determined a priori only
in
terms
of
N and p,
such
that
v(x
f'
>
~(I-'T.
)-~
,
OJ
- 2 0 ,
'v'lx
-
xl
< e(1 -
To).
Remark
9.2. The proof employs the estimates of Lemma
5.1
in
the
form
(5.3).
Therefore e "\.
0
as
p
/'
2.
PROOF
OF
LEMMA
9.1: Construct the
box
-
I-To
(x,
f) +
Q4R
==
{Ix -
xl
<
4R}
x
{f
-
4,
fl, where 4R =
-2-'
Apply to such a box the estimate (5.3) with the appropriate change of variables to
obtain
sup
v(x,
t) $ "Y(
!v(x,
f)dx)"/>"
+
"YR-~,
'v'f
- 1 $ t $
f.
Ix-zl<R
B2R
In
view of (9.2) and the definition of R
sup
v(x,
t) $
"Y1(1
-
To)-~,
Bi!.=;al
where
"Y1
=
"Y1
(N, p)
is
a constant that can
be
determined a priori only
in
terms of
N and p. Next consider the cylinder

208
VII.
Harnack
estimates
and
extinction profile
for
singular equations
By
virtue
of
such a construction we have
sup
v
~
"Yl(1-
TO)-~'
QRo
The 'vertical size'
of
Q Ro is larger than
Therefore Q Ro satisfies the space-time configuration
of
(8.1 )-(8.2). We conclude
that
'v'0
< p < Ro,
'v'lx
-
xl
<
p,
at the level f
v(x,f)
~
v (x, f) - "Y"Yl(l-
To)-~
(~J
Q
Since v (x, f) = (1 -
To)-~,
by taking p='TIRo.
'TIE
(0,1)
we find
vex, f)
~
(1
-
To)-~
(1
-
"Y"Yl'T1Q),
~
'v'lx
-
xl
~
'TIRo
==
'TI(8"Y1
p
)-1(1_
To)
and
the lemma follows by taking
'TI
so
small that enough (1 -
"Y"Y1
'TIQ)
= ! and
then choosing
9-(i;).
Time-expansion
o/positivity
The previous arguments are independent
of
the number 0. We will now de-
termine 0.
LEMMA
9.2.
There
exist small positive numbers
Co,
0 that
can
be determined a
priori only
in
terms
of
N and
p,
such
that
(9.3)
vex, t)
~
c
o
(1
-
To)-~,
'v'lx
-
xl
< e(1 -
To),
'v'o
~
t
~
20.
PROOF:
Considerthecomparisonfunction~
(x -
x;
t - f)
inthedomainV{k,~}
(x,
defined in
(7.1)-(7.2)
with the choices,
p =
e(l-
To).
The function
~
is a subsolution
of
(1.1) for a time interval
For
t = f by virtue
of
Lemma 9.1, v
~
~
(x
-
x;
0). Therefore
by
the comparison
principle
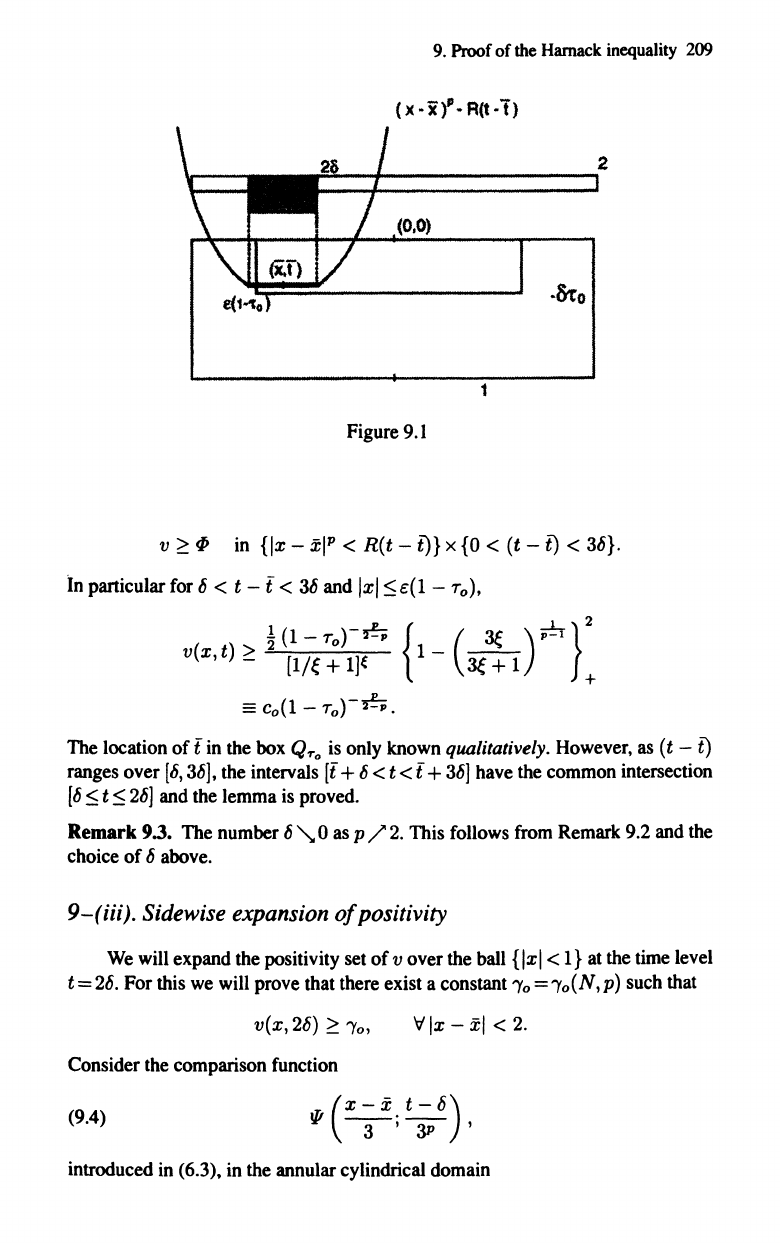
9.
Proof of
the
Harnack inequality
209
(x-i)"-R(t.l)
2
=---+----------------,
·&t
o
1
Figure
9.1
v
~
~
in
{Ix -
xl
P
<
R(t
-l)}
x
{O
< (t
-l)
< 36}.
In
particular
for
6 < t - t <
36
and
Ixl
:5
e(l
-
To),
~(l-TO)-~
{
(ae
);;!T}2
vex,
t)
~
[lie + 1]( 1 -
ae
+ 1 +
==
co(l -
To)-~.
The location of t
in
the
box
Q".o
is
only known qualitatively.
However,
as
(t
-l)
ranges over
[6,
36],
the intervals [t + 6 < t < t +
36]
have the common intersection
[6
:5
t
:5
26]
and the lemma
is
proved.
Remark
9.3. The number
6""
0
as
p /
2.
This follows
from
Remark
9.2
and
the
choice of 6
above.
9-(iii). Sidewise expansion
of
positivity
We
will expand the positivity set of v over the ball
{Ixl
<
I}
at
the
time
level
t=26. For this
we
will prove that there exist a constant
'Yo
='Yo(N,p)
such
that
vex,
26)
~
'Yo,
'v'lx
-
xl
<
2.
Consider the comparison function
(9.4)
(
X-x.~)
I/t
3'3P'
introduced
in
(6.3), in the annular cylindrical domain

210
VII.
Harnack
estimates and extinction profile
for
singular equations
{e(l-
To)
<
Ix
-
xl
< 3}x
{c5,2c5}.
The
number k
is
given
by
k =
co(l-
To)-r-;,
where Co
is
determined
in
Lemma 9.2. The
parameter
JJ
here can
be
chosen
by
imposing
Wechoose
i.e
.•
11'-1
e1'
u<---
r- -
2-1'
31'.
Co
{
I
11'-1
e
1'
}
JJ
= min
4;
~-1'
31'
'
and
pick
(J
according
to
the second of (6.4).
By
further restricting either
JJ
or
the
number
c5
of
Lemma
9.2
we
may
assume that
(J
=
c5.
The function
t[I
in
(9.4) vanishes
for
Ix
- xl=3 and
fort=c5.
Moreover for
Ix
-
xl
=e(l
-
To)
and
c5
<t~2c5.
(
x-x
t-6)
-'!.-
t[I
-3-'"""3P
~
co(l - To)-r-p
~
v(x, t),
by
Lemma 9.2. Therefore
by
the
comparison principle.
we
have for t =
26
and
Vlx-xl<2
9-(iv). Proof
of
Theorem
1.1
for p near 2
The
proof
is
very
similar to that of Theorem
2.1
of
Chap.
VI
for
p close to
2.
We
only indicate the main differences.
As
before. construct the
family
of expanding cylinders
Q.,.
==
{Ixl <
T}
x
{-T,
O}
and
the
numbers
M.,.
==
IIvlloo,Q.,.,
where
f3
is
a positive number
to
be
chosen. The definition of the numbers
N.,.
differs
from
that in
§9
since
(3
is
arbitrary. Let
To
E
[0,
1)
be
the largest
root
of the
equation
M.,.
=
N.,..
so that

10. Proof of Theorem 1.2
211
If
(x,
t) is a point in
QTo
where v achieves the value M
To
' we have
(9.5)
( )
p(
P I I -
To
- I -
To
-
vX,t
~2
I-T
o
)-;
x-xl<-2-;
t--
2
-<t<t.
Let
and consider the box
From the definitions
of
QT
and
Ro
we have Q 0 (x, t) c Q!:t;a, so that by (9.5),
IIvlloo,Qo(z,l)
~
2
P
(1
- To)-P
Therefore
Qo
(x,
t) satisfies the space-time configuration (8.1)-(8.2).
It
follows
that
\fIx -
xl
<
Ro,
Iv(x,
t) - v (x, t) I <
-y2
P
(1
- To)-P
(~)
Q
By
taking
p=eRo
and then e sufficiently small we have
LEMMA
9.1'. There exists a small positive number e E
(0,
I) that can be deter-
mined a priori only in terms
of
N,
p such that
I _
v(x f\ >
-(I
-
~)
P
,OJ
- 2
0,
P~
1
\fIx -
xl
<
e(1
-
To)
P + .
Remark
9.5. The constant e depends upon
f3
but it is 'stable' as p / 2 since no
use has been made
of
(5.3).
The proof can now be completed by expanding the positivity set
of
v with the
aid
of
the comparison function
g,.,p
introduced in §3-(i)
of
Chap. VI.
10. Proof
of
Theorem 1.2
Fix a point (x.,
t.)
E
aT
assume that
1.£
(x.,
t.)
> ° and for
R>
0, construct the
cylinder
Q8R
(x.,
t.)
==
{Ix
-
x.1
< 8R}
x
{t.
- c
[1.£
(x
..
, t
..
)]2-"
8R",
t.
+ c
[1.£
(x
..
, t.)]2-" 8R"} ,
where
c=c(N,p)
is
the
number appearing in Theorem 1.1, and R is any positive
number such that
Q8R
(x.,
t.)
is contained in the domain
of
definition
of
u.
We first establish an auxiliary proposition, then we will prove that it implies
the theorem.

212
VII.
Harnack
estimates
and
extinction profile
for
singular equations
PROPOSITION
10.1. There exists constants
C=C(N,p)
and,,=,,(N,p)
that
can be determined a priori only
in
terms
of
N and p, such that
(10.1)
C-
1
sup u(·,to)
~
u(xo,
to)
~
C inf
u(·,t
o
),
B"ReZ.)
B"Re
Z
.)
where
xo=x.
and
(10.2)
PROOF:
The change of variables
x-x.
x-
--
R '
t -
t.
t - 2
[u
(x.,
t.)]
-PRP
maps
QSR
(x.,
t.)
into Q = Bs x
(-8,8).
Denoting again
with
x
and
t the
new
variables.
the
rescaled function
v(x,
t)
=
(1
) u
(x.
+ Rx,
t.
[u
(x.,
t.)]2-
P
tRp)
u
x.,
t.
is a bounded non-negative solution of
{
Vt
- div IDvl
p
-
2
Dv
= 0 in Q.
v(O,O)
=
1,
We
first prove that there exist a quantitative constant C = C (N, p). such that
1 -
(10.3) C
~
v(x,
c)
~
C,
v
Ixl
<
1.
By
the Harnack inequality (1.3)
(10.4)
v(x,
c)
~
'Yo,
Vlx/
< 2,
for a quantitative constant
'Yo
=
'Yo
(N, p). This proves
the
estimate below
in
(10.3).
For the estimate above
we
require the following
lemma.
LEMMA
10.1. There exists a quantitative
constant"
E (0,1) depending only
upon N and p, such that
(10.5)
v(x,
-c)
~
2/'Yo,
Vlx/
<
2".
PROOF:
For x ranging over the ball
B4
consider
the
closed truncated 'paraboloid'
t + c
~
c [v(x. _c)]2-
p
Ix
-
xiI',
By
the Harnack estimate
-c
~
t
~
O.
(10.6) v(x,
-c)
~
2-
v
(x,
0),
Ix
-
xiI'
< [v(x,
_C)]p-2
,
'Yo

10.
Proof of Theorem
1.2
213
and in particular
v(O,
-c}
= lho. Since v is HOlder continuous, the set
{x
I
u(x,-c}
<2ho}
is non-empty and contains a ball about the origin. We claim that in particular it
contains the ball
B
2
f/'
where
(277}P
=
(~)
2-
p
•
If
not, there would exist some x E
B2f/
such that v(x,
-c}
=
2ho.
It follows that
the ball
Ix
-
xlP
< [v(x, _c}]p-2 =
(2'77}P
covers the origin, and (10.6) for x=O gives
2 1
- =
v(x,-c)
$
-.
~o ~o
The contradiction proves the lemma.
To prove the estimate above in (10.3), we combine the quantitative bound
(10.5) with Proposition 4.1. This gives
We return
to
the
original coordinates and write the estimate above in (10.3) as
u(x,t
o
}
$
Cu(x.,t.},
'v'lx
-
xol
<
77R,
XO
==
x
•.
Since,
by
Corollary 1.1, u
(x.,
t.)
$~u(xo,
to}
the left estimate in (10.1) is proved.
The estimate below in (10.3) reads
u(x,
to}
~
~ou
(x.,
t.)
,
On
the other hand the estimate above in (10.3) for x =
x.
gives u(x
o
,
to}
$
Cu
(x.,
t.).
Combining these last two estimates proves the bound above in (10.1)
and the proposition follows.
1D-(i).
Proof
of
Theorem
1.2
Fix (x
o
,
to)
E
fh
and p >
O.
Let
77
be
the
constant claimed by Lemma 10.1
and let
~
be
the
constant
of
the Harnack estimate (1.3). Set
~
r =
~
I'
p/T},
and construct the cylinder

214
VII.
Harnack
estimates
and
extinction profile
for
singular equations
QSr(X
o
,
to)
==
{Ix
-
xol
< 8r}
x {to - c
[u(xo,
t
o
)]2-" 8r", to + c
[u(xo,
t
o
)]2-" 8r" } .
Wthout
loss
of generality,
we
assume that
QSr(X
o
,
to)
c
nT.
First
fix
the time
level
and choose
R>
0
from
to -
t.
= c
[u
(x.,
t.)]2-"
R",
The
definitions of
t.
and
R give
c
[u(xo,
t
o
)]2-"
r"
= to -
t.
= c
[u
(x.,
t.)]2-" R".
By
Corollary 1.1, u
(x.,
t.)
~
')'u(xo, to). Therefore
2..=l
R
~
')'
p
rP
==
p/T/.
Applying Proposition
10.1
with such a choice of
the
point (x.,
t.)
and
radius R
proves the theorem.
11.
Bibliographical notes
Theorem
1.1
and
its
proof
is
taken
from
[44].
The
form
of Theorem
1.2
was
con-
ceived
by
Nash
[84],
who
believed it
to
be
true for solutions of the heat equation.
Moser
[83]
pointed out that (1.7)
is
not
dilation invariant
for
solutions of the heat
equation.
It
becomes scalar invariant
in
a specific
intrinsic
geometry.
The results
adapt
to
equations of porous
medium
- type
and
its
generalisations (see
[44
n.
In the
context of the plasma equations estimates of the rate
of
extinctions
were
derived
by
Berryman-Holland [13,14]. Proposition
3.1
is
due
to &nilan and Crandall
[9].
The estimates of
§§
4 and 5 are taken
from
[42].
The
subsolution
1/1
of
§6
appears
in
[44].
The
subsolution
~
of
§7
is
a modification of a subsolution introduced
in
[4].
It
is
natural
to
ask
whether
an
intrinsic Harnack estimate continues
to
hold
for
non-negative solutions of p.d.e. 's
with
full
quasilinear structure. This
is
the case if
p = 2 and it remains
an
open issue for degenerate (p>
2)
and singular
(1
< p <
2)
equations. A step
in
this direction
is
in
[29].
It
is
shown
that Theorem
1.1
holds
true for non-negative
weak
solutions
of
Vt
- (IDvl,,-2
aij
(x, t) u:J:;t, = 0,
,
where (x, t) --+
aij
(x, t)
are
only bounded and measurable
and
the
matrix (aij)
is
positive definite.

VIII
Degenerate
and
singular
parabolic
systems
1.
Introduction
We turn now to quasilinear systems whose principal part becomes either degener-
ate
or
singular at points where
IDul
= 0. To present a streamlined cross section
of
the theory. we refer to the model system
{
U::<Ut,U2,
...
,Um),
mEN,
(1.1)
Ui
E
C'oc
(0,
TjL~oc(n))nLP
(0,
Tj
w,!,:(n))
,
i=l,
2,
...
,m,
Ut
-
div
IDul
p
-
2
Du
= 0 in
nT'
The solutions are meant in the weak sense
t2 t2
(1.2) I
Uirpi(X,T)dXI
+ II
{-Uic,oi,t
+
IDuIP-2Dui·Dc,oi}
dxdT=O,
n
tl
tin
for all intervals [tl,
t2]
C (0,
T]
and all testing functions
cp
::
(cpt,
CP2,
••. ,
rpm)
satisfying
(1.3)
CPi
E W,!;;
(0,
T;
L2(n))
n
Lfoc
(0,
T;
wJ,p(n)),
i =
1,2,
...
, m.
For these we derive local sup-bounds
on
the modulus
of
the solution
lui
and its
space gradient
IDul
and establish the estimate
(1.4)
Ui,
zj
EC1:,c(nT),
i=I,2,
...
,m,
j=1,2,
...
,N,
