Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


CHAPTER 14
Fourier SeriesandApproximation
It is a natural problem to take a wave output and try to decompose it into its har-
monic parts. Engineers are able to do this with an oscilloscope. A real difficultly
occurs when we try to put the parts back together. Mathematically, this amounts
to summing up the series obtained from decomposing the original wave. In this
chapter, we examine this delicate question: Under what conditions does a Fourier
series converge? We begin with L
2
approximation and convergence, which has a
very clean answer. Nice applications of this include the isoperimetric inequality
and sums of various interesting series. Then we turn to the more subtle questions
of pointwise and uniform convergence. The idea of kernel functions, analogous
to the Poisson kernel from the previous chapter, provides an elegant method for
understanding these notions of convergence.
14.1. Least Squares Approximations
Approximation in the L
2
norm is important because it is readily computable.
Also, the partial sums of the Fourier series are well behaved in this norm, unlike
pointwise and uniform convergence, which we study later.
For the purposes of applications, we need to consider piecewise continuous
functions on [a, b], as given in Definition 5.2.4. Recall that there is a partition a =
x
0
< x
1
< ··· < x
N
= b of [a, b] so that f is continuous on each interval(x
i
, x
i+1
)
and one-sidedlimits existat each node. Note that a piecewisecontinuous function is
bounded by applying the Extreme Value Theorem on each interval [x
i
, x
i+1
]. Since
it is continuous on each of these intervals, it is also absolutely integrable. Hence
piecewise continuous 2π-periodic functions have Fourierseries. Theproduct of two
piecewise continuous functions is also piecewise continuous and thus is integrable.
So we can compute the L
2
inner product of two piecewise continuous functions by
extending the definition for continuous functions given in Example 7.4.4.
Given a piecewise continuous 2π-periodic function f with Fourier series
f ∼ A
0
+
∞
X
n=1
A
n
cosnθ + B
n
sinnθ,
463

464 Fourier Series and Approximation
let us denote the partial sums by S
N
f(θ) = A
0
+
P
N
n=1
A
n
cosnθ + B
n
sinnθ.
14.1.1. LEMMA. Every piecewisecontinuous 2π-periodic function f is the limit
in the L
2
(−π, π) norm of a sequence of trigonometric polynomials.
PROOF. Let x
0
= −π < x
1
< ··· < x
N
= π be a partition of f into continuous
segments. Fix n ≥ 1. Let M = kfk
∞
, and let
δ = min
n
1
32N(Mn)
2
,
x
i+1
− x
i
2
: 0 ≤ i < N
o
.
Define a continuous function g
n
on [−π, π] as follows. Let g
n
(x) = f (x) for
x ∈ [x
i
+ δ, x
i+1
−δ], 0 ≤ i < N. Also, set g
n
(−π) = g(π) = 0. Finally, make g
n
linear and continuous on each segment J
0
= [−π, −π + δ], J
i
= [x
i
− δ, x
i
+ δ],
1 ≤ i < N , and J
N
= [π − δ, π]. See Figure 14.1 for an example.
x
x
1
= −π
x
2
x
3
x
4
x
5
= π
y
1
2
−1
f
g
n
FIGURE 14.1. Piecewise continuous f with continuous approxi-
mation g
n
.
Observe that kg
n
k
∞
≤ kfk
∞
= M and therefore |f(x) − g
n
(x)| ≤ 2M .
Moreover, the two functions agree except on the intervals J
i
for 0 ≤ i ≤ N. The
total length of these intervals is 2N δ. Therefore, we can estimate
kf − g
n
k
2
2
≤
N
X
i=0
Z
J
i
(2M)
2
dx ≤ 8N M
2
δ ≤
1
4n
2
.
By Corollary 13.6.6, the 2π-periodic continuous function g
n
is the uniform
limit of trig polynomials. So there is a trig polynomial t
n
so that kg
n
−t
n
k
∞
<
1
2n
.
Then kg
n
− t
n
k
2
≤ kg
n
− t
n
k
∞
<
1
2n
as well.
kf − t
n
k
2
≤ kf − g
n
k
2
+ kg
n
− t
n
k
2
<
1
2n
+
1
2n
=
1
n
Hence f is an L
2
limit of trig polynomials. ¥
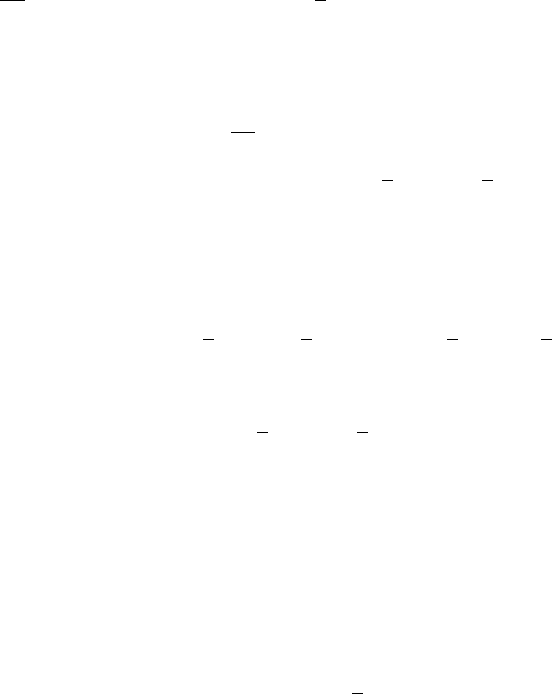
14.1 Least Squares Approximations 465
The main import of the following theorem is part (2), which states that the
partial sums S
N
f converge to f in the L
2
norm. Part (1) says that S
N
f is the
best L
2
approximant among all trig polynomials of degree N . Since S
N
f is a
trigonometric polynomial, it is continuous (and in fact C
∞
). But our result applies
to piecewise continuous functions. Since the uniform limit of continuous functions
remains continuous, this L
2
convergence is a weaker notion.
14.1.2. LEAST SQUARES THEOREM.
Suppose that f is a piecewise continuous, 2π-periodic function. Then
(1) If t(θ) is a trigonometric polynomial of degree N,
kf − tk
2
2
= kf − S
N
fk
2
2
+ kS
N
f − tk
2
2
.
(2) lim
N→∞
kf − S
N
fk
2
= 0.
(3)
1
2π
Z
π
−π
|f(θ)|
2
dθ = kfk
2
2
= A
2
0
+
1
2
∞
X
n=1
A
2
n
+ B
2
n
.
PROOF. The L
2
norm comes from an inner product, namely
hf, gi =
1
2π
Z
π
−π
f(θ)g(θ) dθ.
In Lemma 7.4.5, we have already proved that {1,
√
2cosnθ,
√
2sinnθ : n ≥ 1}
form an orthonormal set in C[−π, π], with this same inner product. Since that result
depends only on the inner product, it also shows that the same set of functions is
orthonormal in the larger inner product space of piecewise continuous, 2π-periodic
functions. Notice that
S
N
(f) = hf, 1i1 +
N
X
n=1
hf,
√
2cosnθi
√
2cosnθ + hf,
√
2sinnθi
√
2sinnθ.
Thus, by the Projection Theorem from Section 7.5, S
N
(f) is the best approximant
to f in the subspace spanned by {1,
√
2cosnθ,
√
2sinnθ : 1 ≤ n ≤ N}. Further,
the inequality (7.5.4) immediately establishes (1).
By Lemma 14.1.1, f is the limit of trigonometric polynomials in the L
2
norm.
Thus given ε > 0, choose a trig polynomial t with kf −tk
2
< ε. So it follows from
(1) that for n ≥ N = degt,
kf − S
n
fk
2
≤ kf − S
N
fk
2
≤ kf − tk
2
< ε.
Thus (2) holds. Finally,
kfk
2
2
= lim
N→∞
kS
N
fk
2
2
= A
2
0
+
1
2
∞
X
n=1
A
2
n
+ B
2
n
.
¥
466 Fourier Series and Approximation
14.1.3. EXAMPLE. Recall Example 13.3.2. It was shown that
|θ| ∼
π
2
−
4
π
∞
X
k=0
cos(2k + 1)θ
(2k + 1)
2
.
Compute the L
2
norm using our formula:
1
2π
Z
π
−π
|θ|
2
dθ =
³
π
2
´
2
−
1
2
³
4
π
´
2
∞
X
k=0
µ
1
(2k + 1)
2
¶
2
=
π
2
4
+
8
π
2
∞
X
k=0
1
(2k + 1)
4
.
The integral is easily found to be π
2
/3, from which we deduce that
∞
X
k=0
1
(2k + 1)
4
=
π
2
8
³
π
2
3
−
π
2
4
´
=
π
4
96
.
Hence
∞
X
k=1
1
k
4
=
∞
X
k=0
1
(2k + 1)
4
+
∞
X
k=1
1
(2k)
4
=
π
4
96
+
1
16
∞
X
k=1
1
k
4
.
Therefore,
∞
X
k=1
1
k
4
=
π
4
90
.
An immediate consequence of this theorem is that the sines and cosines span all
of C[−π, π]. Since they are orthogonal by Theorem 7.4.5, it follows that they are
an orthonormal basis. The last result of this section requires additional background
on Hilbert spaces, from Section 7.5. In Section 9.6, we showed that there is a
Hilbert space of functions, L
2
(−π, π), which is the completion of C[−π, π] in the
L
2
norm. Thanks to the abstract notion of integration developed there, we can
define, for each L
2
function, a Fourier series using the integration formulae given
in Definition 7.4.6.
If you have not studied Section 9.6, just consider elements of L
2
(−π, π) as
limits, under the L
2
norm, of sequences of continuous functions on [−π, π]. We
will not need the exact sense in which these limits are bona fide functions. To define
a Fourier series for the limit, use the limit of the Fourier series of the continuous
functions. The following theorem shows, among other things, that the limit of the
Fourier series exists.
14.1.4. COROLLARY. The functions {1,
√
2cosnθ,
√
2sinnθ : n ≥ 1} form
an orthonormal basis for L
2
(−π, π). The map sending a sequence a = (a
n
) in
`
2
(Z) to F a := f (θ) = a
0
+
∞
P
n=1
√
2a
n
cosnθ +
√
2a
−n
sinnθ is a unitary map.
That is, F maps `
2
(Z) one-to-one and onto L
2
(−π, π), and kF ak
2
= kak
2
for all
a ∈ `
2
(Z).

14.1 Least Squares Approximations 467
PROOF. We first define F just on the space `
0
of all sequences a with only finitely
many nonzero terms. Then F a is a trigonometric polynomial, and F maps `
0
onto
the set of all trig polynomials. Part (3) of Theorem 14.1.2 shows that kF ak
2
=
kak
2
for each a ∈ `
2
(Z). Thus F is one-to-one because kF a−F bk = ka−bk 6= 0
when a 6= b.
Theorem 7.5.8 shows that `
2
(Z) is complete and thus is a Hilbert space. Every
vector a is a limit of the sequence P
n
a =
n
P
k=−n
a
k
e
k
of vectors in `
0
. In particular,
this sequence is Cauchy. Therefore, for each ε > 0, there is an integer N so that
kP
n
a − P
m
ak
2
< ε for all n, m ≥ N. Consequently, the sequence of functions
F P
n
a = a
0
+
n
P
k=1
√
2a
k
coskθ +
√
2a
−k
sinkθ is also Cauchy because
kF P
n
a − F P
m
ak
2
= kP
n
a − P
m
ak
2
< ε for all n, m ≥ N.
So this sequence converges in the L
2
norm to an element f in L
2
(−π, π) (because
our definition of L
2
is the set of all such limits).
This function f has a Fourier series, and, for example,
A
k
= 2hf, cos kθi = lim
n→∞
2hF P
n
a,
1
√
2
F e
k
i =
√
2 lim
n→∞
hP
n
a, e
k
i =
√
2a
k
.
Hence f ∼ a
0
+
∞
P
k=1
√
2a
k
coskθ +
√
2a
−k
sinkθ. Moreover,
kfk
2
2
= lim
n→∞
kF P
n
ak
2
= lim
n→∞
kP
n
ak
2
=
∞
X
−∞
|a
n
|
2
= kak
2
2
This establishes a map F which maps `
2
(Z) into L
2
(−π, π) and preserves the
norm. If (Fa
n
) is Cauchy in L
2
(−π, π), then since ka
m
−a
n
k = kF a
m
−F a
n
k,
it follows that (a
n
) is Cauchy in `
2
(Z). If a is its limit, then F a = lim
n→∞
F a
n
belongs to the range. So the image space is complete. The range has been defined
as the completion of the trigonometric polynomials in the L
2
norm, and thus is a
subspace of L
2
(−π, π). Part (2) of Theorem 14.1.2 shows that the range of this map
contains every continuous function. Since the range is complete, it also contains
every L
2
limit of continuous functions. So the range is exactly all of L
2
(−π, π).
This completes the proof. ¥
14.1.5. REMARK. It is easy to deduce from Appendix 13.10 that the set of
complex exponentials {e
inθ
: n ∈ Z} also forms an orthonormal basis for the
Hilbert space L
2
c
(−π, π) of complex-valued L
2
functions. Indeed, because there
are no
√
2’s around, the formulae are cleaner. We define a map from the Hilbert
space `
2
c
(Z) of all square summable complex sequences c to the L
2
function with
complex Fourier series
∞
P
k=−∞
c
k
e
ikθ
. Again, this is a unitary map. In particular, if
468 Fourier Series and Approximation
f ∼
∞
P
k=−∞
c
k
e
ikθ
, then
kfk
2
2
=
1
2π
Z
π
−π
|f(θ)|
2
dθ =
∞
X
k=−∞
|c
k
|
2
.
The proofs are the same except that we need to use complex inner products.
Exercises for Section 14.1
A. Compute the Fourier series of f (θ) = θ
3
− π
2
θ for −π ≤ θ ≤ π. Hence evaluate the
sums
∞
P
n=0
(−1)
n
(2n + 1)
3
and
∞
P
n=1
1
n
6
.
B. Evaluate
∞
X
n=1
1
n
8
.
C. If f ∼ A
0
+
∞
P
n=1
A
n
cosnθ + B
n
sinnθ is a continuous 2π-periodic function, prove
that lim
n→∞
A
n
= lim
n→∞
B
n
= 0.
D. Show that {e
inθ
: n ∈ Z} forms an orthonormal basis for C[−π, π].
E. Use Exercise 13.3.I to find an orthonormal basis for C[0, π] in the given inner product.
F. (a) Compute the Fourier series of f(θ) = e
aθ
for −π ≤ θ ≤ π and a > 0.
(b) Evaluate kfk
2
in two ways, and use this to show that
1
a
2
+ 2
∞
X
n=1
1
a
2
+ n
2
=
π
a
µ
e
aπ
+ e
−aπ
e
aπ
− e
−aπ
¶
=
π
a
coth(aπ).
G. (a) Express Parseval’s Theorem in terms of the complex Fourier coefficients given in
Exercise 13.10.D.
(b) Let a ∈ R \ Z, and set f(θ) = e
iaθ
for θ ∈ [−π, π]. Evaluate kfk
2
2
in two ways to
deduce that
∞
P
n=−∞
1
(a − n)
2
=
π
2
sin
2
aπ
.
H. Recall the Chebychev polynomials T
n
(x) = cos(n cos
−1
x). Make a change of vari-
ables in Exercise E to show that the set {T
0
,
√
2T
n
: n ≥ 1} is an orthonormal basis
for C[−1, 1] for the inner product hf, gi
T
=
1
π
Z
1
−1
f(x)g(x)
dx
√
1 − x
2
.
I. Show that the map F of Corollary 14.1.4 preserves the inner product.
14.2. The Isoperimetric Problem
In this section, we provide an interesting and nontrivial application of least
squares approximation. The isoperimetric problem asks, What is the largest area
that can be surrounded by a continuous closed curve of a given length? The answer
is the circle, but a method for demonstrating this rigorously is not at all obvious.

14.2 The Isoperimetric Problem 469
Indeed, the Greeks were aware of the isoperimetric inequality. However, little
was done in the way of a rigorous proof until the work of Steiner in 1838. Steiner
gave at least five different arguments, but each one had a flaw. He could not es-
tablish the existence of a curve with the greatest area among all continuous curves
of fixed perimeter. This difficulty was not resolved for another 50 years. In 1901,
Hurwitz published the first strictly analytic proof. It is this proof that is essentially
given here.
For convenience, we shall fix the length of the curve C to be 2π. This is the
circumference of the circle of radius 1 and area π. We shall show that the circle
is the optimal choice subject to the mild hypothesis that C is piecewise C
1
. The
argument to remove this differentiability requirement is left to the Exercises.
Points on the curve C may be parametrized by the arc length s as (x(s), y(s))
for 0 ≤ s ≤ 2π. This is a closed curve, and thus x(2π) = x(0) and y(2π) = y(0).
Since the differential of arc length is
ds =
¡
x
0
(s)
2
+ y
0
(s)
2
¢
1/2
ds,
we have the condition
x
0
(s)
2
+ y
0
(s)
2
= 1.
The area A(C) is given by Green’s Theorem (see Exercise 6.4.I) as
A(C) =
Z
2π
0
x(s)y
0
(s) ds = 2πhx, y
0
i.
At this stage, we need a simple lemma for computing the Fourier series of a
derivative.
14.2.1. LEMMA. Suppose that f ∼ A
0
+
∞
P
n=1
A
n
cosnθ + B
n
sinnθ is a piece-
wise C
1
, 2π-periodic function. Then f
0
has the Fourier series
f
0
∼
∞
X
n=1
nB
n
cosnθ − nA
n
sinnθ.
PROOF. The Fourier coefficients of f
0
are obtained by integration by parts:
1
π
Z
π
−π
f
0
(t) cosnt dt =
1
π
f(t) cosnt
¯
¯
¯
¯
π
−π
+
1
π
Z
π
−π
f(t)n sinnt dt = nB
n
.
Similarly,
1
π
Z
π
−π
f
0
(t) sinnt dt =
1
π
f(t) sinnt
¯
¯
¯
¯
π
−π
−
1
π
Z
π
−π
f(t)n cosnt dt = −nA
n
.
And
1
2π
Z
π
−π
f
0
(t) dt =
1
2π
f(t)
¯
¯
¯
¯
π
−π
=
1
2π
¡
f(π) − f(−π)
¢
= 0. ¥
470 Fourier Series and Approximation
Since x and y are piecewise C
1
, they and their derivatives have Fourier series
x(s) ∼ A
0
+
∞
X
n=1
A
n
cosns + B
n
sinns
y(s) ∼ C
0
+
∞
X
n=1
C
n
cosns + D
n
sinns
x
0
(s) ∼
∞
X
n=1
−nA
n
sinns + nB
n
cosns
y
0
(s) ∼
∞
X
n=1
−nC
n
sinns + nD
n
cosns.
Let us integrate the condition x
0
(s)
2
+ y
0
(s)
2
= 1 to get
1 =
1
2π
Z
2π
0
x
0
(s)
2
+ y
0
(s)
2
ds
= kx
0
k
2
2
+ ky
0
k
2
2
=
1
2
∞
X
n=1
n
2
(A
2
n
+ B
2
n
+ C
2
n
+ D
2
n
).
The area formula yields
A(C) = 2πhx, y
0
i = π
∞
X
n=1
n(A
n
D
n
− B
n
C
n
).
Therefore,
π − A(C) =
π
2
∞
X
n=1
n
2
(A
2
n
+ B
2
n
+ C
2
n
+ D
2
n
) − π
∞
X
n=1
n(A
n
D
n
− B
n
C
n
)
=
π
2
∞
X
n=1
(n
2
− n)(A
2
n
+ B
2
n
+ C
2
n
+ D
2
n
)+
+
π
2
∞
X
n=1
n(A
2
n
− 2A
n
D
n
+ D
2
n
+ B
2
n
+ 2B
n
C
n
+ C
2
n
)
=
π
2
∞
X
n=1
(n
2
− n)(A
2
n
+ B
2
n
+ C
2
n
+ D
2
n
)+
+
π
2
∞
X
n=1
n(A
n
− D
n
)
2
+ n(B
n
+ C
n
)
2
.
The right-hand side of this expression is clearly a sum of squares and thus is
positive. The minimum value 0 is attained only if
D
1
= A
1
, C
1
= −B
1
, and A
n
= B
n
= C
n
= D
n
= 0 for n ≥ 2.

14.3 The Riemann–Lebesgue Lemma 471
Moreover, the arc length condition gives
1 =
1
2
(A
2
1
+ B
2
1
+ C
2
1
+ D
2
1
) = A
2
1
+ B
2
1
.
Therefore there is a real number θ such that A
1
= cosθ and B
1
= sinθ. Thus the
optimal solutions are
x(s) = A
0
+ cos θ cos s + sinθ sins = A
0
+ cos(s − θ)
y(s) = C
0
− sinθ cos s + cosθ sins = C
0
+ sin(s − θ).
Clearly, this is the parametrization of a unit circle centred at (A
0
, C
0
).
Finally, we should relate this proof to the historical issues discussed at the
beginning of this section. Hurwitz’s proof, as we just saw, results in an inequality
for all piecewise smooth curves in which the circle evidently attains the minimum.
It does not assume the existence of an extremal curve, avoiding this problematic
assumption of earlier proofs.
Exercises for Section 14.2
A. (a) Show that if f is an odd 2π-periodic C
1
function, then kfk
2
≤ kf
0
k
2
.
(b) Deduce that if f is a C
1
function on [a, b] such that f (a) = f (b) = 0, then
Z
b
a
|f(x)|
2
dx ≤
³
b − a
π
´
2
Z
b
a
|f
0
(x)|
2
dx.
HINT: Build an odd function g on [−π, π] by identifying [0, π] with [a, b].
B. Let f be a C
2
function that is 2π-periodic. Prove that kf
0
k
2
2
≤ kfk
2
kf
00
k
2
.
HINT: Use the Fourier series and Cauchy–Schwarz inequality.
C. (a) Consider the problem of surrounding the maximum area with a curve C of length 1
mile that begins and ends at points on a straight fence a mile long.
HINT: Reflect the curve in the fence.
(b) Consider the corresponding problem with a fence that makes a right angle and so
covers two sides of a large field.
D. Suppose that two rays make an angle α ∈ (0, π). Suppose that a curve of length 1
connects one ray to the other. Find the maximum area enclosed.
HINT: Consider the effect of the transformation in polar coordinates sending (r, θ) to
(r, πθ/α) on both area and arc length and apply Exercise C.
E. Use approximation by piecewise continuous functions to extend the solution of the
isoperimetric problem to arbitrary continuous curves.
14.3. The Riemann–Lebesgue Lemma
There are continuous functions with Fourier series that do not converge at every
point. Such an example was first found by du Bois Reymond in 1876. Further
examples have been found by Fej
´
er and by Lebesgue. Much more recently in
1966, Carleson solved a long-standing problem conjectured 50 years earlier by
Lusin. He showed that the Fourier series of a continuous function (and indeed any

472 Fourier Series and Approximation
L
2
function) converges for all θ except for a set of measure zero. These examples
and results are beyond the scope of this course. However, under mild regularity
conditions, we can establish convergence of the Fourier series.
We first show that if f is C
2
, then the convergence result is easy. With more
work, we will be able to handle functions that are only piecewise Lipschitz.
14.3.1. THEOREM. If f is a C
2
, 2π-periodic function, then its Fourier series
converges absolutely and uniformly to f.
PROOF. Let f ∼ A
0
+
∞
P
n=1
A
n
cosnθ + B
n
sinnθ. Since both f and f
0
are C
1
, by
Lemma 14.2.1 we have
f
0
∼
∞
X
n=1
nB
n
cosnθ − nA
n
sinnθ
and
f
00
∼
∞
X
n=1
−n
2
A
n
cosnθ − n
2
B
n
sinnθ.
By Lemma 13.3.1, the Fourier coefficients are bounded by 2kf
00
k
1
. Thus
|A
n
| ≤
2kf
00
k
1
n
2
and |B
n
| ≤
2kf
00
k
1
n
2
for n ≥ 1.
Hence as in Exercise 13.4.D, compute
kA
n
cosnθ + B
n
sinnθk
∞
≤
4kf
00
k
1
n
2
.
Since
∞
P
n=1
4kf
00
k
1
n
2
< ∞, the Weierstrass M-test shows that this Fourier series
converges absolutely and uniformly. Thus by Corollary 13.6.4, it follows that this
uniform limit equals f. ¥
14.3.2. EXAMPLE. Consider the function f(θ) = θ
3
− π
2
θ for −π ≤ θ ≤ π.
Notice that f (−π) = f(π) = 0, whence f is a continuous 2π-periodic function.
Moreover, f
0
(θ) = 3θ
2
− π
2
and again we have f
0
(−π) = f
0
(π) = 2π
2
. So f is
C
1
. Finally, f
00
(θ) = 6θ. Since f
00
(−π) 6= f
00
(π), this function is not C
2
.
