Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


14.4 Pointwise Convergence of Fourier Series 483
For the integral from δ to π, we have
Z
π
δ
¡
f(θ + t) − f (θ
+
)
¢
D
n
(t) dt =
Z
π
δ
f(θ + t) − f (θ
+
)
2π sint/2
sin(n +
1
2
)t dt
=
Z
π
δ
g(t) sin(n +
1
2
)t dt,
where
g(t) =
f(θ + t) − f (θ
+
)
2π sint/2
.
As g is piecewisecontinuous on [δ, π], we can apply the Riemann-Lebesgue Lemma
to this last integral. Thus, for all n sufficiently large,
¯
¯
¯
¯
Z
π
δ
¡
f(θ + t) − f (θ
+
)
¢
D
n
(t) dt
¯
¯
¯
¯
=
¯
¯
¯
¯
Z
π
δ
g(t) sin(n +
1
2
)t dt
¯
¯
¯
¯
<
ε
2
.
Combining these two estimates, we have
¯
¯
¯
¯
Z
π
0
¡
f(θ + t) − f (θ
+
)
¢
D
n
(t) dt
¯
¯
¯
¯
< ε
for all n sufficiently large, and thus the limit is zero. ¥
14.4.6. EXAMPLE. Let h be the following variant on the Heaviside step func-
tion:
h(x) =
(
−1 if −π < x < 0
1 if 0 ≤ x ≤ π.
Evidently, this function is piecewise C
1
. Let us compute its Fourier series. Since h
is odd, it has only sine terms.
B
n
=
1
π
Z
π
−π
h(x) sinnx dx
=
2
π
Z
π
0
sinnx dx
=
−2
nπ
cosnx
¯
¯
¯
¯
π
0
=
(
0 if n is even
4
nπ
if n is odd
Thus h ∼
∞
P
k=0
4
(2k + 1)π
sin(2k + 1)x.
The Dirichlet–Jordan Theorem tells us that this series converges to 1 for all
0 < x < π and to −1 for −π < x < 0. At the points of discontinuity, it converges
to the average 0. This latter fact is clear since sin kπ = 0 for all integers k. Let us
plug in a few points. For example, take x = π/2. Since sin(2k + 1)π/2 = (−1)
k
,
1 = h
¡
π
2
¢
=
∞
X
k=0
4
(2k + 1)π
(−1)
k
.

484 Fourier Series and Approximation
Therefore,
1 −
1
3
+
1
5
−
1
7
+ ··· =
π
4
.
Similarly, plugging in x = 1, we obtain
sin1 +
1
3
sin3 +
1
5
sin5 + ··· =
π
4
.
Both of these series converge exceedingly slowly. So they have no real computa-
tional value.
We will consider this function again in Example 14.6.5; see Figure 14.5 for a
graph of h and S
30
h.
Exercises for Section 14.4
A. (a) Compute the Fourier series for f(x) = x for −π ≤ x ≤ π.
(b) Find the sum of the series.
B. (a) Find the Fourier series for f(θ) = sinh(θ) for |θ| ≤ π.
(b) Find a constant c so that the Fourier series for f(θ) − cθ converges uniformly on
[−π, π].
C. Show that
∞
P
n=2
(−1)
n
2n
3
n
4
− 1
sinnx is the Fourier series of a piecewise C
1
function.
HINT: Use Exercise A to subtract a multiple of x to leave the uniformly convergent
Fourier series of a C
1
function.
D. Sum the Dirichlet kernel using complex exponentials.
E. Sum the series
∞
P
n=1
sinnθ
n
.
HINT: Exercise A and Exercise 13.3.D
F. (a) Show that the function h(x) = cos(x/2) for −π ≤ x ≤ π is continuous and
piecewise C
1
.
(b) Find the Fourier series for h. HINT: A
n
=
4(−1)
n−1
π(4n
2
− 1)
(c) Sum the series at the point x = 0 in two ways, and show that they yield the same
result.
HINT:
2
4n
2
− 1
=
1
2n − 1
−
1
2n + 1
G. Prove Dini’s Test: If f is a piecewise continuous 2π-periodic function such that
Z
π
0
1
t
¯
¯
¯
f(θ
0
+ t) + f(θ
0
− t)
2
− s
¯
¯
¯
dt < ∞,
then lim
n→∞
S
n
f(θ
0
) = s.
HINT: Study the proof of the Dirichlet–Jordan Theorem. Look for a place where this
integral condition may be used in lieu of the Lipshitz condition.
14.5 Gibbs’s Phenomenon 485
14.5. Gibbs’s Phenomenon
In this section, we show that pointwise convergence of Fourier series, which we
established in the previous section, is not good enough for many applications. In
particular, a sequence of functions can converge pointwise without “looking like”
their limit.
We have seen in Section 8.1 that pointwise convergence of functions allows
surprisingly bad behaviour. Such a phenomenon arises for the functions S
n
f near
any jump discontinuity of f. This was first discovered by an English mathemati-
cian, Wilbraham, in 1848. Around the turn of the century, it was rediscovered by
Michelson and then explained by Gibbs, a (now) famous American physicist, in a
letter to the journal Nature. For a discussion of this history, see [43]. Put simply,
whenever f has a jump discontinuity, the graphs of S
n
f overshoot f near the dis-
continuity and increasing n does not reduce the error, it only pushes the overshoot
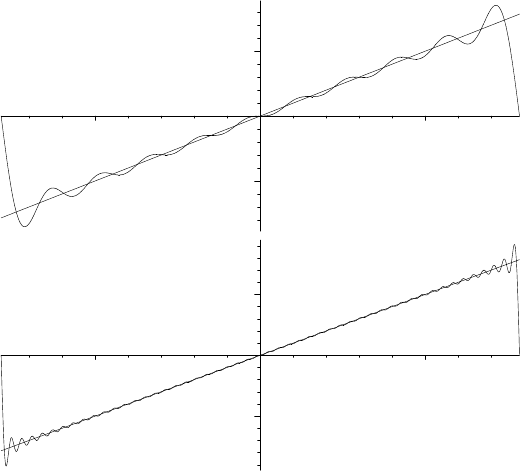
nearer to the discontinuity. See Figure 14.3, for example.
As an example, we demonstrate the phenomenon for the 2π-periodic function
given by
f(x) =
(
x if x ∈ (−π, π),
0 if x = ±π.
By the Dirichlet–Jordan Theorem (Theorem 14.4.5), lim
n→∞
S
n
f(x) = f(x), for
all x ∈ R. Nonetheless, S
n
f(x) always overshoots f(x) at some point near the
discontinuity by about 9% of the gap (which is 2π in this case).
–2
2
–2 2
–2
2
–2 2
FIGURE 14.3. The graphs of S
10
f and S
50
f, each plotted with f.
486 Fourier Series and Approximation
14.5.1. THEOREM. Let A =
2
π
Z
π
0
sin(x)
x
dx ≈ 1.178979744. For the func-
tion f defined previously, we have
lim
n→∞
S
n
f
¡
π(1 −
1
n
)
¢
= Aπ and lim
n→∞
S
n
f
¡
− π(1 −
1
n
)
¢
= −Aπ.
PROOF. Note that f is an odd function and hence has a sine series. An integration
by parts argument (see Exercise 14.4.A) shows that
f(x) ∼ 2
∞
X
k=1
(−1)
k+1
k
sinkx.
Thus,
S
n
f
¡
π(1 −
1
n
)
¢
= 2
n
X
k=1
(−1)
k+1
k
sin
³
kπ −
kπ
n
´
= 2
n
X
k=1
(−1)
k+1
k
³
sinkπ cos
kπ
n
− coskπ sin
kπ
n
´
and since sinkπ = 0 and cos kπ = (−1)
k
,
= 2
n
X
k=1
1
k
sin
kπ
n
=
π
n
n
X
k=1
2sin(kπ/n)
kπ/n
.
Remembering the formula for Riemann sums, we observe that this is the Riemann
sum for the integral of the function 2 sinx/x on the interval [0, π] using n+1 evenly
spaced points for the partition. Since lim
x→0
sinx/x = 1, this function is bounded and
continuous on [0, π]. Therefore, the Riemann sums converge to the integral. Thus,
we have
lim
n→∞
S
n
f
¡
π(1 −
1
n
)
¢
=
Z
π
0
2sinx
x
dx = πA
and, similarly,
lim
n→∞
S
n
f
¡
− π(1 −
1
n
)
¢
= −
Z
π
0
2sinx
x
dx = −πA.
It remains to estimate the integral A. The function (sinx)/x does not have a
closed form integral. However, we can get good mileage out of the Taylor series
for sinx because it converges so rapidly. Indeed, we obtain that
sinx
x
=
∞
X
k=0
(−1)
k
(2k + 1)!
x
2k

14.5 Gibbs’s Phenomenon 487
for all real x. Since this converges uniformly on [0, π], we may integrate term by
term by Theorem 8.3.1. Therefore,
A =
2
π
Z
π
0
sin(x)
x
dx =
2
π
Z
π
0
∞
X
k=0
(−1)
k
(2k + 1)!
x
2k
dx
=
∞
X
k=0
2
π
Z
π
0
(−1)
k
(2k + 1)!
x
2k
dx =
∞
X
k=0
2
π
(−1)
k
(2k + 1)!
π
2k+1
(2k + 1)
= 2
∞
X
k=0
(−1)
k
π
2k
(2k + 1)!(2k + 1)
= 2 −
π
2
9
+
π
4
300
−
π
6
17640
+ . . . .
Note that this is an alternating series in which the terms decrease monotonely
to 0. Therefore,
1.17357 ≈ 2 −
π
2
9
+
π
4
300
−
π
6
17640
< A
< 2 −
π
2
9
+
π
4
300
−
π
6
17640
+
π
8
1632960
≈ 1.17938.
This is enough for our purposes. However, using Maple, we found the integral to
be approximately 1.178979744. ¥
Gibbs’s phenomenon depends on the finite Fourier series being a best L
2
ap-
proximation; see [44] for a related example using using piecewise linear approx-
imations, much like Section 10.8 except that the L
2
norm replaces the uniform
norm.
Exercises for Section 14.5
A. (a) Suppose that h is a C
2
function on [−π, π] with h(π) = h(−π) but possibly
h
0
(π) 6= h
0
(−π). Show that S
n
h converges uniformly to h.
(b) Suppose that g is a C
2
function on [−π, π] but g(π) 6= g(−π). Subtract a multiple
of the function f used in this section from g to obtain a function h as in part (a).
(c) Hence show that g also exhibits Gibbs’s phenomenon.
B. (a) Follow through the proof of Gibbs’s phenomenon and show that
lim
n→∞
S
n
f
¡
π −
a
n
¢
=
Z
a
0
sinx
x
dx.
(b) Let t
n
=
Z
nπ
(n−1)π
sinx
x
dx. Show that t
n
alternates in sign, |t
n+1
| < |t
n
| and
lim
n→∞
t
n
= 0.
(c) Hence show that sup
a>0
¯
¯
¯
¯
Z
a
0
sinx
x
dx
¯
¯
¯
¯
=
Z
π
0
sinx
x
dx.
(d) Establish the existence of the improper Riemann integral
Z
∞
0
sinx
x
dx = lim
a→∞
Z
a
0
sinx
x
dx.

488 Fourier Series and Approximation
C. (a) Use the formula for D
n
as a sum of cosines to show that
Z
π−a
0
2πD
n
(x) dx = π − a + S
n
f(a),
where 0 < a < π and f(x) = x for −π ≤ x ≤ π.
(b) Hence show that
|S
n
f(a) − a| =
¯
¯
¯
¯
Z
(n+
1
2
)(π−a)
0
2sinx
(2n + 1) sin
x
2n+1
dx − π
¯
¯
¯
¯
.
(c) Use the Riemann–Lebesgue Lemma to show that
Z
(n+
1
2
)
π
2
0
2sin x
(2n + 1) sin
x
2n+1
−
2sinx
x
dx =
Z
π
2
0
g(x) sin(n +
1
2
)x dx
(for a certain continuous function g) tends to 0 as n goes to +∞.
(d) Use the Dirichlet–Jordan Theorem to deduce that
Z
∞
0
sinx
x
dx =
π
2
.
14.6. Ces
`
aro Summation of Fourier Series
Although it is natural to try to recombine the harmonics of a function f sim-
ply by adding the first number of terms, we have seen that such functions are not
good approximations to f in a number of ways. In this section we consider a new
sequence of approximations, built from the Fourier coefficients of f, that converge
uniformly to the function f for all continuous functions f . The results of this sec-
tion were found about 1900 by Fej
´
er, a Hungarian mathematician, at the age of 19.
In order to obtain this better behaviour, we replace the sequence of functions
S
n
f with their averages, known as Ces
`
aro means:
σ
n
f(x) =
1
n + 1
n
X
k=0
S
k
f(x).
This is defined whenever the Fourier coefficients of f are defined, which includes
all absolutely integrable functions. Our primary interest will be for continuous
functions. This new sequence of functions also has an associated kernel that is
much better behavedthan the Dirichlet kernel. Itshares manyof the good properties
of the Poisson kernel, and computing σ
n
f does not require an infinite sum. Indeed,
σ
n
f(x) =
1
n + 1
n
X
k=0
³
A
0
+
k
X
j=0
A
j
cosjx + B
j
sinjx
´
= A
0
+
n
X
j=0
³
1 −
j
n + 1
´³
A
j
cosjx + B
j
sinjx
´
.
Our first result is to turn this summation into an integral formula, using the
following sequence of functions.
14.6 Ces
`
aro Summation of Fourier Series 489
14.6.1. DEFINITION. The sequence of functions K
n
given by
K
n
(t) =
n + 1
2π
if t = 2mπ, m ∈ Z,
1
2π(n + 1)
µ
sin
n+1
2
t
sint/2
¶
2
if t 6= 2mπ,
for n = 1, 2, . . ., is called the Fej
´
er kernel.
14.6.2. THEOREM. If f : R → R is piecewise continuous and 2π-periodic,
then
σ
n
f(x) =
Z
π
−π
f(x + t)K
n
(t) dt.
PROOF. Using Theorem 14.4.2, we have
σ
n
f(x) =
1
n + 1
n
X
k=0
Z
π
−π
f(t + x)
sin(k +
1
2
)t
2π sint/2
dt
=
Z
π
−π
f(t + x)
1
2π(n + 1) sint/2
n
X
k=0
sin(k +
1
2
)t dt.
So all we need to establish is the trigonometric identity
n
X
k=0
sin(k +
1
2
)t sin t/2 =
µ
sin
n + 1
2
t
¶
2
as we can then divide through by sin
2
t/2 and substitute into the preceding integral
to obtain the equality in the statement of the theorem.
One method for computing this sum is to use complex exponentials to obtain a
geometric series as in Lemma 13.10.4. Here we will give a real variable argument
using trig identities. Applying the identity 2sinA sinB = cos(A−B)−cos(A+B)
with A = k +
1
2
and B = k/2 to the left-hand side of the identity gives
n
X
k=0
sin(k +
1
2
)t sin t/2 =
1
2
n
X
k=0
¡
coskt − cos(k + 1)t
¢
=
1
2
¡
1 − cos(n + 1)t
¢
=
³
sin
n + 1
2
t
´
2
,
where we have used the half-angle formula in the last step. ¥
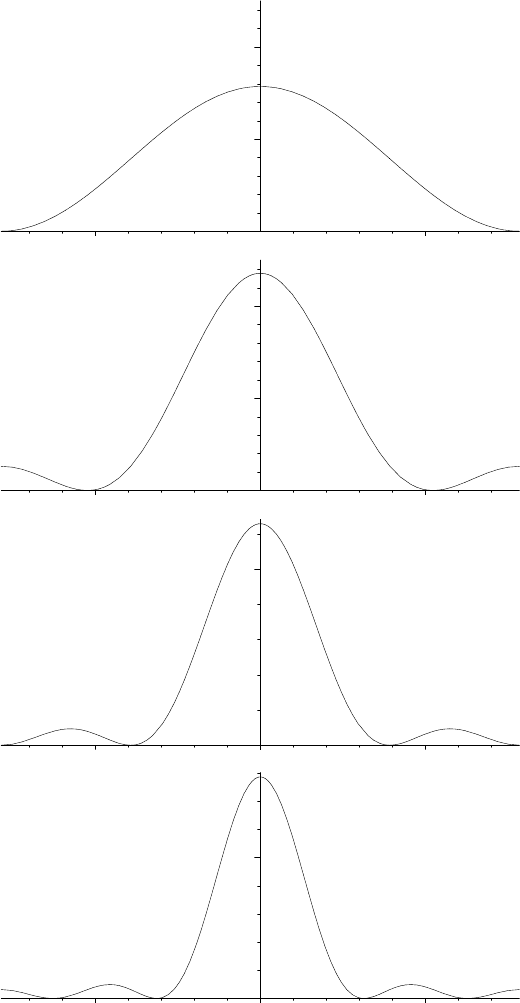
You should compare Figure 14.4 with the graphs of the Poisson and Dirichlet
kernels, Figures 13.2 and 14.2. The key difference between the kernels K
n
and
D
n
is that the K
n
are positive. Moreover, for t /∈ 2πZ, K
n
(t) → 0 as n goes to
infinity, unlike D
n
(t). However, K
n
(2πm) → ∞ as n goes to infinity, exactly like
D
n
. It is helpful to think of the K
n
as functions that become more and more like
spikes (i.e., large at zero and small elsewhere), as n goes to infinity. All of these
properties are shared with the Poisson kernel. This parallel allows us to obtain

490 Fourier Series and Approximation
similar convergence results. As before, we collect the important properties of the
K
n
in a proposition.
14.6.3. PROPERTIES OF THE FEJ
´
ER KERNEL. (1) For each n, K
n
is
a positive, continuous, 2π-periodic, even function.
(2)
Z
π
−π
K
n
(t) dt =
Z
π
−π
|K
n
(t)|dt = 1.
(3) For δ ∈ (0, π), lim
n→∞
µ
Z
−δ
−π
K
n
+
Z
π
δ
K
n
¶
= 0.
(4) Moreover, if δ ∈ (0, π), then K
n
converges uniformly to zero on
[−π, −δ] ∪ [δ, π].
PROOF. It is evident from the formula that K
n
is positive, even, 2π-periodic, and
continuous except possibly at multiples of 2π. Because of the periodicity, it suffices
to check continuity at 0. This is a simple consequence of the well-known limit
lim
t→0
sinat
t
= a. Hence
lim
t→0
K
n
(t) = lim
t→0
1
2π(n + 1)
Ã
sin
n+1
2
t
sint/2
!
2
= lim
t→0
1
2π(n + 1)
Ã
sin
n+1
2
t
t
!
2
µ
t
sint/2
¶
2
=
1
2π(n + 1)
µ
n + 1
2
¶
2
2
2
=
n + 1
2π
.
For (2), taking f = 1 in Theorem 14.6.2, we have
Z
π
−π
K
n
(t) dt = σ
n
f(0) = 1.
For (3), we could use the analogous fact for the D
n
and the averaging property.
However, (3) is an immediate consequence of (4). For (4), we let ε > 0 and observe
that |sint/2| ≥ sin δ/2 for t such that δ ≤ |t| ≤ π. Thus,
|K
n
(t)| ≤
1
2(n + 1)
1
|sinδ/2|
for all t ∈ [−π, −δ] ∪ [δ, π].
As δ is fixed, if we choose any N ≥ ε/(2 sin δ/2), then for all n ≥ N ,
|K
n
(t)| ≤ ε for all t ∈ [−π, −δ] ∪ [δ, π].
That is, K
n
converges uniformly to zero on [−π, −δ] ∪ [δ, π]. ¥
We can now prove the main result of this section.
14.6.4. FEJ
´
ER’S THEOREM.
If f is continuous and 2π-periodic, then σ
n
f converges uniformly to f.
14.6 Ces
`
aro Summation of Fourier Series 491
0
2
4
–2 2
0
2
4
–2 2
0
5
–2 2
5
–2 2
FIGURE 14.4. The graphs of K
1
, K
2
, K
3
, and K
4
.

492 Fourier Series and Approximation
PROOF. Conceptually, this proof is much like the proof of Poisson’s Theorem. We
write σ
n
f(x) as an integral from −π to π and then split the integral into two parts:
the interval [−δ, δ], and second, the rest, namely [−π, −δ] ∪[δ, π]. On the first part,
we control the integral using the fact that f is continuous; on the second, we control
the integral by using the fact that K
n
converges uniformly to zero.
Let M = kfk
∞
= max{|f(x)| : x ∈ [−π, π]} and let ε > 0. As f is con-
tinuous on the compact set [−π, π], it is uniformly continuous by Theorem 5.5.9.
Hence there is some δ > 0 so that
|f(x) − f(y)| <
ε
2
whenever |x − y| < δ.
With this δ fixed, we apply Theorem 14.6.3 (4), to conclude that there is an integer
N so that
K
n
(x) <
ε
8πM
for all x ∈ [−π, −δ] ∪ [δ, π] and n ≥ N.
Using Theorem 14.6.2 and Theorem 14.6.3 (2), we have
|σ
n
f(x) − f(x)| =
¯
¯
¯
¯
Z
π
−π
f(x + t)K
n
(t) dt − f(x)
Z
π
−π
K
n
(t) dt
¯
¯
¯
¯
=
¯
¯
¯
¯
Z
π
−π
¡
f(x + t) − f (x)
¢
K
n
(t) dt
¯
¯
¯
¯
≤
Z
π
−π
|f(x + t) − f (x)|K
n
(t) dt.
Now, we split this integral into two parts, as promised above. Let I
1
= [−δ, δ] and
I
2
= [−π, −δ] ∪ [δ, π]. If t ∈ I
1
, then |f(x + t) − f (x)| < ε/2, and so
Z
I
1
|f(x + t) − f (x)|K
n
(t) dt ≤
Z
I
1
ε
2
K
n
(t) dt
≤
ε
2
Z
π
−π
K
n
(t) dt =
ε
2
.
If t ∈ I
2
, then |K
n
(t)| ≤ ε/(8πM) and so
Z
I
2
|f(x + t) − f (x)|K
n
(t) dt ≤
Z
I
2
2MK
n
(t) dt
≤ 2M
Z
I
2
ε
8πM
dt <
ε
4π
Z
π
−π
dt =
ε
2
.
Adding these two results, we have
|σ
n
f(x) − f(x)| ≤
Z
π
−π
|f(x + t) − f (x)|K
n
(t) dt ≤
ε
2
+
ε
2
= ε
for all x ∈ [−π, π] and all n ≥ N. Thus, by the definition of uniform convergence,
σ
n
f converges uniformly to f. ¥
