Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

CHAPTER 15

Wavelets

15.1. Introduction

In this chapter we develop an important variation on Fourier series, replacing

the sine and cosine functions with new families of functions, called wavelets. The

strategy is to construct wavelets so that they have some of the good properties of

trig functions but avoid the failings of Fourier series that we have seen in previ-

ous chapters. With such functions, we can develop new versions of Fourier series

methods that will work well for problems where traditional Fourier series work

poorly.

What are the good properties of trig functions? First and foremost, we have an

orthogonal basis in L

, namely the set of functions sin(nx) and cos(nx) as n runs

over N

. This leads to the idea of breaking up a wave into its harmonic constituents,

as the sine and cosine functions appear in the solution of the wave equation. We

want to retain some version of this orthogonality.

Fix a positive integer n and consider the span of {sin(nx), cos(nx)}, call it

. If f(t) is in the subspace A

then so is the translated function f(t − x) and,

for a positive integer k, the dilated function f(kt) is in A

(see Exercise 15.1.A).

That is, translation leaves each subspace A

invariant and dilation by k carries

to A

for each n. Moreover, these orthogonal subspaces together span all of

[−π, π]. There is a similar decomposition for wavelets, called a multiresolution,

and it is central to the study of wavelets.

What are the problems with Fourier series that we would like to ﬁx? Fourier

coefﬁcients, andhence the Fourier series approximation, depend on all valuesof the

function. For example, if you change a function f a small amount on the interval

[0, 0.01], it is possible that every Fourier coefﬁcient changes. This will then have

an effect on the partial sums S

f(θ) for all values of θ. Although these changes

may be small, there are many subtleties in analyzing Fourier series approximations,

as we have seen.

Further, for a badly behaved function, such as a nondifferentiable or discon-

tinuous one, the coefﬁcients decrease slowly. Exercises 13.4.F and 13.4.C show

that the Fourier coefﬁcients of a function go rapidly to 0 only when the functions

has several continuous derivatives. Thus, we may need many terms to get a close

513

514 Wavelets

approximation, even at a point relatively far away from the discontinuity, as in Ex-

ample 14.4.6.

The partial sums S

f(θ) do not always converge to f(θ) when f is merely con-

tinuous. Thanks to Gibbs’s phenomenon, S

f(θ) will always exhibit bad behaviour

near discontinuities, no matter how large n is. While we can get better approxima-

tions by using σ

f(θ) instead of S

f(θ), this will not resolve such problems as

slowly decreasing Fourier coefﬁcients.

This suggests looking for a series expansion with better local properties, mean-

ing that coefﬁcients reﬂect the local behaviour of the function and a small change

on one interval affects only a few of the series coefﬁcients and leaves unchanged

the partial sums elsewhere in the domain. It may seem unlikely that there are useful

wavelet bases with this local approximation property that still have nice behaviour

under translation and dilation. However, they do exist, and they were developed in

the 1980s. The discovery has provoked a vast literature of both theoretical and prac-

tical importance. No one family of wavelets is ideal for all problems, but we can

develop different wavelets to solve speciﬁc problems. Developing such wavelets is

an important practical problem.

In this chapter, we will illustrate some of the general features of wavelets. The

basic example is the Haar wavelet, a rather simple case that is not the best for

applications but illuminates the general theory. We construct one of the most used

wavelets, the Daubechies wavelet, although we don’t prove that it is continuous.

This requires tools we don’thave; most notably, the Fouriertransform. We establish

the existence of another continuous wavelet, the Franklin wavelet, but this requires

considerable work. Our focus is the use of real analysis in the foundational theory.

We leave the development of efﬁcient computational strategies to more specialized

treatments, such as those in the bibliography.

Most of the literature deals with bases for functions on the whole real line rather

than for periodic functions, so we will work in this context. This means that we will

be looking for special orthonormal bases for L

(R), the Hilbert space of all square

integrable functions on R with the norm

kfk

+∞

−∞

|f(x)|

dx.

As in Section 9.6, we deﬁne L

(R) as the completion of C

(R), the continuous

functions of compact support on R, in the L

norm.

15.1.1. DEFINITION. A wavelet is a function ψ ∈ L

(R) such that the set

(x) = 2

k/2

ψ(2

x − j) : j, k ∈ Z

forms an orthonormal basis for L

(R). Sometimes ψ is called the mother wavelet.

This is more precisely called a dyadic wavelet to stress that dilations are taken

to be powers of 2. This is a common choice but is not the most general one. No-

tice that the wavelet basis has two parameters, whereas the Fourier basis for L

(T)

has only one, given by dilation alone. From the complex point of view, sines and

15.2 The Haar Wavelet 515

cosines are written in terms of the exponential function ψ(θ) = e

iθ

, and the func-

tions ψ(kθ) = e

ikθ

for k ∈ Z form an orthonormal basis for L

(−π, π). A singly

generated family of this form cannot have the local behaviour we are seeking.

Exercises for Section 15.1

A. (a) Given a Fourier series f (θ) ∼ A

∞

n=1

cosnθ + B

sinnθ, if f(kθ) ∼

∞

i=1

cosiθ + D

siniθ, ﬁnd the formula for C

and D

in terms of the A

the B

, and k.

(b) Similarly, if f(θ − x) ∼ A

∞

i=1

cosiθ + D

siniθ, ﬁnd the formula for C

and D

in terms of the A

, the B

, and x.

B. Show that if ψ is a function in L

(R) such that {ψ

: j ∈ Z} is an orthonormal set,

then {ψ

: j ∈ Z} is an orthonormal set for each k ∈ Z.

C. A map U from a Hilbert space H to itself is unitary if kUxk = kxk for all vectors

x ∈ H and UH = H. Deﬁne linear maps on L

(R) by T f(x) = f(x − 1) and

Df(x) =

√

2f(2x). Show that these maps are unitary.

D. Let ψ be a wavelet, and let T and D be the unitary maps deﬁned in Exercise C. What

is the relationship between the subspaces spanned by {T

Dψ : n ∈Z} and {DT

ψ :

n∈Z}?

E. Let ψ be a function in L

(R) such that {ψ

: j ∈ Z} is an orthonormal set. Let

the characteristic function of the set {x ∈ R : x − [x] <

}, where [x] is the greatest

integer n ≤ x. Deﬁne ϕ(x) =

(x)ψ(−x −

) − (1 −

(x))ψ(

− x).

(a) Show that ϕ is orthogonal to ψ

for all j ∈ Z.

(b) Hence deduce that there is no function ψ in L

(R) such that the set of translates

{ψ

: j ∈ Z} is an orthonormal basis for L

(R).

, ϕ

: j ∈ Z} is an orthonormal set.

F. For t ∈ R, deﬁne T

f(x) = f(x − t) for f ∈ L

(R). Show that if lim

n→∞

= t, then

lim

n→∞

f = T

f for every f ∈ L

(R).

HINT: If f is continuous with compact support, use the fact that it is uniformly con-

tinuous. Next, approximate an arbitrary f.

15.2. The Haar Wavelet

To get started, we describe the Haar system for L

(0, 1). This will then lead

to a wavelet basis for L

(R). For a < b, let

[a,b)

denote the characteristic function

of [a, b). Set ϕ =

[0,1)

and ψ =

[0,.5)

−

[.5,1)

. Then deﬁne

(x) = 2

k/2

ψ(2

x − j) for all k, j ∈ Z.

We only use those functions that are supported on [0, 1), namely 0 ≤ j < 2

for

each k ≥ 0. The others will be used later. The Haar system is the family

ϕ, ψ

: k ≥ 0 and 0 ≤ j < 2

See Figure 15.1 for examples of elements of the Haar system.

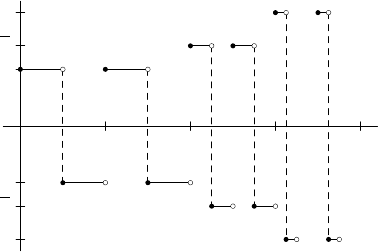
516 Wavelets

1 2 3 4

−1

−

√

−2

√

0,0

0,1

1,4

1,5

2,12

2,14

FIGURE 15.1. Some elements of the Haar system.

15.2.1. LEMMA. The Haar system is orthonormal.

PROOF. It is straightforward to check that each of these functions has norm 1.

Now ψ

and ψ

for j 6= j

have disjoint supports and thus are orthogonal. More

generally, if k < k

, then ϕ and ψ

are constant on the support of ψ

. Since

(x) dx = 0 for all j and k, it now follows that these functions are pairwise

orthogonal. ¥

We may consider the inner product expansion with respect to this orthonormal

set. It is natural to sum all terms of the same order at the same time to obtain a

series approximants. Therefore, we deﬁne

f(x) = hf, ϕiϕ(x) +

n−1

k=0

−1

j=0

hf, ψ

iψ

(x).

The Haar coefﬁcients are the inner products hf, ψ

i used in this expansion.

While we have some work yet to see that this orthogonal system spans the

whole space, we can see that it has some nice properties. The local character is

seen by the fact that these functions have smaller and smaller supports. If f and

g agree except on the interval [3/8, 1/2), then the Haar coefﬁcients are the same

for about “7/8ths of the terms” in the sense that hf, ψ

i = hg, ψ

i if k ≥ 3 and

j/2

6∈ [3/8, 1/2).

This is the kind of local property we are seeking. The functions ψ

also have

the translation and dilation properties we are want. However, we will have to elim-

inate ϕ somehow. We shall see that ϕ is not needed for a basis of L

(R) when we

add in dilations of ψ by negative powers of 2. On the other hand, ϕ reappears in a

central role in the next section as the scaling function.

We need a more explicit description of H

f. By a dyadic interval of length

−n

, we mean one of the form [j2

−n

, (j + 1)2

−n

) for some integer j.

15.2 The Haar Wavelet 517

15.2.2. LEMMA. Let f ∈ L

(0, 1). Then H

f is the unique function that is

constant on each dyadic interval of length 2

−n

in [0, 1] and satisﬁes

f(x) = 2

(j+1)2

−n

f(t) dt = 2

(j+1)2

−n

f(t) dtx

for x ∈ [j2

−n

, (j + 1)2

−n

), 0 ≤ j < 2

. Moreover, kH

≤ kfk

PROOF. It is easy to see that {ϕ, ψ

} span the functions that are constant on

[0, 1/2) and on [1/2, 1). By induction, it follows easily that

:= span{ϕ, ψ

: 0 ≤ k ≤ n − 1 and 0 ≤ j < 2

}

is the subspace of all functions that are constant on each of the dyadic intervals

[j2

−n

, (j + 1)2

−n

) for 0 ≤ j < 2

. Notice that M

is also spanned by the charac-

teristic functions

n,j

[j2

−n

,(j+1)2

−n

)

for 0 ≤ j < 2

Now H

f is contained in the preceding span and therefore is constant on

these dyadic intervals. Thus H

f is the unique function of this form that satis-

ﬁes hH

f, ϕi = hf, ϕi and hH

f, ψ

i = hf, ψ

i for 0 ≤ k ≤ n − 1 and

0 ≤ j < 2

. But this basis for M

may be replaced by the basis of characteristic

functions. Since k

n,j

= 2

−n

, H

f is the unique function in M

such that

f(x) = 2

n,j

i = 2

hf,

n,j

for all x ∈ [j2

−n

, (j + 1)2

−n

) and 0 ≤ j < 2

, which is what we wanted.

The map H

is the orthogonal projection of L

(0, 1) onto M

. The inequal-

ity kH

≤ kf k

follows from the Projection Theorem (Theorem 7.5.2). An

elementary direct argument is outlined in Exercise 15.2.C. ¥

We can now prove that the Haar system is actually a basis. Moreover, we show

that it does an excellent job of uniform approximation for continuous functions as

well, even though the basis functions are not themselves continuous. In this respect,

we obtain superior convergence to the convergence of Fourier series.

15.2.3. THEOREM. Let f ∈ L

(0, 1). Then H

f converges to f in the L

norm. Consequently, the Haar system is an orthonormal basis for L

(0, 1). More-

over, if f is continuous on [0, 1], then H

f converges uniformly to f.

PROOF. We prove the last statement ﬁrst. By Theorem 5.5.9, f is uniformly con-

tinuous on [0, 1]. Recall from Deﬁnition 10.4.2 that the modulus of continuity is

ω(f; δ) = sup{|f(x) − f(y)| : |x −y| ≤ δ}. The remarks there also show that the

uniform continuity of f implies that lim

n→∞

ω(f; 2

−n

) = 0.

518 Wavelets

For x ∈ [j2

−n

, (j + 1)2

−n

), compute

f(x) − f(x)| =

(j+1)2

−n

f(t) dt − 2

(j+1)2

−n

f(x) dt

≤ 2

(j+1)2

−n

|f(t) − f(x)|dt

≤ 2

(j+1)2

−n

ω(f; 2

−n

) dt = ω(f;2

−n

Hence kH

f − fk

∞

≤ ω(f;2

−n

) tends to 0. Therefore, H

f converges to f

uniformly on [0, 1].

Now

f − fk

≤

f − fk

∞

1/2

= kH

f − fk

∞

So we obtain convergence in the L

(0, 1) norm as well.

Next suppose that f is an arbitrary L

function, and let ε > 0 be given. As

f is the L

limit of a sequence of continuous functions, we may ﬁnd a continuous

function g with kf − gk

< ε. Now choose n so large that kH

g − gk

< ε. Then

f − fk

≤ kH

f − H

gk + kH

g − gk

+ kg − fk

≤ kH

(f − g)k

+ ε + ε

≤ kf − gk

+ 2ε < 3ε.

So H

f converges to f in L

Finally, since the orthogonal expansion of f in the Haar system actually sums

to f in the L

norm, we deduce that this orthonormal set spans all of L

(0, 1) and

thus is a basis. ¥

15.2.4. DEFINITION. The Haar wavelet is the function ψ =

[0,.5)

−

[.5,1)

The Haar wavelet basis is the family {ψ

: k, j ∈ Z}.

Lemma 15.2.1 can be easily modiﬁed to show that the Haar wavelet basis is

orthonormal. It remains to verify that it spans L

(R).

15.2.5. THEOREM. The Haar wavelet basis spans all of L

(R).

PROOF. It is enough to show that any continuous function of bounded support

is spanned by the Haar wavelet basis. Each such function is the ﬁnite sum of

(piecewise) continuous functions supported on an interval [m, m + 1). But our

basis is invariant under integer translations. So it is enough to show that a function

on [0, 1) is spanned by the Haar wavelet basis. But Theorem 15.2.3 shows that the

functions ψ

supported on [0, 1) together with ϕ span L

(0, 1). Consequently, it

is enough to approximate ϕ alone.

15.2 The Haar Wavelet 519

Consider the functions ψ

−k,0

= 2

−k/2

[0,2

k−1

)

−

k−1

)

for k ≥ 1. An easy

computation shows that

k=1

−k/2

−k,0

= (1 − 2

−N

)

[0,1)

− 2

−N

[1,2

)

Thus kϕ−h

= k2

−N

[0,2

)

= 2

−N/2

. Hence ϕ is in the span of the wavelet

basis. Therefore, the Haar wavelet basis spans all of L

(R). ¥

Exercises for Section 15.2

A. Let f(x) =

−1

k=0

n,j

[j2

−n

,(j+1)2

−n

)

and let s

= (s

n,0

, . . . , s

n,2

−1

(a) Deﬁne a

= (a

k,0

, . . . , a

k,2

−1

) and s

= (s

k,0

, . . . , s

k,2

−1

) by

k,j

k+1,2j

− s

k+1,2j+1

√

and s

k,j

k+1,2j

+ s

k+1,2j+1

√

for

0 ≤ k < n and 0 ≤ j < 2

. Show that f = s

0,0

ϕ +

n−1

k=1

−1

j=0

k,j

(b) Explain how to reverse this process and obtain s

from the wavelet expansion of f.

B. Let f be a continuous function with compact support [0, 1]. Fix n ≥ 1, and deﬁne

= f(j/2

) for 0 ≤ j < 2

. Show that

f −

−1

k=0

[j2

−n

,(j+1)2

−n

)

∞

≤ ω(f;2

−n

C. Prove that kH

≤ kfk

HINT: Show that it is enough to prove that

a+2

−k

f(x) dx

≤ 2

−k

a+2

−k

|f(x)|

dx.

Verify this using the Cauchy–Schwarz inequality.

D. Show that {ψ

: k > −N, −2

k+N

≤ j < 2

k+N

} together with the functions

−N,0

= 2

−N/2

ϕ(2

−N

x) and ϕ

−N,−1

= 2

−N/2

ϕ(2

−N

x + 1) forms an orthonormal

basis for L

(−2

, 2

E. Suppose that f is a continuous function with compact support contained in [−2

, 2

]

for some N ∈ N. Deﬁne P

f(x) =

k=−n

∞

j=−∞

hf, ψ

iψ

(x).

(a) Show that P

f is the sum of only ﬁnitely many nonzero terms.

(b) If

f(x) dx = 0 =

−2

f(x) dx, then the only nonzero terms are for k ≥ −N.

Verify this. Show that P

f converges to f uniformly.

HINT: Modify Theorem 15.2.3.

f converges uniformly to f without the integral conditions.

HINT: Prove uniform convergence for ϕ

−N,0

and ϕ

−N,−1

F. Show that for f ∈ L

(R) that

∞

k=−∞

∞

j=0

hf, ψ

iψ

(x) =

[0,∞)

520 Wavelets

15.3. Multiresolution Analysis

Motivated by the Haar wavelet, we develop a general framework that applies

to a wide range of wavelet systems. We will use this framework to construct other

wavelet systems.

As before, ϕ =

[0,1)

and we deﬁne the translations and dilations

(x) = 2

k/2

ϕ(2

x − j) for all k, j ∈ Z.

This is not an orthonormal system. But for each k, the family {ϕ

: j ∈ Z}

consists of multiples of the characteristic functions of the dyadic intervals of length

−k

. In particular, these families are orthonormal.

Deﬁne V

= span{ϕ

: j ∈ Z}. This is the space of L

functions that are

constant on each dyadic interval of length 2

−k

. Consequently V

⊂ V

k+1

for k ∈ Z.

That is, the V

form a nested sequence of subspaces:

··· ⊂ V

−2

⊂ V

−1

⊂ V

⊂ ··· .

It is also immediate that f(x) belongs to V

if and only if f(2x) belongs to V

k+1

We state and prove the important (but basically easy) properties of this decomposi-

tion.

15.3.1. LEMMA. Let ϕ =

[0,1)

and deﬁne V

as above. Then we have

(1) orthogonality: {ϕ(x − j) : j ∈ Z} is an orthonormal basis for V

(2) nesting: V

⊂ V

k+1

for all k ∈ Z.

(3) scaling: f(x) ∈ V

if and only if f(2x) ∈ V

k+1

(4) density:

k∈Z

= L

(R).

(5) separation:

k∈Z

= {0}.

PROOF. We have already established (1), (2), and (3).

As in the proof of Theorem 15.2.3, we know that every continuous function

with compact support [−N, N ] is the uniform limit of functions that also have

support [−N, N ] and are constant on dyadic intervals of length 2

−k

, (i.e., functions

in V

). These functions therefore converge in L

as well. Consequently, the closed

union of the V

’s contains all continuous functions of compact support, and thus all

of L

(R).

Notice that ψ

is orthogonal to ϕ

provided that k ≥ k

because ϕ

will be

constant on the support of ψ

and ψ

integrates to 0. So any function f belonging

to the intersection

k∈Z

must be orthogonal to every ψ

. By Theorem 15.2.5, it

follows that f is orthogonal to every function in L

(R), including itself. Therefore,

kfk

= hf, f i = 0, whence f = 0. ¥

This leads us to formalize these properties in greater generality.

15.3 Multiresolution Analysis 521

15.3.2. DEFINITION. A multiresolution of L

(R) with scaling function ϕ is

the sequence of subspaces

= span

(x) = 2

k/2

ϕ(2

x − j) : j ∈ Z

provided that the sequence satisﬁes the ﬁve properties—orthogonality, nesting,

scaling, density and separation—described in the preceding lemma.

The function ϕ is sometimes called a father wavelet.

Notice that by a change of variables t = 2

x, we obtain

hϕ

, ϕ

i =

∞

−∞

ϕ(2

x − i)ϕ(2

x − j) dx

∞

−∞

ϕ(t − i)ϕ(t − j) dx = δ

So {ϕ

: j ∈ Z} forms an orthonormal basis of V

for each k ∈ Z.

Once we have a nested sequence V

with these properties, we can decompose

(R) into a direct sum of subspaces. Set W

= {f ∈ V

k+1

: f ⊥ V

}. This is the

orthogonal complement of V

in V

k+1

. We write V

k+1

= V

⊕ W

, where the ⊕

indicates that this is a direct sum, that is, a sum of orthogonal subspaces. So each

vector f ∈ V

k+1

can be written uniquely as f = g + h with g ∈ V

and h ∈ W

As hf, gi = 0, we have the Pythagorean identity

kfk

= hg + h, g + hi = hg, gi + hg, hi + hh, gi + hh, hi = kgk

+ khk

Since V

has an orthonormal basis {ϕ

: j ∈ Z}, Corollary 7.5.10 of Parse-

val’s Theorem provides an orthogonal projection P

of L

(R) onto V

given by

f =

∞

j=−∞

hf, ϕ

iϕ

and we have the important identity

kfk

= kP

+ kf − P

15.3.3. LEMMA. Q

= P

k+1

− P

is the orthogonal projection onto W

PROOF. To verify this, we will show that Q

is an idempotent with range W

and

kernel W

⊥

. Note that P

k+1

= P

k+1

= P

because V

is contained in V

k+1

Hence

= P

k+1

− P

k+1

− P

k+1

+ P

= P

k+1

− P

= Q

So Q

is a projection.

We claim that W

⊥

= V

⊥

k+1

. Indeed, P

⊥

k+1

f is orthogonal to V

k+1

and so is

also orthogonal to W

. So f is orthogonal to W

if and only if P

k+1

f is orthogonal

to W

, which is the same as saying that P

k+1

f ∈ V

. This latter statement is

equivalent to

k+1

f = P

k+1

f = P

f or (P

k+1

− P

)f = 0.

So W

⊥

= kerQ

522 Wavelets

If f ∈ W

, then P

k+1

f = f since f ∈ V

k+1

. Also, P

f = 0 since f ⊥ V

Hence Q

f = f. Conversely, if f = Q

g, then

k+1

f = P

k+1

g − P

k+1

g = (P

k+1

− P

)g = f.

So f belongs to V

k+1

. And

f = P

k+1

g − P

g = (P

− P

)g = 0.

Thus f is orthogonal to V

, and so f is in W

. Therefore, the range of Q

is exactly

. Consequently, Q

is the orthogonal projection onto W

. ¥

We may repeat the decomposition V

k+1

= V

⊕ W

ﬁnitely often to obtain

= V

⊕ W

⊕ ··· ⊕ W

n−1

and V

= V

−n

⊕ W

−n

⊕ ··· ⊕ W

−1

Repetition of this procedure suggests that there is a decomposition of L

(R) as an

inﬁnite direct sum

k∈Z

= ··· ⊕ W

−2

⊕ W

−1

⊕ W

⊕ ··· .

What we mean by this is that every function f in L

(R) should decompose uniquely

as an inﬁnite sum

f =

∞

k=−∞

where f

∈ W

and kfk

k∈Z

We shall prove that this is indeed the case.

15.3.4. LEMMA. Suppose that V

⊂ V

k+1

for k ∈ Z is the nested sequence of

subspaces from a multiresolution of L

(R). Then

lim

k→∞

kf − P

= 0, and lim

k→−∞

= 0.

PROOF. The limit lim

k→∞

kf − P

is a consequence of density. For any ε > 0,

there is an integer n and a function g ∈ V

such that kf −gk

< ε. Then for k ≥ n,

Parseval’s Theorem (Theorem 7.5.9) shows that

kf − P

= k(f − g) − P

(f − g)k

≤ kf − gk

< ε.

The second limit lim

k→−∞

= 0 is a consequence of separation. We will

show that it actually follows from the ﬁrst part. Let V

⊥

denote the orthogonal

complement of V

, and note that I −P

is the orthogonal projection onto it. Notice

that these subspaces are also nested in the reverse order V

⊥

k+1

⊂ V

⊥

. We claim that

N =

k∈Z

⊥

is all of L

(R). Indeed, if N were a proper subspace of L

(R),

then there would be a nonzero function g ⊥ N. Thus, in particular, g ⊥ V

⊥

so that g belongs to V

⊥⊥

= V

for every k ∈ Z. Consequently, g belongs to

k∈Z

= {0}. So N = L

(R). Since kP

= kf − (I − P

)fk

, the desired

limit follows from the ﬁrst part. ¥