Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


15.5 Daubechies Wavelets 533
–1
1
–1 1
2
FIGURE 15.4. The Daubechies wavelet.
D. Write out the details of the argument that
R
ϕ(x) dx = 1 implies that
P
j
a
j
= 2.
E. Define Q[
√
3] as the set of numbers x +
√
3y, where x, y ∈ Q.
(a) Show that if a +
√
3b = x +
√
3y, then a = x and b = y. Thus we can represent
elements of Q[
√
3] uniquely as ordered pairs.
(b) Show that addition, multiplication, and division operations in Q[
√
3] are closed and
can be expressed using rational operations.
(c) Explain the significance of this last fact for the efficiency of the algorithm for eval-
uating ϕ and ψ given at the end of this section.
F. Let ϕ be the Daubechies scaling function. Let D
n
be the set {a/2
k
: k ∈ N, a ∈ Z}
and define the set of dyadic rationals to be D = ∪
n≥1
D
n
. Further, define D
n
[
√
3] to
be the set {a +
√
3b : a, b ∈ D
n
} and likewise define D[
√
3].
(a) Show that for d ∈ D, ϕ(d) ∈ D[
√
3].
(b) If a +
√
3b is defined as a −
√
3b, show that for d ∈ D, ϕ(3 −d) = ϕ(d).
HINT: Prove it for D
n
using induction on n.
(c) Show that for d ∈ D, 1 =
X
k∈Z
ϕ(d − k). HINT: See the previous hint.
(d) Show that
3
X
k=0
kϕ(k) =
2
X
j=0
2ja
2j
=
3 −
√
3
2
.
(e) Show that for d ∈ D, d =
X
k∈Z
³
3 −
√
3
2
+ k
´
ϕ(d − k).
HINT: Using part (c), show that it is enough to prove d−
3 −
√
3
2
=
X
k∈Z
kϕ(d−k)
Then use induction, part (d), and considerable calculation.
(f) Using the continuity of ϕ, deduce that for all x ∈ R,
1 =
X
k∈Z
ϕ(x − k), x =
X
k∈Z
³
3 −
√
3
2
+ x
´
ϕ(x − k).

534 Wavelets
G. Suppose that ϕ is any scaling function of compact support arising from a multiresolu-
tion analysis and its scaling relation ϕ(x) =
P
j
a
j
ϕ(2x − j).
(a) Show that
P
n
ϕ(2
−k
n) = 2
k
P
n
ϕ(n) for all k ≥ 1.
(b) Show that
R
ϕ(x) dx =
P
n
ϕ(n). HINT: Use Riemann sums and part (a).
(c) Show that
P
n
ϕ(x − n) is constant.
H. Consider the sequence of functions ϕ
k0
(x) = 2
k/2
ϕ(2
k
x) for k ≥ 0, where ϕ is the
Daubechies scaling function. Compare this family of functions to the Fej
´
er kernel
(Definition 14.6.1). Precisely, which properties of Fej
´
er kernel (Theorem 14.6.3) carry
over directly to the functions ϕ
k0
? If a property does not carry over directly, is there
an analogous property that the functions ϕ
k0
have?
I. The construction used in this section can be extended to wavelets of higher order (i.e.,
with more moments vanishing).
(a) Use Equation (15.5.2) and
R
x
2
ψ(x) dx =
R
x
3
ψ(x) dx = 0 to derive two addi-
tional conditions on the sequence (a
k
).
(b) Show that the following values, with all other a
k
zero, give an approximate solution
to these conditions.
a
0
= .470467 a
1
= 1.141117 a
2
= .650365
a
3
= −.190934 a
4
= −.120832 a
5
= .049817
(c) Using the appropriate scaling relation, plot these higher-order wavelets and scaling
functions. Although the graph suggests otherwise, this scaling function is actually
differentiable.
15.6. Existence of the Daubechies Wavelet
The purpose of this section is to establish the following:
15.6.1. THEOREM. The sequence of functions (ϕ
n
) converges in the L
2
(R)
norm to a function ϕ.
We need two computational lemmas that enable us to estimate kϕ
n+1
− ϕ
n
k
2
.
First, we compute hϕ
n+1
(x), ϕ
n
(x − k)i.
15.6.2. LEMMA. Define c
n
(k) = hϕ
n+1
, ϕ
n
(x − k)i for k ∈ Z and n ≥ 0.
Then c
n
(k) = 0 if |k| > 2, and the sequence of 5-tuples
c
n
=
¡
c
n
(−2), c
n
(−1), c
n
(0), c
n
(1), c
n
(2)
¢
for n ≥ 0
satisfies c
0
= (0, 0,
2+
√
3
4
,
2−
√
3
4
, 0) and c
n+1
= T c
n
, where
T =
0 −1/16 0 0 0
1 9/16 0 −1/16 0
0 9/16 1 9/16 0
0 −1/16 0 9/16 1
0 0 0 −1/16 0
.

15.6 Existence of the Daubechies Wavelet 535
PROOF. Since ϕ
0
=
χ
[0,1)
and
ϕ
1
=
3
X
i=0
a
i
ϕ
0
(2x − i) = a
0
χ
[0,.5)
+ a
1
χ
[.5,1)
+ a
2
χ
[1,1.5)
+ a
3
χ
[1.5,2)
we easily compute c
0
(0) =
a
0
+ a
1
2
=
2 +
√
3
4
and c
0
(1) =
a
2
+ a
3
2
=
2 −
√
3
4
and c
0
(k) = 0 in all other cases. Proceed by induction on n.
c
n+1
(k) = hϕ
n+1
, ϕ
n
(x − k)i
=
D
3
X
i=0
a
i
ϕ
n
(2x − i),
3
X
j=0
a
j
ϕ
n−1
(2x − 2k − j)
E
=
3
X
i=0
3
X
j=0
a
i
a
j
ϕ
n
(2x − i), ϕ
n−1
(2x − 2k − j)
®
Notice that making the substitution y = 2x − i in the inner product results in a
factor of
1
2
from the change of variable of integration.
=
1
2
3
X
i=0
3
X
j=0
a
i
a
j
ϕ
n
(y), ϕ
n−1
(y + i − 2k − j)
®
Now set l = j − i to obtain
=
1
2
3
X
i=0
3
X
l=−3
a
i
a
i+l
ϕ
n
(y), ϕ
n−1
(y − 2k − l)
®
=
3
X
l=−3
³
1
2
3
X
i=0
a
i
a
i+l
´
c
n−1
(2k + l).
Observe immediately that if |k| ≥ 3 and |l| ≤ 3, then |2k + l| ≥ 3. Therefore,
c
n+1
(k) for |k| ≥ 3 depend linearly on c
n
(k) for |k| ≥ 3. However, c
0
(k) = 0 for
|k| ≥ 3, so c
n
(k) = 0 for all n ≥ 0 and |k| ≥ 3. So we need only be concerned
with the 5-tuple c
n
=
¡
c
n
(−2), c
n
(−1), c
n
(0), c
n
(1), c
n
(2)
¢
.
A routine calculation yields
1
2
3
X
i=0
a
i
a
i+l
=
1 when l = 0
9/16 when l = ±1
−1/16 when l = ±3
0 otherwise.
Plugging this into our identity and writing the five relations as a matrix, we obtain
c
n+1
= T c
n
. ¥
536 Wavelets
Next we compute the Jordan form of T . Note immediately that T e
0
= e
0
is an
obvious eigenvector.
15.6.3. LEMMA. The matrix T factors as T = V JV
−1
, where
V =
0 −1 2 −1 4
0 8 −4 4 0
1 0 0 −6 −8
0 −8 4 4 0
0 1 −2 −1 4
and J =
1 0 0 0 0
0 1/2 0 0 0
0 0 1/8 0 0
0 0 0 1/4 1
0 0 0 0 1/4
.
PROOF. We leave it to the reader to show that V J = T V and to check that V is
invertible (see the formula for V
−1
given in the proof of Theorem 15.6.4). ¥
15.6.4. THEOREM.
P
n≥0
kϕ
n+1
−ϕ
n
k
2
< ∞ and thus lim
n→∞
ϕ
n
exists in L
2
(R).
PROOF. The first step is to compute c
n
(0). Notice that c
n
= T
n
c
0
= V J
n
V
−1
c
0
.
We find that
J
n
=
1 0 0 0 0
0 2
−n
0 0 0
0 0 8
−n
0 0
0 0 0 4
−n
4
1−n
n
0 0 0 0 4
−n
and V
−1
=
1 1 1 1 1
1
6
1
12
0 −
1
12
−
1
6
1
3
1
24
0 −
1
24
−
1
3
0
1
8
0
1
8
0
1
8
1
32
0
1
32
1
8
.
Thus a straightforward multiplication yields
hϕ
n+1
, ϕ
n
i = c
n
(0) = 1 −4
−n−2
(2 −
√
3)(3n + 4).
Set ε
n
= 4
−n−2
(2 −
√
3)(3n + 4). Notice that
kϕ
n+1
− ϕ
n
k
2
= hϕ
n+1
− ϕ
n
, ϕ
n+1
− ϕ
n
i
= kϕ
n+1
k
2
2
− 2hϕ
n+1
, ϕ
n
i + kϕ
n
k
2
2
= 2 − 2(1 −ε
n
) = 2ε
n
.
Consequently,
X
n≥0
kϕ
n+1
− ϕ
n
k
2
=
X
n≥0
q
2(2 −
√
3)(3n + 4)
2
n+2
<
X
n≥0
n + 2
2
n+2
=
3
2
.
By Exercise 4.2.B, this implies that (ϕ
n
) is a Cauchy sequence. Thus the limit
function ϕ is defined. ¥

15.7 Approximations Using Wavelets 537
Exercises for Section 15.6
A. Verify that V J = T V and that the formula for V
−1
is correct.
B. Do the calculation to compute c
n
(0) as indicated in Theorem 15.6.4.
C. Verify that
P
n≥0
n + 2
2
n+2
converges. Do not compute its exact value.
D. Observe that the columns of T all sum to 1. Interpret this as saying that a related
matrix has a certain eigenvector.
E. Find lim
n→∞
T
n
. HINT: Use the Jordan form.
15.7. Approximations Using Wavelets
In this section, we approximate functions using the Daubechies wavelet sys-
tem. Our goal is to show how properties of the wavelet basis result in better (or
worse) approximations. Given that the point of wavelets is to use different kinds of
wavelets for different problems, it is worthwhile to see how to use properties of the
wavelet and scaling function. We have already devoted Chapter 14 to approxima-
tion by Fourier series and Chapter 10 to approximation by polynomials, so we can
compare approximation by wavelets to these alternatives.
Recall from the discussion of Haar wavelets that we may construct approx-
imants to functions by first computing the projection P
k
f of f onto V
k
. Let ϕ
and {ψ
kj
} denote the Daubechies wavelet. Let us define the projections D
n
onto
V
n
= span{ϕ
n,j
: j ∈ Z} by
D
n
f(x) =
X
j∈Z
hf, ϕ
n,j
iϕ
n,j
.
For n ≥ 1, we also realize this as
D
n
f(x) = D
0
f(x) +
n−1
X
k=0
X
j∈Z
hf, ψ
kj
iψ
kj
(x).
If f has compact support, then only finitely many of these coefficients are nonzero
at each level. For example, if the support is [0, 1], then there are at most three
nonzero terms in the computation of D
0
and at most 2
n−1
+ 2 additional terms to
compute D
n
f knowing D
n−1
f.
For any wavelet arising from a multiresolution analysis, the approximants P
k
f
converge to f in L
2
(R). So, in particular, this is true for the Daubechies wavelets.
In this case, we can also establish uniform convergence when f is uniformly con-
tinuous. We need a variation on the first part of the proof of Theorem 15.2.3.
15.7.1. LEMMA. Consider the Daubechies wavelets. Fix k ∈ N, j ∈ Z, and
x ∈ [j/2
k
, (j + 3)/2
k
]. For any continuous function f on R,
¯
¯
f(x) − 2
k/2
hf, ϕ
kj
i
¯
¯
≤
√
3ω(f, 3 · 2
−k
).
538 Wavelets
PROOF. Using the substitution z = 2
k
t − j and
R
ϕ(t) dt = 1, we have
¯
¯
f(x) − 2
k/2
hf, ϕ
k0
i
¯
¯
=
¯
¯
¯
f(x) − 2
k
Z
f(t)ϕ(2
k
t − j) dx
¯
¯
¯
=
¯
¯
¯
f(x) −
Z
3
0
f
³
z + j
2
k
´
ϕ(z) dz
¯
¯
¯
=
¯
¯
¯
Z
3
0
h
f(x) − f
³
z + j
2
k
´i
ϕ(z) dz
¯
¯
¯
≤ ω(f; 3 ·2
−k
)
Z
3
0
|ϕ(z)|dz
since for z ∈ [0, 3], we have |x−(z+j)/2
k
| ≤ 3/2
k
. Finally, the Cauchy–Schwarz
inequality shows that
Z
3
0
|ϕ(z)|dz ≤
³
Z
3
0
|ϕ(z)|
2
dz
´
1/2
³
Z
3
0
1dz
´
1/2
=
√
3.
¥
15.7.2. THEOREM. If f ∈ L
2
(R) is uniformly continuous on R, then the ap-
proximants D
k
f by Daubechies wavelets converge uniformly to f.
PROOF. From Exercise 15.5.G, we have
P
j∈Z
ϕ(2
k
x − j) = 1. Multiplying this by
f(x), we have
|f(x) − D
k
f(x)| =
¯
¯
¯
X
j∈Z
f(x)ϕ(2
k
x − j) −
X
j∈Z
hf, ϕ
kj
iϕ
kj
(x)
¯
¯
¯
≤
X
j∈Z
¯
¯
f(x) − 2
k/2
hf, ϕ
kj
i
¯
¯
¯
¯
ϕ(2
k
x − j)
¯
¯
≤
√
3ω(f, 3 · 2
−k
)
X
j∈Z
|ϕ(2
k
x − j)|
≤ 3
√
3kϕk
∞
ω(f, 3 · 2
−k
),
because for any x, there at most three j so that ϕ(2
k
x − j) 6= 0. By the uniform
continuity of f, lim
k→∞
ω(f, 3 · 2
−k
) = 0. Thus lim
k→∞
kf − D
k
f(x)k
∞
= 0. ¥
15.7.3. REMARK. This proof does something even better because of the local
nature of the Daubechies wavelets. If f is not continuous everywhere, but is con-
tinuous on a neighbourhood [a −δ, a + δ], the same argument shows that the series
converges uniformly on [a−ε, a+ε] for ε < δ. We will use this in Example 15.7.4.
Theorem 15.2.3 likewise shows that when f is continuous, H
n
f converges to
f uniformly. In fact, kH
n
f − fk
∞
≤ ω(f;2
−n
). So if f has Lipschitz constant
L, the error is at most 2
−n
L. Since the number of coefficients in H
n
f doubles

15.7 Approximations Using Wavelets 539
when n increases by 1, this is not surprising. We now have a comparable rate of
convergence for Daubechies wavelets.
In approximating a function, a reasonable measure of the size of the approxi-
mant is the number of coefficients used. For f ∈ L
2
(0, 1), we have
H
n
f(x) = hf, ϕiϕ(x) +
n−1
X
k=0
2
k
−1
X
j=0
hf, ψ
kj
iψ
kj
(x)
and so H
n
f uses 2
n
coefficients. If there is a bound on the number of coefficients
that we can use, due to storage limitations, for example, one choice is to use the
largest value of n so that H
n
f does not have too many coefficients. It is frequently
better to use a larger value of n and then replace small coefficients with zero. This
has the advantage that if f has large irregularities at small resolution, these will
appear in the approximation.
15.7.4. EXAMPLE. Consider the function given by
f(x) =
(
x if x ∈ (−π, π),
0 if |x| ≥ π.
In Section 14.5, we analyzed the how the partial sums S
n
f of the Fourier series
approximated f near the discontinuity at π. The Fourier series for f on (−π, π) is
f(x) ∼ 2
∞
X
k=1
(−1)
k+1
k
sinkx,
which converges very slowly. Even at a point well away from the discontinuity,
convergence is slow. For example, if x = π/2, then we get
f(π/2) = 2
∞
X
k=0
(−1)
k
2k + 1
.
To get 2
n
P
k=0
(−1)
k
/(2k + 1) within 10
−6
of the exact sum of the series, we need
n ≥ 500, 000. (To be fair, we can do better with Fej
´
er kernels, but the behaviour is
not optimal even then.)
The Haar wavelet approximations H
n
f are the step functions taking the av-
erage value of f over each interval of length 2
−n
. It is not difficult to see that
except for two intervals about the discontinuities ±π, the convergence is uniform.
The maximum error is 2
−n−1
. Since the number of coefficients needed is roughly
2
n+1
π, we see that this convergence is not much more efficient than the Fourier se-
ries globally. However, to compute f(π/2), note that only n terms in the expansion
H
n
f are nonzero at π/2. Thus to compute this value within 10
−6
, we only need 19
terms since 2
−20
< 10
−6
.
Even better, the vanishing moments of the Daubechies wavelets ensure that so
long as the support of ψ
kj
does not contain ±π, thecoefficient hf, ψ
kj
iwill be zero.
Since ψ has support in [0, 3], each ψ
kj
has support in an interval of length 3/2
k
,

540 Wavelets
namely [j/2
k
, (j + 3)/2
k
]. So for each k, there are only six nonzero coefficients
for ψ
kj
to contribute to the whole series.
Returning to the point π/2, notice that for the support of ψ
kj
to contain both
π/2 and π, we must have 3 · 2
−k
> π/2 or k ≤ 0. Thus D
0
f(π/2) = D
n
f(π/2)
for all n ∈ N. Indeed by Remark 15.7.3, this series converges uniformly to f on
any interval around π/2 that is bounded away from ±π. In particular, we have
f(π/2) = lim
n→∞
D
n
f(π/2) = D
0
f(π/2). So only three nonzero coefficients are
involved in recovering this value exactly.
We can use the vanishing of the moments to obtain a better bound when the
function f is C
2
. Thus as for Fourier series, the Daubechies wavelet coefficients
will die off quickly if the function is smooth. Moreover, because of the local nature
of these wavelets, if f is smooth on some small interval, the same analysis shows
that the wavelet series converges rapidly on that interval.
15.7.5. THEOREM. If f is twice differentiable on [(j − 2)/2
k
, (j + 2)/2
k
],
where j, k ∈ Z, and f
00
bounded by B on this interval, then
¯
¯
hf, ψ
kj
i
¯
¯
≤
4B
2
5k/2
.
PROOF. Substituting t = 2
k
x − j, we obtain
hf, ψ
kj
i =
Z
+∞
−∞
f(x)2
k/2
ψ(2
k
x − j) dx = 2
−k/2
Z
+∞
−∞
f
³
t + j
2
k
´
ψ(t) dt.
This integral may be limited to [−1, 2], the support of ψ.
On [(j − 2)/2
k
, (j + 2)/2
k
], we have a Taylor series expansion for f centred
at the point b = j/2
k
, namely
f(x) = f(b) + f
0
(b)(x − b) +
f
00
(c)
2
(x − b)
2
for some point c between x and b. The vanishing moment conditions on ψ imply
that
R
(mx + d)ψ(x) dx = 0. As x − b = (t + j)/2
k
− j/2
k
= t/2
k
, we end up
with
hf, ψ
kj
i = 2
−k/2
1
2
f
00
(c)
Z
2
−1
³
t
2
k
´
2
ψ(t) dt.
Since t
2
≤ 4, we obtain
¯
¯
hf, ψ
kj
i
¯
¯
≤
2B
2
5k/2
Z
2
−1
|ψ(t)|dt.
Finally, the Cauchy–Schwarz inequality shows that
Z
2
−1
|ψ(t)|dt ≤
³
Z
2
−1
|ψ(t)|
2
dt
´
1/2
³
Z
2
−1
1dt
´
1/2
=
√
3 < 2.
¥
15.8 The Franklin Wavelet 541
Exercises for Section 15.7
A. Show that
°
°
°
b
0
ϕ +
n−1
P
k=0
2
k
−1
P
j=0
a
kj
ψ
kj
°
°
°
∞
≤ |b
0
| +
n−1
P
k=0
3 · 2
k/2
max
©
|a
kj
| : j ∈ Z
ª
.
HINT: For each x and k, how many ψ
kj
(x) 6= 0?
B. Recall the Cantor function f on [0, 1] from Example 5.7.8. Find the zero coefficients
hf, ψ
kj
i for k = 1, 2, 3, 4. What can you conclude about the functions D
n
f?
C. (a) For the function f in Example 15.7.4, find the least k ∈ N so that f (3) = D
k
f(3).
(b) In general, find a function K(δ) so that for k ≥ K(δ), f(π − δ) = D
k
f(π − δ).
D. For the higher-order Daubechies wavelets of Exercise 15.5.I, state and prove a version
of Theorem 15.7.5.
E. Given a function f, we can represent P
n
f in two ways: b
0
ϕ +
n−1
P
k=0
P
j∈Z
a
kj
ψ
kj
or
P
j∈Z
c
j
ϕ
nj
.
(a) For the Haar wavelets, what is the significance of the coefficients b
0
and a
kj
?
(b) For the Haar wavelets, describe how to obtain one set of coefficients from the other.
HINT: Exercise 15.2.A.
(c) For the Daubechies wavelets, describe how to obtain one set of coefficients from
the other.
15.8. The Franklin Wavelet
It is not easy to just write down a wavelet or a scaling function. However, it is
much easier to find a multiresolution with a scaling function that does not generate
an orthonormal basis but does something a bit weaker. The goal is to construct a
continuous piecewise linear wavelet by starting with such a system. The technique
that we describe here can be adapted and refined to obtain wavelets with greater
smoothness and/or with compact support. In this section, we restrict our attention
to a single example known as the Franklin wavelet.
In these last sections, we need to take a more sophisticated view of linear maps
between Hilbert spaces.
Consider the subspaces V
k
of L
2
(R) consisting of continuous functions in
L
2
(R) that are linear on each interval [(j − 1)2
−k
, j2
−k
]. These subspaces sat-
isfy most of the requirements of a multiresolution. It is immediately evident that
V
k
is contained in V
k+1
for all k ∈ Z. Also by definition, f(x) belongs to V
k
ex-
actly when it is continuous and linear on each dyadic interval of length 2
−k
, which
holds precisely when f (2x) is continuous and linear on each dyadic interval of
length 2
−k−1
, which means that f(2x) belongs to V
k+1
. So the V
k
satisfy scaling.
The union of the V
k
’s is dense in all of L
2
(R). To see this, note that any
continuous function g with bounded support, say contained in [−2
N
, 2
N
], may be
uniformly approximated to any desired accuracy by a piecewise linear continuous
542 Wavelets
function f that is linear on dyadic intervals of length 2
−k
provided that k is suffi-
ciently large. Given ε > 0, choose k and f ∈ V
k
so that f is also supported on
[−2
N
, 2
N
] and kg − fk
∞
< 2
−(N+1)/2
ε. It is easy to see that
kg − fk
2
2
=
Z
2
N
−2
N
|g(x) − f(x)|
2
dx ≤
Z
2
N
−2
N
¡
2
−(N+1)/2
ε
¢
2
dx = ε
2
.
Because C
c
(R) is dense in L
2
(R), it follows that we have the density property
S
k∈Z
V
k
= L
2
(R).
Finally, we will demonstrate the separation property
T
k∈Z
V
k
= {0}. Suppose
that f belongs to this intersection. Let f(i) = a
i
for i = −1, 0, 1. Since f ∈ V
−k
for each k > 0, it is linear on [0, 2
k
] and on [−2
k
, 0]. So f(x) = a
0
+ (a
1
− a
0
)x
on [0, 2
k
] and f (x) = a
0
− (a
−1
− a
0
)x on [−2
k
, 0]. Thus
kfk
2
2
≥
Z
2
k
0
|f(x)|
2
dx =
1
3
(a
1
− a
0
)
2
x
3
+ a
0
(a
1
− a
0
)x
2
+ a
2
0
x
¯
¯
¯
2
n
0
=
1
3
(a
1
− a
0
)
2
2
3n
+ a
0
(a
1
− a
0
)2
2n
+ a
2
0
2
n
= 2
n
³
1
3
¡
(a
1
− a
0
)2
n
+
3
2
a
0
¢
2
+
1
4
a
2
0
´
.
As n tends to infinity, the right-hand side must remain bounded by kfk
2
2
. This
forces a
0
= a
1
= 0. Likewise, integration from −2
k
to 0 shows that a
−1
= 0.
Consequently f = 0 on [−2
k
, 2
k
] for every k ≥ 0. So f = 0 and the intersection
is trivial.
We have constructed a multiresolution except for the important scaling func-
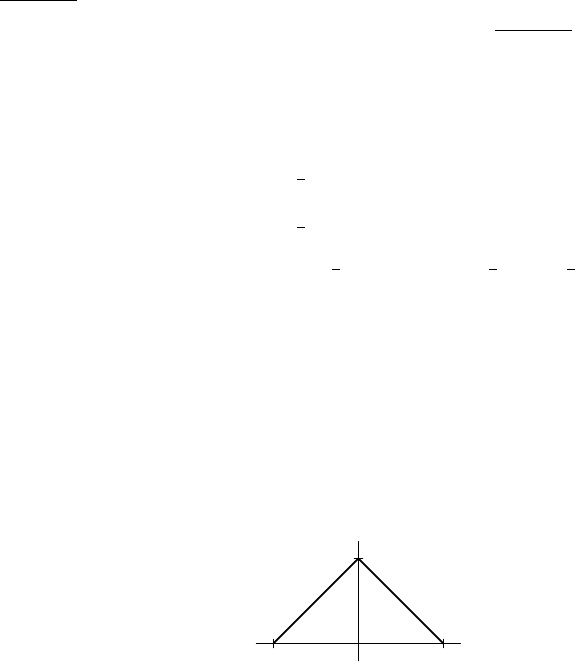
tion. There is a function h, known as the hat function, which has all but one of
the properties of a scaling function. It is supported on [−1, 1], has h(0) = 1 and
h(−1) = h(1) = 0, and is linear in between. Figure 15.5 gives its simple graph.
x
0
1−1
y
1
FIGURE 15.5. The graph of the hat function h.
Notice that f(x) =
n
P
j=−n
a
j
h(x − j) is the piecewise linear function in V
0
,
which is supported on [−n −1, n + 1] and satisfies f(j) = a
j
for −n ≤ j ≤ n and
f(j) = 0 for |j| > n. So V
0
is spanned by translates of the hat function. Likewise,
V
k
is spanned by
©
2
k/2
h(2
k
x − j) : j ∈ Z
ª
. The problem with h is that these
translates are not orthogonal to each other. But it does have a weaker property that
serves as a substitute.
