Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

16.1 Convex Sets 563

F. Suppose that A is a convex subset of R

and that T is a linear transformation from R

into R

. Prove that T A is convex and aff(TA) = T aff(A).

G. If A ⊂ R

and B ⊂ R

, then A × B := {(a, b) ∈ R

m+n

: a ∈ A, b ∈ B}. Show

that conv(A × B) = conv(A) × conv(B).

H. (a) If S is a bounded subset of R

, prove that conv(S) is bounded.

(b) Give an example of a closed subset S of R

such that conv(S) is not closed.

I. Recall that the graph of f : R

→ R

is G(f) = {(x, y) ∈ R

× R

: f(x) = y}.

Show that f is a linear function if and only if G(f) is a linear subspace of R

m+n

and

f is an afﬁne function if and only if G(f) is an afﬁne set.

J. A function f on R is convex if f

λx + (1 − λ)y

≤ λf (x) + (1 − λ)f(y) for all

x, y ∈ R and 0 ≤ λ ≤ 1. If f is any function on R, deﬁne the epigraph of f to be

epi(f) = {(x, y) ∈ R

: y ≥ f(x)}. Show that f is a convex function if and only if

epi(f) is a convex subset of R

K. Let A and B be convex subsets of R

. Prove that conv(A ∪B) equals the union of all

line segments [a, b] such that a ∈ A and b ∈ B.

L. The asymptotic cone. Let A ⊂ R

be closed and convex, and x ∈ A.

(a) Show that s(A − x) ⊂ t(A − x) if 0 < s < t.

(b) Show that A

∞

(x) =

t>0

t(A − x) := {d : x + td ∈ A for all t > 0} is a cone.

∞

(x) does not depend on the point x.

HINT: Consider (1 −

)y +

(x + ktd).

(d) Prove that A is compact if and only if A

∞

= {0}.

HINT: If ka

k → ∞, ﬁnd a cluster point d of a

/ka

k. Argue as in (c).

M. A set S ⊂ R

is a star-shaped set with respect to v ∈ S if [s, v] ⊂ S for all s ∈ S.

(a) Show that S is convex if and only if it is star shaped with respect to every v ∈ S.

(b) Find a set that is star shaped with respect to exactly one of its points.

N. (a) Given a sequence of convex sets B

⊂ B

··· in R

, show that

i≥1

convex.

(b) For any sequence of convex sets B

, B

, . . . in R

, show that

j≥1

(

i≥j

)

is convex.

O. A set S ⊂ R

is called afﬁnely dependent if there is an s ∈ S so that s ∈ aff(S\{s}).

Show that S is afﬁnely dependent if and only if there are distinct elements s

, . . . , s

of S and scalars µ

, . . . , µ

, not all zero, so that

i=1

= 0 and

i=1

= 0.

HINT: Solve for some s

P. A subset S ⊂ R

is afﬁnely independent if it is not afﬁnely dependent. Show that an

afﬁnely independent set in R

can have at most n + 1 points.

HINT: If {s

, . . . , s

} ⊂ S, show that {s

− s

: 1 ≤ i ≤ n} is linearly independent.

Q. Radon’s Theorem. Suppose that s

, . . . , s

are distinct points in R

, with r > n + 1.

Show that there are disjoint sets I and J with I ∪ J = {1, . . . , r} so that the convex

sets conv{s

: i ∈ I} and conv{s

: j ∈ J} have nonempty intersection.

HINT: Use the previous two exercises to obtain 0 as a nontrivial linear combination of

these elements. Then consider those elements with positivecoefﬁcients in this formula.

564 Convexity and Optimization

R. Helly’s Theorem. Let C

be convex subsets of R

for 1 ≤ k ≤ m. Suppose that any

n + 1 of these sets have nonempty intersection. Prove that the whole collection has

nonempty intersection.

HINT: Use induction on m ≥ n+1 sets. If true for m−1, choose x

in the intersection

of C

, . . . , C

j−1

, C

j+1

, . . . , C

. Apply Radon’s Theorem.

16.2. Relative Interior

In workingwith a convex subset A of R

, the natural space containing it is often

aff(A), not R

, which may be far too large. The afﬁne hull is a better place to work

for many purposes. Indeed, if A is a convex subset of R

with dimA = k < n,

then thinking of A simply as a subset of aff(A), which may be identiﬁed with R

allows us to talk more meaningfully about topological notions such as interior and

boundary. One sign that the usual interior is not useful is Exercise 16.1.D, which

shows that A has empty interior when dim(A) < n. This section is devoted to

developing the properties of the interior relative to aff(A).

16.2.1. DEFINITION. If A is a convex subset of R

, then the relative interior

of A, denoted ri(A), is the interior of A relative to aff(A). That is, a ∈ ri(A) if and

only if there is an ε > 0 so that B

(a) ∩ aff(A) ⊂ A.

Deﬁne the relative boundary of A, denoted rbd(A), to be

A \ ri(A).

16.2.2. EXAMPLE. If dimA = k < n, then ri(A) is the interior of A when

A is considered as a subset of aff(A), which is identiﬁed with R

. For example,

consider the closed convex disk A = {(x, y, z) ∈ R

: x

+ y

≤ 1, z = 0}.

Then aff(A) = {(x, y, z) ∈ R

: z = 0} is a plane. The relative interior of A is

ri(A) = {(x, y, z) ∈ R

: x

+ y

< 1, z = 0}, the interior of the disk in this

plane, while the interior as a subset of R

is empty. The relative boundary is the

circle {(x, y, z) ∈ R

: x

+ y

= 1, z = 0}.

Notice that A ⊂ B does not imply that ri(A) ⊂ ri(B) because an increase in

dimension can occur. For example, let B = {(x, y, z) : x

+ y

≤ 1, z ≤ 0}. Then

ri(B) = int(B) = {(x, y, z) : x

+ y

< 1, z < 0}. So A ⊂ B but ri(A) and ri(B)

are disjoint.

The following result shows that the phenomenon above occurs precisely be-

cause of the dimension shift. Despite its trivial proof, it will be quite useful.

16.2.3. LEMMA. Suppose that A and B are convex subsets of R

with A ⊂ B.

If aff(A) = aff(B), then ri(A) ⊂ ri(B).

PROOF. If a ∈ ri(A), then there is an ε > 0 with B

(a) ∩ aff(A) ⊂ A. Because

aff(B) = aff(A), we have B

(a) ∩ aff(B) ⊂ A ⊂ B, so a ∈ ri(B). ¥

16.2 Relative Interior 565

A polytope is the convex hull of a ﬁnite set. Now we obtain an analogue of

Theorem 16.1.7 describing the relative interior of a polytope.

16.2.4. LEMMA. Let S = {s

, . . . , s

} be a ﬁnite subset of R

. Then

conv(S)

i=1

: λ

∈ (0, 1),

i=1

= 1

PROOF. By Theorem 16.1.7, conv(S) =

: λ

∈ [0, 1],

= 1

. The

subspace L(S) is given by Exercise 16.1.E as L(S) =

= 0

Let e

, . . . , e

be an orthonormal basis for L(S). Express each e

as a com-

bination e

, where

= 0, and deﬁne Λ = max

1/2

Suppose that x is vector in L(S). Then

x =

j=1

i=1

j=1

By the Schwarz inequality (4.1.1),

j=1

≤

j=1

1/2

j=1

1/2

≤ Λkxk.

Thus if kxk < ε/Λ, then x may be expressed as x =

, where

= 0

and |µ

| < ε for 1 ≤ i ≤ r.

Let a =

, where λ

∈ (0, 1) and

= 1. Then there is an ε > 0 so

that ε ≤ λ

≤ 1 − ε for 1 ≤ i ≤ r. Note that

ε/Λ

(a) ∩ aff(S) = a +

ε/Λ

(0) ∩ L(S)

If x ∈ L(S) and kxk < ε/Λ, we use the representation above to see that

a + x =

i=1

(λ

+ µ

Now

+ µ

= 1 and λ

+ µ

∈ [ε, 1−ε] + (−ε, ε) = (0, 1). So a + x belongs

to conv(S). This shows that a belongs to ri(conv(S)).

Conversely, suppose that a ∈ ri(S). Write a =

, where λ

∈ [0, 1] and

= 1. We wish to show that it has a possibly different representation with

coefﬁcients in (0, 1). Let ε > 0 be given so that B

ε/Λ

(a) ∩ aff(S) ⊂ conv(S). If

each λ

∈ (0, 1), there is nothing to prove. Suppose that J = {j : λ

= 0} is

nonempty, and let k be chosen so that λ

> 0. Pick a δ > 0 so small that |J|δ < λ

and x = δ

j∈J

−s

) satisﬁes kxk < ε. Then a ±x belong to conv(S). Write

a − x =

, where µ

∈ [0, 1] and

= 1. Also,

a + x =

j∈J

δs

+ (λ

− |J|δ)s

i∈(J∪{k})

i=1

566 Convexity and Optimization

It is evident from our construction that each ν

> 0; and since

= 1, all are

less than 1. Now a =

+ ν

is expressed with all coefﬁcients in (0, 1). ¥

16.2.5. COROLLARY. If A is a nonempty convex subset of R

, then ri(A) is

also nonempty. Moreover, aff(ri(A)) = aff(A).

PROOF. Let k = dimconv(A). Then there is a subset S of k + 1 points so that

aff(S) = aff(A). Indeed, ﬁx any element a

∈ A. Since L(A) is spanned by

{a − a

: a ∈ A} and has dimension k, we may choose k vectors a

, . . . , a

in A such that a

− a

are linearly independent. Clearly, they span L(A). So

S = {a

, . . . a

} will sufﬁce.

Hence, by Lemma 16.2.3, ri(convA) contains ri(convS). Let a =

k+1

i=0

By Lemma 16.2.4, ri(convS) is nonempty and, in particular, contains the points

= (a + 2a

)/3 and c

= (2a + a

)/3 for 0 ≤ i ≤ k. So aff(ri(conv S)) contains

− c

= a

for 0 ≤ i ≤ k, whence it equals aff(A) as claimed. ¥

The next theorem will be surprisingly useful. In particular, this theorem applies

if b is in the relative boundary, rbd(A).

16.2.6. ACCESSIBILITY LEMMA.

Suppose that A is a convex subset of R

. If a ∈ ri(A) and b ∈

A, then [a, b) is

contained in ri(A).

PROOF. Let ε > 0 be given so that B

(a) ∩ aff(A) ⊂ A. We need to show

that λa + (1 − λ)b ∈ ri(A) for λ ∈ (0, 1). Since b ∈ A, pick c ∈ A so that

x = b − c ∈ L(A) satisﬁes kxk < ελ/(2 − 2λ). Suppose that z ∈ L(A) with

kzk < ε/2. Then

λa + (1 −λ)b + λz = λa + (1 − λ)(c + x) + λz

= λ(a + z + (1 −λ)x/λ) + (1 − λ)c.

Since kz + (1 − λ)x/λk ≤ kzk + (1 − λ)kxk/λ < ε/2 + ε/2 = ε, this is a

vector in B

(0) ∩ L(A). Hence d = a + z + (1 − λ)x/λ belongs to A. Thus

λa + (1 − λ)b + λz = λd + (1 − λ)c also lies in A. So a + (1 − λ)b belongs to

ri(A). ¥

Applying the preceding result when b ∈ ri(A) shows that ri(A) is convex.

Since int(A) is either the empty set or equal to ri(A), we have the following:

16.2.7. COROLLARY. If A is a convex subset of R

, so are ri(A) and int(A).

16.2.8. THEOREM. If A is a convex subset of R

, then the three sets ri(A), A,

and A all have the same afﬁne hulls, closures, and relative interiors.

16.2 Relative Interior 567

PROOF. By Corollary 16.2.5, aff(ri(A)) = aff(A). Since the afﬁne hull is closed,

A ⊂ aff(A) and hence aff(A) = aff(A).

Now ri(A) ⊂ A ⊂ A, and so ri(A) ⊂ A = A, where the equality follows from

Proposition 4.3.5. Suppose that b ∈ A. By Corollary 16.2.5, ri(A) contains a point

a. Hence by the Accessibility Lemma (Lemma 16.2.6), λa + (1 − λ)b belongs to

ri(A) for 0 < λ ≤ 1. Letting λ tend to 0 shows that b ∈

ri(A). Thus ri(A) = A.

For relative interiors, ﬁrst observe that since the three sets have the same afﬁne

hull, Lemma 16.2.3 shows ri(ri(A)) ⊂ ri(A) ⊂ ri(A). Now ri(ri(A)) = ri(A). For

if a ∈ ri(A) and x ∈ B

(a) ∩ aff(A) ⊂ A, then using r = ε − kx − ak > 0,

it follows that B

(x) ∩ aff(A) ⊂ B

(a) ∩ aff(A) ⊂ A. Hence B

(a) ∩ aff(A) is

contained in ri(A) and so a ∈ ri(ri(A)).

Suppose that a ∈ ri(

A). Then there is an ε > 0 so that B

(a) ∩ aff(A) ⊂ A.

Pick anyb ∈ ri(A), and set x = (a−b)/ka−bk. Then c

= a±εx belong to A. But

−

= (1 −ε)a + εb ∈ ri(A) by the Accessibility Lemma. Hence a = (c

+ c

−

)/2

belongs to ri(A), again by the Accessibility Lemma. Therefore, ri(A) = ri(A). ¥

The next two results will allow us to conveniently compute various combina-

tions of convex sets such as sums and differences. The ﬁrst is quite straightforward

and is left as an exercise.

16.2.9. PROPOSITION. If A ⊂ R

and B ⊂ R

are convex sets, then A × B

is convex, ri(A × B) = ri(A) × ri(B) and aff(A × B) = aff(A) × aff(B).

16.2.10. THEOREM. If A is a convex subset of R

and T is a linear map from

to R

, then T ri(A) = ri(T A).

PROOF. By Exercise 16.1.F, T A is convex. Using Theorem 16.2.8 for the ﬁrst

equality and the continuity of T (see Corollary 5.1.7) for the second containment,

we have

T A ⊂ T A = T ri(A) ⊂ T ri(A) ⊂ T A.

Taking closures, we obtain T ri(A) = T A. Using Theorem 16.2.8 again,

ri(T A) = ri(T A) = ri(T ri(A)) = ri(T ri(A)) ⊂ T ri(A).

For the reverse containment, let a ∈ ri(A). We will show that T a lies in

ri(T A). By Corollary 16.2.5, ri(T A) is nonempty. So we may pick b ∈ A with T b

in ri(T A). As a ∈ ri(A), there is an ε > 0 so that c = a + ε(a − b) belongs to A.

But a =

1+ε

c +

1+ε

b, so a ∈ [b, c). By linearity, T a lies in [T b, T c). Therefore,

by the Accessibility Lemma (Lemma 16.2.6), T a belongs to ri(T A). ¥

16.2.11. COROLLARY. Suppose that A and B are convex subsets of R

. Then

ri(A + B) = ri(A) + ri(B) and ri(A − B) = ri(A) − ri(B).

568 Convexity and Optimization

PROOF. For the two cases, deﬁne maps T from R

×R

to R

by T (a, b) = a ±b.

Then T (A × B) = A ± B. By the two previous results,

ri(A ± B) = T ri(A × B) = T (ri(A) × ri(B)) = ri(A) ± ri(B).

Exercises for Section 16.2

A. Write out a careful proof of Proposition 16.2.9.

B. Explain why the notion of relative closure of a convex set isn’t needed.

C. Let C be a convex subset of R

and let U be an open set that intersects C. Show that

U ∩ ri(C) is nonempty.

D. Suppose that a convex subset A of R

intersects every (afﬁne) line in a closed interval.

Show that A is closed. HINT: Connect b ∈

A to a in ri(A).

E. Let A be a convex subset of R

that is dense in aff(A). Prove that A = aff(A).

F. Let A be a convex subset of R

. Show that if B is a compact subset of ri(A), then

conv(B) is a compact convex subset of ri(A). HINT: Corollary 16.1.9

G. (a) Show that if A and B are closed convex sets and A is compact, then A + B is a

closed convex set.

(b) If B is also compact, show that A + B is compact.

HINT: Look for two closed convex subsets of R

that lie strictly above the x-axis

but 0 is a limit point of A + B.

H. Suppose that C and D are convex subsets of R

and that C ⊂ D. Show that if

ri(D) ∩ C is nonempty, then ri(C) ⊂ ri(D).

HINT: If d ∈ ri(D) ∩ C and c ∈ ri(C), extend [d, c] beyond c.

I. Suppose that A and B are convex subsets of R

with ri(A) ∩ ri(B) 6= ∅.

(a) Show that A ∩ B = A ∩ B. HINT: Connect b ∈ A ∩ B to a ∈ ri(A) ∩ ri(B).

(b) Show that ri(A ∩ B) = ri(A) ∩ ri(B).

16.3. Separation Theorems

The goal of this section is show that we can separate two disjoint convex sets

from one another by a hyperplane. Geometrically, it seems obvious that, given a

convex set A ⊂ R

and b /∈ A, there is a line that separates b from A. The appro-

priate generalization (replacing the line with a hyperplane) is true in R

. Indeed,

there is a general form of this theorem, called the Hahn–Banach theorem, which

holds for any normed vector space. We prove this result for R

, where we can use

the Heine–Borel Theorem (Theorem 4.4.6).

We start by showing that a convex set in R

always has a unique closest point

to a given point outside. The existence of such a point comes from Exercise 5.4.J

for any closed set and does not require convexity. In convexity theory, the map to

16.3 Separation Theorems 569

this closest point is called a projection, which differs from the meaning of the term

in linear algebra.

16.3.1. CONVEX PROJECTION THEOREM.

Let A be a nonempty closed convex subset of R

. For each point x ∈ R

, there is

a unique point P

(x) in A which is closest to x. The point P

(x) is characterized



x − P

(x), a − P

(x)

≤ 0 for all a ∈ A.

Moreover, kP

(x) − P

(y)k ≤ kx − yk for all x, y ∈ R

Geometrically, the equation says that the line segment [x, P

(x)] makes an

obtuse angle with [a, P

(x)] for every point a ∈ A. The last estimate shows that

has Lipschitz constant 1 and, in particular, is continuous.

PROOF. Pick any vector a

in A, and let R = kx − a

k. Then

0 ≤ inf{kx − ak : a ∈ A} ≤ R.

The closest point to x in A must belong to A∩B

(x). This is the intersection of two

closed convex sets, and so is closed and convex. Moreover, A ∩B

(x) is bounded

and thus compact by the Heine–Borel Theorem (Theorem 4.4.6). Consider the

continuous function on A ∩ B

(x) given by f(a) = kx − ak. By the Extreme

Value Theorem (Theorem 5.4.4), there is a point a

∈ A at which f takes its

minimum—a closest point.

To see that a

is unique, we need to use convexity. Suppose that there is another

vector a

∈ A with kx − a

k = kx − a

k. We will show that b =

+ a

) is

closer, contradicting the choice of a

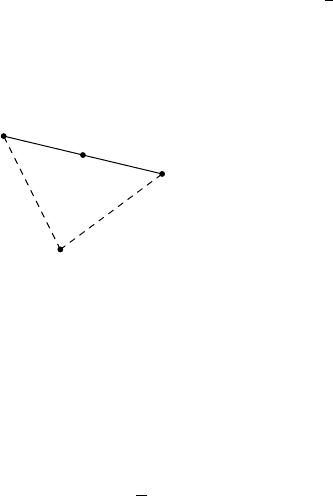
as a closest point. See Figure 16.2. One way

to accomplish this is to apply the parallelogram law (see Exercise 16.3.A). Instead,

we give an elementary argument using Euclidean geometry.

FIGURE 16.2. The points x, a

, a

, and b.

Consider the triangle with vertices x, a

, and a

. As kx − a

k = kx − a

this triangle is isosceles. As kb − a

k = kb − a

k, the point b is the foot of the

perpendicular dropped from x to [a

, a

] and therefore kx−bk < kx−a

k. Indeed,

∠xba

is a right angle, and the Pythagorean Theorem shows that

kx − a

= kx − bk

− a

570 Convexity and Optimization

It now makes sense to deﬁne the function P

by setting it to be this unique

closest point to x. Let a 6= P

(x) be any other point in A. Then for 0 < λ ≤ 1,

kx − a

< kx − (λa + (1 − λ)a

= k(x − a

) − λ(a − a

= kx − a

− 2λhx − a

, a − a

i + λ

ka − a

so that hx−a

, a−a

i ≤

ka−a

. Let λ tend to 0 to obtain hx−a

, a−a

i ≤ 0.

This argument is reversible. If a

is any point such that hx − a

, a − a

i ≤ 0

for all a ∈ A, then

kx − ak

= kx − a

− 2hx − a

, a − a

i + ka − a

≥ kx − a

+ ka − a

Hence a

= P

(x) is the unique closest point.

Let x and y be points in R

. Apply the inequality once for each of x and y:



x − P

(x), P

(y) − P

(x)

≤ 0

and



(y) − y, P

(y) − P

(x)



y − P

(y), P

(x) − P

(y)

≤ 0.

Adding yields h(x − y) + (P

(y) − P

(x)), P

(y) − P

(x)i ≤ 0. Hence

(y) − P

(x)k

≤



y − x, P

(y) − P

(x)

≤ ky − xkkP

(y) − P

(x)k

by the Schwarz inequality (4.1.1). Therefore, kP

(y) − P

(x)k ≤ kx − yk. ¥

16.3.2. EXAMPLE. Let A be the triangle in R

with vertices (0, 0), (1, 0), and

(0, 1) as in Figure 16.3. Then

((x, y)) =











(x, y) if (x, y) ∈ A

(x, 0) if 0 ≤ x ≤ 1 and y ≤ 0

(0, y) if 0 ≤ y ≤ 1 and x ≤ 0

(0, 0) if x ≤ 0 and y ≤ 0

(1, 0) if x ≥ 1 and y ≤ 0

(1, 0) if 0 ≤ y ≤ x − 1

(0, 1) if y ≥ 1 and x ≤ 0

(0, 1) if 0 ≤ x ≤ y − 1

(s, 1 − s) if x + y ≥ 1 and |y − x| ≤ 1, where s =

y+1−x

We can now prove the promised separation theorem, which will be fundamental

to all of our later work. We provide only two consequences in this section. There

are many more.

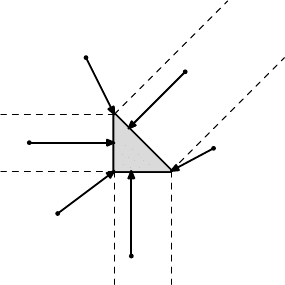
16.3 Separation Theorems 571

FIGURE 16.3. The triangle A and action of P

16.3.3. SEPARATION THEOREM.

Suppose that A is a closed convex set in R

and b /∈ A. Then there is a vector

h ∈ R

and scalar α ∈ R so that ha, hi ≤ α for all a ∈ A but hb, hi > α. In

particular, h determines a hyperplane H so that A is contained in H

−

and b is

contained in the interior of H

PROOF. Let a

= P

(b). As b /∈ A, h = b − a

is a nonzero vector. Deﬁne

α = ha

, hi, and let H = {x : hx, hi = α}. By Theorem 16.3.1, if a ∈ A,

then hb − a

, a − a

i ≤ 0. Rewriting this, we obtain ha, hi ≤ ha

, hi = α.

Therefore, A is contained in H

−

= {x ∈ R

: hx, hi ≤ α}. On the other hand,

hb − a

, b − a

i = khk

> 0, which implies that hb, hi > ha

, hi = α. ¥

16.3.4. COROLLARY. Let A be a closed convex subset of R

. Then b belongs

to A if and only if hb, xi ≤ sup{ha, xi : a ∈ A} for all x ∈ R

PROOF. If b ∈ A, then the inequality is immediate. For the other direction, suppose

that b /∈ A. Take x to be the vector h given by the Separation Theorem,

hb, hi > α ≥ ha, hi for all a ∈ A.

Thus sup{ha, xi : a ∈ A} ≤ α < hb, hi. Therefore, the inequality of the corollary

is valid precisely for b ∈ A. ¥

This corollary has a beautiful geometric meaning. The proof is left as Exer-

cise 16.3.E.

16.3.5. COROLLARY. A closed convex set in R

is the intersection of all the

closed half-spaces that contain it.

572 Convexity and Optimization

16.3.6. DEFINITION. Let A be a closed convex subset of R

and b ∈ rbd(A).

A supporting hyperplane to A at b is a hyperplane H so that b ∈ H and A is

contained in one of the closed half-spaces determined by H.

If aff(A) is a proper subspace of R

, then it is contained in a hyperplane that

supports A. We regard this as a pathological situation and call H a nontrivial

supporting hyperplane if it does not contain aff(A).

16.3.7. SUPPORT THEOREM.

Let A be a convex subset of R

and b ∈ rbd(A). Then there is a nontrivial sup-

porting hyperplane to A at b.

PROOF. We may suppose that A is closed by replacing A with

A. Let a

be any

point in ri(A). By the Accessibility Lemma (Lemma 16.2.6), the interval [a

, b) is

contained in ri(A). By the same token, the point b

:= b +

(b − a

) is not in A

for k ≥ 1, as that would put b into ri(A). Let h

= (b

−P

)/kb

−P

k. The

proof of the Separation Theorem (Theorem 16.3.3) shows that

ha, h

i ≤ α

:= hP

, h

i < hb

, h

i for all a ∈ A.

By the Heine–Borel Theorem (Theorem 4.4.6), the unit sphere of R

is com-

pact. Thus the sequence {h

: k ≥ 1} has a convergent subsequence (h

)

∞

i=1

with

limit h = lim

i→∞

. Then since P

is continuous,

lim

i→∞

= lim

i→∞

, h

i = hP

b, hi = hb, hi =: α.

If a ∈ A, then

ha, hi = lim

i→∞

ha, h

i ≤ lim

i→∞

= α.

So A is contained in the half-space H

−

= {x : hx, hi ≤ α}.

The vectors h

all lie in the subspace L(A), and thus so does h. Consequently,

b + h belongs to aff(A). Since hb + h, hi = α + 1 > α, it follows that H does not

contain aff(A). So H is a nontrivial supporting hyperplane. ¥

Exercises for Section 16.3

A. Use the parallelogram law (Exercise 7.4.A) to give a different proof of the uniqueness

portion of Theorem 16.3.1.

B. Let A =

(a). Find an explicit formula for P

(x).

C. If A = B

(a) and b ∈ rbd(A), show that the unique supporting hyperplane to A at b

is H = {x : hx − a, b − ai = r

D. Let A be a subspace. Show that P

(x) is the (linear) orthogonal projection onto A.

E. Show that a closed convex set in R

is the intersection of all the closed half-spaces

that contain it.

F. Let A ⊂ R

be a nonempty open convex set. Show that a ∈ A if and only if for each

hyperplane H of R

containing a, the two open half-spaces int H

and intH

−

both

contain elements of A.