Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


15.3 Multiresolution Analysis 523
We now are ready to derive the infinite decomposition.
15.3.5. THEOREM. Suppose that V
k
⊂ V
k+1
for k ∈ Z is the nested sequence
of subspaces from a multiresolution of L
2
(R). Then L
2
(R) decomposes as the
infinite direct sum
L
k∈Z
W
k
.
PROOF. The finite decompositions are valid. So, in particular,
V
n
= V
−n
⊕ W
−n
⊕ ··· ⊕ W
n−1
.
Thus if f belongs to V
n
and is orthogonal to V
−n
, then f decomposes uniquely as
f =
n−1
P
k=−n
f
k
for f
k
∈ W
k
, namely f
k
= Q
k
f. Moreover, Parseval’s Theorem
shows that kf k
2
2
=
n−1
P
k=−n
kf
k
k
2
2
.
If f is an arbitrary function in L
2
(R) and ε > 0, then by the lemma we may
choose a positive integer n so that k(I − P
n
)fk
2
2
+ kP
−n
fk
2
2
< ε
2
. Therefore,
g
n
:= P
n
f − P
−n
f belongs to V
n
and is orthogonal to V
−n
. Consequently, we
may write g
n
=
n−1
P
k=−n
f
k
for f
k
∈ W
k
, where f
k
= Q
k
g
n
= Q
k
f. By Parseval’s
Theorem,
kf − g
n
k
2
2
= k(I − P
n
)f + P
−n
fk
2
2
= k(I − P
n
)fk
2
2
+ kP
−n
fk
2
2
< ε
2
.
Since ε is arbitrary, it follows that g
n
converges to f . That is,
f = lim
n→∞
n−1
X
k=−n
f
k
=
∞
X
k=−∞
f
k
and
kfk
2
2
= lim
n→∞
kg
n
k
2
2
= lim
n→∞
n−1
X
k=−n
kf
k
k
2
2
=
∞
X
k=−∞
kf
k
k
2
2
.
To establish uniqueness, suppose that f =
P
k
f
k
=
P
k
h
k
are two decom-
positions with f
k
and h
k
in W
k
. Then 0 =
P
k
f
k
− h
k
. The norm formula from
the previous paragraph shows that 0 =
P
k
kf
k
− h
k
k
2
2
. Therefore, h
k
= f
k
for all
k ∈ Z. ¥
Exercises for Section 15.3
A. Let V
0
be the span of integer translates of the Haar scaling function ϕ. Suppose that
f ∈ V
0
has bounded support and the set {f(x −j) : j ∈ Z} is orthonormal. Prove that
f(x) = ±ϕ(x − n) for some integer n.
HINT: Compute hf (x), f(x − j)i when the supports overlap on a single interval.
B. Suppose that ϕ ∈ L
2
(R) such that the subspaces V
k
satisfy orthogonality, nesting, and
scaling. Let M =
S
k∈Z
V
k
. Show that if f ∈ M , then f(x −t) ∈ M for every t ∈ R.
HINT: First prove this for t = j2
−k
. Then apply Exercise 15.1.F.
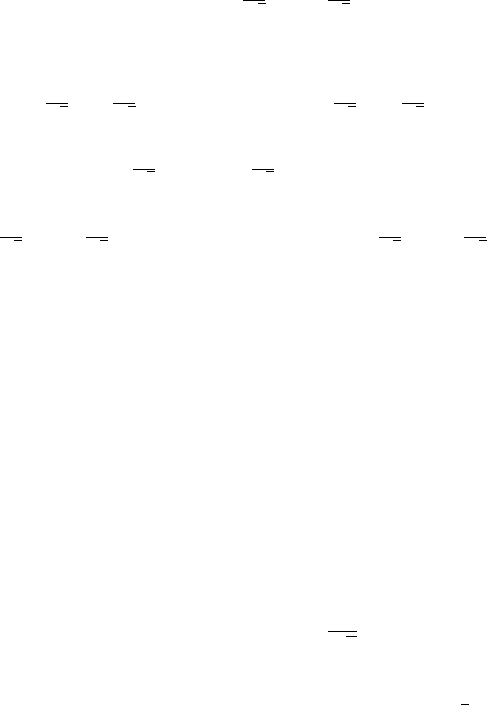
524 Wavelets
C. Suppose that ϕ is continuous with compact support [a, a + M], and that {ϕ
0j
: j ∈ Z}
are orthonormal.
(a) Suppose that f ∈ V
k
, and express f(x) =
P
j
c
j
2
k/2
ϕ(2
k
x−j). Use the Cauchy–
Schwarz inequality to show that |f (x)| ≤ 2
k/2
Mkϕk
∞
kfk
2
.
(b) Show that
T
k∈Z
V
k
= {0}.
HINT: Let f ∈
T
k∈Z
V
k
. Use part (a) to estimate
R
N
−N
|f(x)|
2
dx, and let N → −∞.
15.4. Recovering the Wavelet
Let us look at the decomposition obtained in the previous section in the case of
the Haar system. Notice that ϕ =
χ
[0,1)
satisfies the identity
ϕ =
χ
[0,.5)
+
χ
[.5,1)
=
1
√
2
ϕ
10
+
1
√
2
ϕ
11
.
On the other hand, we can write ϕ
10
and ϕ
11
in terms of ϕ and ψ. Recalling that
ψ =
χ
[0,.5)
−
χ
[.5,1)
, we have
ϕ
10
=
1
√
2
ϕ +
1
√
2
ψ and ϕ
11
=
1
√
2
ϕ −
1
√
2
ψ.
More generally,
ϕ
kj
=
1
√
2
ϕ
k+1,2j
+
1
√
2
ϕ
k+1,2j+1
and
ϕ
k+1,2j
=
1
√
2
ϕ
kj
+
1
√
2
ψ
kj
and ϕ
k+1,2j+1
=
1
√
2
ϕ
kj
−
1
√
2
ψ
kj
.
The subspace V
k
consists of those L
2
(R) functions that are constant on the
dyadic intervals of length 2
−k
. Now ψ
kj
belongs to V
k+1
, it is supported on one
interval of length 2
−k
, and integrates to 0. Thus hψ
kj
, ϕ
kj
0
i = 0 for all j, j
0
∈ Z.
In particular, ψ
kj
lies in W
k
. So W
0
k
= span{ψ
kj
: j ∈ Z} is a subspace of W
k
.
On the other hand, the identities show that every basis vector ϕ
k+1,j
belongs
to V
k
+ W
0
k
, and thus V
k+1
= V
k
⊕ W
0
k
= V
k
⊕ W
k
. This forces the identity
W
0
k
= W
k
. So we have shown that for the Haar system, we have
W
k
= span{ψ
kj
: j ∈ Z}.
There is a systematic way to construct a wavelet from a multiresolution. That is
the goal of this section. Let {V
k
} be a multiresolution with scaling function ϕ. The
construction begins with the fact that ϕ ∈ V
0
⊂ V
1
. Since ϕ
1j
form an orthonormal
basis for V
1
, we may expand ϕ as
ϕ(x) =
∞
X
j=−∞
a
j
ϕ(2x − j) =
∞
X
j=−∞
a
j
√
2
ϕ
1j
(x),(15.4.1)
where a
j
= 2hϕ(x), ϕ(2x − j)i. By Parseval’s Theorem, kϕk
2
2
=
1
2
∞
P
j=−∞
|a
j
|
2
.
Thus (a
j
) is a sequence in `
2
. Equation (15.4.1) is known as the scaling relation
for ϕ.

15.4 Recovering the Wavelet 525
15.4.2. THEOREM. Let ϕ be the scaling function generating a multiresolution
{V
k
} of L
2
(R) with scaling relation ϕ(x) =
∞
P
j=−∞
a
j
ϕ(2x − j). Define
ψ(x) =
∞
X
j=−∞
(−1)
j
a
1−j
ϕ(2x − j).
Then ψ is a wavelet generating the wavelet basis {ψ
kj
: k, j ∈ Z} such that
W
k
= span{ψ
kj
: j ∈ Z} for each k ∈ Z.
PROOF. Since this proof basically consists of several long computations, we pro-
vide a brief overview of the plan. The orthonormality of {ϕ(x − j) : j ∈ Z} will
yield conditions on the coefficients a
j
. Then we show that {ψ(x − k) : k ∈ Z} is
an orthonormal set that is orthogonal to the ϕ(x − j)’s. Finally, we show that V
1
is
spanned by V
0
and the ψ(x − k)’s.
In this proof, all summations are from −∞ to +∞, but for notational simplic-
ity, only the index will be indicated. We define δ
0n
to be 1 if n = 0 and 0 otherwise.
To begin, we have
δ
0n
=
ϕ(x), ϕ(x − n)
®
=
D
X
i
a
i
ϕ(2x − i),
X
j
a
j
ϕ(2x − 2n − j)
E
=
X
i
X
j
a
i
a
j
ϕ(2x − i), ϕ(2x − 2n − j)
®
=
1
2
X
j
a
j+2n
a
j
.
The orthonormality of {ψ(x−j) : j ∈ Z}follows because the coefficients of ψ
are obtained from ϕ by reversing, shifting by one place, and alternating sign. A bit
of thought will show that each of these steps preserves the property of orthogonality
of translations. Here we provide the direct computation:
ψ(x), ψ(x−n)
®
=
D
X
i
(−1)
i
a
1−i
ϕ(2x−i),
X
j
(−1)
j
a
1−j
ϕ(2x−2n−j)
E
=
X
i
X
j
(−1)
i+j
a
1−i
a
1−j
ϕ(2x − i), ϕ(2x−2n−j)
®
=
1
2
X
j
(−1)
2j+2n
a
1−j−2n
a
1−j
=
1
2
X
i
a
i
a
i+2n
= δ
0n
.
So {ψ(x − j) : j ∈ Z} is orthonormal.
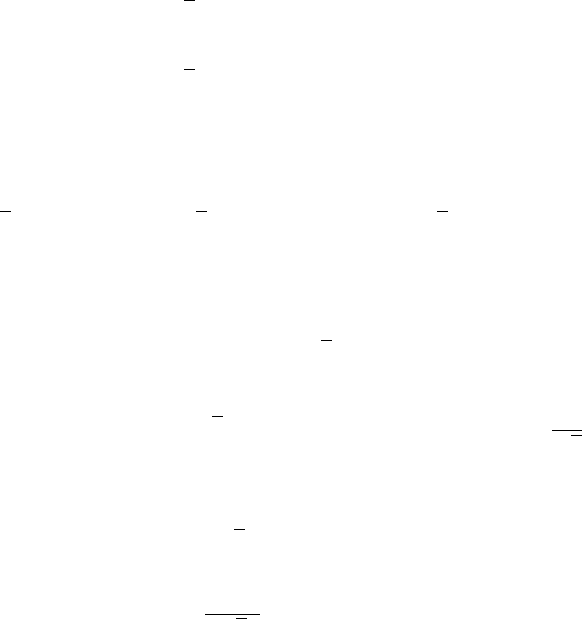
526 Wavelets
The fact that the ψ’s and ϕ’s are orthogonal is more subtle. Calculate
ψ(x−m), ϕ(x−n)
®
=
D
X
i
(−1)
i
a
1−i
ϕ(2x−2m−i),
X
j
a
j
ϕ(2x−2n−j)
E
=
X
i
X
j
(−1)
i
a
1−i
a
j
ϕ(2x−2m−i), ϕ(2x−2n−j)
®
but the inner product is 0 unless 2m + i = 2n + j,
=
1
2
X
j
(−1)
j+2n−2m
a
1−j−2n+2m
a
j
=
1
2
X
j
(−1)
j
a
p−j
a
j
,
where p = 2m + 1 − 2n is a fixed odd integer. Thus by substituting i = p − j, we
may rearrange this sum:
1
2
X
j
(−1)
j
a
p−j
a
j
=
1
2
X
i
(−1)
p−i
a
i
a
p−i
= −
³
1
2
X
i
(−1)
i
a
i
a
p−i
´
.
Thus the sum must be 0. Hence the family {ψ(x − k) : k ∈ Z} is orthogonal to
the family {ϕ(x − j) : j ∈ Z}. Notice that the shift by 1 of the coefficients in the
definition of ψ was to make p odd in this calculation.
Now we wish to express ϕ
1p
(x) =
√
2ϕ(2x − p) as a linear combination of
these two families. To see what the coefficients should be, we compute
ϕ
1p
(x), ϕ(x − n)
®
=
D
√
2ϕ(2x − p),
X
j
a
j
ϕ(2x−2n−j)
E
=
1
√
2
a
p−2n
since the inner product is 0 except when 2n + j = p; and similarly
ϕ
1p
(x), ψ(x − n)
®
=
D
√
2ϕ(2x − p),
X
j
(−1)
j
a
1−j
ϕ(2x−2n−j)
E
=
(−1)
p
√
2
a
1−p+2n
.
So now it is a matter of adding up the series to see if ϕ
1p
(x) can be recovered.
Compute
X
n
a
p−2n
ϕ(x − n) =
X
n
X
i
a
p−2n
a
i
ϕ(2x−2n−i)
=
X
k
³
X
n
a
p−2n
a
k−2n
´
ϕ(2x − k)
=
X
k
³
X
n
a
p+2n
a
k+2n
´
ϕ(2x − k)
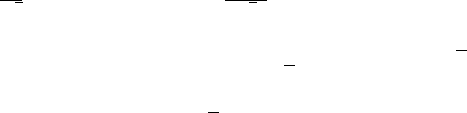
15.4 Recovering the Wavelet 527
and
X
n
(−1)
p
a
1−p+2n
ψ(x − n) =
X
n
X
i
(−1)
p
a
1−p+2n
(−1)
i
a
1−i
ϕ(2x−2n−i)
=
X
k
³
(−1)
p+k
X
n
a
1+2n−p
a
1+2n−k
´
ϕ(2x − k).
When p + k is odd,
(−1)
p+k
X
n
a
1+2n−p
a
1+2n−k
= −
X
m
a
2m+k
a
2m+p
while if p + k is even,
(−1)
p+k
X
n
a
1+2n−p
a
1+2n−k
=
X
m
a
1+2m+k
a
1+2m+p
.
When these sums over translates of ϕ(2x) and ψ(2x) are added together, the
coefficients of ϕ(2x −k) are canceled when p + k is odd, while for p + k even the
two sums conveniently merge to yield the sums from the orthogonality relation for
the ϕ(x − k). Hence the sum obtained is
X
n
1
√
2
a
p−2n
ϕ(x − n) +
X
n
(−1)
p
√
2
a
1−p+2n
ψ(x − n)
=
X
k≡p mod 2
³
1
2
X
n
a
p+n
a
k+n
´
√
2ϕ(2x − k)
=
√
2ϕ(2x − p) = ϕ
1p
(x).
Set W = span{ψ(x − j) : j ∈ Z}. Let us recap what we have established.
We have shown that {ψ(x − j) : j ∈ Z} is an orthonormal basis for W , that W is
orthogonal to V
0
, and that ϕ(2x − i) belongs to V
0
+ W for all i ∈ Z. Since each
ψ(x − j) is expressed in terms of the ϕ(2x − i), it is clear that W is a subspace
of V
1
. On the other hand, since each ϕ(2x − i) belongs to V
0
+ W , it follows that
V
1
= V
0
⊕W . Hence we deduce that W is the orthogonal complement of V
0
in V
1
;
that is, W = W
0
.
It now follows from dilation that
span{ψ
kj
: j ∈ Z} = {2
k/2
f(2
k
x) : f ∈ W
0
} = W
k
.
Hence {ψ
kj
: j ∈ Z} is an orthonormal basis for W
k
for each k ∈ Z. Since
L
2
(R) =
L
+∞
k=−∞
W
k
, it follows that together the collection {ψ
kj
: k, j ∈ Z} is
an orthonormal basis for L
2
(R). Therefore, ψ is a wavelet. ¥
Exercises for Section 15.4
A. Show that if ϕ is a scaling function with compact support, then the scaling relation is
a finite sum.
B. Let {e
k
: k ∈ Z} be an orthonormal set in a Hilbert space H. Show that the vectors
x =
P
n
a
n
e
n
and y =
P
n
(−1)
n
a
p−n
e
n
are orthogonal if p is odd.
528 Wavelets
C. Given the scaling relation ϕ(x) =
P
j
a
j
ϕ(2x − j), we define the filter to be the
complex function m
ϕ
(θ) =
P
j
a
j
e
ijθ
. Prove that |m
ϕ
(θ)|
2
+ |m
ϕ
(θ + π)|
2
= 1.
HINT: Compute the Fourier series of this sum, and compare the sums of coefficients
obtained with those that occur in the proof of Theorem 15.4.2.
D. Suppose that ϕ is a scaling function that is bounded, has compact support, and satisfies
R
∞
−∞
ϕ(x) dx 6= 0. Let ϕ(x) =
P
j
a
j
ϕ(2x − j) be the scaling relation.
(a) Show that
P
j
a
j
= 2. HINT: Integrate over R.
(b) Show that
P
j
(−1)
j
a
j
= 0. HINT: Use the previous exercise for θ = 0.
15.5. Daubechies Wavelets
The multiresolution analysis developed in the last two sections can be used to
design a continuous wavelet. We start by explaining the properties we want. The
only example we have so far of a wavelet system and multiresolution analysis is
the Haar wavelet system. The Haar wavelet ψ satisfies
Z
ψ(x) dx = 0
and the multiresolution analysis uses subspaces of functions that are constant on
dyadic intervals of length 2
k
, k ∈ Z. As a result, Haar wavelets do a good job of
approximating functions that are locally constant.
It is possible to do a better job of approximating continuous functions if we use
a wavelet that also satisfies
Z
xψ(x) dx = 0.
If you computed moments of inertia in calculus, you won’t be surprised to learn
that this is called the first moment of ψ.
Our goal in this section is to construct a continuous wavelet with this property.
To be honest, our construction is not quite complete. At one crucial point, we
will assume the uniform convergence of a sequence of functions to a continuous
function. The full construction of this wavelet requires considerable work, although
in the next section we provide a proof that the sequence converges in L
2
. Later in
this chapter, we give a full proof of the existence of another continuous wavelet,
known as the Franklin wavelet.
This is part of a general family of wavelets constructed by Ingrid Daubechies
in 1988. Hence these wavelets are called Daubechies wavelets.
15.5.1. THEOREM. There is a continuous function ϕ of compact support in
L
2
(R) that generates a multiresolution of L
2
(R) so that the associated wavelet ψ
is continuous, has compact support, and satisfies
R
ψ(x) dx =
R
xψ(x) dx = 0.
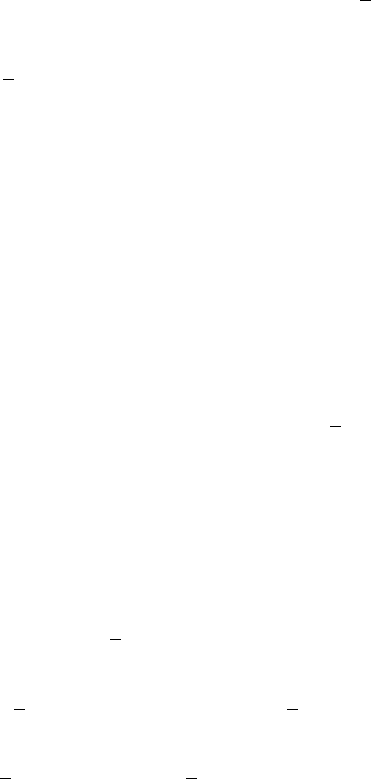
15.5 Daubechies Wavelets 529
PROOF. As in the last section, all of our summations are from −∞ to +∞; so only
the index is given. We will look for a function ϕ with norm 1 and integral 1, that is,
kϕk
2
2
=
Z
+∞
−∞
|ϕ(x)|
2
dx = 1 and
Z
+∞
−∞
ϕ(x) dx = 1.
Beyond these normalizing assumptions, we use the crucial idea of the previous
section by assuming that ϕ satisfies a scaling relation ϕ(x) =
P
j
a
j
ϕ(2x − j).
Since we wish ϕ to have compact support, this must be a finite sum.
Compute what follows from our assumptions:
1 = kϕk
2
2
=
Z
+∞
−∞
|ϕ(x)|
2
dx =
Z
+∞
−∞
¯
¯
¯
X
j
a
j
ϕ(2x − j)
¯
¯
¯
2
dx
=
D
X
j
a
j
ϕ(2x − j),
X
k
a
k
ϕ(2x − k)
E
=
1
2
X
j
|a
j
|
2
,
where we use the fact that {ϕ(2x − j) : j ∈ Z} is an orthogonal set of vectors in
L
2
(R) with norm 1/
√
2. In the same way,
R
ϕ(x) dx = 1 implies that
P
j
a
j
= 2.
From Theorem 15.4.2, if we can find a suitable sequence (a
k
), then there is a
wavelet ψ, also of norm 1, which is given by
(15.5.2) ψ(x) =
X
j
(−1)
j
a
1−j
ϕ(2x − j).
Consider the consequences of the integral conditions on ψ, namely
R
ψ(x) dx = 0
and
R
xψ(x) dx = 0, to obtain two more relations that the sequence (a
n
) must
satisfy.
0 =
Z
ψ(x) dx =
Z
X
j
(−1)
j
a
1−j
ϕ(2x − j) dx
=
X
j
(−1)
j
a
1−j
Z
ϕ(2x − j) dx =
1
2
X
j
(−1)
j
a
1−j
Replace 1−j with j and use (−1)
1−j
= −(−1)
j
to obtain
P
j
(−1)
j
a
j
= 0.
Similarly,
0 =
Z
xψ(x) dx =
X
j
(−1)
j
a
1−j
Z
xϕ(2x − j) dx
=
X
j
(−1)
j
a
1−j
1
4
Z
(t + j)ϕ(t) dt
= −
³
1
4
X
j
(−1)
j
a
1−j
´
Z
tϕ(t) dt −
³
1
4
X
j
(−1)
j
ja
1−j
´
Z
ϕ(t) dt
= −
1
4
X
j
(−1)
j
ja
1−j
=
1
4
X
k
(−1)
k
(1 − k)a
k
530 Wavelets
=
1
4
X
k
(−1)
k
a
k
−
1
4
X
k
(−1)
k
ka
k
= −
1
4
X
k
(−1)
k
ka
k
.
Summarizing, we have the following equations:
X
j
|a
j
|
2
=
X
j
a
j
= 2 and
X
j
(−1)
j
a
j
=
X
j
(−1)
j
ja
j
= 0.
As you can verify directly, one solution to these equations is given by
a
0
=
1 +
√
3
4
, a
1
=
3 +
√
3
4
, a
2
=
3 −
√
3
4
, a
3
=
1 −
√
3
4
with a
j
= 0 for all other j ∈ Z.
Substituting these values back into the scaling relation, we want the scaling
function to satisfy
ϕ(x) =
1+
√
3
4
ϕ(2x)+
3+
√
3
4
ϕ(2x−1)+
3−
√
3
4
ϕ(2x−2)+
1−
√
3
4
ϕ(2x−3)
= a
0
ϕ(2x) + a
1
ϕ(2x − 1) + a
2
ϕ(2x − 2) + a
3
ϕ(2x − 3).
It is not immediately clear why there should be a continuous function satisfying
this equation.
We can construct such a function as the limit of a sequence of functions (ϕ
n
),
defined by ϕ
0
=
χ
[0,1)
and for n ≥ 0,
ϕ
n+1
(x) = a
0
ϕ
n
(2x) + a
1
ϕ
n
(2x − 1) + a
2
ϕ
n
(2x − 2) + a
3
ϕ
n
(2x − 3)
From the first few ϕ
n
, graphed in Figure 15.2, it is plausible that the sequence
(ϕ
n
) converges to a continuous function. However, proving this requires careful
arguments using the Fourier transform, and so is beyond the scope of this book.
We content ourselves with stating the following theorem.
15.5.3. THEOREM. The sequence of functions (ϕ
n
) converges uniformly to a
continuous function ϕ.
We will prove convergence in L
2
(R) in the next section. The other properties
of the Daubechies wavelet can now be deduced. Note that except for the continuity
of ϕ and ψ, all of the other properties follow from convergence in L
2
(R).
15.5.4. COROLLARY. The Daubechies wavelet ϕ satisfies the properties:
(1) ϕ(x) = a
0
ϕ(2x) + a
1
ϕ(2x − 1) + a
2
ϕ(2x − 2) + a
3
ϕ(2x − 3).
(2) ϕ is supported on [0, 3].
(3) kϕk
2
= 1 and
R
ϕ(x) dx = 1.
(4) ψ(x) = −a
0
ϕ(2x − 1) + a
1
ϕ(2x) − a
2
ϕ(2x + 1) + a
3
ϕ(2x + 2)
is continuous with support in [−1, 2].
(5)
R
ψ(x) dx =
R
xψ(x) dx = 0.
(6) {ϕ(x − j), ψ(x − j) : j ∈ Z} is orthonormal.
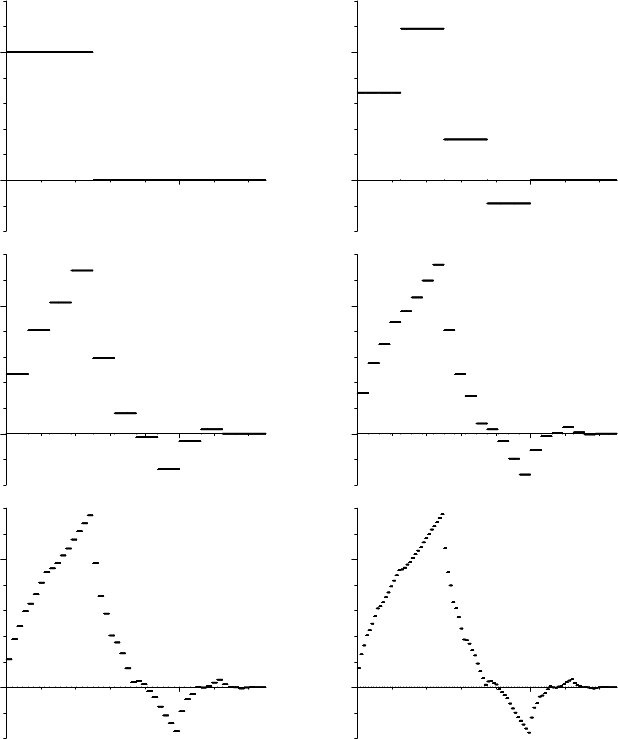
15.5 Daubechies Wavelets 531
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
0
1
2
FIGURE 15.2. The graphs of ϕ
0
through ϕ
5
.
PROOF. The proof will be left as an exercise using the following outline.
From the definition of ϕ
n+1
in terms of ϕ
n
and the convergence to ϕ, it follows
immediately that ϕ satisfies the scaling relation. The Haar function ϕ
0
=
χ
[0,1)
satisfies (2) and (3) and (6a): {ϕ
0
(x − j) : j ∈ Z} is orthonormal. We also
introduce the functions
ψ
n+1
(x) = −a
0
ϕ
n
(2x − 1) + a
1
ϕ
n
(2x) − a
2
ϕ
n
(2x + 1) + a
3
ϕ
n
(2x + 2)
for n ≥ 0. We show by induction that ϕ
n
and ψ
n
satisfy (2)–(6) for all n ≥ 1 with
the exception of continuity for ψ
n
, and thus they hold in the limit. The continuity
of ψ follows from the continuity of ϕ. ¥
At this point, a reasonable objection is that we do not have anything resembling
a formula for the scaling function ϕ, much less the wavelet ψ that goes along with

532 Wavelets
it. The remedy is to observe that the scaling relation provides a way to evaluate ϕ
at points k/2
n
for k, n ∈ Z, n ≥ 0.
Since ϕ is continuous and has support contained in [0, 3], ϕ(i) = 0 for all
integers i other than 1 and 2. Thus,
ϕ(2) = a
0
ϕ(4) + a
1
ϕ(3) + a
2
ϕ(2) + a
3
ϕ(1)
= a
2
ϕ(2) + a
3
ϕ(1).
Similarly, ϕ(1) = a
0
ϕ(2) + a
1
ϕ(1). Solving these equations yields
ϕ(1) = (1 +
√
3)/2 and ϕ(2) = (1 −
√
3)/2.
From the values at the integers, we can now evaluate ϕ at all numbers of the
form k/2 by using the scaling relation. For example,
ϕ
¡
1
2
¢
= a
0
ϕ(1) + a
1
ϕ(0) + a
2
ϕ(−1) + a
3
ϕ(−2) = (2 +
√
3)/4.
Likewise, as the reader should verify, ϕ(3/2) = 0 and ϕ(5/2) = (2 −
√
3)/4.
Continuing in this way, we can then obtain the values of ϕ at points of the form
k/4 (k odd), then at k/8 (k odd), and so on. As ϕ is continuous, the values at the
points k/2
n
for some sufficiently large n will provide a reasonable graph of ϕ, such
as that given in Figure 15.3.
0
1
1
2 3
FIGURE 15.3. The Daubechies scaling function.
Similarly, using the relation (15.5.2), we can find the values of ψ at points k/2
n
and graph ψ; see Figure 15.4.
Exercises for Section 15.5
A. Prove Corollary 15.5.4 following the outline given there.
B. Evaluate the Daubechies wavelet ψ at the points k/4 for k ∈ Z.
C. WhichDaubechies wavelet coefficientsare nonzero for the function givenby f(x) = x
on [0, 2] and 0 elsewhere?
