Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.

14.6 Ces
`
aro Summation of Fourier Series 493
This proof has a strong resemblance to our proof of the Weierstrass Approxi-
mation Theorem. The common underlying technique here is controlling the integral
of a product by splitting the integral into two parts, where one factor of the product
is well-behaved on each part. For another example, look at the proof of one of the
inequalities in Theorem 14.4.3 (3).
In fact, it is possible to prove the Weierstrass Approximation Theorem using
Fej
´
er’s Theorem. One proof is outlined in the Exercises. Another will be given in
Section 14.9.
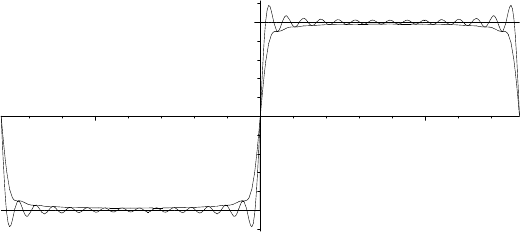
14.6.5. EXAMPLE. Consider the function h introduced in Example 14.4.6,
h(x) =
(
1 for 0 ≤ x ≤ π
−1 for −π < x < 0.
The sequenceS
n
h willexhibit Gibbs’s phenomenon (see Exercise 14.5.A) as shown
in Figure 14.5. We will compute the Ces
`
aro means for this function using the F
´
ejer
kernel. Since h is an odd function, the approximants S
n
h and σ
n
h are also all odd.
Also, h(π − x) = h(x), and so S
n
h and σ
n
h also have this symmetry. Consider a
point x in [0, π/2].
σ
n
h(x) =
Z
π
−π
h(x + t)K
n
(t) dt
= −
Z
−x
−π
K
n
(t) dt +
Z
π−x
−x
K
n
(t) dt −
Z
π
π−x
K
n
(t) dt
=
Z
x
−x
K
n
(t) dt −
Z
π+x
π−x
K
n
(t) dt
Here we have exploited the fact that K
n
is even to cancel the integral from x to
π − x with the integral from x − π to −x.
–1
1
–2 2
FIGURE 14.5. The graphs of h, S
30
h, and σ
30
h on [−π, π].
By Proposition 14.6.3, the first integral converges to 1 for x in (0, π/2]; while
the second term tends to 0. On the other hand, σ
n
h(0) = 0 for any n. Rewrite
σ
n
h(x) as 2
Z
x
0
K
n
(t) − K
n
(π −t) dt. Since K
n
is positive on [0, π], it follows

494 Fourier Series and Approximation
that σ
n
h(x) is monotone increasing on [0, π/2], then decreases symmetrically back
down to 0 at π. Also, 0 < σ
n
h(x) < 1 here because
Z
x
−x
K
n
(t) dt < 1. Likewise,
by symmetry, σ
n
h(x) converges to −1 on (−π, 0) and σ
n
h(−π) = 0 for all n.
From the monotonicity, we can deduce that this convergence is uniform on
intervals [ε, π − ε] ∪ [ε − π, −ε] for ε > 0. Since the function h has jump discon-
tinuities at the points 0 or ±π, continuous functions cannot converge uniformly to
it near these points.
Exercises for Section 14.6
A. Show that if f is an absolutely integrable function with lim
n→∞
S
n
f(θ) = a, then
lim
n→∞
σ
n
f(θ) = a.
B. Show that if f is a piecewise continuous function with a jump discontinuity at θ, then
lim
n→∞
σ
n
f(θ) =
f(θ
+
) + f(θ
−
)
2
.
HINT: Write f as the sum of a continuous function g and a piecewise C
1
function h.
Use Exercise A on h.
C. Show that kσ
n
fk
∞
≤ kfk
∞
.
D. Let
P
j≥0
a
j
be an infinite series. Define s
n
=
n
P
j=0
a
j
and σ
n
=
1
n
n−1
P
j=0
s
j
.
(a) If lim
n→∞
s
n
= L, show that lim
n→∞
σ
n
= L.
(b) Show by example that the converse of (a) is false.
(c) Hardy’s Tauberian Theorem: Show that if lim
n→∞
na
n
= 0 and lim
n→∞
σ
n
= L, then
lim
n→∞
s
n
= L. HINT: Verify that s
N
− σ
N+1
=
1
N+1
N
P
j=1
ja
j
.
E. Suppose that f is a 2π-periodic function and that |A
n
| + |B
n
| ≤ C/n for n ≥ 1 and
some constant C.
(a) Find a bound for S
n
f(θ) − σ
n
f(θ) =
n
P
k=1
k
n + 1
A
k
coskθ +
k
n + 1
B
k
sinkθ.
Hence show that kS
n
fk
∞
≤ kfk
∞
+ C.
(b) Apply this to obtain a uniform bound for S
n
f for the function f used in our exam-
ple of Gibbs’s phenomenon.
F. Prove Weierstrass’s Approximation Theorem for a continuous function f on [0, π] as
follows:
(a) Set g(θ) = f(|θ|) for θ ∈ [−π, π]. This is an even, continuous, 2π-periodic func-
tion. Use Fej
´
er’s Theorem to approximate g within ε/2 by a trig polynomial.
(b) Use the fact that the Taylor polynomials for cosnθ converge uniformly on [0, π] to
approximate the trigonometric polynomial by actual polynomials within ε/2.

14.7 Best Approximation by Trig Polynomials 495
14.7. Best Approximation by Trig Polynomials
We return to the theme of Chapter 10, uniform approximation. Here we are
interested in approximating 2π-periodic functions by (finite) linear combinations
of trigonometric functions. In this section, we obtain some reasonable estimates.
Later we will establish the Jackson and Bernstein Theorems, which yield optimal
estimates. It will turn out that there are close connections with approximation by
polynomials which we also explore.
The degree of a trigonometric polynomial q(x) = a
0
+
P
n
k=1
a
k
coskx +
b
k
sinkx is n if |a
n
|+ |b
n
| > 0 and a
k
= b
k
= 0 for all k > n. We let TP
n
denote
the subspace of C[−π, π] consisting of all trigonometric polynomials of degree at
most n.
14.7.1. DEFINITION. The error of approximation to a 2π-periodic function
f by trigonometric polynomials of degree n is
e
E
n
(f) = inf{kf − qk
∞
: q ∈ TP
n
}
For example, for any 2π-periodic function f ∈ C[−π, π], both S
n
f and σ
n
f
are in TP
n
. The subspace TP
n
has dimension 2n + 1 because it is spanned by the
linearly independent functions {1, coskx, sinkx : 1 ≤ k ≤ n}. It follows from the
compactness argument of Theorem 7.6.5 that there is a best approximation in TP
n
to any function f. That is, given f in C[−π, π], there is a trig polynomial p in TP
n
so that
kf − pk
∞
= inf{kf − qk
∞
: q ∈ TP
n
} =
e
E
n
(f).
In a certain sense, the functions S
n
f and σ
n
f are natural approximants to f
in TP
n
. Theorem 14.1.2 shows that S
n
f is the best L
2
norm approximant to f in
TP
n
. However, it has some undesirable wildness when it comes to the uniform
norm. F
´
ejer’s Theorem (Theorem 14.6.4) suggests that σ
n
f is a reasonably good
approximant in the uniform norm. The following theorem gives bounds on how
close S
n
f is to the best approximation in TP
n
. It says that S
n
f can be a relatively
bad approximation for large n. Nevertheless, the degree of approximation by S
n
f
is sufficiently good to yield reasonable approximations if the Fourier series decays
at a sufficient rate.
On the other hand, while σ
n
f is in general a superior approximant, consider
f(x) = sin nx. Then S
n
f = f is the best approximation with
e
E
n
(f) = 0, while
σ
n
f(x) =
1
n+1
sinnx is a rather poor estimate. In spite of this, good general results
can be obtained from the obvious estimate
e
E
n
(f) ≤ kf − σ
n
fk
∞
.
The reason that S
n
works in the following theorem is the fact that S
n
p = p for all
p in TP
n
.
14.7.2. THEOREM. If f : R → R is a continuous 2π-periodic function, then
kf − S
n
fk
∞
≤ (3 + log n)
e
E
n
(f).

496 Fourier Series and Approximation
PROOF. By Theorem 14.4.2,
S
n
f(x) =
Z
π
−π
f(x + t)D
n
(t) dt.
Hence by Theorem 14.4.3 (3), we have
kS
n
fk
∞
≤ kf k
∞
Z
π
−π
¯
¯
D
n
(t)
¯
¯
dt ≤ (2 + logn)kfk
∞
.
Observe that if p ∈ TP
n
, then S
n
p = p. In particular, if we let p ∈ TP
n
be the best
approximation to f, then
kf − S
n
fk
∞
≤ k(f − p) − S
n
(f − p)k
∞
≤ kf − pk
∞
+ kS
n
(f − p)k
∞
≤ kf − pk
∞
+ (2 + log n)kf − pk
∞
≤ (3 + log n)kf − pk
∞
.
As kf − pk
∞
=
e
E
n
(f) for our choice of p, we obtain the desired estimate. ¥
We can now apply this estimate to show that the Dirichlet–Jordan Theorem
actually yields uniform convergence when the piecewise Lipschitz function is con-
tinuous.
14.7.3. THEOREM. If f is a 2π-periodic Lipschitz function with Lipschitz con-
stant L, then for n ≥ 2
kf − σ
n
fk
∞
≤
(1 + 2 log n)L
2n
.
Consequently,
kf − S
n
fk
∞
≤
2π(1 + logn)
2
L
n
.
In particular, S
n
f converges to f uniformly on [−π, π].
PROOF. We need a decent estimate for the F
´
ejer kernel. For our purposes, the
following is enough:
K
n
(t) =
1
2π(n + 1)
Ã
sin
n+1
2
t
sin
1
2
t
!
2
≤ min
½
n + 1
2π
,
π
2(n + 1)t
2
¾
.
Indeed, K
n
(t) ≤ K
n
(0) =
n+1
2π
yields the first upper bound. And the inequality
|sint/2| ≥ (2/π)|t/2| = |t|/π on [−π, π] is enough to show that
1
2π(n + 1)
Ã
sin
n+1
2
t
sin
1
2
t
!
2
≤
1
2π(n + 1)
µ
1
|t|/π
¶
2
=
π
2(n + 1)t
2
.
The first bound is better for small |t|, and the second becomes an improvement at
the point δ = π/(n + 1).
14.7 Best Approximation by Trig Polynomials 497
This proof follows the proof of F
´
ejer’s Theorem using the additional informa-
tion contained in the Lipschitz condition to sharpen the error estimate. Looking
back at that proof, we obtain an estimate by splitting [−π, π] into two pieces. We
use the Lipschitz estimate |f(x + t) − f(x)| ≤ L|t|, and we take δ as found previ-
ously:
|σ
n
f(x) − f(x)| ≤
Z
π
−π
|f(x + t) − f (x)|K
n
(t) dt
≤
Z
δ
−δ
L|t|
n + 1
2π
dt +
Z
−δ
−π
+
Z
π
δ
L|t|
π
2(n + 1)t
2
dt
=
(n + 1)L
π
Z
π/n+1
0
t dt +
πL
(n + 1)
Z
π
π/n+1
t
−1
dt
=
(n + 1)L
π
π
2
2(n + 1)
2
+
πL
(n + 1)
log(n + 1)
=
Lπ
2(n + 1)
¡
1 + 2 log(n + 1)
¢
.
Finally, a little calculus shows that f (x) = (1 + 2logx)/x is decreasing for x >
√
e. So for n ≥ 2 we obtain
kσ
n
f − fk
∞
≤
Lπ
2n
(1 + 2 log n).
Now apply Theorem 14.7.2 to obtain
kf − S
n
fk
∞
≤ (3 + log n)
e
E
n
(f)
≤ (3 + log n) kf − σ
n
fk
∞
≤ (3 + log n)
Lπ
2n
(1 + 2 log n) ≤
Lπ
2n
4(1 + log n)
2
.
Now lim
n→∞
2πL(1 + logn)
2
n
= 0. Therefore, S
n
f converges uniformly to f. ¥
Exercises for Section 14.7
A. Show that if f is a Lipschitz function on [−π, π] with Lipschitz constant L, then the
Fourier coefficients satisfy |A
n
| ≤
2L
n
and |B
n
| ≤
2L
n
for n ≥ 1.
HINT: Split the integral into n pieces and replace each integral by
R
c
k
+π/n
c
k
−π/n
¡
f(x) − f(c
k
)
¢
sinnx dx. Then estimate each piece.
B. For a 2π-periodic continuous function f, define approximants P
2n
(f)(θ) =
A
0
+
n
X
k=1
A
k
coskθ+B
k
sinkθ+
n−1
X
k=1
(1−
k
n
)
¡
A
n+k
cos(n+k)θ+B
n+k
sin(n+k)θ
¢
.
(a) Show that P
2n
(f) = 2σ
2n−1
(f) − σ
n−1
(f).
(b) Hence deduce that kP
2n
(f)k
∞
≤ 3kfk
∞
.
(c) Show that if p ∈ TP
n
, then P
2n
(p) = p.

498 Fourier Series and Approximation
(d) Hence show that kf − P
2n
(f)k
∞
≤ 4
e
E
n
(f).
HINT: Follow the method of Theorem 14.7.2.
C. Use the previous exercise to obtain a lower bound
e
E
n
¡
|sinθ|
¢
> C/n.
HINT: See Exercise 13.6.B. Show:
¯
¯
P
2n
¡
|sinθ|
¢
(0)
¯
¯
≥
4
π
∞
P
k=n
1
4k
2
− 1
>
1
πn
.
D. Let 0 < α < 1. Recall that a 2π-periodic function f is of class Lipα if there is a
constant L so that |f(x) − f(y)| ≤ L|x − y|
α
for all −π ≤ y ≤ x ≤ π.
(a) If f ∈ Lipα, show that there is a constant C such that kf − σ
n
fk
∞
≤ Cn
−α
.
(b) Hence show that S
n
f converges uniformly to f.
HINT: Follow the proof of Theorem 14.7.3 using the new estimate.
E. Let f be a 2π-periodic function with Fourier coefficients A
n
and B
n
.
(a) Prove that (A
2
n
+ B
2
n
)
1/2
≤ ω(f;
π
n
).
HINT: Show that A
n
=
1
2π
Z
π
−π
¡
f(t) − f(t +
π
n
)
¢
cos(nt) dt.
(b) If f ∈ Lipα, prove that there is a constant C so that (A
2
n
+ B
2
n
)
1/2
≤ Cn
−α
.
(c) If f is C
p
and f
(p)
∈ Lipα, show that (A
2
n
+ B
2
n
)
1/2
≤ Cn
−p−α
.
F. Let f and g be 2π-periodic with Fourier series f ∼ A
0
+
P
n≥1
A
n
cosnθ + B
n
sinnθ
and g ∼ C
0
+
P
n≥1
C
n
cosnθ + D
n
sinnθ. Suppose that f is absolutely integrable and
g is Lipschitz. Prove that
1
2π
Z
π
−π
f(θ)g(θ) dθ = A
0
C
0
+
1
2
X
n≥1
A
n
C
n
+ B
n
D
n
.
HINT: Use Theorem14.7.3.
G. (a) Find the Fourier series of g(x) =
(
−x − π for −π ≤ x < 0
−x + π for 0 ≤ x ≤ π
(b) For n ≥ 1, define g
n
(x) = sin(2nx) S
n
g(x). Find the Fourier series for g
n
.
HINT: 2 sinA sinB = cos(A − B) − cos(A + B)
(c) Show that kg
n
k
∞
≤ π + 2. HINT: Use Exercise 14.6.E.
(d) Show that S
2n
g
n
(0) > logn.
HINT:
n
P
k=1
1
n
is an upper Riemann sum for
Z
n+1
1
1
x
dx.
(e) Hence prove that kg
n
− S
2n
g
n
k
∞
≥
logn
π + 2
e
E
2n
(g
n
). This shows that the logn
term is needed in Theorem 14.7.2.
(f) Show that h(x) =
∞
P
n=1
1
n
2
g
2·3
n
3
(x) is a continuous function such that S
3
n
3
h(0)
diverges. NOTE: This is difficult.
14.8. Connections with Polynomial Approximation
We will now connect trigonometric polynomial approximation with polyno-
mial approximation on an interval by exploiting an important connection between
trig polynomials and the Chebychev polynomials of Section 10.7.

14.8 Connections with Polynomial Approximation 499
The idea is to relate each function f in C[−1, 1] to an even function Φf in
C[−π, π] in such a way that the set P
n
of polynomials of degree n is carried into
TP
n
. This map is defined by
Φf(θ) = f(cos θ) for − π ≤ θ ≤ π.
Notice immediately that since cosθ takes values in [−1, 1], the right-hand side is
always defined. Also,
Φf(−θ) = f(cos(−θ)) = f(cosθ) = Φf(θ).
Thus Φf is even.
A crucial property of the map Φ is that it is linear. Observe that for f, g in
C[−1, 1] and α, β in R,
Φ(αf + βg)(θ) = (αf + βg)(cosθ) = αf(cosθ) + βg(cosθ)
= αΦf(θ) + βΦg(θ) = (αΦf + βΦg)(θ).
So Φ(αf + βg) = αΦf + βΦg, which is linearity.
Recall from Definition 10.7.1 that the Chebychev polynomials are defined on
the interval [−1, 1] by T
n
(x) = cos(n cos
−1
x). Since T
n
is a polynomial of degree
n, every polynomial can be expressed as a linear combination of the T
n
s, and, in
particular, P
n
is spanned by {T
0
, . . . , T
n
}. Also recall that there is an inner product
on C[−1, 1] given by
hf, gi
T
=
1
π
Z
1
−1
f(x)g(x)
dx
√
1 − x
2
for f, g ∈ C[−1, 1].
The Chebychev polynomials form an orthonormal set by Lemma 10.7.5.
Notice that
ΦT
n
(θ) = cos(n cos
−1
(cosθ)) = cos(nθ).
It follows that Φ maps P
n
onto the span of {1, cosθ, . . . , cosnθ}, which consists
of the even trig polynomials in TP
n
.
This establishes the first parts of the following theorem. Let E[−π, π] denote
the closed subspace of C[−π, π] consisting of all even continuous functions on
[−π, π].
14.8.1. THEOREM. The map Φ of C[−1, 1] into E[−π, π] satisfies the follow-
ing:
(1) Φ is linear, one-to-one, and onto.
(2) ΦT
n
(θ) = cos(nθ) for all n ≥ 0.
(3) Φ(P
n
) = E[−π, π] ∩ TP
n
.
(4) kΦf − Φgk
∞
= kf − gk
∞
for all f, g ∈ C[−1, 1].
(5) E
n
(f) =
e
E
n
(Φf) for all f ∈ C[−1, 1].
(6) hf, gi
T
= hΦf, Φgi for all f, g ∈ C[−1, 1].
500 Fourier Series and Approximation
PROOF. For (1), linearity has already been established. To see that Φ is one-to-one,
suppose that Φf = Φg for functions f, g in C[−1, 1]. Then f(cosθ) = g(cosθ) for
all θ in [−π, π]. Since cos maps [−π, π] onto [−1, 1], it follows that f (x) = g(x)
for all x in [−1, 1]. Thus f = g as required.
To show that Φ is surjective, we construct the inverse map from E[−π, π] to
C[−π, π]. For each even function g in E[−π, π], define a function Ψg in C[−1, 1]
by
Ψg(x) = g(cos
−1
x).
(Notice that cos
−1
takes all values in [0, π]. So Ψg depends only on g(θ) for θ in
[0, π]. This is fine because g is even.) Compute
ΦΨg(θ) = Ψg(cosθ) = g(cos
−1
(cosθ)) = g(|θ|) = g(θ).
So Φ maps Ψg back onto g, showing that Φ maps onto E[−π, π].
We proved (2) and (3) in the discussion before the theorem. Now consider (4).
Note that
kΦfk
∞
= sup
θ∈[−π,π]
|f(cosθ)| = sup
x∈[−1,1]
|f(x)| = kfk
∞
.
Hence by linearity,
kΦf − Φgk
∞
= kΦ(f − g)k
∞
= kf − gk
∞
.
Applying this, we obtain
E
n
(f) = inf{kf − pk
∞
: p ∈ P
n
}
= inf{kΦf − Φpk
∞
: p ∈ P
n
}
= inf{kΦf − qk
∞
: q ∈ TP
n
∩ E[−π, π]}.
However, since Φf is even, the trig polynomial in TP
n
closest to Φf is also even.
To see this, suppose that r ∈ TP
n
satisfies kΦf − rk =
e
E
n
(Φf), and let
q(θ) =
r(θ) + r(−θ)
2
.
You should verify that if r(θ) = a
0
+
P
n
k=1
a
n
coskθ + b
n
sinθ, then q(θ) =
a
0
+
P
n
k=1
a
n
coskθ. Then q belongs to TP
n
∩ E[−π, π] and
|Φf(θ) − q(θ)| =
¯
¯
¯
¯
Φf(θ) + Φf(−θ)
2
−
r(θ) + r(−θ)
2
¯
¯
¯
¯
≤
1
2
¯
¯
Φf(θ) − r(θ)
¯
¯
+
1
2
¯
¯
Φf(−θ) − r(−θ)
¯
¯
≤
1
2
e
E
n
(Φf) +
1
2
e
E
n
(Φf) =
e
E
n
(Φf).
Hence kΦf −qk
∞
=
e
E
n
(Φf). Putting this information into the preceding inequal-
ity, we obtain E
n
(f) =
e
E
n
(Φf).
14.8 Connections with Polynomial Approximation 501
Finally, to prove (6), we make the substitution x = cosθ in the integral.
hf, gi
T
=
1
π
Z
1
−1
f(x)g(x)
dx
√
1 − x
2
=
1
π
Z
0
π
f(cosθ)g(cos θ)
−sinθ dθ
sinθ
=
1
2π
Z
π
−π
f(cosθ)g(cos θ) dθ = hΦf, Φgi
¥
In summary, this theorem shows that C[−1, 1] with the inner product h·, ·i
T
and E[−π, π] with the inner product h·, ·i are, as inner product spaces, the same.
Approximation questions for Fourier series are well studied, and this allows a
transference to polynomial approximation. The reason we obtain estimates more
readily in the Fourier series case is that the periodicity allows us to obtain nice
integral formulas for our approximations.
Part (6) of this theorem shows that the Chebychev series for f ∈ C[−1, 1]
correspond to the Fourier series of Φf as f ∼
∞
P
k=0
a
k
T
k
, where
a
0
= hf, 1i
T
and a
n
= 2hf, T
n
i
T
for n ≥ 1.
Then define two series corresponding to the Dirichlet and Ces
`
aro series.
C
n
f =
n
X
k=0
a
k
T
k
and Σ
n
f =
n
X
k=0
¡
1 −
k
n + 1
¢
a
k
T
k
Now it is just a matter of reinterpreting the Fourier series results for polynomials
using Theorem 14.8.1.
14.8.2. THEOREM. Let f be a continuous function on [−1, 1] with Chebychev
series
P
∞
k=0
a
k
T
k
. Then (Σ
n
f)
∞
n=1
converges uniformly to f on [−1, 1]. If f is
Lipschitz, then (C
n
f)
∞
n=1
also converges uniformly to f. In any event,
kf − C
n
fk
∞
≤ (3 + log n)E
n
(f).
PROOF. The map Φ converts the problem of approximating f by polynomials of
degree n to the problem of approximating Φf by trig polynomials of degree n.
Property (6) of Theorem 14.8.1 shows that ΦC
n
f = S
n
Φf and ΦΣ
n
f = σ
n
Φf.
So the fact that Σ
n
f converge uniformly to f on [−1, 1] is a restatement of F
´
ejer’s
Theorem (Theorem 14.6.4).
If f has a Lipschitz constant L, then
|Φf(α) − Φf(β)| = |f(cosα) − f(cos β)|
≤ L|cosα − cos β| ≤ L|α − β|.
The last step follows from the Mean Value Theorem since the derivative of cosθ is
sinθ, which is bounded by 1. Thus Φf is Lipschitz with the same constant. (Warn-
ing: This step is not reversible.) By Theorem 14.7.3, the sequence S
n
Φf converges
uniformly to Φf, whence C
n
f converges uniformly to f by Theorem 14.8.1(4).
502 Fourier Series and Approximation
Theorem 14.7.2 and Theorem 14.8.1(4) provide the estimate
kf − C
n
fk
∞
= kΦf − S
n
fk
∞
≤ (3 + log n)
e
E
n
(Φf) = (3 + logn)E
n
(f).
¥
14.8.3. EXAMPLE. Let us try to approximate f(x) = |x| on [−1, 1]. We con-
vert this to the function
g(θ) = Φf(θ) = |cosθ| for − π ≤ θ ≤ π.
This is an even function and thus has a cosine series. Also, g(π − θ) = g(θ). The
functions cos2nθ have this symmetry, but
cos
¡
(2n + 1)(π − θ)
¢
= −cos(2n + 1)θ.
So A
2n+1
= 0 for n ≥ 0. Compute
A
0
=
1
2π
Z
π
−π
|cosθ|dθ =
2
π
and for n ≥ 1,
A
2n
=
1
π
Z
π
−π
|cosθ|cos2nθ dθ
=
4
π
Z
π/2
0
cosθ cos2nθ dθ
=
2
π
Z
π/2
0
cos(2n − 1)θ + cos(2n + 1)θ dθ
=
2
π
sin(2n − 1)θ
2n − 1
+
2
π
sin(2n + 1)θ
2n + 1
¯
¯
¯
¯
π/2
0
=
2
π
µ
(−1)
n−1
2n − 1
+
(−1)
n
2n + 1
¶
=
(−1)
n−1
4
π(4n
2
− 1)
.
These coefficients are absolutely summable since they behave like the series
1/n
2
. Thus S
n
g converges uniformly to g by the Weierstrass M-test (see Exer-
cise 13.4.D). Hence by Theorem 14.8.1, the sequence of polynomials
C
2n
f(x) =
2
π
−
4
π
n
X
k=1
(−1)
k
4k
2
− 1
T
2k
(x)
converges to |x| uniformly on [−1, 1].
