Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

14.3 The Riemann–Lebesgue Lemma 473

Let us compute the Fourier coefﬁcients of f. Since f is odd, we need only

compute the sine terms. We integrate by parts three times.

−π

(θ

− π

θ) sinnθ dθ

− π

−cosnθ

−π

3θ

− π

nπ

cosnθ dθ

= 0 +

3θ

− π

sinnθ

−π

−

−π

6θ

sinnθ dθ

= 0 +

6θ

cosnθ

−π

−

−π

cosnθ dθ

6π

(−1)

−

−6π

(−1)

− 0

(−1)

In particular, we see that these coefﬁcients satisfy

∞

n=1

(−1)

= 12

∞

n=1

< ∞.

Therefore, by the Weierstrass M-test, this series converges uniformly to a continu-

ous function. By Corollary 13.6.3, this series must converge to f uniformly on the

whole circle. Therefore,

− π

θ =

∞

n=1

(−1)

sinnθ

for all θ ∈ [−π, π].

For example, plug in θ = π/2. Note that sin(2k + 1)π/2 = (−1)

and

sin(2k)π/2 = 0. So

− π

∞

k=0

(−1)

2k+1

(2k + 1)

(−1)

Solving, we ﬁnd that

∞

k=0

(−1)

(2k + 1)

Now consider the derivative f

(θ) = 3θ

− π

. The Fourier series may be

differentiated term by term. We may apply Exercise 13.4.E since

∞

n=1

n|B

| =

∞

n=1

< ∞

474 Fourier Series and Approximation

to obtain another uniformly convergent series

3θ

− π

∞

n=1

(−1)

cosnθ for − π ≤ θ ≤ π.

Let us substitute θ =

here as well. Here cos

(2k+1)π

= 0 and cos

2kπ

= (−1)

−

∞

k=1

(−1)

= −3

∞

k=1

(−1)

k−1

Therefore,

∞

k=1

(−1)

k−1

∞

k=1

− 2

∞

k=1

(2k)

∞

k=1

So we again obtain Euler’s sum

∞

k=1

Now we have to work harder to enlarge the class of functions. An important

step in establishing convergence is the apparently modest goal of showing that at

least the Fourier coefﬁcients converge to 0. This is clearly a necessary condition for

any kind of convergence. This was by no means clear in the 1850s when Riemann

did his fundamental work. In fact, he introduced the modern notion of integral,

which we studied in Chapter 6, in order to address the question of convergence of

Fourier series.

14.3.3. THE RIEMANN–LEBESGUE LEMMA.

If f is piecewise continuous on [a, b] and τ ∈ R, then

lim

n→∞

f(x) sin(nx + τ) dx = 0.

PROOF. The assumption that f is piecewise continuous is much stronger than is

really necessary. The result is true for all absolutely integrable functions. However,

the proof is more difﬁcult.

We may assume that b − a ≤ π. For otherwise, we just chop the interval

[a, b] into pieces of length at most π and prove the lemma on each piece separately.

Translation by a multiple of π does not affect anything except possibly the sign of

the integral. So we may assume that [a, b] is contained in [−π, π]. Now extend the

deﬁnition of f to all of [−π, π] by setting f(x) = 0 outside of [a, b]. This is still

piecewise continuous, and the integrals are unchanged.

14.3 The Riemann–Lebesgue Lemma 475

We use the fact established in the last section that

∞

n=1

+ B

= kf k

< ∞.

Since the terms of a convergent series must tend to 0, we have

lim

n→∞

+ B

= 0.

So we compute

−π

f(x) sin(nx + τ) dx

−π

f(x) cosnx sinτ + sinnx cosτ dx

sinτ + B

cosτ

≤

+ B

The last estimate (which is included only for elegance) used the Cauchy–Schwarz

inequality. This establishes the desired limit. ¥

14.3.4. COROLLARY. If f is a piecewise continuous 2π-periodic function with

Fourier series

f ∼ A

∞

n=1

cosnθ + B

sinnθ,

then lim

n→∞

= lim

n→∞

= 0.

PROOF. Take the deﬁnitions of A

and B

and apply the Riemann–Lebesgue

Lemma for the interval [−π, π] and displacements τ = π/2 and τ = 0, respec-

tively. ¥

Exercises for Section 14.3

A. (a) Let 0 < a ≤ π. Compute the Fourier series for f(θ) = max{a − |θ|, 0}.

(b) Show that this series converges uniformly to f . Evaluate f(0) in two ways.

n≥1

cosna

B. (a) Find the Fourier series for f(θ) =

(

sinθ if 0 ≤ θ ≤ π

0 if − π ≤ θ ≤ 0

(b) Evaluate

n≥1

(−1)

− 1

C. Let f(x) = sin

for 0 < |x| ≤ π and f(0) = 0. This is not piecewise continuous.

Show that f is the limit of a sequence of continuous functions in the L

norm. Hence

show that the Fourier coefﬁcients of f tend to 0.

D. Suppose that f is an absolutely integrable function for which there is a sequence of

continuous functions g

so that lim

n→∞

kf − g

= 0. Prove the Riemann–Lebesgue

Lemma for f.

476 Fourier Series and Approximation

E. Let f be a monotone function on [−π, π]. Prove that the Fourier coefﬁcients satisfy

max{|A

|, |B

|} ≤

nπ

, where M = |f(π) − f(−π)|.

HINT: Express B

as the sum of integrals over intervals on which sinnθ has constant

sign, and combine into a single integral.

F. Consider the DE y

+ 4y = g, where g is an odd C

function with Fourier series

n≥1

sinnx.

(a) If B

= 0, ﬁnd the Fourier series of the solution.

(b) Verify that this series and its second derivative converge uniformly and thus provide

a solution.

x cos2x is the solution for g(x) = sin2x.

G. Let g be an odd function such that g(θ) ≥ 0 on [0, π].

(a) Show by induction that |sinnθ| < n sinθ on (0, π).

(b) Prove that the Fourier coefﬁcients satisfy |B

| < nB

general.

H. (a) Show that for any a < b and any real values of α

, n ≥ 1,

liminf

n→∞

|cos(nx + α

)|dx ≥

b − a

HINT: |cos(nx + α

)| ≥ cos

(nx + α

). Express this square in terms of cos 2nx

and sin2nx.

(b) Show that if r

are positive numbers such that

∞

n=1

|cos(nx + α

)| ≤ C for all

a ≤ x ≤ b, then

∞

n=1

< ∞.

I. Prove the Riemann–Lebesgue Lemma for absolutely integrable functions.

HINT: approximate the function by a step function in the L

norm.

14.4. Pointwise Convergence of Fourier Series

In order to establish a more delicate convergence theorem, a better method is

needed for computing the partial sums of the Fourier series. It turns out that there is

an integral formula using the Dirichlet kernel, which we deﬁne in a moment. This

new kernel is not nearly as nicely behaved as the Poisson kernel. Nevertheless,

it provides a better method for achieving good estimates than crudely estimating

individual terms.

14.4.1. DEFINITION. The sequence of functions D

given by

(t) =











2n + 1

2π

if t = 2πm, m ∈ Z

sin(n +

2π sint/2

if t 6= 2πm,

14.4 Pointwise Convergence of Fourier Series 477

for n = 1, 2, . . . is called the Dirichlet kernel.

To see that D

is continuous at zero, compute

lim

t→0

(t) = lim

t→0

sin(n +

2π sint/2

n +

2π/2

2n + 1

2π

The following theorem connects D

to Fourier series.

14.4.2. THEOREM. Let f be a piecewise continuous and 2π-periodic function.

Then

f(x) =

−π

f(x + t)D

(t) dt.

PROOF. If we substitute the formulae for A

and B

into the deﬁnition of S

then we obtain

f(x) = A

k=1

coskx + B

sinkx

2π

−π

f(t) dt +

k=1

−π

f(t) coskt dt coskx+

k=1

−π

f(t) sinkt dt sinkx

2π

−π

f(t)

1 + 2

k=1

coskt coskx + sinkt sinkx

2π

−π

f(t)

1 + 2

k=1

cosk(t − x)

using the identity cos(A − B) = cosA cosB + sinA sin B. Then, substituting

u = t − x and using the 2π-periodicity of f, we have

−π

f(x + u)

2π

k=1

cosku

du.

So to complete the proof, it is enough to prove the trig identity

2π

1 + 2

k=1

cosku

sin(n +

2π sin(u/2)

= D

(u).

This identity may be computed by using complex exponentials as we did in

Lemma 13.10.4. Here we give a strictly real variable argument using the trig iden-

tity 2 sin A cos B = sin(A + B) − sin(A − B). We set up a telescoping sum, as

478 Fourier Series and Approximation

follows:

sin

1 + 2

k=1

cosku

= sin

k=1

2sin

cosku

= sin

k=1

sin(k +

)u − sin(k −

= sin(n +

= 2π sin

sin(n +

2π sinu/2

provided u 6= 0. If u = 0, then we have

2π

1 + 2

k=1

cos0

2n + 1

2π

= D

(0),

and so the trig identity holds for all u. ¥

We collect here various properties of the functions D

that we will need later.

What makes the Dirichlet kernel signiﬁcantly inferior to the Poisson kernel is that

the Dirichlet kernel is not positive. Indeed, the following properties (2) and (3)

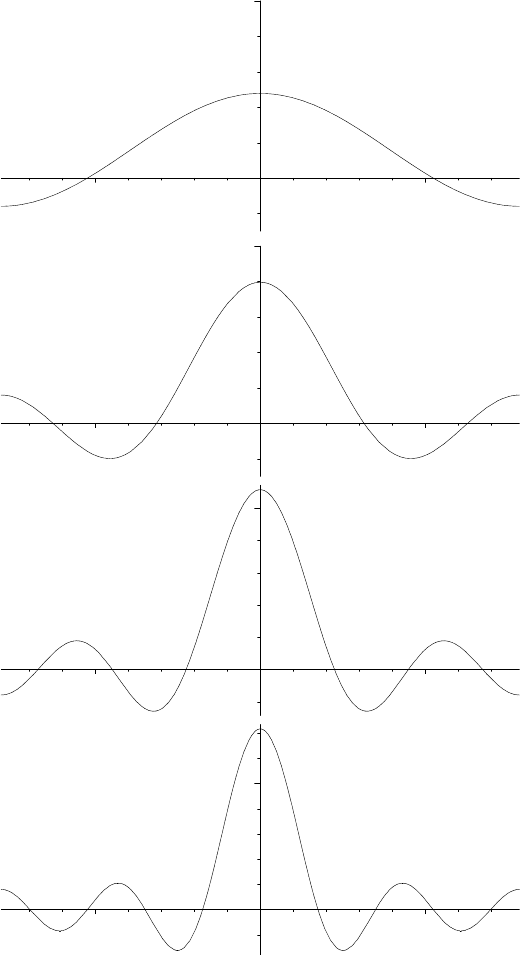
together show that signiﬁcant cancellation must occur in (2). Compare Figure 14.2

with Figure 13.2.

14.4.3. PROPERTIES OF THE DIRICHLET KERNEL.

The Dirichlet kernel D

satisﬁes the following properties:

(1) For each n, D

is a continuous, 2π-periodic, even function.

(2)

−π

(t) dt = 1.

(3) For each n, .28 + .4logn ≤

−π

| ≤ 2 + log n

PROOF. By periodicity, it sufﬁces to show D

is continuous at 0. Continuity at

0 follows from the limit computed just after the deﬁnition. The identity D

(t) =

2π

1 + 2

k=1

coskt

shows that D

is even and 2π-periodic.

If f(θ) = 1 for all θ, then the Fourier series of f is just f ∼ 1. Therefore,

f = 1 for all n ≥ 1. Using the integral formula of Theorem 14.4.2, we have

1 =

−π

(t) dt,

which proves (2).

14.4 Pointwise Convergence of Fourier Series 479

–2 2

FIGURE 14.2. The graphs of D

, D

, and D

480 Fourier Series and Approximation

The reader can check that

−π

(t)|dt =

−π

|1 + 2 cos t|

2π

dt < 1.5. To

provide the upper bound on

| for n ≥ 2, we ﬁrst observe that

−π

(t)|dt = 2

(t)|dt =

1/n

2|D

(t)|dt +

1/n

sin(n +

π sint/2

dt.

The ﬁrst integral is estimated for n ≥ 2 as

1/n

2|D

(t)|dt =

1/n

1 + 2

k=1

coskt

≤

(1 + 2n) ≤

2.5

< 0.8.

For the second integral, we use the inequalities π sin(t/2) ≥ t for t ≥ 0 and

|sin(n +

)t| ≤ 1 to obtain

1/n

sin(n + 1/2)t

π sint/2

dt ≤

1/n

dt = log π − log

< 1.2 + log n.

Combining these two integrals, we have

−π

(t)|dt ≤ 2 + logn.

For the lower bound, ﬁrst note that

(k+1)π/(2n+1)

kπ/(2n+1)

|sin(n + 1/2)t|dt =

π/(2n+1)

sin(n + 1/2)t dt

2n + 1

π/2

sint dt =

2n + 1

Now use the fact that sint ≤ t for t ≥ 0 to obtain

−π

(t)|dt = 2

sin(n + 1/2)t

2π sint/2

dt ≥ 2

sin(n +

πt

= 2

k=0

(k+1)π/(2n+1)

kπ/(2n+1)

|sin(n + 1/2)t|

πt

≥ 2

k=0

2n + 1

(k + 1)π

(k+1)π/(2n+1)

kπ/(2n+1)

|sin(n + 1/2)t|dt

≥ 2

k=0

2n + 1

(k + 1)π

2n + 1

k=0

k + 1

14.4 Pointwise Convergence of Fourier Series 481

The integral test shows that

k=0

(k + 1)

−1

≥ log(2n + 2), so

−π

(t)|dt ≥

(log2 + log(n + 1))

> .28 + .4 log n.

This integral formula will now be used to establish convergence for reasonably

nice functions. The argument has some similarity to the Poisson Theorem, but

property (3) of the previous proposition forces us to be somewhat circumspect. At

a certain point, we will need to combine a Lipschitz condition with the Riemann–

Lebesgue Lemma to obtain the desired estimate.

14.4.4. DEFINITION. A function f is piecewise Lipschitz if f is piecewise

continuous, and there is a constant L so that f is has Lipschitz constant at most L

on each interval of continuity.

A function f is piecewise C

on [a, b] if f is differentiable except at ﬁnitely

many points, and f

is piecewise continuous.

For example, the Heaviside function H from Example 5.2.2 is piecewise C

Another example is f(x) = x −bxc, where bxc indicates the largest integer n ≤ x.

The cubic function f in Example 14.3.2 is piecewise C

and f

is piecewise C

Being piecewise C

implies piecewise Lipschitz with constant L = kf

∞

. In-

deed, observe that f

is bounded on each (closed) interval on which it is continuous

because of the Extreme Value Theorem (Theorem 5.4.4); and hence it is bounded

on [−π, π]. On any interval of continuity for f

, the Mean Value Theorem shows

that

|f(x) − f(y)| ≤ kf

∞

|x − y|.

These estimates can then be spliced together when the function is continuous on an

interval even if the derivative is not continuous.

For an example of a Lipschitz function that is not C

, consider f (x) = x

sin

for x 6= 0 and f (0) = 0. The derivative is deﬁned everywhere:

(x) =

(

2x sin

− cos

for x 6= 0

0 for x = 0.

This is bounded by 3 on all of R, so the Mean Value Theorem argument is valid.

However, f

has a nasty discontinuity at the origin. So f

is not piecewise continu-

ous.

Dirichlet proved a crucial special case of this result in 1829. In his treatise, he

introduced the notion of a function which is in use today. Prior to that period, a

function was typically assumed to be given by a single analytic formula.

482 Fourier Series and Approximation

14.4.5. THE DIRICHLET–JORDAN THEOREM.

Suppose that a function f on R is 2π-periodic and piecewise Lipschitz. If f is

continuous at θ, then

lim

n→∞

f(θ) = f(θ).

If f has a jump discontinuity at θ, then

lim

n→∞

f(θ) =

f(θ

) + f(θ

−

)

PROOF. By Theorem 14.4.3 (2),

f(θ

) = f (θ

)

−π

(t) dt = 2

f(θ

(t) dt

and a similar equality holds for f(θ

−

). Using Theorem 14.4.2,

f(θ) =

−π

f(θ − t)D

(t) dt

f(θ + t) + f (θ − t)

(t) dt.

Using this formula for S

f(θ) with the previous two equalities gives

f(θ) −

f(θ

) + f(θ

−

)

f(θ + t) + f (θ − t)

(t) dt −

f(θ

) + f(θ

−

)

(t) dt

f(θ + t) − f (θ

)

(t) dt +

f(θ − t) − f (θ

−

)

(t) dt.

We now consider these two integrals separately. First we prove that

lim

n→∞

f(θ + t) − f (θ

)

(t) dt = 0.

An entirely similar argument will show the second integral also goes to zero as n

goes to inﬁnity. Combining these two results proves the theorem.

Let L be the Lipschitz constant for f, and let ε > 0 be given. Choose a positive

δ < ε/L that is so small that f is continuous on [θ, θ + δ]. Hence

|f(θ + t) − f (θ

)| < Lt for all θ + t ∈ [θ, θ + δ].

Since |sin(t/2)| ≥ |t|/π for all t in [−π, π], it follows that

(t)| =

sin(n +

2π sint/2

≤

2|t|

− π ≤ t ≤ π.

Therefore,

f(θ + t) − f (θ

)

(t) dt

≤

dt ≤

Lδ