Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

13.7 The Maximum Principle 443

is a trigonometric polynomial such that

kf − t

∞

≤ kf − f

∞

+ kf

− t

∞

≤

∞

k=K+1

coskθ + B

sinkθ

≤

∞

k=N +1

4Mr

Therefore, (t

)

∞

n=1

converges uniformly to f . ¥

Exercises for Section 13.6

A. (a) Compute the Fourier series of f(θ) = θ

for −π ≤ θ ≤ π.

(b) Hence evaluate

n≥1

(−1)

B. (a) Compute the Fourier series of the function f(θ) = |sinθ|.

(b) Hence evaluate

n≥1

(−1)

− 1

C. Suppose that Q(r, θ) is any function on D satisfying properties (1), (3), and (5) of

Proposition 13.5.2. If f is a continuous function on the unit circle, deﬁne v(r, θ) =

−π

f(θ − t)Q(r, t) dt. Prove that f

(θ) = v(r, θ) converges to f uniformly on

[−π, π].

D. Use rectangular coordinates for the disk D = {(x, y) : x

+ y

< 1}, and deﬁne a

function u(x, y) = tan

−1

1 + x

(a) Show that ∆u = u

+ u

= 0.

(b) Show that u is continuous on D except at (−1, 0).

f(θ) := lim

r→1

−

u(r cosθ, r sin θ).

(d) Find the Fourier series for f, and hence ﬁnd an expression for u in polar coordi-

nates.

13.7. The Maximum Principle

The remaining point to be dealt with in the heat problem is the question of

uniqueness of solutions. Physically, it is intuitively clear that a ﬁxed temperature

distribution on the boundary circle will result in a uniquely determined distribution

over the whole disk. We will show this to be the case by establishing a maximal

principle showing that a harmonic function must take its maximum value on the

boundary circle.

444 Fourier Series and Physics

13.7.1. MAXIMUM PRINCIPLE.

Suppose that u is continuous on the closed disk D and ∆u = 0 on the open disk D.

Then

max

(r,θ)∈D

u(r, θ) = max

−π≤θ≤π

u(1, θ).

PROOF. First suppose that v(r, θ) satisﬁes ∆v ≥ ε > 0. If v attained its maximum

at an interior point (r

, θ

), then the ﬁrst-order partial derivatives are zero,

, θ

) = 0 = v

, θ

and the second-order derivatives are negative,

, θ

) ≤ 0 and v

θθ

, θ

) ≤ 0.

Therefore,

ε ≤ ∆v(r

, θ

) = v

, θ

) +

, θ

) +

θθ

, θ

) ≤ 0.

This contradiction shows that v attains its maximum only on the boundary.

Now consider u. Let v

(r, θ) = u(r, θ) +

. A simple computation shows

that

∆v

= ∆u +

∆r

)

θθ

> 0.

So v

attains it maximum only on the boundary circle. Since v

converges uni-

formly to u, we obtain

max

(r,θ)∈

u(r, θ) = lim

n→∞

max

(r,θ)∈D

(r, θ)

= lim

n→∞

max

−π≤θ≤π

(1, θ) = max

−π≤θ≤π

u(1, θ).

13.7.2. COROLLARY. Suppose that u is continuous on the closed disk

D and

∆u = 0 on the open disk D and u(1, θ) = 0 for −π ≤ θ ≤ π. Then u = 0.

PROOF. By the Maximum Principle, u(r, θ) ≤ 0 on D. However, −u is also

a continuous harmonic function, and thus the Maximum Principle implies that

u(r, θ) ≥ 0 on D. Hence u = 0. ¥

All the ingredients are now in place for a complete solution to the heat problem

on the disk.

13.7.3. THEOREM. Let f(θ) be a continuous 2π-periodic function. There ex-

ists a unique solution to the steady-state heat problem

∆u = 0 u(1, θ) = f(θ)

given by the Poisson integral of f.

13.7 The Maximum Principle 445

PROOF. By Corollary 13.6.2, the Poisson integral of f provides a solution u(r, θ)

to the heat problem. It remains to discuss uniqueness. Suppose that v(r, θ) is

another solution. Then consider w(r, θ) = u(r, θ) − v(r, θ). It follows that

∆w = ∆u − ∆v = 0 and w(1, θ) = u(1, θ) − v(1, θ) = 0.

Thus by Corollary 13.7.2, w = 0 and so v = u is a only solution. ¥

Exercises for Section 13.7

A. Suppose that u(x, y) is a solution of the heat problem on the disk D written in rectan-

gular coordinates for convenience. Let D

, y

) be a small disk contained inside D.

Establish the mean value property:

u(x

, y

) =

2π

u(x

+ R cosθ, y

+ R sinθ) dθ.

HINT: The restriction of u to

, y

) is the solution to the heat problem on this

disk. Use the Poisson formula for the value at the centre of the disk.

B. (a) Suppose that u(x, y) is a continuous function on D that satisﬁes the mean value

property of the previous exercise. Prove that u attains its maximum on the bound-

ary.

(b) Moreover, prove that if u attains its maximum value at a single interior point, then

it must be constant.

C. Prove that a continuous function on D that satisﬁes the mean value property is har-

monic.

HINT: Fix a point (x

, y

) in D and let D

, y

) be a small disk contained inside D.

Let v(x, y) be the solution of the steady-state heat problem on D

, y

) that agrees

with u on the boundary circle. Showthat u = v, and hence deduce that ∆u(x

, y

) = 0.

D. Let u(x, y) be a positive harmonic function on an open subset Ω of the plane. Suppose

that D

, y

) is contained in Ω. Prove that

R − r

R + r

u(x

, y

) ≤ u(x

+ r cos θ, y

+ r sin θ) ≤

R + r

R − r

u(x

, y

) for 0 ≤ r < R.

HINT: Compare Exercise 13.5.D.

E. Let Ω be a bounded open subset of the plane with smooth boundary Γ. A function v

on Ω is harmonic if ∆v = 0 on Ω.

(a) Show that if in addition v is continuous on

Ω, then it must attain its maximum value

on Γ.

(b) Hence show that if f is a continuous function on Γ, there is at most one continuous

function on Ω that is harmonic on Ω and with boundary values equal to f.

F. Let u(r, θ) =

r(1 − r

) sinθ

(1 − 2r cos θ + r

)

on D.

(a) Prove that u is harmonic on D.

(b) Show that lim

r→1

−

u(r, θ) = 0 for all values of θ.

(d) Is u bounded?

446 Fourier Series and Physics

13.8. The Vibrating String (Formal Solution)

The mathematics of a vibrating string was one of the ﬁrst problems studied

using Fourier series. It arose in a discussion on the oscillations of a violin string by

d’Alembert in 1747, twenty-two years before Fourier was born.

Most readers will be familiar with swinging a skipping rope. The simplest

mode is a single lobe oscillating between the two ﬁxed ends. However, it is possible

to set up a wave with two lobes or even three. These vibrations with more lobes are

called harmonics. They exist in the vibration of any stringed instrument and tend

to be characteristic of the instrument, giving it a distinctive sound. For example,

violins have signiﬁcant order ﬁve harmonics.

Our problem is to describe the motion of a vibrating string. We imagine a

uniform string stretched between two ﬁxed endpoints under tension. We further

assume that the oscillations are small compared with the length of the string. This

is a reasonable assumption for a stiff string like one found on a violin or piano.

This leads to the simplifying assumption that each point on the string moves only

in a vertical direction. We ignore all forces other than the effect of string tension,

such as the weight of the string and air resistance.

Orient the string along the x-axis of the plane, and choose units so that the

endpoints are (0, 0) and (π, 0). The vertical displacement of the string will be

given by a function y(x, t), the function giving the horizontal position at the point

x ∈ [0, π] at the time t. For convenience, we assume that time begins at time t = 0.

Let τ denote the tension force, and let ρ be the density of the string.

Fix x and t and consider the forces acting on the string segment between the

nearby points A = (x, y) =

x, y(x, t)

and B = (x + ∆x, y + ∆y), where

y + ∆y = y(x + ∆x, t). The tension τ on the string results in forces acting on both

ends of the segment in the direction of the tangent, as shown in Figure 13.3.

x + ∆x

FIGURE 13.3. Forces acting on a segment of the string.

The force at A is

−τ

∂y

∂x

(x, t)

1 +

∂y

∂x

(x, t)

≈

− τ, −τ

∂y

∂x

(x, t)

The approximation is reasonable since y and

∂y

∂x

are assumed to be small relative to

1. Likewise, the tensile force at B is approximately

τ, τ

∂y

∂x

(x + ∆x, t)

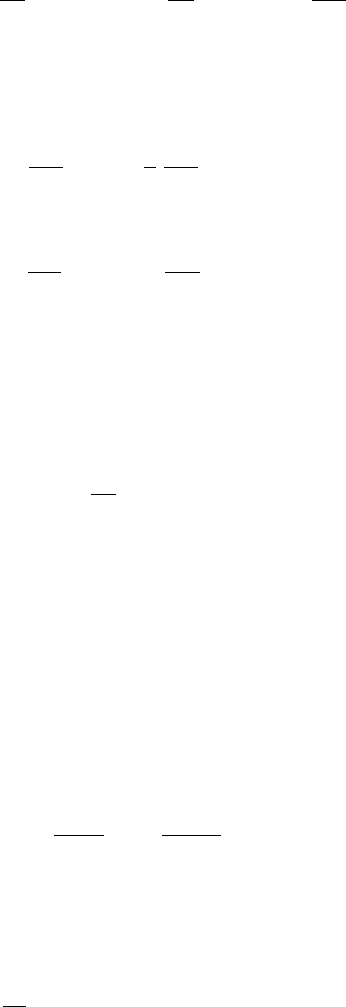
13.8 The Vibrating String (Formal Solution) 447

The horizontal forces cancel, while the combined vertical force is

∆V (x, t) = τ

∂y

∂x

(x + ∆x, t) − τ

∂y

∂x

(x, t) ≈ τ ∆x

∂

∂x

(x, t).

By Newton’s law, we have F = ma, where we have a segment of mass ρ∆x and

acceleration equal to the second derivative of y(x, t) with respect to t. Substitute

this in, divide by ρ∆x, and take the limit as ∆x tends to 0 to obtain the linear partial

differential equation

∂

∂t

(x, t) =

∂

∂x

(x, t).

Set ω

= τ /ρ. This is known as the one-dimensional wave equation:

(13.8.1)

∂

∂t

(x, t) = ω

∂

∂x

(x, t).

Since the endpoints are ﬁxed, there are boundary conditions

(13.8.2) y(0, t) = y(π, t) = 0 for all t ≥ 0.

Finally, there are initial conditions: Imagine the string is initially stretched to some

(continuous) shape f(x) and moving with initial velocity g(x). This gives the

conditions

(13.8.3) y(x, 0) = f (x),

∂y

∂t

(x, 0) = g(x) for all x ∈ [0, π].

These boundary conditions, together with the wave equation governing subsequent

motion of the string, determine a unique solution. We shall see that it can be solved

in a manner similar to our analysis of the steady-state heat problem.

As before, we begin by using separation of variables to look for solutions of the

special form y(x, t) = X(x)T (t). There is no way to know in advance that there

are solutions of this type, but in fact there are many such solutions that can be then

be combined to exhaust all possibilities. Substituting y(x, t) = X(x)T (t) into the

wave equation gives

X(x)T

(t) = ω

(x)T (t).

Isolating the variables x and t, we obtain

(t)

T (t)

= ω

(x)

X(x)

The left-hand side of this equation is independent of x and the right-hand is be

independent of t. Thus both sides are independent of both variables and therefore

are equal to some constant c.

This results in two ordinary differential equations:

(x) −

X(x) = 0 and T

(t) − cT (t) = 0.

The boundary condition (13.8.2) simpliﬁes to yield X(0) = X(π) = 0. At this

stage, we must ignore the initial shape conditions (13.8.3).

448 Fourier Series and Physics

The equation for X is essentially the same as the equation for Θ in Section 13.2.

Depending on the sign of c, the solutions are sinusoidal, linear, or exponential:

X(x) = A cos

√

|c|

+ B sin

√

|c|

for c < 0

X(x) = A + Bx for c = 0

X(x) = Ae

√

c x/ω

+ Be

−

√

c x/ω

for c > 0.

However, the boundary conditions eliminate both the linear and the exponential

solutions. Thus the constant −

is strictly positive, say γ

. The solutions are

X(x) = a cosγx + b sin γx.

Since X(0) = 0, this forces a = 0. And X(π) = 0 yields b sin γπ = 0. Thus

a nonzero solution is possible only if γ is an integer n. Therefore, the possible

solutions are

(x) = b sin nx for n ≥ 1.

Now return to the equation for T . Since c = −γ

= −n

, the DE for T

becomes

(t) + (nω)

T (t) = 0.

Again this has solutions

T (t) = A sin nωt + B cosnωt.

Putting these together, we obtain solutions for y(x, t) of the form

(x, t) = A

sinnx cos nωt + B

sinnx sin nωt for n ≥ 1.

The functions y

(x, t) correspond to the modes of vibration of the string. For

n = 1, we have a string shape of a single sinusoidal loop oscillating up and down.

This is the fundamental vibration mode of the string with the lowest frequency

ω. However, for n = 2, we obtain a function that has two “arches” that swing

back and forth. The frequency is twice the fundamental frequency. For general

n, we have higher frequency oscillations with frequency nω that oscillate n times

between the two ﬁxed endpoints at n times the rate. As we mentioned before, these

higher frequencies are called harmonics.

The differential equation (13.8.1) is linear, so linear combinations of solutions

are solutions. Thinking of solutions as waves, this combination of solutions is

called superposition; see Figure 13.4. Ignoring convergence questions, we have a

large family of possible solutions, all of the form

y(x, t) =

∞

n=1

sinnx cos nωt + B

sinnx sin nωt.

Now consider the initial condition (13.8.3). Substituting t = 0 into this, we arrive

at the boundary condition

f(x) = y(x, 0) =

∞

n=1

sinnx.

13.8 The Vibrating String (Formal Solution) 449

Likewise, allowing term-by-term differentiation with respect to t, we obtain

∂y

∂t

(x, t) =

∞

n=1

−nωA

sinnx sin nωt + nωB

sinnx cos nωt.

Substituting in the boundary condition at t = 0 yields g(x) =

∞

n=1

nωB

sinnx.

FIGURE 13.4. Superposition of two sine waves.

These are Fourier series. In fact, they are sine series because f and g are only

deﬁned on [0, π]. We have seen that summing them requires a certain amount of

delicacy. Notice that since the string is ﬁxed at 0 and π, the boundary functions

satisfy

f(0) = f(π) = g(0) = g(π) = 0.

Let us extend f and g to [−π, π] as odd functions by setting f (−x) = −f(x) and

g(−x) = −g(x). Then extend them to be 2π-periodic functions on the whole real

line. The values of the coefﬁcients A

and B

for n ≥ 1 are read off from the

Fourier (sine) coefﬁcients of f and g.

−π

f(t) sinnt dt =

f(t) sinnt dt

and

nωπ

−π

g(t) sinnt dt =

nωπ

g(t) sinnt dt

This form of the solution was proposed by Euler in 1748, and the same idea

was advanced by D. Bernoulli in 1753 and Lagrange in 1759. However, we want

to ﬁnd a closed form solution discovered by d’Alembert in 1747.

Returning to our proposed series solution, use the trig identity

2sinnx cos nωt = sin n(x + ωt) + sinn(x − ωt)

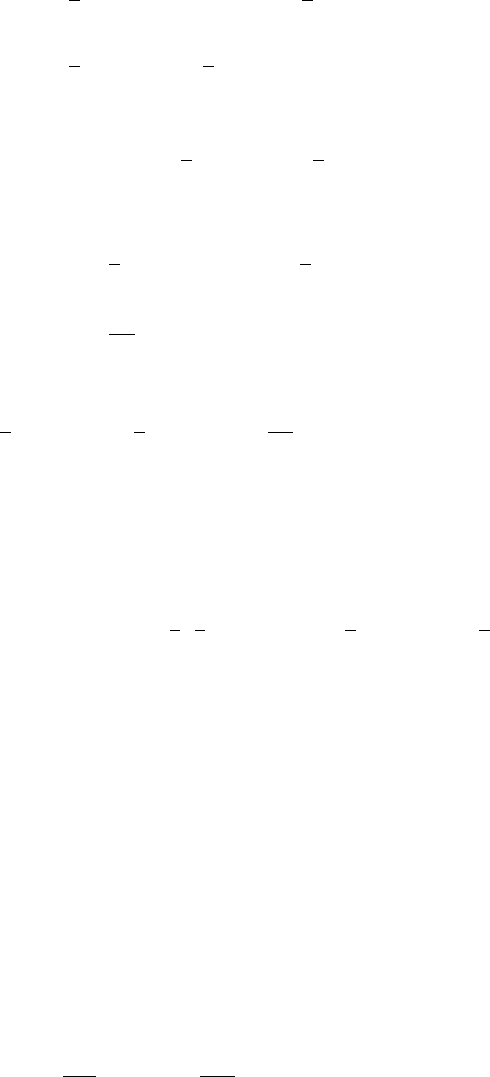
450 Fourier Series and Physics

and substitute into

∞

n=1

sinnx cos nωt =

∞

n=1

sinn(x + ωt) +

∞

n=1

sinn(x − ωt)

f(x + ωt) +

f(x − ωt).

Similarly,

∞

n=1

nωB

sinnx cos nωt =

g(x + ωt) +

g(x − ωt).

Thus

∞

n=1

sinnx sin nωt =

g(x + ωt) dt +

g(x − ωt) dt

2ω

x+ωt

x−ωt

g(s) ds.

Adding, we obtain the closed form solution

y(x, t) =

f(x + ωt) +

f(x − ωt) +

2ω

x+ωt

x−ωt

g(s) ds.

At this point, we have arrived at d’Alembert’s form of the solution. It is worth

noting that this form no longer involves a series and takes no notice of the method

we used to arrive here.

The role of ω becomes apparent in this formulation of the solution. Notice that

y(x, t) depends on the values of f and g only in the range [x − ωt, x + ωt]. We

should think of ω as the speed of propagation of the signal. In particular, if g = 0

and f is a small “bump” supported on [

+ ε], then for

≤ t ≤ 1 −

, the

function y(x, t) consists of two identical bumps moving out toward the ends of the

string at speed ω. When they reach the end, they bounce back. When the bumps

overlap, they are superimposed (added). But the shape of the bumps is not lost;

the message of the bump is transmitted accurately forever. In particular, the wave

equation for light has the constant c, the speed of light, in place of ω.

13.9. The Vibrating String (Rigorous Solution)

We may check directly that d’Alembert’s formula yields the solution to the

vibrating string problem without returning to the Fourier series expansion. Our

assumption that y satisﬁes a second-order PDE forces f to be C

and g to be C

We will consider more general initial data afterward.

13.9.1. THEOREM. Consider the vibrating string equation

∂

∂t

(x, t) = ω

∂

∂x

(x, t)

13.9 The Vibrating String (Rigorous Solution) 451

with initial conditions

y(x, 0) = f(x) and

∂y

∂t

(x, 0) = g(x)

such that f is C

and g is C

and f(0) = g(0) = f(π) = g(π) = 0. This has a

unique solution for all t > 0 given by

y(x, t) =

f(x + ωt) +

f(x − ωt) +

2ω

x+ωt

x−ωt

g(s) ds,

where f and g have been extended (uniquely) to the whole real line as 2π-periodic

odd functions.

PROOF. First, we verify that this is indeed a valid solution. Compute

∂y

∂x

(x, t) =

(x + ωt) +

(x − ωt) +

2ω

g(x + ωt) −

2ω

g(x − ωt)

∂

∂x

(x, t) =

(x + ωt) +

(x − ωt) +

2ω

(x + ωt) −

2ω

(x − ωt)

∂y

∂t

(x, t) =

(x + ωt) −

(x − ωt) +

g(x + ωt) +

g(x − ωt)

∂

∂t

(x, t) =

(x + ωt) +

(x − ωt) +

(x + ωt) −

(x − ωt).

Thus

∂

∂t

(x, t) = ω

∂

∂x

(x, t) and y(x, 0) = f (x) and

∂y

∂t

(x, 0) = g(x).

The question of uniqueness of solutions remains. As with the heat equation,

physical properties yield a clue. The argument in this case is based on conservation

of energy. Without actually justifying the physical interpretation, we introduce a

quantity called total energy obtained by adding the potential and kinetic energies

of the string:

E(t) = E(y, t) =

∂y

∂x

(x, t)

∂y

∂t

(x, t)

dx.

This is deﬁned for any solution y of our vibration problem. For convenience, we

switch to the notation y

, y

, and so on for partial derivatives. Use the Leibniz

Rule (8.3.4) to compute

(t) =

∂

∂t

(x, t)

(x, t) +

(x, t) dx.

Substitute y

= ω

(x, t) + 2y

(x, t) dx

∂

∂x

(x, t)

dx = y

(x, t)

x=π

x=0

= 0.

452 Fourier Series and Physics

The last equality follows since the string is ﬁxed at both endpoints, forcing the

relation y

(0, t) = y

(π, t) = 0. This shows that the energy is preserved (constant).

Now suppose that y

(x, t) is another solution to the wave problem. Then the

difference z(x, t) = y(x, t) − y

(x, t) is also a solution of the wave equation and

initial boundary conditions:

= ω

z(x, 0) = z

(x, 0) = 0.

It follows that z

(x, 0) = 0 too, and hence the energy of the system is

E =

(s, 0)

+ z

(s, 0)

ds = 0.

By conservation of energy, we deduce that

(s, t)

+ z

(s, t)

ds = 0 for all t ≥ 0.

In other words, z

(s, t) = z

(s, t) = 0 for all s and t. Therefore, z = 0, establish-

ing uniqueness. ¥

We know from real-world experience that a string may be bent into a non-C

shape. What happens then? In this case, we may approximate f uniformly by a

sequence of C

functions f

. Likewise, g may be approximated uniformly by a

sequence g

of C

functions. The wave equation with initial data y(x, 0) = f

(x)

and y

(x, 0) = g

(x) yields the solution

(x, t) =

(x + ωt) +

(x − ωt) +

2ω

x+ωt

x−ωt

(s) ds.

This sequence of solutions converges uniformly to

y(x, t) =

f(x + ωt) +

f(x − ωt) +

2ω

x+ωt

x−ωt

g(s) ds.

Thus, even though this function y may not be differentiable (so that it does not

make sense to plug y into our PDE), we obtain a reasonable solution to the wave

problem.

One very interesting aspect of this solution is the fact that y(x, t) is not any

smoother for large t than it is at time t = 0. Indeed, for every integer n ≥ 0,

y(x,

2nπ

) =

f(x + 2nπ) +

f(x − 2nπ) +

2ω

x+2nπ

x−2nπ

g(s) ds

= f (x).

This uses the fact that g has been extended to an odd 2π-periodic function and thus

g integrates to 0 over any interval of length (a multiple of) 2π. Similarly,

(x,

2nπ

) =

(x+2nπ) −

(x−2nπ) +

g(x+2nπ) +

g(x−2nπ)

= g(x).

Thus if the initial data f fails to be smooth at x

, this property persists along the

lines x(t) = x

±ωt. This is known as propagation of singularities. And because