Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

13.9 The Vibrating String (Rigorous Solution) 453

our solutions are odd 2π-periodic functions, these singularities recur within our

range. Following the solution only within the interval [0, π], these singularities

appear to reﬂect off the boundary and reenter the interval. This property is distinctly

different from the solution of the heat equation, which becomes C

∞

for t > 0 (see

Exercise 13.4.G) because the initial heat distribution gets averaged out over time.

The lack of averaging or damping in the wave equation is very important in real

life. It makes it possible to see, and to transmit radio and television signals over

long distances without signiﬁcant distortion.

The Fourier series approach still has more to tell us. The Fourier coefﬁcients in

the expansion of the solution y(x, t) decompose the wave into a sum of harmonics

of order n for n ≥ 1. In fact, the term

(x, t) = A

sinnx cos nωt + B

sinnx sin nωt

may be rewritten as

(x, t) = C

sinnx sin(nωt + τ

where C

+ B

and the phase shift τ

is chosen so that sinτ

= A

and cosτ

= B

. Thus as t increases, y

modulates through multiples of

sinnx from C

down to −C

and back.

The combination of different harmonics gives a wave its shape. In electrical

engineering, one often attempts to break down a wave into its component parts or

build a new wave by putting harmonics together. This amounts to ﬁnding a Fourier

series whose sum is a speciﬁed function. That is the problem we will investigate

further in the next chapter.

Exercises for Section 13.9

A. Using the series for y(x, t) and the orthogonality relations, show that

E =

(x)

2ω

g(x)

dx =

∞

n=1

(|A

+ |B

B. Consider a guitar string that is plucked in the centre to a height h starting at rest.

Assume that the initial position is piecewise linear with a sharp cusp in the centre.

(a) What is the odd 2π-periodic extension of the initial position function f? Sketch it.

(b) Plot the graph of the solution y(x, t) for t = 0,

3ω

2ω

2π

(d) Compute the energy for this string.

C. Verify that A

sinnx cosnωt + B

sinnx sinnωt = C

sinnx sin(nωt + τ

), where

+ B

and τ

is chosen so that sinτ

= A

and cosτ

= B

D. Let F and G be C

functions on the line.

(a) Show that y(x, t) = F(x + ωt) + G(x − ωt) for x ∈ R and t ≥ 0 is a solution of

the wave equation the whole line.

(b) What is the initial position f and velocity g in terms of F and G?

Express F and G in terms of f and g.

[x − ωt, x + ωt].

454 Fourier Series and Physics

(d) Explain the physical signiﬁcance of part (c) in terms of the speed of propagation of

the signal.

E. Consider the wave equation on R. Let u = x + ωt and v = x − ωt.

(a) Show that

∂

∂u

∂

∂x

2ω

∂

∂t

and

∂

∂v

∂

∂x

−

2ω

∂

∂t

Hence deduce that after a change of variables, the wave equation becomes

∂

∂u

∂

∂v

y = 0.

(b) Hence show that every solution has the form y = F (u) + G(v).

unique solution on the line.

F. Let w(x) be a strictly positive function on [0, 1], and consider the PDE deﬁned for

0 ≤ x ≤ 1 and t ≥ 0:

∂

∂t

(x, t) = w(x)

∂

∂x

(x, t) + H(x, t)

y(x, 0) = f(x) y

(x, 0) = g(x)

and y(0, t) = y(1, t) = 0. Suppose that y(x, t) and z(x, t) are two solutions, and let

u = y − z. Consider the quantity

E(t) =

(x, t) +

(x, t)

w(x)

dx.

Show that E is the zero function, and hence deduce that the solution of the PDE is

unique.

13.10. Appendix: The Complex Exponential

Our goal in this section is to extend the deﬁnition of the exponential function

to all complex numbers. Although we quickly review the basic ideas of complex

numbers C, prior experience with complex numbers will be quite helpful.

Complex numbers may be written uniquely as a + ib for a, b ∈ R. Addition is

just given by the rule

(a + ib) + (c + id) = (a + c) + i(b + d).

Multiplication uses distributivity and the rule i

= −1. So

(a + ib)(c + id) = (ac − bd) + i(ad + bc).

The conjugate of a complex number z = a + ib is the number

z := a − ib. The

absolute value or modulus is given by

|z| = (zz)

1/2

+ b

The set of all complex numbers is closed under addition and subtraction, multipli-

cation and division by nonzero elements. In particular, if z = a + ib 6= 0, then

a − ib

+ b

+ i

−b

+ b

13.10 Appendix: The Complex Exponential 455

This makes C into a ﬁeld containing the reals as a proper subset. We also deﬁne

the real part and imaginary part of a complex number by

Re(a + ib) = a and Im(a + ib) = b.

Note that the imaginary part is a real number.

One crucial property of C is that it is an algebraically closed ﬁeld, mean-

ing that every polynomial with complex coefﬁcients factors as a product of degree

one polynomials. This result is called the Fundamental Theorem of Algebra,

although modern algebra does not accord C the preeminent role that it had in the

nineteenth century, when the theorem was named.

The analysis of complex functions has a lot of interesting aspects. Functions

of a complex variable that are differentiable are called analytic, and they have

many amazing properties. These properties are developed in complex analysis, an

important subject that is often quite different from real analysis.

To extend the deﬁnition of the exponential function to all complex numbers,

we must construct a differentiable function E : C → C such that E(w + z) =

E(w)E(z) for all w and z in C and so that E(x) = e

for all x ∈ R. Once we have

established the existence of this function, we will write e

for E(z).

Let us calculate some simple properties that such a function must have. First,

E(x + iy) = e

E(iy).

Using the differentiability, we get

(z) = lim

h→0

E(z + h) − E(z)

= E(z) lim

h→0

E(h) − E(0)

= E(z) lim

x→0

− 1

= E(z).

Now concentrate on the function f (y) = E(iy). Split it into its real and imag-

inary parts as f(y) = E(iy) = A(y) + iB(y). Differentiating with respect to y

yields

(y) = A

(y) + iB

(y)

= E

(iy)

d(iy)

= iE(iy) = −B(y) + iA(y)

So we arrive at the system of differential equations

(y) =−B(y)

(y) = A(y).

This leads to the second-order differential equation A

(y) = −A(y). From the

identity 1 = E(0) = A(0) + iB(0), we also get the initial conditions A(0) = 1

and A

(0) = −B(0) = 0. We have seen that this system has a unique solution

A(y) = cosy and B(y) = siny.

456 Fourier Series and Physics

Thus we arrive at a unique solution E(iy) = cosy + i siny. So

E(x + iy) = e

cosy + i siny

13.10.1. THEOREM. The function E(x + iy) = e

cosy + i siny

satisﬁes

the identities E(z + w) = E(z)E(w) for all complex numbers z, w. Moreover, E

is differentiable and E

(z) = E(z) for all z ∈ C.

PROOF. Notice that

E(iy)E(iv) =

cosy + i siny

¢¡

cosv + i sinv

cosy cosv − siny sinv

+ i

cosy sinv + siny cosv

= cos(y + v) + i sin(y + v) = E(iy + iv).

Hence

E(x + iy)E(u + iv) = e

cos(y) + i sin(y)

cos(v) + i sin(v)

= e

x+u

E(iy + iv) = E((x + iy) + (u + iv)).

So E satisﬁes the multiplicative property.

The derivative property is a bit more delicate. The hard part is to show that

(0) = 1. For then, as on the previous page, we obtain

(z) = E(z)E

(0) = E(z).

To verify that E

(0) = 1, we must show that

0 = lim

h→0

E(h) − 1

− 1

= lim

h→0

|E(h) − 1 − h|

|h|

The complication comes from the fact that h can be a small complex number, not

just a real number, as it approaches 0. However, we need only facts from the

calculus of real functions to verify this limit. The major tool for making estimates

is the Mean Value Theorem. Let us write h = x + iy. We may assume that

|h|

= x

+ y

< 1. In particular, |x| < 1. Calculate

E(h) − 1 − h = e

cosy + ie

siny − 1 − x − iy

= e

(cosy − 1) + (e

− 1 − x) + ie

(siny − y) + iy(e

− 1).

Each of these terms can be estimated by the Mean Value Theorem. First, since

f(y) = cos y has derivative f

(y) = −siny, it follows that there is a value c

between 0 and y such that

|cosy − 1| = | − sinc||y| ≤ |c||y| ≤ |y|

So e

|cosy − 1| ≤ e|y|

≤ e|h|

provided that |x| ≤ 1.

A similar treatment of the function e

shows that

− 1| ≤ e|x| for all |x| ≤ 1.

Now repeat the argument for the function g(x) = e

−1 −x, which has derivative

(x) = e

− 1. Again by the Mean Value Theorem, there is a point c between 0

13.10 Appendix: The Complex Exponential 457

and x so that

− 1 − x| = |e

− 1||x| ≤ e|c||x| ≤ e|h|

A third application of the Mean Value Theorem with k(y) = siny − y and

derivative k

(y) = cosy − 1 yields a point c between 0 and y so that

|siny − y| = |y||cosc − 1| ≤ |y||c|

≤ |y|

Together with the inequality |e

| ≤ e for |x| ≤ 1, this yields

|ie

(siny − y)| ≤ e|y|

≤ e|h|

Finally, the fourth term is handled by 2|xy| ≤ x

+ y

= |h|

, so

|y(e

− 1)| ≤ e|y||x| ≤ 2|h|

Putting it all together yields, for |h| ≤ 1,

|E(h) − 1 − h| = e

cosy−1

−1−x

(siny−y)

iy(e

−1)

≤ e|h|

+ e|h|

+ 2|h|

2e + 2 + e|h|

|h|

Thus

lim

h→0

|E(h) − 1 − h|

|h|

= 0.

From now on, we will write e

instead of E(z), as this theorem justiﬁes calling

it the exponential function. If z = a + ib is any complex number, let r = |z| =

√

+ b

. Then z/r = a/r + ib/r has modulus 1 and hence lies on the unit circle.

Therefore there is an angle θ, which is unique up to a multiple of 2π, such that

z/r = cos θ + i sinθ = e

iθ

. So z = re

iθ

. This is called the polar form since z is

represented as (r, θ) in the polar coordinates of the plane.

The relationship between e

±ix

and sinx and cosx is important in Fourier se-

ries. In particular, we have

cosnx = Re

inx

+ e

−inx

and

sinnx = Im

inx

− e

−inx

We record some of the facts and ask you to prove them in the Exercises.

Since the pairs {cosnx, sinnx} and {e

inx

, e

−inx

} both span the same two-

dimensional space (using complex coefﬁcients), it follows that a Fourier series may

be written as

(13.10.2) f(θ) ∼

∞

n=−∞

inθ

where the coefﬁcients are given by

(13.10.3) a

2π

−π

f(θ)e

−inθ

dθ.

458 Fourier Series and Physics

We have already seen that we could sum the Poisson kernel by using complex

exponentials and the formula for summing geometric series. This idea has many

applications in Fourier series. We give another example.

We beginwith a lemma that can be proved using trig identities butis transparent

using complex exponentials.

13.10.4. LEMMA.

(θ) :=

k=1

sinkθ =

cosθ/2 − cos(n +

)θ

2sinθ/2

for θ 6= 2mπ

In particular, |S

(θ)| ≤ πε

−1

uniformly on [ε, 2π − ε] for all n ≥ 1.

PROOF. We use the exponential formula for sinkx and the formula for summing a

geometric series. Compute

k=1

sinkθ =

k=1

ikθ

−

k=1

−ikθ

i(n+1)θ

− e

iθ

2i(e

iθ

− 1)

−

−i(n+1)θ

− e

−iθ

2i(e

−iθ

− 1)

i(n+1/2)θ

+ e

−i(n+1/2)θ

− e

iθ/2

− e

−iθ/2

2i(e

iθ/2

− e

−iθ/2

)

iθ/2

+ e

−iθ/2

−

i(n+1/2)θ

+ e

−i(n+1/2)θ

iθ/2

− e

−iθ/2

cosθ/2 − cos(n +

)θ

2sinθ/2

If ε ≤ θ ≤ 2π − ε, then

|2sinθ/2| ≥ |2 sin ε/2| ≥ 2

2ε

It follows that in this interval,

(θ)| ≤

2ε/π

13.10.5. EXAMPLE. A Fourier series that has positive coefﬁcients decreasing

monotonically to 0 always converges to a function that is continuous on (0, 2π) but

may have a discontinuity at multiples of 2π. The key tool is Dirichlet’s Test (3.4.10)

for the convergence of a sequence. We will examine this in a speciﬁc instance.

Consider the Fourier sine series

f(θ) =

∞

k=1

sinkθ.

13.10 Appendix: The Complex Exponential 459

Notice that

−

k + 1

−

k + 2

+ ··· +

n − 1

−

n−1

j=k

j(j + 1)

Following the proof of the Dirichlet Test (3.4.10), we can rearrange the partial sums

of the sine series as

k=1

sinkθ =

k=1

n−1

j=k

j(j + 1)

sinkθ

n−1

j=1

j(j + 1)

(θ) +

(θ).

On the interval [ε, 2π − ε], we have the bounds

sup

ε≤θ≤2π−ε

j(j + 1)

(θ)

≤

j(j + 1)ε

So we can apply the Weierstrass M-test. We have a telescoping sum:

∞

j=1

j(j + 1)ε

∞

j=1

−

j + 1

< ∞.

So the series

∞

j=1

j(j+1)

(θ) converges uniformly on [ε, 2π −ε]. Since the uniform

limit of continuous functions is continuous by Theorem 8.2.1, the sum is a continu-

ous function on [ε, 2π −ε] for any ε > 0. Hence the limit exists and is a continuous

function f(θ) on (0, 2π).

Therefore, the partial sums also converge:

lim

n→∞

k=1

sinkθ = lim

n→∞

n−1

j=1

j(j + 1)

(θ) + lim

n→∞

(θ)

= f (θ).

The second limit is 0 since

sup

ε≤θ≤2π−ε

(θ)

≤

nε

This tends to 0 uniformly on [ε, 2π − ε] as n tends to inﬁnity.

Now let us attempt to compute f (θ). It is convenient to work with the harmonic

extension

u(r, θ) =

∞

k=1

sinnθ

460 Fourier Series and Physics

as in Section 13.4 because better convergence is obtained inside the disk. Take the

partial derivative with respect to r, and sum the resulting geometric series.

(r, θ) =

∞

k=1

n−1

sinnθ

∞

k=1

n−1

inθ

∞

k=1

n−1

−inθ

iθ

2i(1 − re

iθ

)

−iθ

2i(1 − re

−iθ

)

It is not difﬁcult to integrate this function with respect to r from (0, θ) to (R, θ)

using the initial condition u(0, θ) = A

= 0 to obtain

u(R, θ) =

log(1 − Re

iθ

) −

log(1 − Re

−iθ

)

log

1 − Re

iθ

1 − Re

−iθ

Notice that 1 − re

−iθ

is the complex conjugate of 1 − re

iθ

. Thus if we write

1 − re

iθ

= se

iα

, then

u(r, θ) =

log

iα

−iα

loge

2iα

= −α.

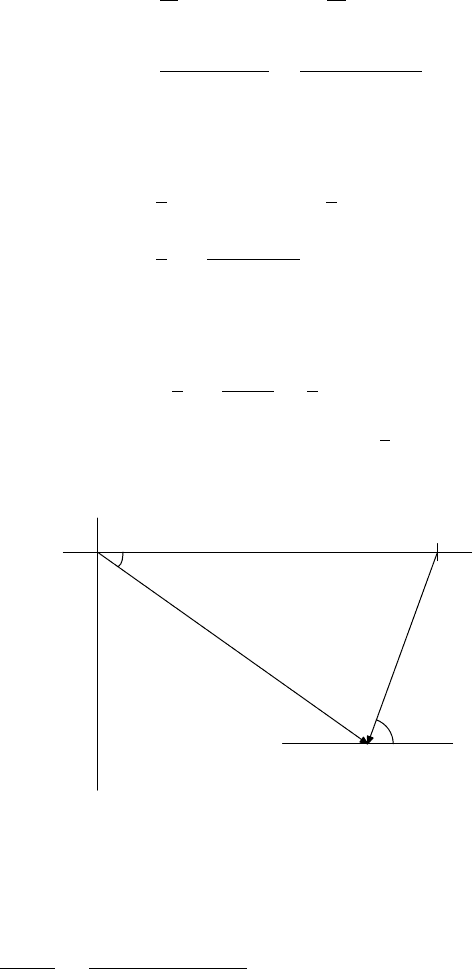
Look at Figure 13.5. For θ in (0, π), α belongs to (−

, 0), and it reverses sign on

(π, 2π). So u(r, θ) > 0 for θ in (0, π), and it is negative for θ in (π, 2π).

iα

−re

iθ

FIGURE 13.5. The vector se

iα

= 1 − re

iθ

We have a triangle in Figure 13.5 with angle |α| opposite the side of length r

and angle π −|α|−|θ| opposite the side of length 1. By the law of sines, we obtain

sin|α|

sin(π − |α| − |θ|)

= sin |α|cos|θ| + cos|α|sin |θ|.

13.10 Appendix: The Complex Exponential 461

Solving, we obtain

tan|α| =

r sin|θ|

1 − r cosθ

Using the information about the sign of u, we obtain

u(r, θ) = Tan

−1

r sinθ

1 − r cosθ

This deﬁnition of u makes sense provided that the denominator 1 − r cosθ is

not 0, which happens on the closed unit disk except for one boundary point (1, 0).

Hence u(r, θ) is deﬁned and continuous on

D \ {(1, 0)}. In particular, using trig

formulas, we obtain

f(θ) = u(1, θ) = Tan

−1

sinθ

1 − cos θ

= Tan

−1

2sin(θ/2) cos(θ/2)

2sin

(θ/2)

= Tan

−1

cot

π − θ

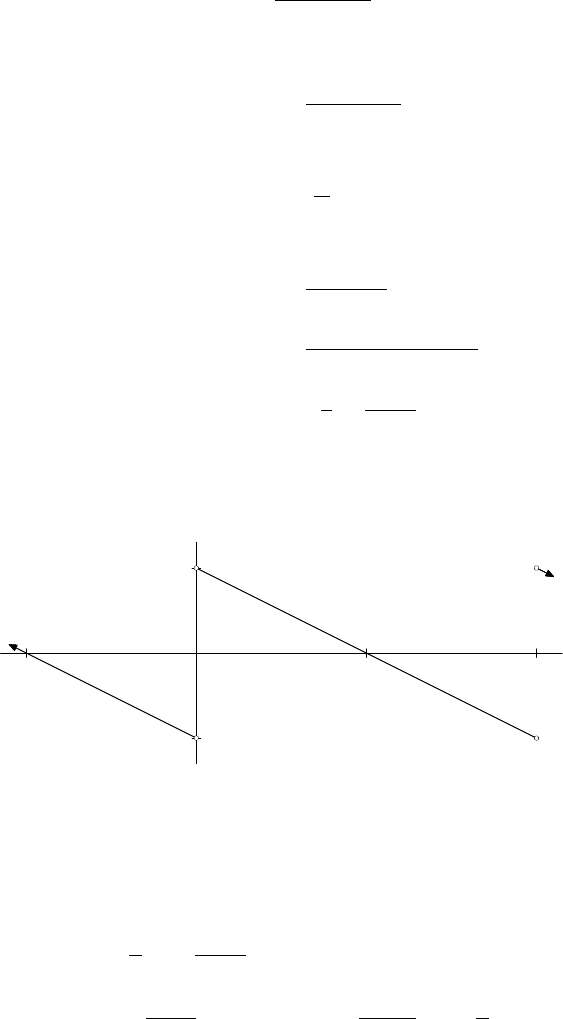
Note that this is valid for θ in (0, 2π), not our usual (−π, π) interval. For the graph

of f, see Figure 13.6.

−π

2π

π/2

−π/2

FIGURE 13.6. The graph of f as a 2π-periodic function on R.

As a ﬁnal check, we compute the Fourier series of f. This is an odd function,

so it has a sine series. Use integration by parts:

2π

π − θ

sinnθ dθ

= −

π − θ

2nπ

cosnθ

2π

−

2π

cosnθ

2nπ

dθ =

462 Fourier Series and Physics

Exercises for Section 13.10

A. (a) Graph the image of a line parallel to the y-axis under the exponential map.

(b) Graph the image of a line parallel to the x-axis under the exponential map.

function one-to-one and onto the whole complex plane except for the point 0.

B. (a) Express f(θ) = A

cosnθ + B

sinnθ as a linear combination of e

inθ

and e

−inθ

(b) Show that the coefﬁcients are given by the formula (13.10.3).

the form (13.10.2).

C. Find a formula for the sum

k=1

coskθ.

D. Deﬁne the complex Fourier series of an absolutely integrable 2π-periodic function

f(θ) by f ∼

∞

n=−∞

inθ

, where c

2π

−π

f(θ)e

−inθ

dθ.

(a) Find the relationship between {A

, B

} and {c

, c

−k

(b) Hence show that

k=−n

ikθ

= A

k=1

coskθ + B

sinkθ.

inθ

: n ∈ Z} is an orthonormal set in L

(−π, π).

E. Sum the Fourier series

∞

n=0

−n

cosnθ and

∞

n=1

−n

sinnθ.

HINT: Take the real and imaginary parts of

∞

n=0

−n

inθ

F. Show that

∞

k=1

coskθ converges uniformly on [ε, 2π − ε] for ε > 0.

G. Deﬁne cosz = (e

+ e

−iz

)/2 and sinz = (e

− e

−iz

)/2i for all z ∈ C.

(a) Prove that sin(w + z) = sinw cosz + cosw sin z.

(b) Find all solutions of sin z = 2.