Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

6.1 Differentiable Functions 143

PROOF. First we compute the limit by substituting h = x − x

lim

x→x

f(x) − T (x)

x − x

= lim

h→0

f(x

+ h) −

f(x

) + f

= lim

h→0

f(x

+ h) − f(x

)

− f

) = 0.

Now if another linear function L(x) satisﬁes this limit, then by the continuity

of L and f , we have

f(x

) − L(x

) = lim

x→x

f(x) − L(x)

= lim

x→x

(x − x

)

f(x) − L(x)

x − x

= 0.

So L(x) = f (x

) + m(x − x

), where m is its slope, and

m = L

) = lim

h→0

L(x

+ h) − L(x

)

= lim

h→0

L(x

+ h) − f(x

+ h)

f(x

+ h) − f(x

)

= 0 + f

) = f

Thus the line L goes through the point (x

, f(x

)) and has the same slope as T .

Consequently, L = T . ¥

An immediate consequence is that the tangent line is a good approximant to f

near x

in the sense of (2) in Corollary 6.1.4.

6.1.4. COROLLARY. If f(x) is a function on (a, b) and x

∈ (a, b), then the

following are equivalent:

(1) f is differentiable at x

(2) There is a linear function T (x) and a function ε(x) on (a, b) such that

lim

x→x

ε(x) = 0 and f (x) = T (x) + ε(x)(x − x

(3) There is a function ϕ(x) on (a, b) such that f (x) = f(x

) + ϕ(x)(x −x

)

and lim

x→x

ϕ(x) exists.

If these hold, then the linear function T (x) in (2) is the tangent line, and the limit

lim

x→x

ϕ(x) in (3) equals f

PROOF. Clearly, we must deﬁne ε(x) =

f(x) − T (x)

x − x

and ϕ(x) =

f(x) − f(x

)

x − x

for x 6= x

. Lemma 6.1.3 shows that (1) and (2) are equivalent and that the linear

function T is necessarily the tangent line T (x) = f (x

) + f

)(x − x

). Thus

if (2) holds, then ϕ(x) = f

) + ε(x) satisﬁes f(x) = f(x

) + ϕ(x)(x − x

)

and lim

x→x

ϕ(x) = f

). So (3) holds and limit equals f

). Conversely, if (3)

144 Differentiation and Integration

holds, then let L = lim

x→x

ϕ(x). It is easy to check that T (x) = f(x

) + L(x − x

)

and ε(x) = ϕ(x) − L satisfy (2). ¥

6.1.5. REMARK. It is easy to describe continuous functions that are not differ-

entiable at every point. The prototypical example is f(x) = |x|. This function is

differentiable at every point except x = 0. Here it has left and right derivatives −1

and 1, respectively. As this function comes to a point at the origin, it is intuitively

clear that no straight line is a good approximant near x = 0.

A more subtle example is g(x) =

√

x, graphed in Figure 6.2 This has derivative

(x) =

−2/3

for all x 6= 0. But at x = 0, we have

lim

h→0

g(h) − g(0)

= lim

h→0

−2/3

= +∞.

So this function is not differentiable because it has a vertical tangent at the origin.

y =

√

FIGURE 6.2. The graph of

√

y =

|x|

FIGURE 6.3. The graph of

|x|.

A related example is the function h(x) =

|x|, graphed in Figure 6.3. This

function has a cusp, with right derivative +∞ and left derivative −∞.

6.1 Differentiable Functions 145

Looking only at these examples, it is intuitively plausible that a continuous

function has to be differentiable at “most” points, but this is not true. These func-

tions do not give the full extent of nasty behaviour. There are continuous functions

that are not differentiable at any point! We will construct such a function in Exam-

ple 8.4.9. Unsurprisingly, this function is not given by a simple formula, but rather

is expressed as a convergent inﬁnite series of functions. In spite of the difﬁculties

in writing down such functions, there are actually many of them, in a certain sense;

see Proposition 9.3.3.

The linearity of differentiation [i.e., that (αf + βg)

= αf

+ βg

for functions

f and g and scalars α and β] follows from the linearity of limits. The product and

quotient rules require more care; they are left as exercises with hints. However, the

chain rule is yet more subtle.

6.1.6. THE CHAIN RULE.

Suppose that f is deﬁned on [a, b] and has range contained in [c, d]. Let g be deﬁned

on [c, d]. Suppose that f is differentiable at x

∈ [a, b] and g is differentiable at

f(x

). Then the composition h(x) = g(f (x)) is deﬁned, and

) = g

(f(x

))f

PROOF. Using part (3) of Corollary 6.1.4, write f(x) = f(x

) + ϕ(x)(x − x

where lim

x→x

ϕ(x) = f

). Similarly, g(y) = g(f(x

)) + ψ(y)(y −f(x

)), where

lim

y→f(x

)

ψ(y) = g

(f(x

)). Then

h(x) = g(f(x)) = g(f(x

)) + ψ(f(x))(f(x) − f (x

))

= g(f(x

)) + ψ(f(x))ϕ(x)(x − x

)

and by Corollary 6.1.4,

lim

x→x

ψ(f(x))ϕ(x) = g

(f(x

))f

By Corollary 6.1.4, h is differentiable at x

and h

) = g

(f(x

))f

). ¥

6.1.7. EXAMPLE. There are functions that are differentiable but do not have

a continuous derivative. Let a > 0 and consider f (x) = x

sin(1/x) for x > 0

and set f(0) = 0. This is evidently continuous at every point except possibly 0.

However, since |sin(1/x)| ≤ 1 and lim

x→0

= 0, the Squeeze Theorem shows that

f is also continuous at x = 0.

Consider the derivative of f. For x > 0, we invoke the product and chain rules

to compute

(x) = ax

a−1

sin(1/x) − x

a−2

cos(1/x).

The point x = 0 must be handled separately using the deﬁnition of derivative.

(0) = lim

h→0

sin(1/h)

= lim

h→0

a−1

sin(1/h)

146 Differentiation and Integration

If a > 1, the Squeeze Theorem yields f

(0) = 0; while for a ≤ 1, the values of

a−1

sin(1/h) oscillate wildly between large positive and negative values, and the

limit does not exist.

So for 0 < a ≤ 1, f is continuous but not differentiable at x = 0. A key point

of interest is the values 1 < a ≤ 2. For these values, f(x) is differentiable at every

point but the derivative f

(x) is not continuous at x = 0. Thus a function may be

differentiable but not C

Exercises for Section 6.1

A. Prove that (αf + βg)

) = αf

) + βg

) for all functions f and g on [a, b] that

are differentiable at x

B. If f is differentiable at x

and a ∈ R, show that lim

h→0

f(x

+ ah) − f(x

)

= af

C. Explain what goes wrong with the proof of Proposition 6.1.2 if f is not differentiable.

D. Let f and g be differentiable functions on (a, b). Suppose there is a point x

in (a, b)

with f(x

) = g(x

) and f(x) ≤ g(x) for a < x < b. Prove that f

) = g

E. Show that the derivative of an even function is odd, and the derivative of an odd

function is even. Recall that a function f is even if f(−x) = f(x) and is odd if

f(−x) = −f(x).

F. Prove the product rule: (f g)

) = f

)g(x

) + f(x

) for all functions f

and g on [a, b] that are differentiable at x

HINT: Express f (x

+ h)g(x

+ h) − f(x

)g(x

) as

f(x

+ h) − f(x

)

g(x

+ h) + f(x

)

g(x

+ h) − g(x

)

G. For each positive integer n, give an example of a function which is C

but not C

n+1

HINT: Look at Example 6.1.7.

H. Prove the quotient rule: (f/g)

) =

)g(x

) − f(x

)

g(x

)

for all functions f

and g on [a, b] that are differentiable at x

and g(x

) 6= 0.

HINT: Let h = f /g and use the product rule on f = gh. Solve for h

I. Suppose that f is a continuous, one-to-one function from the interval [a, b] onto [c, d].

By Theorem 5.7.6, the inverse function f

−1

(x) is also continuous. Prove that if

f(x

) = y

and f

) 6= 0, then (f

−1

)

) =

)

−1

))

HINT: Use Theorem 6.1.4(3) to establish that f

−1

(y)−f

−1

) =

ϕ(f

−1

(y))

(y−y

J. We say f is right-differentiable at x

if lim

h→0

[f(x

+ h) − f(x

)]/h exists. In this

case, the value is denoted f

+).

(a) Deﬁne left-differentiable at x

and assign a meaning to f

−).

(b) Show that f is differentiable at x

if and only if it is both left-differentiable and

right-differentiable at x

and f

+) = f

−).

K. Find left and right derivatives of f(x) =

√

1 − sinx at every point. Where does f fail

to be differentiable?

6.1 Differentiable Functions 147

L. Suppose f : [a, b] → R is differentiable on (a, b) and continuous on [a, b]. Does it

follow that f is right-differentiable at a and left-differentiable at b?

M. Some calculus text books write “(f

−1

)

”. Find several things wrong with this

statement. Which error is the most egregious?

N. The function sinx is 2π-periodic and consequently is deﬁnitely not one-to-one.

(a) How do we deﬁne the inverse function arcsiny?

(b) How does the choice you make in part (a) affect the graph of arcsin y? What is the

effect on the derivative?

O. If f is periodic with period T , show that f

is also T -periodic.

P. Recall that we said a function f(x) is asymptotic to a curve c(x) as x tends to +∞ if

lim

x→+∞

|f(x) − c(x)| = 0.

(a) Show that if f (x) is asymptotic to a line L(x) = ax + b as x tends to +∞, then

a = lim

x→+∞

f(x)

and b = lim

x→+∞

f(x) − ax. (As usual, this includes showing that

the limits exist.)

(b) Find all of the asymptotes (including horizontal and vertical ones) for

f(x) =

(x − 2)

(x + 1)

. Sketch the graph.

Q. Sketch the curve f(x) = xe

−

for x 6= 0. Pay attention to the following:

(a) asymptotic behaviour at ±∞

(b) ﬁnd all critical points

at 0

(d) points of inﬂection

R. Sketch the curve f(x) =

(logx)

+ 4log x

(1 + logx)

for x > 0. Pay attention to the following:

(a) points where f is zero or undeﬁned

(b) limits of f and f

at 0

(d) Indicate all points of inﬂection on the graph, but do not compute the second deriv-

ative to compute them exactly

S. Suppose that f is continuous on (a, b).

(a) Show that f is differentiable at x

∈ (a, b) if and only if lim

x→x

y→x

−

f(x) − f(y)

x − y

exists.

(b) Why is part (a) false without the continuity hypothesis?

T. Establish the Leibniz formula that the nth derivative of a product f(x)g(x) is given by

k=0

(k)

(x)g

(n−k)

(x). HINT: Use induction.

U. (a) Suppose that g is continuous at x = 0. Prove that f(x) = xg(x) is differentiable at

x = 0.

(b) Conversely, suppose that f(0) = 0 and f is differentiable at x = 0. Prove that

there is a function g that is continuous at x = 0 and satisﬁes f(x) = xg(x).

148 Differentiation and Integration

6.2. The Mean Value Theorem

The Mean Value Theorem is the fundamental approximation result of differ-

ential calculus. It is endlessly applied and, indeed, is the most useful analytic tool

that calculus provides. However, the proof depends on the Extreme Value Theo-

rem, putting a valid proof beyond many calculus courses. We devote this section to

proving the Mean Value Theorem.

The starting point is the following basic result on which all of calculus relies—

the location of possible extrema. Simply stated, it says that extrema of continuous

functions occur at the endpoints or at critical points, where the derivative is either

undeﬁned or equal to 0. Sometimes this result is credited to Fermat.

6.2.1. FERMAT’S THEOREM.

Let f be a continuous function on an interval [a, b] that takes its maximum or min-

imum value at a point x

. Then

(1) x

is an endpoint a or b, or

(2) f is not differentiable at x

, or

(3) f is differentiable at x

and f

) = 0.

PROOF. Suppose that the ﬁrst two options do not apply. Then x

is an interior point

at which f is differentiable. For convenience, assume that x

is a maximum. Since

f(x

+ h) − f(x

) ≤ 0, the limit from the right yields

) = lim

h→0

f(x

+ h) − f(x

)

≤ 0

and the limit from the left yields

) = lim

h→0

−

f(x

+ h) − f(x

)

≥ 0.

Hence f

) = 0. ¥

Next, we prove a special case of Mean Value Theorem, traditionally called

Rolle’s Theorem, which we can then use to deduce the general case.

6.2.2. ROLLE’S THEOREM.

Suppose that f is a function that is continuous on [a, b] and differentiable on (a, b)

such that f(a) = f(b) = 0. Then there is a point c ∈ (a, b) such that f

PROOF. If the maximum value and minimum value of f are both 0, then f is

constant and f

greater than 0, or the minimum is less. For convenience, assume the former.

By the Extreme Value Theorem (Theorem 5.4.4), there is a point c at which

f attains its maximum value. Evidently, c is an interior point. So by Fermat’s

Theorem, we have f

6.2 The Mean Value Theorem 149

6.2.3. EXAMPLE. Differentiability is necessary at every interior point for this

theorem to be valid. For example, the continuous function on [−1, 1] given by

f(x) = 1−|x| does not have any point at which f

(x) = 0. Here f is differentiable

at every point except the point x = 0 at which the maximum occurs.

Now a rescaling trick yields the general result. Actually, this idea can used to

solve other problems as well, so perhaps we should call it a method.

6.2.4. MEAN VALUE THEOREM.

Suppose that f is a function that is continuous on [a, b] and differentiable on (a, b).

Then there is a point c ∈ (a, b) such that

f(b) − f(a)

b − a

Before proving the theorem, it is worth pointing out its signiﬁcance. The key

point is that we have a connection between the derivative of the function and its

average slope. It is this connection that allows us to deduce properties of f from

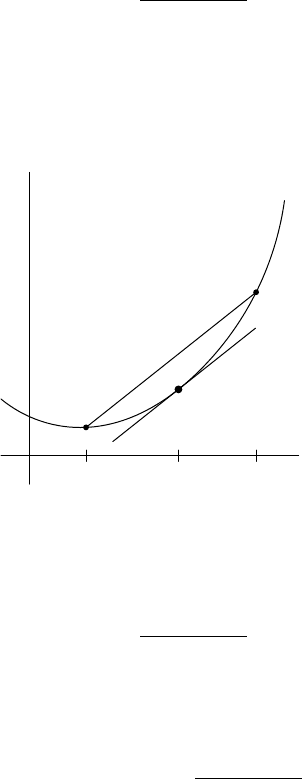
properties of its derivative. Figure 6.4 shows the theorem graphically.

a bc

FIGURE 6.4. Graph for the Mean Value Theorem.

PROOF. Let L(x) be the linear function through (a, f(a)) and (b, f(b)), namely

L(x) = f (a) +

f(b) − f(a)

b − a

(x − a).

Consider the function g(x) = f(x) − L(x). Then g is continuous on [a, b] and

differentiable on [a, b] since f and L are. Moreover, g(a) = g(b) = 0. So by

Rolle’s Theorem, there is a point c ∈ (a, b) at which

0 = g

f(b) − f(a)

b − a

This is the desired point. ¥

150 Differentiation and Integration

The ﬁrst important consequence is used repeatedly in calculus arguments.

6.2.5. COROLLARY. Let f be a differentiable function on [a, b].

(1) If f

(x) is (strictly) positive, then f is (strictly) increasing.

(2) If f

(x) is (strictly) negative, then f is (strictly) decreasing.

(3) If f

(x) = 0 at every x ∈ (a, b), then f is constant.

PROOF. For any a ≤ x < y ≤ b, apply the Mean Value Theorem on [x, y] to obtain

a point c in between so that

f(y) − f(x) = f

(c)(y − x) ≥ 0.

So f is increasing. If f

> 0, then the same argument yields a strict inequality.

Likewise, the decreasing case follows. A function that is both increasing and de-

creasing at the same time is constant. ¥

6.2.6. EXAMPLE. We show how the Mean Value Theorem may be used to

obtain useful approximations.

Consider f (x) = sinx on [0,

]. For any x ∈ (0,

], we may apply the Mean

Value Theorem on [0, x] and ﬁnd a point c with 0 < c < x such that

f(x) − f(0)

x − 0

sinx

= f

Thus we obtain the well-known inequality sinx < x for 0 < x ≤

. It is evidently

valid for x >

as well.

Now consider g(x) = 1 − x

/2 − cosx. Applying the Mean Value Theorem

again, we obtain a (different) point c so that

g(x) − g(0)

x − 0

1 − x

/2 − cos x

= g

cosx > 1 −

for 0 < x ≤

Then consider the function h(x) = sinx − x + x

/6. Once again, apply the

Mean Value Theorem on [0, x] with 0 < x ≤ π/2:

sinx − x + x

= h

> 0.

Hence

x −

< sin x < x on (0, π/2].

A fourth application using k(x) = 1 − x

/2 + x

/24 − cos x yields

1 − x

/2 + x

/24 − cos x

= k

/6) > 0.

6.2 The Mean Value Theorem 151

Thus

1 −

< cosx < 1 −

on (0, π/2].

These approximations are reasonably good when x is near zero. They are not

much use for x away from zero. If you were interested in approximating cosx near

x = π/4, you would begin with a = π/4 rather than 0.

Many functions that occur in practice can be differentiated several times. We

deﬁne the higher-order derivatives recursively by f

(n+1)

(x) =

(n)

(x), assum-

ing that f

(n)

turns out to be differentiable.

It stands to reason that information about higher order derivatives should add

to our information about the behaviour of the function f. The simplest example of

the usefulness of higher derivatives is the sign of the second derivative. If f

(x) is

positive on an interval [a, b], then the derivative f

(x) is increasing over this range.

Thus the graph of f is seen to curve upward [even if f

(x) < 0] and f is said

to be convex or concave up. See Exercise 6.2.J. Likewise, if f

(x) is negative

over an interval, then the derivative of f is decreasing and the graph of f curves

downward. Functions with such graphs are called concave or concave down. For

this reason, the points at which f

(x) changes sign are called inﬂection points to

indicate that the curvature of the graph changes direction. These points are easily

identiﬁed by eye; see Figure 6.5. Similar changes in higher derivatives are not so

easily recognized, as they have a more subtle effect.

Notice that the ideas of convex and concave also make sense for functions

that are not differentiable. We study such nondifferentiable convex functions in

Chapter 16.

y = f(x)

FIGURE 6.5. An inﬂection point: f

changes sign at c.

Exercises for Section 6.2

A. If f and g are differentiable on [a, b] and f

(x) = g

(x) for all a < x < b, show that

g(x) = f(x) + C for some constant C.

B. If f is strictly increasing on [a, b], is f

(x) > 0 for all x ∈ (a, b)?

C. Suppose that f is C

on (a, b), and f has four zeros in (a, b). Show that f

(3)

has a

zero.

152 Differentiation and Integration

D. (a) Show that tanx > x +

for 0 < x <

(b) Show that tanx < x +

for 0 < x < 1.

E. Suppose that f is continuous on an interval [a, b] and is differentiable at all points of

(a, b) except possibly at a single point x

∈ (a, b). If lim

x→x

(x) exists, show that

) exists and f

) = lim

x→x

(x).

HINT: Consider the intervals [x

, x

+ h] and [x

− h, x

F. (a) Show that the error between a differentiable function f(x) on [a, b] and the tan-

gent line T (x) to f at a may be estimated by |f (x) − T (x)| ≤ C|x − a|, where

C = sup

a≤y≤x

(y) − f

(a)|.

(b) Hence if f is C

, reﬁne this error estimate to |f(x) − T (x)| ≤ D|x − a|

, where

D = sup

a≤y≤x

(y)|.

G. (a) Let f(x) = x

sin(1/x) for x 6= 0 and f(0) = 0 as in Example 6.1.7. Show that

0 is a critical point of f that is not a local maximum nor a local minimum nor an

inﬂection point.

(b) Let g(x) = 2x

+ f(x). Show that g does have a global minimum at 0, but g

(x)

changes sign inﬁnitely often on both (0, ε) and (−ε, 0) for any ε > 0.

(0) > 0 but h is not monotone increasing on

any interval including 0.

H. (a) Suppose that g is C

on [a, b]. Prove that for every ² > 0, there is δ > 0 so that

g(d) − g(c)

d − c

< ε for all points c, d ∈ [a, b] with 0 < |d − c| < δ.

HINT: Use the Mean Value Theorem (MVT) and the fact that g

is uniformly con-

tinuous.

(b) Use this to give a second proof that the function f of Example 6.1.7 is not C

[0, 1].

I. Suppose that f is differentiable on [a, b] and f

(a) < 0 < f

(b).

(a) Show that there are points a < c < d < b such that f (c) < f (a) and f(d) < f(b).

(b) Show that the minimum on [a, b] occurs at an interior point.

in (a, b) such that f

) = 0.

(d) Prove Darboux’s Theorem: If f is differentiable on [a, b] and f

(a) < L < f

(b),

then there is a point x

in (a, b) at which f

) = L.

J. A function f is convex on an interval [a, b] if f(tx + (1−t)y) ≤ tf (x) + (1−t)f(y)

for all x, y ∈ [a, b] and all t ∈ [0, 1]. In other words, the graph of f is below the line

segment joining (x, f(x)) and and (y, f(y)) for all x, y ∈ [a, b].

(a) If f is differentiable on [a, b] and f

is increasing, then f is convex on [a, b].

HINT: If x < y and z = tx + (1 −t)y, apply the MVT to [x, z] and [z, y].

(b) If f is C

on an interval [a, b] and for some x

∈ [a, b], f

) > 0, then f is

convex in some interval about x

on an interval [a, b] and f

(x) ≥ 0 for all x ∈ (a, b), show that f is

convex on [a, b].

K. Suppose that f is differentiable on [0, ∞) and f

is strictly increasing.

(a) Show that f

(x) is continuous.