Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

6.3 Riemann Integration 163

D. Show that if f and g are Riemann integrable on [a, b], then so is αf + βg; and

αf(x) + βg(x) dx = α

f(x) dx + β

g(x) dx.

E. We call f : [a, b] → R a step function if there is a partition of [a, b] so that f is

constant on each interval of the partition. Show that every step function is Riemann

integrable using two arguments: ﬁrst, using Riemann’s condition (Theorem 6.3.5) and

second, using Condition (3) from Theorem 6.3.8.

F. Show that every piecewise continuous function is Riemann integrable. (This subsumes

the previous exercise.)

G. Show that if f is Riemann integrable on [a, b], then so is |f|.

HINT: Show that M

(|f|, P ) − m

(|f|, P ) ≤ M

(f, P ) − m

(f, P ).

H. Showthat f is Riemann integrable if and only if for each ε > 0, thereare step functions

and f

on [a, b] with f

(x) ≤ f(x) ≤ f

(x) such that

(x) − f

(x) dx < ε.

I. (a) Show that if f ≥ 0 is Riemann integrable on [a, b], then

f(x) dx ≥ 0.

(b) Hence show that if f and g are Riemann integrable on [a, b] and f(x) ≤ g(x) for

a ≤ x ≤ b, then

f(x) dx ≤

g(x) dx.

f(x) dx

≤

|f(x)|dx.

J. Show that if f is Riemann integrable on [a, b] and c ∈ R, then the function g deﬁned

on [a + c, b + c] by g(x) = f(x − c) is also Riemann integrable and

b+c

a+c

g(x) dx =

f(x) dx.

This property is called translation invariance.

K. Suppose that f is Lipschitz with constant L on [a, b]. Prove that

f(x) dx −

j=1

≤

L. If f is Riemann integrable on [a, b], show that F (x) = c +

f(t) dt is Lipschitz.

M. Show that if f is integrable on [a, b], then it is integrable on each interval [c, d] ⊂ [a, b]

as well. Moreover, for a < c < b,

f(x) dx =

f(x) dx +

f(x) dx.

N. If b < a, deﬁne

f(x) dx = −

f(x) dx. Show that the formula of the previ-

ous exercise also holds for c outside [a, b]. On what interval should f be Riemann

integrable for the formula to make sense in this context?

164 Differentiation and Integration

O. Show that sin(csc(1/x)) is integrable. HINT: See the discussion of Example 6.3.12.

P. Verify the implication (4) implies (3) of Theorem 6.3.8 when the inﬁmum and supre-

mum over the intervals [x

j−1

, x

] are not attained.

Q. If f and g are both Riemann integrable on [a, b], show that fg is also integrable.

HINT: Use the identity f(x)g(x)−f(t)g(t) = f(x)

g(x)−g(t)

f(x)−f(t)

g(t)

to show that M

(fg, P ) − m

(fg, P ) is bounded by

kfk

∞

(g, P ) − m

(g, P )

+ kgk

∞

(f, P ) − m

(f, P )

R. Show that the function of Example 5.2.10 is Riemann integrable, even though it is

discontinuous at every rational number.

HINT: For ε > 0, there are only ﬁnitely many points taking values greater than ε.

Choose a partition that includes those points in very small intervals.

S. Improper Integrals. Say that f is Riemann integrable on [a, ∞) if lim

b→∞

f(x) dx

exists. Use

∞

f(x) dx to denote this limit.

(a) For which real values of p does

∞

(logx)

dx exist?

(b) Show that

∞

sinx

dx exists.

HINT: Consider the alternating series

n≥0

(n+1)π

nπ

sinx

dx.

T. If f is unbounded as it approaches a, we deﬁne an improper integral by

lim

ε→0

a+ε

f(x) dx, when the limit exists. Of course,

f(x) dx is used to denote this

limit, so you have to keep an eye out for unbounded functions.

(a) For which real values of p does

dx exist?

(b) Show by example that lim

ε→0

a−ε

−b

f(x) dx +

a+ε

f(x) dx can exist even though

lim

ε→0

a+ε

f(x) dx does not.

6.4. The Fundamental Theorem of Calculus

The calculation of integrals via Riemann sums is of theoretical importance, but

it is not a simple method for evaluating integrals. Fortunately, there is a crucial

connection between integrals and derivatives that makes evaluating integrals by

hand practical and efﬁcient. We stress that this is not the deﬁnition of integral. The

word fundamental is used to emphasize that this is the central result connecting

differential and integral calculus. Nevertheless, it is not difﬁcult to prove.

6.4 The Fundamental Theorem of Calculus 165

6.4.1. FUNDAMENTAL THEOREM OF CALCULUS.

Let f be a bounded Riemann integrable function on [a, b], and let

F (x) =

f(t) dt for a ≤ x ≤ b.

Then F is a continuous function. If f is continuous at a point x

, then F is differ-

entiable at x

and F

) = f (x

Before proving this, we record the most useful consequence. A function f on

[a, b] has an antiderivative if there is a continuous function F(x) on [a, b] such that

(x) = f(x) for every point x ∈ (a, b). The second part of following theorem is

in fact valid for the larger class of functions that are Riemann integrable and have

antiderivatives, even though they are not continuous. This more technical result is

left to Exercise 6.4.J.

6.4.2. COROLLARY. Let f be a continuous function on [a, b]. Then f has an

antiderivative. Moreover, if G is any antiderivative of f, then

f(x) dx = G(b) − G(a).

PROOF. The Fundamental Theorem of Calculus shows that F (x) =

f(t)dt

is a differentiable function with F

= f. If G is any antiderivative of f , then

(G−F )

(x) = 0 for all x ∈ (a, b). By Corollary 6.2.5 of the Mean Value Theorem,

this means that G − F is some constant c, whence G = F + c. Finally,

G(b) − G(a) = F (b) − F (a) =

f(x) dx.

We require a simple estimate.

6.4.3. LEMMA. Suppose that f is an integrable function on [a, b] bounded by

M. Then

f(t) dt

≤ M (b − a).

PROOF. It is evident that for any partition P and any 1 ≤ j ≤ n,

−M ≤ m

(f, P ) ≤ M

(f, P ) ≤ M.

Hence U(f, P ) ≤

j=1

M(x

− x

j−1

) = M (b − a). Therefore,

f(t) dt = inf

U(f, P ) ≤ M(b − a).

Similarly, we obtain

f(t) dt = sup

L(f, P ) ≥ −M (b − a). ¥

166 Differentiation and Integration

PROOF OF THE FUNDAMENTAL THEOREM. Let f be bounded by M . For x, y

in [a, b], use the lemma to compute

|F (x) − F (y)| =

f(t) dt −

f(t) dt

≤ M |x − y|.

Hence F is Lipshitz with constant M and thus is continuous.

Now suppose that f is continuous at x

. Given ε > 0, choose δ > 0 so that

|y − x

| < δ implies that |f(y) − f(x

)| < ε. Then for |h| < δ, compute

F (x

+ h) − F (x

)

− f(x

)

f(t) dt −

f(x

) dt

f(t) − f(x

) dt

≤ ε.

The lemma was used again for the ﬁnal inequality. Thus

) = lim

h→0

F (x

+ h) − F (x

)

= f (x

So F has the desired derivative. ¥

6.4.4. REMARK. A jump discontinuity in the integrand f can result in a point

where the integral is not differentiable. For example, take f(x) = 1 for 0 ≤ x ≤ 1

and 2 for 1 < x ≤ 2. Then

F (x) =

f(t) dt =

(

x for 0 ≤ x ≤ 1

2x − 1 for 1 ≤ x ≤ 2.

This function is not differentiable at x = 1, but it does have a left derivative of 1

and a right derivative 2.

Nor is it the case that every differentiable function is an integral. An easy way

for this to fail is when the derivative is unbounded. Recall from Example 6.1.7,

the function F (x) = x

sin(1/x) on [0, 1] for some constant a in (1, 2). Then

(x) = ax

a−1

sin(1/x) − x

a−2

cos(1/x) for x > 0 and F

(0) = 0. Thus F is

differentiable, but the derivative is an unbounded function and thus is not Riemann

integrable.

We can take various formulae for differentiation and, using the Fundamental

Theorem, integrate them to obtain useful integration techniques. We are not con-

cerned here with the all tricks of the trade, but just a glance at the major methods.

Integration rules are more subtle than differentiation because it can be difﬁcult to

recognize which method to apply.

The product rule translates into integration by parts. We will assume that F

and G are C

to avoid pathology. Since (F G)

(x) = F

(x)G(x) + F (x)G

(x), we

obtain

(x)G(x) + F (x)G

(x) dx = F G

= F (b)G(b) − F (a)G(a).

6.4 The Fundamental Theorem of Calculus 167

Rearranging, we obtain the usual formulation

(x)G(x) dx = F G

−

F (x)G

(x) dx.

The chain rule corresponds to the substitution rule, also known as the change

of variable formula. Let u be a C

function on [a, b], and let F be C

on an

interval [c, d] containing the range of u. Then if G(x) = F (u(x)), the chain rule

states that G

(x) = F

(u(x))u

(x). Thus if we set f = F

f(u(x))u

(x) dx = G(b) − G(a)(6.4.5)

= F (u(b)) − F (u(a)) =

u(b)

u(a)

f(t) dt.

We interpret this as making the substitution t = u(x) and think of dt as u

(x) dx.

This change of variables is sometimes formulated somewhat differently. Sup-

pose that the function u satisﬁes u

(x) 6= 0 for all x ∈ [a, b]. If we set c = u(a)

and d = u(b), we obtain

f(x) dx =

−1

(d)

−1

(c)

f(u(t))u

(t) dt.(6.4.6)

This corresponds to the substitution x = u(t).

Without any attempt to be complete, we give a couple of examples of integra-

tion technique to refresh the reader’s memory. Introductory calculus textbooks are

full of further examples.

6.4.7. EXAMPLE. Consider

tan

−1

(x) dx. You will likely recall that the

derivative of tan

−1

(x) is

1 + x

, but the integral is probably not stored in memory.

This suggests that an integration by parts approach might help. Of course, you need

something to integrate, and so we put in a factor of 1, which integrates to x. Thus

tan

−1

(x) dx = x tan

−1

(x) −

1 + x

dx.

Now substitute u = 1 + x

, which has derivative du = 2x dx, to obtain

= x tan

−1

(x) −

= x tan

−1

(x) −

logu

= x tan

−1

(x) −

log(1 + x

Thus

tan

−1

(x) dx = x tan

−1

(x) −

log(1 + x

)

−

log2.

168 Differentiation and Integration

6.4.8. EXAMPLE. Now consider the integral

√

dx. This integrand has a

complicated exponent,

√

x, which can be simpliﬁed by substituting x = u

. Then

dx = 3u

du and u =

√

x runs from 0 to 2. So we obtain

√

dx =

du.

This now can be integrated by parts twice by integrating e

and differentiating 3u

= 3u

−

6ue

= (3u

− 6u)e

= (3u

− 6u + 6)e

= 6(e

− 1)

Exercises for Section 6.4

A. Evaluate the following:

(a) lim

n→∞

j=1

n + jc

for c > 1

(b) lim

n→∞

a+1

+ ··· +

(n − 1)

a+1

for a > −1.

HINT: Recognize these as Riemann sums.

B. Deﬁne log(x), for x > 0, to be

dt. By manipulating integrals, show that

log(ab) = log(a) + log(b).

C. (a) Prove the Mean Value Theorem for Integrals: If f is a continuous function on

[a, b], then there is a point c ∈ (a, b) such that

b − a

f(x) dx = f(c).

(b) Show by example that this may fail for a Riemann integrable function that is not

continuous.

D. Let f(x) = sign(x), and F (x) = |x|. Show that f is Riemann integrable on [a, b] and

that

f(x) dx = F (b) − F (a) for any a < b. Why is F not an antiderivative of f?

E. Let f be a continuous function on R, and suppose that b(x) is a C

function. Deﬁne

G(x) =

b(x)

f(t) dt. Compute G

(x).

HINT: Let F (x) =

f(t) dt and note that G(x) = F (b(x)).

6.5 Wallis’s Product and Stirling’s Formula 169

F. Compute the following integrals:

(a)

logx

dx (b)

π/2

sin

√

cosx

dx (c)

125

√

t +

√

G. Let f be a continuous function on R, and ﬁx ε > 0. Deﬁne a function G by

G(x) =

x+ε

f(t) dt.

Show that G is C

and compute G

H. Let u be a strictly increasing C

function on [a, b].

(a) By considering the area under the graph plus the area between the graph and the

y-axis, establish the formula

u(x) dx +

u(b)

u(a)

−1

(t) dt = bu(b) − au(a).

(b) Use the substitution formula (6.4.5) using f(x) = u

−1

(x) and integrate the second

expression by parts to derive the same formula as in part (a).

I. (a) Let x(t) and y(t) be C

functions on [0, 1] such that x

(t) ≥ 0. Prove that the area

under the curve C = {(x(t), y(t)) : 0 ≤ t ≤ 1} is

y(t)x

(t) dt.

(b) Now suppose that C is a closed curve [i.e., (x(0), y(0)) = (x(1), y(1))] that

doesn’t intersect itself and that x

(t) changes sign only a ﬁnite number of times.

Prove that the area enclosed by C is

y(t)x

(t) dt

J. Suppose that a function f is Riemann integrable and has an antiderivative F . Prove

that

f(x) dx = F (b) − F (a).

HINT: Apply the Mean Value Theorem to obtain F (x

)−F (x

i−1

) = f(c

)(x

−x

i−1

)

for some c

∈ (x

i−1

, x

). Then apply Theorem 6.3.8 (4).

K. Suppose that f is twice differentiable on R and kfk

∞

= A and kf

∞

= C. Prove

that kf

∞

≤

√

2AC.

HINT: If f

) = b > 0, show that f

+ t) ≥ b − C|t|. Integrate from x

− b/C

to x

+ b/C.

6.5. Wallis’s Product and Stirling’s Formula

In this section, we will obtain Stirling’s formula, an elegant asymptotic formula

for n!, using only basic calculus. However, to get a sharp result, the estimates must

be done quite carefully. By a sharp inequality, we mean an inequality that cannot

be improved. For example, |sin(x)/x| ≤ 1 for x > 0 is sharp but tan

−1

(x) < 2 is

not. These estimates lead us to a general method of numerical integration. The ﬁrst

step is an exercise in integration that leads to a useful formula for π.

170 Differentiation and Integration

6.5.1. EXAMPLE. To begin, we wish to compute I

sin

x dx. We use

integration by parts and induction. If n ≥ 2,

sin

x dx =

sin

n−1

x sinx dx

= −sin

n−1

x cosx

(n − 1) sin

n−2

x cos

x dx

= (n − 1)

sin

n−2

x(1 − sin

x) dx = (n − 1)(I

n−2

− I

Solving for I

, we obtain a recursion formula

n − 1

n−2

Rather than repeatedly integrating by parts, we use this formula. For example,

5π

Since the formula drops the index by 2 each time, we end up at a multiple of I

= π

if n is even and a multiple of I

= 2 when n is odd. Indeed,

···

2n − 3

2n − 2

2n − 1

2n+1

···

2n − 2

2n − 1

2n + 1

Since 0 ≤ sinx ≤ 1 for x ∈ [0, π], we have sin

2n+2

x ≤ sin

2n+1

x ≤ sin

Therefore, I

2n+2

≤ I

2n+1

≤ I

. Divide through by I

and use the preceding

formula to obtain

2n + 1

2n + 2

≤

· 4

· 6

···(2n−2)

· (2n)

1 · 3

· 5

···(2n−1)

· (2n+1)

≤ 1.

Rearranging this slightly and taking the limit, we obtain Wallis’s product

= lim

n→∞

· 4

· 6

···(2n−2)

· (2n)

1 · 3

· 5

···(2n−1)

· (2n+1)

We estimate n! by approximating the integral of logx using the trapezoidal

rule, a modiﬁcation of Riemann sums. First verify that

logx dx = x log x − x

by differentiating. Notice that the second derivative of log x is −x

−2

, which is

negative for all x > 0. So the graph of logx is curving downward (i.e., this function

is convex). Rather than using the rectangular approximants used in Riemann sums,

we can do signiﬁcantly better by using a trapezoid. In other words, we approximate

the curve log x for x between k − 1 and k by the straight line segment connecting

(k −1, log(k −1)) to (k, logk). By the convexity, this line lies strictly below logx

and thus has a smaller area.

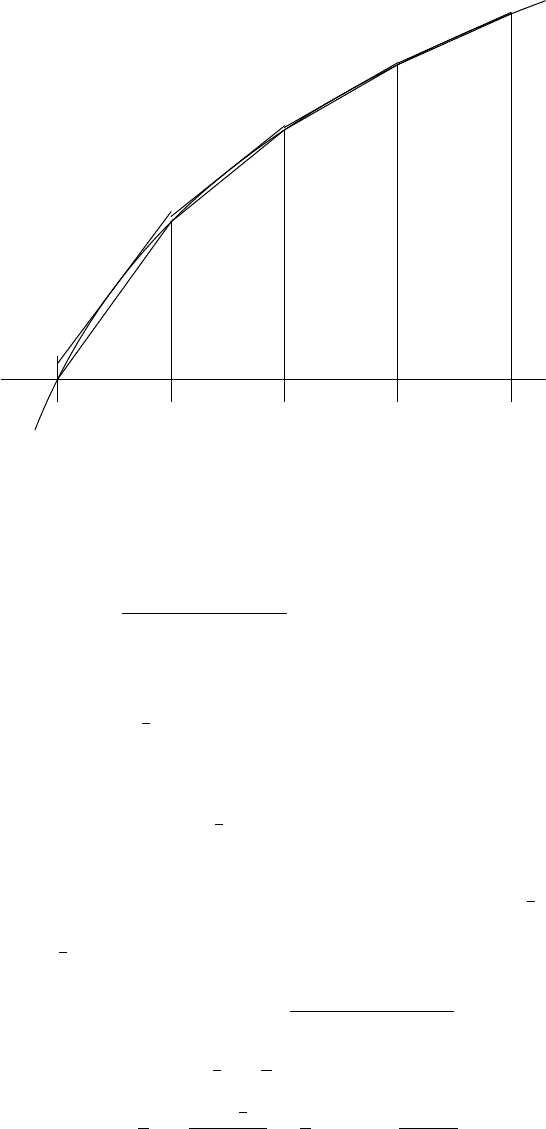
6.5 Wallis’s Product and Stirling’s Formula 171

1 2 3 4 5

FIGURE 6.9. The graph of log x with the tangent approximation

above and the trapezoidal approximation below.

The area of a trapezoid is the base times the average height. Therefore

log(k − 1) + logk

k−1

logx dx.

Sum this from 2 to n to obtain

n−1

k=2

logk +

logn <

logx dx = n log n − (n − 1).

This may be rearranged to compute the error as

:= (n +

) logn − (n − 1) − logn!.

To bound this error, let us estimate

k−1

logx dx from above by another trape-

zoid, as shown in Figure 6.9. The tangent line to logx at x = k −

lies strictly

above the curve because logx is concave. This yields a trapezoid with average

height log(k −

). Therefore,

k−1

logx dx −

log(k − 1) + logk

< log(k −

) −

log(k − 1)k

log

(k −

)

− k

log

1 +

4(k

−k)

172 Differentiation and Integration

Now for h > 0, log(1+h) =

1+h

dx <

1+h

1dx = h. Using this to simplify

our formula for ε

, we obtain ε

8(k

− k)

k − 1

−

Observe that this produces a telescoping sum

k=2

k − 1

−

1 −

Consequently, E

is a monotone increasing sequence that is bounded above by 1/8.

Therefore, lim

n→∞

= E exists.

To put this in the desired form, note that logn! + n −(n +

) logn = 1 −E

Exponentiating, we obtain

lim

n→∞

√

−n

= e

1−E

Rearranging and using only the estimate 0 ≤ E ≤ 1/8, we have the useful estimate

known as Stirling’s inequality:

√

n < n! < e

√

We will evaluate e

1−E

exactly. To this end, set a

√

−n

. Then

(n!)

2n+1

−2n

(2n)

√

2ne

−2n

(2n)!

n!)

(2n)!

· 4

· 6

···(2n − 4)

· (2n − 2)

· (2n)

1 · 2 ·3 ·4···(2n − 2) · (2n − 1) · (2n)

2 · 4 ·6···(2n − 4) · (2n − 2) · (2n)

1 · 3 ·5···(2n − 3) · (2n − 1)

2(2n + 1)

· 4

· 6

···(2n − 4)

· (2n − 2)

· (2n)

· 5

· 7

···(2n − 3)

· (2n − 1)

· (2n + 1)

Now combining this with our knowledge of Wallis’s product,

1−E

= lim

n→∞

= 2

√

2π.

So we obtain the following:

6.5.2. STIRLING’S FORMULA.

lim

n→∞

−n

√

2πn

= 1