Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

6.5 Wallis’s Product and Stirling’s Formula 173

Finally, let us look more closely at the trapezoidal approximation as a method

for computing integrals. Consider a continuous function f(x) on [a, b] and a uni-

form partition x

= a +

k(b−a)

for 0 ≤ k ≤ n. As previously, we estimate the

area

k−1

f(x) dx by the trapezoid with vertices (x

k−1

, f(x

k−1

)) and (x

, f(x

)).

This has base

b − a

and average height

f(x

k−1

) + f(x

)

. The approximation is

therefore

k=1

b − a

´³

f(x

k−1

) + f(x

)

b − a

f(x

) + f(x

) + ··· + f(x

n−1

) +

f(x

)

The crucial questions about this, or any approximation, are, ﬁrst, How close is

it to the true answer, and second, How much easier is it to work with? Ideally, an

approximation is both very close to the true answer and much easier to work with.

In practice, there is usually a trade-off between these two properties. We return

to this issue in detail when we consider approximating functions by polynomials

(Chapter 10) and by Fourier series (Chapter 14).

For the trapezoidal rule, so long as the function is C

, we can use the Mean

Value Theorem twice (once disguised as Rolle’s Theorem) to obtain an estimate

for the error.

6.5.3. TRAPEZOIDAL RULE.

Suppose f is a C

function on [a, b] and let kf

∞

= sup{|f

(x)| : x ∈ [a, b]}.

Then the trapezoidal approximants A

satisfy

f(x) dx − A

≤

(b − a)

∞

12n

PROOF. Let F (x) =

f(t) dt. For the interval [x

k−1

, x

], set

= F (x

) − F (x

k−1

) −

b − a

f(x

) − f(x

k−1

)

Deﬁne c =

k−1

+ x

) and consider the function

G(t) = F (c + t) − F (c − t) − t

f(c + t) + f (c − t)

− Bt

Notice that G(0) = 0. We are of course interested in t

= (b − a)/2n. So we

choose the constant B so that G(t

) = 0, namely B = ε

By Rolle’s Theorem, there is a point t

∈ (0, t

) so that G

) = 0. By the

Fundamental Theorem of Calculus and the chain rule,

F (c + t) − F (c − t)

= f (c + t) + f(c − t).

Therefore,

(t) = t

(c + t) − f

(c − t)

− 3Bt

174 Differentiation and Integration

Substituting t

and solving for B yields

B =

(c + t

) − f

(c − t

)

An application of the Mean Value Theorem produces a point t

∈ (0, t

) so that

(c + t

) − f

(c − t

)

= f

)

and hence B = 2f

)/3. Consequently,

|ε

| = |Bt

| =

(b − a)

)

12n

≤

(b − a)

∞

12n

Summing from 1 to n yields

f(x) dx − A

≤

k=1

|ε

| ≤

(b − a)

∞

12n

. ¥

Exercises for Section 6.5

A. Evaluate lim

n→∞

√

B. Estimate the choice of n to guarantee an approximation to

dx to 4 decimals

accuracy using the trapezoidal rule.

C. For every Riemann integrable function, f, use the trapezoidal rule to obtain a sequence

converging to

f(x) dx.

D. Simpson’s Rule. This method for estimating integrals is based on approximating the

function by a parabola passing through three points on the graph of f . Given a uniform

partition P = {a = x

< . . . < x

= b}, let y

= f(x

) for all k.

(a) Find the parabola passing through (x

2k−2

, y

2k−2

), (x

2k−1

, y

2k−1

) and (x

, y

(b) Find the integral of this parabola from x

2k−2

to x

f(x) dx:

b − a

+ 4y

+ 2y

+ 4y

+ ··· + 2y

2n−2

+ 4y

2n−1

+ y

E. Decide whether

n≥0

2n+k

√

2n + k

converges.

F. The gamma function is deﬁned by Γ(x) =

∞

x−1

−t

dt for all x > 0.

(a) Prove that this improper integral has a ﬁnite value for all x > 0.

(b) Prove that Γ(x + 1) = xΓ(x). HINT: Integrate by parts.

(d) Calculate Γ(

). HINT: Substitute t = u

, write the square as a double integral,

and convert to polar coordinates.

6.6 Measure Zero and Lebesgue’s Theorem 175

6.6. Measure Zero and Lebesgue’s Theorem

As we have already said, it is possible to build a more powerful theory of

integration, based on the ideas of measure theory. The ﬁrst step toward this theory,

and the crucial notion for this section, is the idea of a set of measure zero. This

is a reasonable condition for a set to be “small,” although the condition can have

surprising and unintuitive properties. Using this idea, we obtain a characterization

of precisely which functions are Riemann integrable.

If U = (c, d) is an open interval, let us write |U| = d − c for its length.

6.6.1. DEFINITION. A subset A of R has measurezeroif for every ε > 0, there

is a countable family of intervals {U

= (c

, d

) : n ≥ 1} such that A ⊂

n≥1

and

n≥1

| =

n≥1

− c

< ε.

A subset A of (a, b) has content zero if for every ε > 0, there is a ﬁnite

family of intervals {U

= (c

, d

) : 1 ≤ n ≤ N } such that A ⊂

n=1

and

n=1

| < ε.

6.6.2. EXAMPLES.

(1) The set Q of all rational numbers has measure zero. To see this, write Q as a

list r

, r

, . . . . Given ε > 0, let U

= (r

− 2

−n−1

ε, r

+ 2

−n−1

ε). Evidently,

n≥1

contains Q and

n≥1

| =

n≥1

−n

ε = ε. So Q has measure zero.

However, Q does not havecontent zero because any ﬁnite collection of intervals

covering Q can miss only ﬁnitely many points in R. Consequently, at least one

would be inﬁnite! In fact, the set of rational points in [0, 1] will not have content

zero either for the same reason combined with the next example.

(2) Suppose that an interval [a, b] is covered by open intervals {U

}. Now [a, b] is

compact by the Heine–Borel Theorem (Theorem 4.4.6). Moreover by the Borel–

Lebesgue Theorem (Theorem 9.2.3), the open cover {U

} has a ﬁnite subcover,

say U

, . . . , U

. Now this ﬁnite set of intervals pieces together to cover an interval

of length b − a. From this we can easily show that

n=1

− c

≥ b − a.

Consequently, [a, b] does not have measure zero. (It has measure b − a.)

(3) In Example 4.4.8, we constructed the Cantor set. We showed there that it has

measure zero and indeed has content zero. It also shows that an uncountable set

can have measure zero.

6.6.3. PROPOSITION.

(1) If A has measure zero, and B ⊂ A, then B has measure zero.

(2) If A

are sets of measure zero for n ≥ 1, then

n≥1

has measure zero.

(3) Every countable set has measure zero.

(4) If A is compact and has measure zero, then it has content zero.

176 Differentiation and Integration

PROOF. (1) is trivial. For (2), suppose that ε > 0. We modify the argument in

Example 6.6.2 (1). Choose a collection of open intervals {U

: m ≥ 1} covering

such that

m≥1

| < 2

−n

ε. Then {U

: m, n ≥ 1} covers

n≥1

and

the combined lengths of these intervals is

n≥1

m≥1

| <

n≥1

−n

ε = ε.

(3) now follows from (2) and the observation that a single point has measure zero.

(4) Suppose that A is compact and {U

} is an open cover of intervals with

n≥1

| < ε. By the Borel–Lebesgue Theorem, this cover has a ﬁnite subcover.

This ﬁnite cover has total length less than ε also. Therefore, A has content zero. ¥

6.6.4. DEFINITION. A property is valid almost everywhere (a.e.) if the set of

points where it fails has measure zero.

For example, f = g a.e. means that {x : f (x) 6= g(x)} has measure zero. And

f(x) = lim

n→∞

(x) a.e. means that this limit exists and equals f(x) except on a set

of measure zero.

It is important to distinguish between two similar but distinct statements. If f is

continuous almost everywhere, then the set of points of discontinuity has measure

zero. If f equals a continuous function almost everywhere, then there would be

a continuous function g so that {x : f (x) 6= g(x)} is measure zero. This is a

much stronger property. For example, the characteristic function of [0, 1] has only

two points of discontinuity in R and thus is continuous almost everywhere. But any

continuous function will differ from this on a whole interval near 0 and another near

1. Since these intervals are not measure zero (see Example 6.6.2), the continuous

function is not equal to the characteristic function almost everywhere.

The next result is very appealing because it provides a simple description of

exactly which functions are integrable. But in practice, it is often enough to know

that piecewise continuous functions are integrable. It will be more useful to build a

more powerful integral, as we do in Section 9.6.

We need a notion of the “size” of a discontinuity. There is a global version of

this concept, known as the modulus of continuity, which we will develop later (see

Deﬁnition 10.4.2).

6.6.5. DEFINITION. The oscillation of a function f over an interval I is deﬁned

as osc(f, I) = sup{|f(x) − f(y)| : x, y ∈ I}. Then set

osc(f, x) = inf

r>0

osc

f, (x − r, x + r)

It is easy (Exercise 6.6.A) to prove that f is continuous at x if and only if

osc(f, x) = 0.

6.6.6. LEBESGUE’S THEOREM.

A bounded function on [a, b] is Riemann integrable if and only if it is continuous

almost everywhere.

6.6 Measure Zero and Lebesgue’s Theorem 177

PROOF. First suppose that f is Riemann integrable. Then for each k ≥ 1, there is

a ﬁnite partition P

of [a, b] so that U (f, P

), −L(f, P

) < 4

−k

. Let u

and l

the step functions that are constant on the intervals of P

and bound f from above

and below (as in Exercise 6.3.H) so that

(x) − l

(x) dx < 4

−k

The set B

= {x : u

(x) − l

(x) ≥ 2

−k

} is the union of certain intervals of

the partition P

, say J

k,i

for i ∈ S

. Compute

−k

(x) − l

(x) dx ≥

i∈S

−k

k,i

Then

i∈S

k,i

| < 2

−k

. Let A

k≥1

intB

and let A

k≥1

. Observe

that {intJ

k,i

: i ∈ S

} covers A

for each k. As these intervals have length sum-

ming to less than 2

−k

, it follows that A

has measure zero. Since A

is countable,

it also has measure zero. Thus the set A = A

∪ A

has measure zero.

For any x 6∈ A and any ε > 0, choose k so that 2

−k

< ε and x 6∈ B

. Then

(x) − l

(x) < 2

−k

< ε. As x is not a point in P

, it is an interior point of some

interval J of this partition. Choose r > 0 so that (x − r, x + r) ⊂ J. For any y

with |x − y| < r, we have l

(x) ≤ f(y), f(x) ≤ u

(x). Thus |f(x) − f(y)| < ε

and so f is continuous at x.

Conversely, suppose that f is continuous almost everywhere on [a, b] and is

bounded by M. Let

= {x ∈ [a, b] : osc(f, x) ≥ 2

−k

Then each A

has measure zero, and the set of points of discontinuity is A =

k≥1

. Observe that A

is closed. Indeed suppose that x is the limit of a se-

quence (x

) with all x

in A

. By deﬁnition, there are points y

and z

with

− y

| < 1/n and |x

− z

| < 1/n such that |f(y

) − f (z

)| ≥ 2

−k

− 2

−n

Therefore,

lim

n→∞

= lim

n→∞

= x.

Consequently, osc(f, x) ≥ 2

−k

By Proposition 6.6.3(4), each A

has content zero. Cover A

with a ﬁnite

number of open intervals J

k,i

such that

k,i

| < 2

−k

. The complement X

consists of a ﬁnite number of closed intervals on which osc(f, x) < 2

−k

for all

x ∈ X. Thus there is an open interval J

containing x so that osc(f, J

) < 2

−k

Notice that X is a closed and bounded subset of [a, b] and so is compact. The

collection {J

: x ∈ X} is an open cover of X. By the Borel–Lebesgue Theorem,

there is a ﬁnite subcover J

, . . . , J

. Let P

be the ﬁnite partition consisting of

all the endpoints of all of these intervals together with the endpoints of each J

k,i

Let us estimate the upper and lower sums for this partition. As usual, let

(f, P

) and m

(f, P

) be the supremum and inﬁmum of f over the jth interval,

namely I

k,j

= [x

k,j−1

, x

k,j

]. These intervals split into two groups, those contained

in X and those contained in U

k,i

. For the ﬁrst group, the oscillation is less

than 2

−k

and thus M

− m

≤ 2

−k

. For the second group, the total length of the

178 Differentiation and Integration

intervals is at most 2

−k

. Combining these estimates, we obtain

U(f, P

) − L(f, P

) =

k,i

⊂X

− m

)∆

k,i

⊂U

− m

)∆

≤

k,i

⊂X

−k

∆

k,i

⊂U

2M∆

≤ 2

−k

(b − a) + 2M2

−k

= 2

−k

(b − a + 2M).

Therefore, lim

k→∞

U(f, P

) − L(f, P

) = 0, and so f is integrable by Riemann’s

condition. ¥

You may want to review the examples of discontinuous functions in Section 5.2

to see which are equal to a continuous function almost everywhere.

Exercises for Section 6.6

A. Prove that f is continuous at x if and only if osc(f, x) = 0.

B. If measure zero sets were deﬁned using closed intervals instead of open intervals, show

that one obtains the same sets.

C. If A ⊂ R has measure zero, what is int(A)? Is

A also measure zero?

D. If A has measure zero and B is countable, show that A + B = {a + b : a ∈ A, b ∈ B}

has measure zero.

E. Consider the set C

obtained using the construction of the Cantor set in Example 4.4.8

but removing 2

n−1

intervals of length 4

−n

(instead of length 3

−n

) at the nth stage.

(a) Show that C

is closed and has no interior.

(b) Show that C

is not measure zero.

HINT: Any cover of C

together with the intervals removed covers [0, 1].

F. Let D be the set of numbers x ∈ [0, 1] with a decimal expansion containing no odd

digits. Prove that D has measure zero.

HINT: Cover D with some intervals of length 10

−n

G. Suppose that f and g are both Riemann integrable on [a, b]. Use Lebesgue’s Theorem

to prove that f g is Riemann integrable. (Compare with Exercise 6.3.Q.)

H. Show that A ⊂ R has content zero if and only if A is compact and has measure zero.

HINT: Show that an unbounded set cannot have content zero. Note that a ﬁnite open

cover of A contains most of A.

I. Deﬁne a relation on functions on [a, b] by f ∼ g if the set {x : f(x) 6= g(x)} has

measure zero. Prove that this is an equivalence relation.

CHAPTER 7

Normed Vector Spaces

In this chapter, we generalize to vector spaces the absolute value function on R

and the norm of a vector in R

. From this perspective, convergence of functions

is similar to convergence of points in R. The additional complication comes from

the fact that these vector spaces are generally inﬁnite dimensional. The notions

of topology go through with almost no change in the deﬁnitions. However, the

theorems can be quite different. For example, being closed and bounded is not

sufﬁcient to imply compactness in inﬁnite-dimensional spaces such as C[a, b]. In

particular, we develop the properties of inner product spaces in detail because these

spaces are especially useful and tractable.

7.1. Deﬁnition and Examples

Recall that a vector space over R is a set V together with two operations, vector

addition and scalar multiplication. Vector spaces are discussed in more detail in

Section 1.4; an important example of a vector space, R

, is the focus of Chapter 4.

We write x+y for vector addition and αx for scalar multiplication, where x, y ∈ V

and α ∈ R.

7.1.1. DEFINITION. Let V be a vector space over R. A norm on V is a function

k · k on V taking values in [0, +∞) with the following properties:

(1) (positive deﬁnite) kxk = 0 if and only if x = 0,

(2) (homogeneous) kαxk = |α|kxk for all x ∈ V and α ∈ R, and

(3) (triangle inequality) kx + yk ≤ kxk + kyk for all x, y ∈ V .

We call the pair (V, k · k) a normed vector space.

The ﬁrst two properties are usually easy to verify. The positivedeﬁnite property

just says that nonzero vectors have nonzero length. And the homogeneous property

says that the norm is scalable. The important property, which often requires some

cleverness to verify, is the triangle inequality. It says that the path from point A to

B and on to C is at least as long as the direct route from A to C. As we indicated

179

180 Normed Vector Spaces

in Figure 4.1 in Chapter 4, this algebraic inequality is equivalent to the geometric

statement that the length of one side of a triangle is at most sum of the lengths of

the other two sides.

7.1.2. EXAMPLE. Consider the vector space R

. In Chapter 4, we showed that

the Euclidean norm

kxk = k(x

, . . . , x

i=1

1/2

is a norm. Indeed, properties (1) and (2) are evident, and the triangle inequality was

a consequence of Schwarz’s inequality.

Consider two other functions:

kxk

= k(x

, . . . , x

i=1

kxk

∞

= k(x

, . . . , x

∞

= max

1≤i≤n

Again it is easy to see that they are positive deﬁnite and homogeneous. The key is

the triangle inequality. But for these functions, even that is straightforward. Com-

pute

kx + yk

i=1

+ y

≤

i=1

| + |y

| = kxk

+ kyk

and

kx + yk

∞

= max

1≤i≤n

+ y

≤ max

1≤i≤n

| + max

1≤i≤n

| = kxk

∞

+ kyk

∞

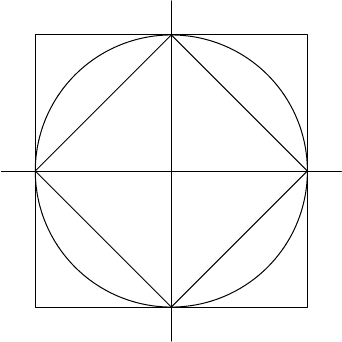
To illustrate the differences between these norms, consider the vectors of norm

at most 1 in R

for these three norms, as given in Figure 7.1. This set is sufﬁciently

useful that we give it a name. For any normed vector space (V, k · k), the unit ball

of V is the set {x ∈ V : kxk ≤ 1}.

The next example is very important for our applications as it allows us to apply

vector space methods to collections of functions; that is, to think of functions as

vectors.

7.1.3. EXAMPLE. Let K be a compact subset of R

, and let C(K) denote

the vector space of all continuous real-valued functions on K. If f, g ∈ C(K)

and α ∈ R, then f + g is the function given by (f + g)(x) := f(x) + g(x) and

(αf)(x) := αf(x). There are several different possible norms on C(K). The most

7.1 Deﬁnition and Examples 181

1−1

−1

FIGURE 7.1. The unit balls {(x, y) : k(x, y)k

≤ 1} for p = 1, 2, ∞.

natural and most important is the uniform norm, given by

kfk

∞

= sup

x∈K

|f(x)|.

By the Extreme Value Theorem (Theorem 5.4.4), |f|achieves its maximum at some

point x

∈ K. So using this point x

, we have kfk

∞

= |f (x

)| < ∞.

Clearly, thisfunction is nonnegative. To see that it is really a norm, observe ﬁrst

that if kfk

∞

= 0, then |f(x)| = 0 for all x ∈ K and so f = 0. For homogeneity,

we have

kαfk

∞

= sup

x∈K

|αf(x)| = |α| sup

x∈K

|f(x)| = |α|kfk

∞

Finally, the triangle inequality is proved as follows:

kf + gk

∞

= sup

x∈K

|f(x) + g(x)|

≤ sup

x∈K

|f(x)| + |g(x)|

≤ sup

x∈K

|f(x)| + sup

x∈K

|g(x)| = kfk

∞

+ kgk

∞

We shall see in Chapter 8 that a sequence of functions f

converges to a function f

C(K), k · k

∞

if and only if the sequence converges uniformly. Since uniform

convergence is often the “right” notion of convergence for many applications, we

will use this normed vector space often.

Controlling the derivatives of a function, as well as the function itself, is often

important. Fortunately, this is easy to do, and we will regularly use normed vector

spaces like the following example.

7.1.4. EXAMPLE. For simplicity, we restrict our attention to an interval of R,

but the same idea readily generalizes. Let C

[a, b] denote the vector space of all

functions f : [a, b] → R such that f and its ﬁrst 3 derivatives f

, f

000

are all

182 Normed Vector Spaces

deﬁned and continuous. Using f

(j)

for the jth derivative (and f

(0)

for f), we can

deﬁne a new norm k · k

kfk

= max

0≤j≤3

(j)

∞

where k · k

∞

is the uniform norm on the interval [a, b] introduced in the previous

example.

It is an exercise to verify that this is a norm. In order for a sequence of func-

tions f

in C

[a, b] to converge to a function f, the functions and their ﬁrst three

derivatives f

(j)

for 0 ≤ j ≤ 3 must all converge uniformly to the corresponding

derivative f

(j)

Clearly, this example can be generalized by considering the ﬁrst p derivatives,

for any positive integer p instead of just p = 3.

7.1.5. EXAMPLE. For certain applications, we’ll need the L

norms on C[a, b].

Fix a real number p in [1, ∞). The L

[a, b] norm is deﬁned on C[a, b] by

kfk

|f(x)|

1/p

First notice that kfk

≥ 0. Moreover, if f 6= 0, then there is a point x

∈ [a, b]

such that f(x

) 6= 0. Take ε = |f(x

)|/2 and use the continuity of f to ﬁnd an

r > 0 so that

|f(x) − f(x

)| <

|f(x

for x

− r < x < x

+ r.

Hence

|f(x)| ≥ |f(x

)| − |f(x) − f(x

)| >

|f(x

for x

−r < x < x

+r. We may suppose that r is small enough so that a ≤ x

−r

and x

+ r ≤ b. (If x

= a or b, the simple modiﬁcation is left to the reader.)

Consequently,

kfk

≥

−r

|f(x

1/p

≥

(2r)

1/p

|f(x

> 0.

So the p-norms are positive deﬁnite.

Homogeneity is easy to verify from the deﬁnition. However, the triangle in-

equality is tricky, unless p is 1 or 2. We leave the general case to Section 7.7,

where we study L

spaces in more detail. The case p = 2 is easier because it arises

from an inner product (much as the Euclidean norm on R

is obtained from the dot

product). We prove it in Section 7.3.