Davidson K.R., Donsig A.P. Real Analysis with Real Applications
Подождите немного. Документ загружается.


7.5 Orthogonal Expansions in Inner Product Spaces 203
Thus e is orthogonal to M. In particular, {e, e
i
: i ≥ 1} is orthonormal, which
contradicts the maximality of E. Since E is maximal, it follows that M = H.
Parseval’s Theorem shows that the closed span of an orthonormal set consists
of all `
2
combinations of this orthonormal set. So every vector x ∈ H may be
expressed as
∞
P
i=1
α
i
e
i
. The coefficients are unique because this expression for x
implies that
hx, e
j
i = lim
n→∞
n
X
i=1
α
i
e
i
, e
j
®
=
n
X
i=1
α
i
he
i
, e
j
i = α
j
¥
Exercises for Section 7.5
A. When does equality hold in Equation (7.5.3)?
B. Let x = (x
n
)
∞
n=1
and y = (y
n
)
∞
n=1
be elements of `
2
.
(a) Show that
N
P
n=1
|x
n
y
n
| ≤ kxkkyk. HINT: Schwarz inequality.
(b) Hence prove that
∞
P
n=1
x
n
y
n
converges absolutely.
C. If M is a closed subspace of a Hilbert space H, define the orthogonal complement
of M to be M
⊥
= {x : hx, mi = 0 for all m ∈ M}.
(a) Show that every vector in H can be written uniquely as x = m + y, where m ∈ M
and y ∈ M
⊥
. Moreover, kxk
2
= kmk
2
+ kyk
2
.
(b) Show that M = (M
⊥
)
⊥
.
D. Let P be a projection on an inner product space V . Prove that the following are
equivalent:
(a) P is an orthogonal projection.
(b) kvk
2
= kP vk
2
+ kv − P vk
2
for all v ∈ V .
(c) kP vk ≤ kvk for all v ∈ V .
(d) hP v, wi = hv, P wi for all v, w ∈ V .
HINT: For (c) =⇒ (d), show that not (d) implies there are vectors v = P v and
w = (I −P )w such that hv, wi > 0. Compute kv −twk
2
−kvk
2
for small t > 0. For
(d) =⇒ (a), show that hP v, (I − P )wi = 0.
E. Show that the orthogonal projection P onto a subspace M is unique.
HINT: If P and Q are orthogonal projections onto M , apply Q to x = P x+ (I −P )x.
F. Formulate and prove a precise version of the following statement “A separable infinite-
dimensional Hilbert space with an orthonormal basis {e
n
: n ≥ 1} behaves like `
2
.”
HINT: Look at the finite-dimensional statement, Corollary 7.4.8.
G. Let M and N be closed subspaces of a Hilbert space H.
(a) Show that (M ∩ N )
⊥
=
M
⊥
+ N
⊥
.
(b) Let {e
n
: n ≥ 1} be an orthonormal basis for `
2
. Let M = span{e
2n
: n ≥ 1} and
N = span{e
2n−1
+ ne
2n
: n ≥ 1}. Show that M + N is not closed.
(c) Use (b) to show that closure is needed in part (a).

204 Normed Vector Spaces
H. Consider the functions f
n
in C[−π, π] given by
f
n
(x) =
0 −π ≤ x ≤ 0
nx 0 ≤ x ≤
1
n
1
1
n
≤ x ≤ π.
(a) Show that f
n
converges in the L
2
norm to the characteristic function
χ
of (0, π]. In
particular, (f
n
)
∞
n=1
is an L
2
-Cauchy sequence.
(b) Show that k
χ
− hk
2
> 0 for every function h in C[−π, π].
(c) Hence conclude that C[−π, π] is not complete in the L
2
norm.
I. Let {r
n
: n ≥ 1} be a list of the rational points in [0, 1]. Define an inner product on
C[0, 1] by hf, gi
∗
=
∞
P
n=1
2
−n
f(r
n
)g(r
n
).
(a) Show that this is indeed a positive definite inner product.
(b) Why is this not an inner product on the vector space of all bounded functions on
[0, 1]?
(c) Show that C[0, 1] is not complete in this inner product norm.
HINT: Find a Cauchy sequence converging to the characteristic function of {0}.
7.6. Finite-Dimensional Normed Spaces
In this section, we will study the finite-dimensional subspaces of an arbitrary
normed vector space. Many of the nice properties of R
n
carry over to this setting.
A particularly important result is Theorem 7.6.5, which will be very useful in the
chapter on approximation.
7.6.1. LEMMA. If {v
1
, v
2
, . . . , v
n
} is a linearly independent set in a normed
vector space (V, k · k), then there exist positive constants 0 < c < C so that for all
a = (a
1
, . . . , a
n
) ∈ R
n
, we have
ckak
2
≤
°
°
°
n
X
i=1
a
i
v
i
°
°
°
≤ Ckak
2
PROOF. By the triangle inequality and the Schwarz inequality (4.1.1),
°
°
°
n
X
i=1
a
i
v
i
°
°
°
≤
n
X
i=1
|a
i
|kv
i
k
≤
³
n
X
i=1
a
2
i
´
1/2
³
n
X
i=1
kv
i
k
2
´
1/2
= Ckak
2
,
where C =
³
n
P
i=1
kv
i
k
2
´
1/2
.
7.6 Finite-Dimensional Normed Spaces 205
Define a function N on R
n
by N(a) =
°
°
°
n
P
i=1
a
i
v
i
°
°
°
. Observe that N is a con-
tinuous function since
|N(x) − N(y)| =
¯
¯
¯
¯
°
°
°
n
X
i=1
x
i
v
i
°
°
°
−
°
°
°
n
X
i=1
y
i
v
i
°
°
°
¯
¯
¯
¯
≤
°
°
°
n
X
i=1
(x
i
− y
i
)v
i
°
°
°
≤ Ckx − yk
2
.
So N is Lipschitz and thus continuous.
Let S = {a ∈ R
n
: kak
2
= 1} be the unit sphere of R
n
. Since the set
{v
1
, . . . , v
n
} is linearly independent, it follows that N(x) > 0 when x 6= 0. In
particular, N never vanishes on the compact set S. By the Extreme Value Theorem
(Theorem 5.4.4), N must achieve its minimum value c at some point on S; whence
c > 0. So if a is an arbitrary vector in R
n
, we obtain
°
°
°
n
X
i=1
a
i
v
i
°
°
°
= kak
2
N(a/kak
2
) ≥ ckak
2
.
¥
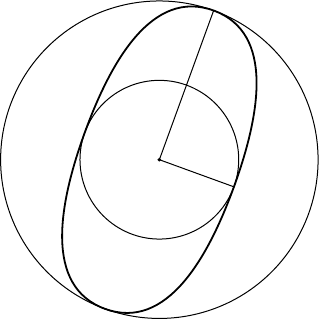
0
c
C
FIGURE 7.3. Euclidean balls inside and outside the unit ball of V .
The effect of this theorem is that every finite-dimensional normed space has
the same topology as (R
n
, k·k
2
), in the sense that they have the “same” convergent
sequences, the “same” open sets, and so on. Let us make this more precise. If
{v
1
, v
2
, . . . , v
n
} is a basis for an n-dimensional normed space V , define a linear
transformation from R
n
into V by T a =
n
P
i=1
a
i
v
i
. The map T carries R
n
one-to-
one and onto V by the definition of a basis. Since every element of V is a linear
combination of {v
1
, . . . , v
n
}, we can define the inverse map by T
−1
n
P
i=1
a
i
v
i
= a.

206 Normed Vector Spaces
7.6.2. COROLLARY. Suppose that V is an n-dimensional normed space with
basis {v
1
, v
2
, . . . , v
n
}. Then the maps T and T
−1
defined previously are both Lip-
schitz, and therefore continuous. Thus a set A in R
n
is closed, bounded, open, or
compact if and only if T (A) is closed, bounded, open, or compact in V .
PROOF. We have for vectors x and y in R
n
,
kT x − T yk = N(x − y) ≤ Ckx − yk
2
.
So T is Lipschitz with constant C. Similarly, if u = T x and v = T y are typical
vectors in V ,
kT
−1
u − T
−1
vk
2
= kT
−1
(T x) − T
−1
(T y)k
2
= kx − yk
2
≤
1
c
kT x − T yk =
1
c
ku − vk.
So T
−1
is Lipschitz with constant 1/c. It follows that both T and T
−1
are continu-
ous.
This means that if x
k
is a sequence of vectors in R
n
converging to a point x,
then T x
k
converges to T x because of the continuity of T . And conversely, if v
k
is a sequence of vectors in V converging to a vector v, then T
−1
v
k
converges to
T
−1
v in R
n
. This just says that there is a direct correspondence between conver-
gent sequences in R
n
and V . Since closed and compact sets are defined in terms
of convergent sequences, these sets correspond as well. Open sets are the comple-
ments of closed sets, so open sets correspond. If A ⊂ R
n
is bounded by L, the
Lipschitz condition shows that
kT ak = kT a − T 0k ≤ Ckak
2
≤ CL
for every a in A. So T (A) is bounded. Likewise, since T
−1
is Lipschitz, if B is a
subset of V bounded by L, it follows that T
−1
(B) is bounded by L/c in R
n
. ¥
Notice that we may conclude that closed and bounded sets also correspond.
Since the Heine–Borel Theorem shows that closed and bounded sets are compact
in R
n
, we can conclude that this is also true in all finite-dimensional normed spaces.
7.6.3. COROLLARY. A subset of a finite-dimensional normed vector space is
compact if and only if it is closed and bounded.
Another immediate consequence refers to the way a finite-dimensional sub-
space sits inside an arbitrary normed space. Arbitrary normed spaces are in general
not complete. However, finite-dimensional subspaces are, because we know the
Heine–Borel Theorem in R
n
.
7.6.4. COROLLARY. A finite-dimensional subspace of a normed vector space
is complete, and in particular it is closed.
PROOF. Let V be a normed vector space and let W be an n-dimensional subspace.
Let T be a linear invertible map from R
n
onto W as just constructed. Suppose that
7.6 Finite-Dimensional Normed Spaces 207
(w
k
)
∞
k=1
is a Cauchy sequence in W . Then since T
−1
is Lipschitz, the sequence
x
k
= T
−1
w
k
for k ≥ 1 is Cauchy in R
n
. (Check this yourself!) Since R
n
is
complete (Theorem 4.2.5), the sequence x
k
converges to a vector x. Again by
Corollary 7.6.2, we see that w
k
must converge to w = T x. Thus W is complete.
In particular, all of the limit points of W lie in W , so W is closed. ¥
As an application of these corollaries, we prove the following result, which is
fundamental to approximation theory.
7.6.5. THEOREM. Let (V, k·k) be a normed vector space, and let W be a finite
dimensional subspace of V . Then for any v ∈ V , there is at least one closest point
w
∗
∈ W so that kv − w
∗
k = inf{kv − wk : w ∈ W }.
PROOF. Notice that the zero vector is in W and so
inf{kv − wk : w ∈ W } ≤ kv − 0k = kvk.
Let M = kvk. If w satisfies kv − wk ≤ kvk, then
kwk ≤ kw − vk + kvk ≤ M + M = 2M.
Thus if we define K := {w ∈ W : kwk ≤ 2M}, then
inf{kv − wk : w ∈ K} = inf{kv − wk : w ∈ W }.
We will show that K is compact. Clearly K is bounded by 2M. The norm
function is Lipschitz, and hence continuous. Thus any convergent sequence of
vectors in K will converge to a vector of norm at most 2M. And since W is
complete, this limit also lies in W ; whence the limit lies in K. This shows that K
is closed and bounded. By our corollary, it follows that K is compact.
Now define a function on K by f (w) = kv − wk. This function has Lipschitz
constant 1 since
|f(w) − f(x)| =
¯
¯
kv − wk − kv − xk
¯
¯
≤ kw − xk.
In particular, f is continuous on the compact set K. By the Extreme Value Theorem
(Theorem 5.4.4), f achieves its minimum at some point w
∗
in K. This is a closest
point to v in W . ¥
Exercises for Section 7.6
A. Let V be a finite-dimensional vector space with two norms k · k and ||| · |||. Show that
there are constants 0 < a < A such that akvk ≤ |||v||| ≤ Akvk for all v ∈ V .
B. Let T be the invertible linear map from Corollary 7.6.2.
(a) Use the Lipschitz property of T and T
−1
to show that T (B
r
(x)) contains a ball
about T x in V ; and that T
−1
(B
r
(T x)) contains a ball about x in R
n
.
(b) Hence show directly that U is open if and only if T (U) is open.
C. Write out a careful proof of Corollary 7.6.3.
208 Normed Vector Spaces
D. Suppose that (w
k
)
∞
k=1
is a Cauchy sequence in a normed space W . If T : W → V is
a Lipschitz map into another normed space V , show that the sequence v
k
= T w
k
for
k ≥ 1 is Cauchy in V .
E. Show that for each integer n and each function f in C[a, b], there is a polynomial of
degree at most n that is closest to f in the max norm on C[a, b].
F. Let R
n
have the max norm kxk
∞
= max{|x
i
| : 1 ≤ i ≤ n}. Let K be the unit ball of
V and let v = (2, 0, . . . , 0). Find all closest points to v in K.
G. For strictly convex normed vector spaces (see Exercise 7.3.F), we have better approx-
imation results.
(a) Show that if W is a finite-dimensional subspace of a strictly convex normed vector
space V , then each point v ∈ V has a unique closest point in W .
(b) Show that R
n
with the standard Euclidean norm is strictly convex.
(c) Show that R
2
with the norm k(x, y)k
1
= |x| + |y| is not strictly convex.
(d) Find a subspace W of V = (R
2
, k · k
1
) so that every point in V that is not in W
has more than one closest point in W .
7.7. The L
p
norms
The L
p
norms on C[a, b] for 1 ≤ p < ∞ were defined in Example 7.1.5 by
kfk
p
=
µ
Z
b
a
|f(x)|
p
dx
¶
1/p
.
The point of this section is to prove that these really are norms by proving the trian-
gle inequality, which is the only part of the definition not established in Section 7.1.
There are other variants of the L
p
norms that are handled in exactly the same
way. Here are two important examples.
7.7.1. EXAMPLES. (1) For 1 ≤ p < ∞, `
p
consists of the set of all infinite
sequences a = (a
n
) such that
kak
p
=
³
∞
X
n=1
|a
n
|
p
´
1/p
< ∞.
It is again easy to see that this measure is positive definite and homogeneous.
We can deduce the triangle inequality from the main example by identifying
the sequence a with the function f on [0, ∞) given by
f(x) = a
n
for n − 1 ≤ x < n, n ≥ 1.
This function has the property that kfk
p
= kak
p
. So we can deduce our inequality
from the main case. You probably noticed that this function is not continuous.
However, if we prove the result for piecewise continuous functions, we shall be
able to apply the result here. (Alternatively, we could doctor this function so that
we still obtain the correct integral and the function is continuous. But this is not as
natural.)
7.7 The L
p
norms 209
(2) Let w(x) be a strictly positive piecewise continuous function on [a, b]. Then
define a norm on C[a, b] or even on the space P C[a, b] of piecewise continuous
functions by
kfk
L
p
(w)
=
µ
Z
b
a
|f(x)|
p
w(x) dx
¶
1/p
.
We call this the L
p
(w) norm. The standard case takes w(x) = 1. So if we prove
the result for L
p
(w), then it will follow for L
p
and for `
p
.
First we need an easy lemma from calculus.
7.7.2. LEMMA. Let A, B > 0. Then
A
t
B
1−t
≤ tA + (1 −t)B for all 0 < t < 1.
Moreover, equality holds for some (or all) t only if A = B.
PROOF. Since A > 0, write A = e
a
, where a = logA. Similarly, B = e
b
for
b = log B. Substituting these formulas for A and B, we have to prove that
e
ta
e
(1−t)b
= e
ta+(1−t)b
≤ te
a
+ (1 − t)e
b
.
But the preceding inequality follows from the convexity of the exponential function
on R (see Figure 7.4). As the exponential function is convex (apply Exercise 6.2.J),
we are done. ¥
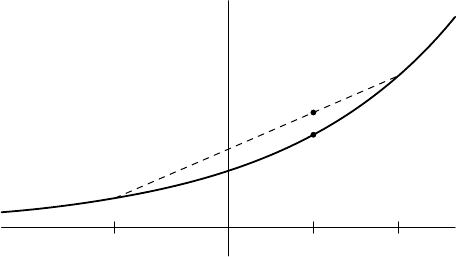
x
y
a
b
ta + (1 − t)b
te
a
+ (1 − t)e
b
exp(ta + (1 − t)b)
FIGURE 7.4. The convexity of e
x
.
We can now prove one of the most important inequalities of analysis, the
H
¨
older inequality.
210 Normed Vector Spaces
7.7.3. H
¨
OLDER’S INEQUALITY.
Let w be a positive function on an interval [a, b]. Let f ∈ L
p
(w) and g ∈ L
q
(w)
where 1 < p < ∞ and
1
p
+
1
q
= 1. Then
¯
¯
¯
¯
Z
b
a
f(x)g(x)w(x) dx
¯
¯
¯
¯
≤ kfk
L
p
(w)
kgk
L
q
(w)
.
PROOF. We may assume that f and g are nonzero because both sides are easily
seen to be 0 otherwise. Let
A =
|f(x)|
p
kfk
p
L
p
(w)
and B =
|g(x)|
q
kgk
q
L
q
(w)
.
Then take t = 1/p, so that 1 −t = 1/q, and apply the lemma. We obtain
|f(x)|
kfk
L
p
(w)
|g(x)|
kgk
L
q
(w)
= A
t
B
1−t
≤ tA + (1 −t)B
=
|f(x)|
p
pkfk
p
L
p
(w)
+
|g(x)|
q
qkgk
q
L
q
(w)
.
We now multiply by w(x) and integrate from a to b.
¯
¯
¯
¯
Z
b
a
f(x)g(x)
kfk
L
p
(w)
kgk
L
q
(w)
w(x) dx
¯
¯
¯
¯
≤
Z
b
a
|f(x)|
kfk
L
p
(w)
|g(x)|
kgk
L
q
(w)
w(x) dx
≤
1
p
Z
b
a
|f(x)|
p
kfk
p
L
p
(w)
w(x) dx +
1
q
Z
b
a
|g(x)|
q
kgk
q
L
q
(w)
w(x) dx
=
1
p
+
1
q
= 1
Multiplying by kfk
p
L
p
(w)
kgk
q
L
q
(w)
gives the inequality. ¥
7.7.4. EXAMPLES.
(1)
Z
b
a
f(x)g(x) dx ≤
µ
Z
b
a
f(x)
p
dx
¶
1/p
µ
Z
b
a
g(x)
q
dx
¶
1/q
for all continuous functions f and g on [a, b]. This is just the standard weight
w(x) = 1.
(2) If we take p = 2, then q = 2 and we obtain the Cauchy–Schwarz inequality,
Theorem 7.3.4, for L
2
(w).

7.7 The L
p
norms 211
(3) As in Example 7.7.1(1), take w(x) = 1 on [0, ∞) and consider f(x) = a
n
and
g(x) = b
n
on [n − 1, n] for n ≥ 1, where (a
n
) ∈ `
p
and (b
n
) ∈ `
q
. Then
∞
X
n=1
a
n
b
n
=
Z
∞
0
f(x)g(x) dx ≤
µ
Z
b
a
f(x)
p
dx
¶
1/p
µ
Z
b
a
g(x)
q
dx
¶
1/q
=
³
∞
X
n=1
|a
n
|
p
´
1/p
³
∞
X
n=1
|b
n
|
q
´
1/q
.
Again, this reduces to the Cauchy–Schwarz inequality if p = q = 2.
The triangle inequality now follows by another trick.
7.7.5. MINKOWSKI’S INEQUALITY.
The triangle inequality holds for L
p
(w), that is,
³
R
b
a
|f(x) + g(x)|
p
w(x)dx
´
1/p
≤
³
R
b
a
|f(x)|
p
w(x)dx
´
1/p
+
³
R
b
a
|g(x)|
p
w(x)dx
´
1/p
.
PROOF. Notice that
1
q
= 1 −
1
p
=
p − 1
p
. So q =
p
p − 1
. Thus
k|f|
p−1
k
L
q
(w)
=
µ
Z
b
a
|f(x)|
(p−1)q
w(x) dx
¶
1/q
=
µ
Z
b
a
|f(x)|
p
w(x) dx
¶
1/q
= kf k
p/q
L
p
(w)
= kf k
p−1
L
p
(w)
.
We use this equality in the last line of the next calculation, which estimates the
norm of f + g in L
p
(w),
kf + gk
p
L
p
(w)
=
Z
b
a
|f(x) + g(x)|
p−1
|f(x) + g(x)|w(x) dx
≤
Z
b
a
|f(x)+g(x)|
p−1
|f(x)|w(x) dx
+
Z
b
a
|f(x)+g(x)|
p−1
|g(x)|w(x) dx
≤ k|f + g|
p−1
k
L
q
(w)
¡
kfk
L
p
(w)
+ kgk
L
p
(w)
¢
= kf + gk
p−1
L
p
(w)
¡
kfk
L
p
(w)
+ kgk
L
p
(w)
¢
.
Now divide by kf + gk
p−1
L
p
(w)
to obtain
kf + gk
L
p
(w)
≤ kfk
L
p
(w)
+ kgk
L
p
(w)
.
¥
212 Normed Vector Spaces
Exercises for Section 7.7
A. Rework the H
¨
older inequality to show: If a
n
≥ 0 and b
n
≥ 0 and 0 < t < 1, then
∞
X
n=1
a
t
n
b
1−t
n
≤
µ
∞
X
n=1
a
n
¶
t
µ
∞
X
n=1
b
n
¶
1−t
.
B. Show that the H
¨
older inequality is sharp in the sense that for every f ∈ L
p
(w), there
is a nonzero g ∈ L
q
(w) so that
¯
¯
¯
Z
b
a
f(x)g(x)w(x) dx
¯
¯
¯
= kfk
L
p
(w)
kgk
L
q
(w)
.
HINT: For nonzero f, set g(x) = |f(x)|
p
/f(x) if f(x) 6= 0 and g(x) = 0 if f(x) = 0.
C. Let f(t) be a continuous, strictly increasing function on [0, ∞) with f(0) = 0. Recall
that f has an inverse function g with the same properties by Theorem 5.7.6. Define
F (x) =
Z
x
0
f(t) dt and G(x) =
Z
x
0
g(t) dt.
(a) Prove Young’s Inequality: xy ≤ F (x) + G(y) for all x, y ≥ 0, with equality if
and only if f(x) = y.
HINT: Sketch f and find two regions with areas F (x) and G(y).
(b) Take f(x) = x
p−1
for 1 < p < ∞. What inequality do you get?
D. Let f
n
= n
χ
[
1
n
,
2
n
]
be defined on [0, 1] for n ≥ 2.
(a) Show that f
n
converges pointwise to 0.
(b) Show that f
n
does not converge in L
p
[0, 1] for any 1 ≤ p < ∞.
E. (a) If f ∈ C[0, 1] and 1 ≤ r ≤ s < ∞, show that kfk
1
≤ kfk
r
≤ kfk
s
≤ kfk
∞
.
HINT: Let p =
s
r
and think of
Z
1
0
|f|
r
· 1dx as the product of an L
p
function and
an L
q
function.
(b) Hence show that if f
n
∈ C[0, 1] converge uniformly to f, then they also converge
in the L
p
norm for all 1 ≤ p < ∞.
F. Let f
n
=
1
n
χ
[0,n
n
]
be defined on [0, ∞) for n ≥ 1.
(a) Show that f
n
converges uniformly to 0.
(b) Show that f
n
does not converge in L
p
[0, 1] for any 1 ≤ p < ∞.
G. (a) If a = (a
k
) ∈ `
1
and 1 ≤ r ≤ s < ∞, show that kak
∞
≤ kak
s
≤ kak
r
≤ kak
1
.
HINT: Show that for p ≥ 1,
n
P
k=1
|b
k
|
p
≤
³
n
P
k=1
|b
k
|
´
p
.
(b) Hence show that `
1
⊂ `
r
⊂ `
s
⊂ `
∞
.
H. Find continuous functions f and g on [0, ∞) so that f is in L
1
[0, ∞) but not in
L
2
[0, ∞), and g is in L
2
[0, ∞) but not in L
1
[0, ∞).
